Методичні рекомендації щодо проведення сучасного уроку математики в початковій школі.

Про матеріал

Корисне і цікаве на уроках математики.Творча робота над задачею, математичні диктанти, диференційовані завдання, задачі з геометричним матеріалом та з елементами дослідження, задачі з логічним навантаженням.

Перегляд файлу

Відділ освіти і науки Нікопольської міської ради

Комунальний заклад «Нікопольська середня загальноосвітня школа І-ІІІ ступенів №21»

Методичні рекомендації щодо проведення сучасного уроку математики в початковій школі

Вчитель початкових класів

Медведєва Наталя Олександрівна

Сучасний урок математики в початковій школі

Сучасний урок - це актуальний урок, це основний механізм засвоєння школярами стандартів освіти та формування

рівня , що перевищує ці стандарти.

На уроці в першу чергу формуються компетентності дитини ,що представляють собою одну з головних ідей

модернізації.

Саме урок є важливою формою індивідуального підходу до дитини,урахування її інтересів і здатностей

розвитку особистісних якостей, необхідних для життя в сучасному суспільстві.

Сучасний урок повинен бути пов’язаний не тільки із засвоєнням школярами певної суми знань,а й цілісним

розвитком особистості ,її пізнавальних і творчих здатностей.

Вчителі залучають учнів до активного одержання знань ,складання схем, до творчої діяльності.

Усі учні стають учителями,а клас-діяльною громадою тих ,хто вчиться.

Учні перетворюються на особистостей здатних упродовж всього життя відкривати нові ідеї

та інформацію і трансформувати її у практичні вміння і навички.

Завдання кожного педагога-дійти до серця кожного учня ,відчути кожному себе особистістю,

створити умови для легкого , доступного ,якісного засвоєння програмового матеріалу.

«Доклади серця свого до навчання і вуха свої до розумних слів…»

Притча Соломона

Корисне і цікаве на уроках математики

Чим цікавіше для дитини те, що вона вивчає, тим більше зосереджується її увага, тим глибше засвоюються знання.

В. Сухомлинський

Зацікавити учнів математикою, показати її могутність і красу, допомогти полюбити її — завдання кожного вчителя.

Проте часто доводиться чути від учнів, що математика — важкий предмет. Можна навіть простежити, як змінюється їхнє ставлення до цього предмета в процесі навчання. У 1-му класі уроки математики проводяться в ігровій формі, а швидка зміна різних видів діяльності учнів та унаочнення дає можливість урізноманітнювати заняття, запобігати перевтомі дітей.

Але проходить час, і яскраві наочні посібники замінюють сухі умовні схеми, а згодом і їх стає менше. Інакше й бути не може, бо цього вимагає високий рівень абстрактності самої математики. Тим часом завдання ускладнюються, кожне з них потребує дедалі більше часу і зусиль. Урок математики стає буденною роботою. Але дітям ще далеко до того, щоб любити математику заради неї самої.

Стикаючись із першими труднощами, діти перестають розуміти матеріал. Головна причина — невміння розв'язувати текстові задачі. У маленьких школярів не , розвивається логічне мислення, а із цього виростають усі майбутні невдачі, а також зневіра дітей у своїй здатності добре знати математику.

Щоб цього не сталося, треба активізувати розумову діяльність учнів.

Розумові здібності дитини потребують постійного вправляння, так само, як розвиток навичок читання, обчислення, письма тощо.

На кожному уроці необхідно знайти кілька хвилин, щоб повправляти розум дітей, посприяти розвитку гнучкості й швидкості розумових процесів. Маю на увазі, зокрема, короткочасні завдання, що стимулюють швидке напружене міркування. Завдяки таким вправам пожвавлюється урок, у дітей виробляється смак до напруженої розумової роботи.

Розумова розминка

Гра «Не скажу»

Полічити до 70, говорячи замість чисел, які діляться на 7, слово «не скажу». Виграє той, хто не зіб’ється.

Числова драбина

Щоб піднятися на сходинку цієї числової драбинки, треба додати 23, а щоб спуститися – відняти 12. Пройдіть драбину до кінця.

+23
		134		147		158		169
	111		124		135		146
-12

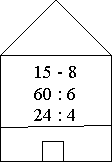
Гра «Лабіринт»

Двері будиночка відкриває тільки число 6.

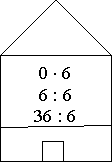
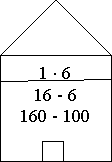
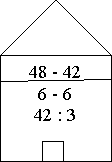
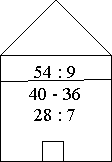
Гра «Нанизай намистинку»

Задачі з логічним навантаженням

Используя цифры 0, 1,3,5, запиши наибольшее и наименьшее пятизначное числа.
Сумма двух чисел равняется 157. Одно из чисел заканчивается цифрой 3. Если эту цифру зачеркнуть, то получится второе число. Напиши эти числа.

143 – 143 + 14 = 157

Сколькими способами можно переставить цифры в числі 9874?

9784	8794	7498	4987
9847	8749	7849	4897
9478	8479	7489	4789
9487	8497	7948	4798

К неизвестному числу прибавим 1200. После этого оно увеличилось в 26 раз. Найти неизвестное. (3000)
Запиши два пятизначні числа, сумма цифр в каждом из которых равняется 9 . Найти разность этих чисел.
Из каждых 100кг свежих фруктов получается 18 кг сушёных. Сколько килограммов сушёных фруктов получат из 900 кг свежих?

При розв’язуванні задач з логічним навантаженням діти відзначаються наполегливістю, уважністю, з’ясовують оригінальні та цікаві прийоми, проявляють ініціативу. Створюється творча атмосфера, діти вірять в свої сили, не комплексують через окремі невдачі, радіють за однокласників.

Фрагменти роботи над задачами

Задача № 1

Як можна поставити в шеренгу Настю (Н), Тетяну (Т), Михайла (М), та Сергія (С), щоб хлопчики (х) і дівчата (д) чергувались?

а) Використовуючи умовні позначення імен дітей, записати різні варіанти розположення дітей в шеренгу, які відповідають даній умові:

Спосіб перебору можна замінити схемою, яку називають деревом різних варіантів:

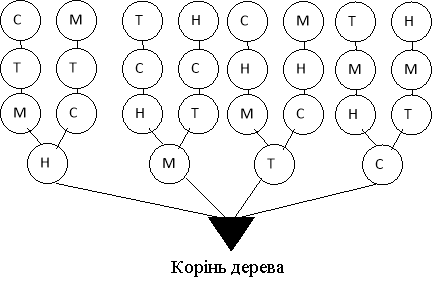
Четвертий

Третій

Другий

Перший

Схему-дерево можна зробити різними варіантами.

Завдання 1.

Розмістити схему-дерево, якщо корінь дерева знаходиться вгорі.

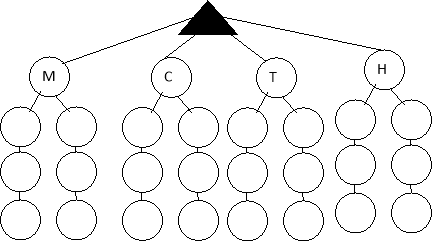
Четвертий

Третій

Другий

Перший

Завдання 2.

Обвести червоним кольором гілочки на схемі 2, які відповідають:

б)

в)

а)

Завдання 3.

Обвести синім кольором кілочки на схемі 2, які відповідають:

а)

б)

Цікаві задачі.

Для активізації розумової діяльності учнів дуже корисні розважальні задачі. Вони викликають веселе пожвавлення в класі та світять вогник цікавості в очах дітей. На кожному уроці необхідно створювати позитивний емоційний фон, настрій, який полегшує сприймання будь-якого матеріалу.

М. Беренко «Позичайло Джафар»

Задача 1.

Хто позичає гроші у Джафара, зобов’язаний повернути йому всю суму та ще її п’яту частину. Юсуп взяв у Джафара 5245 монет. Скільки монет він зобов’язаний повернути?

Задача 2.

Джафар переносить 259460 монет у надійне місце. Він зробив 6 ходок, переносячи 2846 монет за один раз. Скільки монет йому залишилось перенести?

Задача 3.

Джафар пригнав свій караван в Україну, а тут на верблюдах не їздять. Довелося передати 11 верблюдів у зоопарк за чверть їх ціни. Скільки грошей отримав Джафар, якщо раніше заплатив за кожного верблюда 412 монет?

Задачі з казковим сюжетом

Казка для молодших школярів – не просто оповідання про фантастичні події, це цілий світ, в якому дитина живе, змагається, протиставляє злу свою добру волю.

Перше ознайомлення з першою казкою – велика подія у житті дитини. Її симпатії завжди на боці позитивних героїв. Добро перемагає, а зло карається. Через задачі казки продовжують виховувати.

Задача 1.

Карлсон зможе з’їсти 90 бубликів за 10 днів, а Фрекен Бок – за 15. За скільки днів з’їдять цю кількість бубликів Карлсон і Фрекен Бок, якщо будуть їсти разом?

Задача 2.

Кажуть, що черепаха Тортіла віддала золотий ключик Буратіно не так просто, як розповів письменник О. Толстой. Вона винесла три коробочки: червону, синю та зелену. На червоній коробочці було написано: «Тут лежить золотий ключик»; на синій – «Зелена коробочка порожня» а на зеленій – «Тут сидить змія».

Тортіла прочитала напис і сказала: «Дійсно, в одній коробочці лежить золотий ключик, у другій – змія, а третя – порожня, але всі написи неправильні. Якщо відгадаєш, в якій коробочці лежить золотий ключик, він – твій».

Де лежить золотий ключик?

Міркування: Із напису на синій коробці можна здогадатися, що в зеленій коробці щось знаходиться. Це не змія, тому що напис на зеленій коробці неправильний. Отже, золотий ключик у зеленій коробці.

Задачі з геометричним матеріалом та з елементами дослідження.

Завдання геометричного змісту розвивають просторові уявлення, увагу, спостережливість, нестандартність у виконанні завдань, пам’ять. Потрібна наполеглива і цілеспрямована робота.

Завдання 1.

Викласти з паличок таку фігуру. Прибрати 6 паличок, щоб зосталось три квадрати. Намалювати два варіанта рішення.

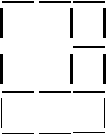
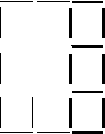
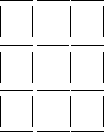
Завдання 2.

Записати назви всіх многокутників, які не мають кути АВС.

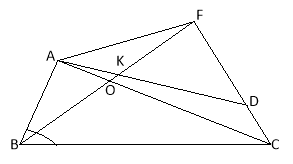
Завдання 3.

Записати, скільки відрізків на малюнку.

Завдання 4.

Поділити фігуру серпа місяця на 6 частин, провівши 2 прямі.

Завдання 5.

Це – магічна зірка. Сума чотирьох чисел на кожному відрізку зірки рівна 26. Знайти ці числа.

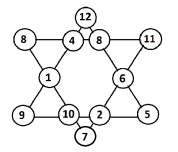
Розв’язок:

26 – (1+4+12) = 9
26 – (1+10+7) = 8
26 – (8+4+3) = 11
26 – (7+2+11) = 6
26 – (12+3+ 6) = 5

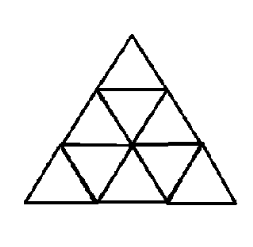
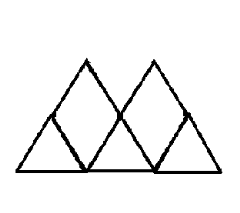
Завдання 6.

Із паличок побудувати фігуру. Прибрати 5 паличок так, щоб зосталось 5 трикутників.

Математичні диктанти.

Корисні для розвитку математичного мовлення й мислення різноманітні математичні диктанти, які часто практикую у своїй роботі.

Робота над картками.

Знайти помилку та виправити її.

36  2 = 72	100 – 19  2 = 138 62
23  4 = 87 92	(820 - 800)  8 = 160
96 : 8 = 12	64 + 20  5 = 164
26  3 = 66 78	200 – 40  2 = 320 120
12  8 = 82	17 – 68 : 4 = 0

Обчислити приклади й потім розшифрувати слово.

124	236	151	202
4	2	3	4
С	В	Ь	Е

247	308	107	136
2	2	4	5
Е	Р	Н	Е

472	494	616	808	496	680	428	453

Слово: ВЕРЕСЕНЬ

Гра-естафета «Цікавинка»

350 + 180 =	870 – 480 =	680 + 270 =
- 90 =	+ 50 =	- 190 =
+ 260 =	+ 560 =	– 80 =
- 25 =	- 170 =	+ 320 =
+ 360 =	– 40 =	– 660 =
+ 520 =	+ 130 =	+ 570 =
Учні 1-го ряду	Учні 2-го ряду	Учні 3-го ряду

Гра «Комп’ютер»

96	:				48	:	:	13

	12	*			-	3		+	18

	-	84	5	*				24	*

	7			30	+				72

					39

Творча робота над задачею

Важливо подбати про те, щоб кожний учень активно із захопленням працював на уроці. Формування пізнавального інтересу до вивчення математики ґрунтується саме на тому, що учень відчуває свою здатність до сприйняття та застосування знань, умінь та навичок, набутих при вивченні математики.

Розв’язанню цієї проблеми сприятиме використання нових ефективних методичних прийомів, які активізували б мислення школярів, стимулювали б їх до самостійного набуття знань.

Поступове ускладнення умови текстової задач дає можливість кожному, навіть найслабшому, учневі включитись в роботу. Зрозумівши, як розв’язувати найпростішу задачу, що лежить в основі всіх наступних, учні запам’ятовують, як починати розв’язувати задачу, а далі змушені шукати та встановлювати залежності між новими даними, що з’явились в задачі.

Ускладнені задач сприяють формуванню в школярів уміння уявити зміст задачі, оперувати з величинами, які перебувають у взаємозв’язаних математичних відношеннях, утримувати їх у пам’яті та знаходити раціональний шлях розв’язання. Всі задач виконуються арифметичними способами, але вибір дій здійснюється на основі логічного аналізу умови, який передбачає обґрунтоване та аргументоване виявлення існуючих зв’язків між величинами.

Варіанти поступового ускладнення задачі

Варіант 1

№ 1

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого – 20. Скільки борошна залишилось у мішку?

№ 2

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого – в 2 рази менше. Скільки борошна залишилось у мішку?

№ 3

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого – 1/2 того, що було спочатку. На скільки більше взяли борошна першого разу, ніж другого?

№4

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого — 1/2 того, що було спочатку. На скільки більше борошна взяли другого разу, ніж залишилось?

№ 5

У мішку було 52 кг борошна. Першого разу з нього взяли 1/4 всієї кількості, другого — 1/2 всього борошна. Скільки борошна залишилось у мішку?

№ 6

У мішку було 52 кг борошна. Першого разу з нього взяли 1/4 всієї кількості, другого — 1/3 решти. Скільки борошна залишилось у мішку?

№ 7

У мішку було 52 кг борошна. Першого разу з нього взяли. 1/4 всієї кількості, другого — 1/3 решти. На скільки більше борошна взяли, ніж залишилось у мішку?

№ 8

У мішку було 52 кг борошна. Першого разу з нього взяли 1/4 всієї кількості, другого — 1/2 всього борошна, а решту розсипали в пакети по 3 кг в кожний. Скільки всього зайняли пакетів?

№ 9

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, це в 2 рази менше, ніж другого разу. На скільки більше борошна взяли, ніж залишилось у мішку?

№ 10

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого — половину решти. Борошно, що забрали, розсипали в пакети по 4 кг в кожний. Скільки отримали пакетів з борошном?

№ 11

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого — п'яту частину решти. Борошно, що забрали, розсипали в пакети по 4 кг в кожний. На скільки пакетів з борошном більше отримали першого разу, ніж другого?

№ 12

У мішку було 52 кг борошна. Першого разу з нього взяли 12 кг, другого — п'яту частину решти, а 1/4 того, що залишилось розсипали в пакети по 4 кг в кожний. Скільки заповнили пакетів?

№ 13

У мішку було 52 кг борошна. Першого разу з нього взяли половину борошна, другого — 1/2 половини. У скільки разів більше взяли, ніж залишилося?

Варіант 2

№ 1

Туристи мали пройти 180 км. Після того як вони пройшли частину шляху, їм залишилось пройти 48 км. Скільки кілометрів пройшли туристи?

№ 2

Туристи мали пройти 180 км. Після того як вони пройшли частину шляху, їм залишилось пройти 48 км. На скільки кілометрів туристи пройшли більше, ніж залишилось?

№ 3

Туристи мали пройти 180 км. Після того як вони пройшли третину маршруту, половину решти шляху, вони проїхали на автобусі. На скільки кілометрів туристи пройшли більше, ніж проїхали?

№4

Туристи мали пройти 180 км. Першого дня вони пройшли половину шляху,а другого — на 35 км більше. Скільки кілометрів залишилось пройти туристам?

№ 5

Туристи мали пройти 180 км. Першого дня вони подолали третину шляху, а другого — пройшли 2 дороги по 30 км. Скільки кілометрів залишилось пройти туристам?

№6

Туристи мали пройти 180 км. Пішки вони пройшли п'яту частину шляху, човнами — шосту частину шляху.На скільки кілометрів більше туристи подолали, ніж їм залишилось?

№ 7

Туристи мали пройти 180 км. Три дні вони йшли по 20 км, два дні — по 35 км, а решту вирішили пройти за 2 дні. По скільки кілометрів за день проходили туристи решту шляху?

№8

Туристи мали пройти 180 км. Три дні вони проходили по 20 км, два Дні — по 15 км, а решту йшли по 30 км за день. За скільки днів туристи подолали весь шлях?

№ 9

Туристи мали пройти 180 км. Першого дня вони подолали третину шляху, Це в 2 рази менше, ніж другого дня. Скільки кілометрів залишилося пройти туристам?

№ 10

Туристи мали пройти 180 км. Коли вони подолали 1/3 частину шляху, їм залишилось ще частина, яка

в 2 рази більше, ніж вони пройшли спочатку. Яку частину шляху залишилося подолати?

Творча робота над задачами

У методичній літературі творчу робота над задачами пропонується використовувати з різною метою: для розвитку творчості учнів; формування уявлень учнів про структуру задачі, про механізм розв’язування задачі, формування в учнів уміння розв’язувати задачі певного виду; узагальнення і усвідомлення зв’язків між величинами; засвоєння дітьми арифметичних дій та їх властивостей; диференціації навчання; моделювання конкретної життєвої ситуації математичною мовою.

Залежно від мети вчитель вибирає той чи інший вид творчої роботи над задачами. Це обумовлює необхідність систематизації видів такої роботи. Всі види творчої роботи над задачами поділяються на дві групи:

творча робота над задачами певного типу;
творча робота над конкретною задачею.

Зупинімося детально на завданнях кожної групи.

1. ТВОРЧА РОБОТА НАД ЗАДАЧАМИ ПЕВНОГО ТИПУ

Робота з невизначеними та переозначеними задачами.

Якщо задача має єдиний розв’язок, то вона називається визначеною. Якщо ж у задачі кількість вказівок на залежності між величинами або числовими даними недостатня, то вона може мати багато розв’язків і називається невизначеною. Якщо є зайві вказівки або числові дані, то задачу називають переозначеною.

Робота над невизначеними та переозначеними задачами сприяє розвитку уявлень учнів про структуру задачі, підготовці до розв’язування складених задач, формуванню звички до глибокого аналізу зв’язків між даними і шуканими, розуміння зв’язку навчання із життям, бо розв’язуючи задачі з недостатніми даними, учні згадують необхідні числа або зв’язки із власного досвіду, підбирають необхідні дані з довідкових таблиць.

Доповнення неповної задачі необхідними числовими даними.

Задача. У двох клітках було 18 кролів. Скільки кролів було у другій клітці?

Після ознайомлення із задачею учні розуміють, що вона не має єдиного розв’язку. Щоб задача мала єдиний розв’язок, можна вказати, скільки кролів було в першій клітці (або що в обох клітках було кролів порівну).

Запропонувавши учням доповнити задачу вказівками «у другій клітці було на 2 кролі більше (менше)» або «у другій клітці було в два рази більше (менше) кролів», одержимо задачу підвищеної складності.

Доповнення неповної задачі необхідними зв’язками.

Учні повинні розуміти, що умова і запитання в задачі логічно пов’язані.

Задача. Хлопчик, дівчинка і їхня бабуся збирали гриби. Хлопчик знайшов 5 білих грибів, а дівчинка на 2 гриби більше. Скільки білих грибів зібрала бабуся?

Учні говорять, що задачу розв’язати неможливо, бо про кількість грибів, які зібрала бабуся, в умові нічого не сказано.

Учитель пропонує учням кілька запитань:

Чи є число, що відповідає запитанню задачі?
Чи могла бабуся зібрати 0 білих грибів?
Чи могла бабуся зібрати стільки ж грибів, як і дівчинка?
Доповніть задачу такою вказівкою і сформулюйте одержану задачу.
Як її розв’язати? (Розв’язання запишіть на дошці.)
Як іще можна доповнити умову задачі, щоб вона мала розв’язок?

Доповнивши задачу вказівками «бабуся зібрала на 3 гриби більше (менше), ніж хлопчик» та «бабуся зібрала стільки, скільки хлопчик і дівчинка разом», одержують ще 2-3 задачі, розв’язання яких записують на дошці.

Узагальнюючи проведену роботу, доцільно наголосити: для розв’язування задачі необхідно знати, які зв’язки існують між даними і шуканими числами.

Задача. На двох ділянках прямокутної форми посаджена картопля. Довжина першої ділянки 40 м, а ширина 30 м. Яка довжина другої ділянки, ширина якої 20 м?

У даній задачі учні можуть не побачити, що між розмірами ділянок немає жодного зв’язку, вважаючи, що площі ділянок рівні. Учитель пропонує зачитати, де сказано, що площі рівні. Цих відомостей учні не знаходять і говорять, що задачу розв’язати не можна.

Доповнивши умову задачі вказівками «площі ділянок однакові», «площа першої ділянки на 120 м² більша (менша) від площі другої ділянки» та записавши розв’язання одержаних задач на дошці, учні доходять висновку: при аналізі задач варто звертати увагу на наявність зв’язків між частинами умови та між умовою і запитанням.

Розв’язування задач із зайвими даними.

Уміння розв’язувати задачі із зайвими даними — одна з умов успішного розв’язування багатьох складених задач, правильного розуміння структури задач. Цінність таких задач полягає в їх практичній спрямованості, бо в повсякденній діяльності доводиться вибирати із сукупності чисел необхідні дані. Ці задачі корисні й для розвитку критичності мислення.

Задачі із зайвими даними можна поділити на три різновиди:

1. Задачі, в яких зайві числа не є даними задачі, а слугують лише для повноти фабули.

Задача. Влітку 2 учні збирали лікарські рослини. Один зібрав 12 кг, а другий на 3 кг менше. Скільки кілограмів лікарських рослин зібрали ці учні?

Робота з такими задачами здебільшого проводиться на основі аналізу помилок, допущених учнями.

Задачі, в яких зайві дані не охоплюються запитаннями. Вони зайві для одержання відповіді на поставлене запитання, але можуть виявитись необхідними у разі зміни запитання або спроби розв’язати задачу іншим способом. До цих задач відносимо задачі, складені на основі табличних даних, і задачі з двома запитаннями. В умові задач із двома запитаннями можуть бути:

чотири числа, які можна об’єднати тільки певними парами.

Задача. У групі дитячого садка було 5 відерець і 4 лійки. Купили ще 3 відерця і 2 лійки. Скільки стало відерець? Скільки стало лійок?

Б) три числа, одне з яких (і лише одне) поєднується з двома іншими.

Задача. За столом у їдальні сідають обідати 6 осіб. На стіл поклали 4 ложки і 3 виделки. Скільки ложок іще треба покласти? Скільки виделок?

три числа, кожні два з яких можна поєднати в пари.

Задача. Діти посадили 7 лип, 5 дубів і 8 беріз. Скільки всього дубів і лип посадили?

У задачах із двома запитаннями можуть поєднуватись не лише прості задачі, а й складена з простою.

Задача. Ящик із печивом важить 12 кг і коштує 180 грн., а ящик з виноградом важить на 4 кг менше і коштує 120 грн. Яка ціна 1 кг печива? Яка ціна 1 кг винограду?

Задачі, в яких зайві дані переозначують їх умови.

В цьому випадку числові дані можуть бути несуперечливими (задача не має єдиного розв’язку).

Задачі з несуперечливими даними третьої групи показують учням можливості знаходження розв’язку різними шляхами.

Задача. В понеділок у бібліотеці побували 75 читачів, у вівторок — на 35 читачів менше, ніж у понеділок, а в середу — 50 читачів, на 25 читачів менше, ніж у понеділок. Скільки всього читачів відвідали бібліотеку за ці 3 дні?

До зайвих даних може бути віднесене кожне з трьох чисел: 75, 50 або 25.

Якщо зайвим вважати число 75, то розв’язання буде:

50 + 25 = 75 (ч.);
75 - 35 = 40 (ч.);
75 + 40 + 50 = 165 (ч.).

Якщо зайвим вважати число 50, то розв’язання матиме вигляд:

75 - 35 = 40 (ч.);
75 - 25 = 50 (ч.);
75 + 40 + 50 = 165 (ч.).

Якщо зайвим вважати число 25, то отримаємо розв’язання:

75 - 35 = 40 (ч.);
75 + 40 + 50 = 165 (ч.).

Учні бачать, що до знаходження розв’язку можна підійти різними шляхами, використовуючи різні числові дані й зв’язки між ними, які не суперечать одне одному.

Задача. У трьох сувоях залишилось 19 м тканини. У першому — 4 м, у другому — на 3 м більше, а у третьому на 2 м більше, ніж у другому. Скільки метрів тканини залишилось у третьому сувої?

Розв’язуючи задачу відповідно до послідовності розгортання її умови, маємо:

4 + 3 = 7 (м) — у другому сувої;
7 + 2 = 9 (м) — у третьому сувої.

Перевіряємо розв’язок:

4 + 7 + 9 = 20 (м) — у трьох сувоях.

В умові сказано, що всього залишилось 19 м. Отже, в умові є суперечливі дані. Якщо вилучимо вказівку «у третьому на 2 м більше», то матимемо розв’язання:

4 + 3 = 7 (м);
4 + 7 = 11 (м);
19 - 11 = 8 (м).

Порівнюючи різні розв’язання, учні бачать, що в переозначених задачах зайві дані можуть бути суперечливими, і задача не матиме єдиного розв’язку. Розв’язанням таких задач є доведення, що задача не має єдиного розв’язку.

Наведені зразки задач з недостатніми і зайвими даними показують, що вчитель може звичайну задачу підручника математики зробити невизначеною, визначивши одне з числових даних, або переозначеною, ввівши зайві дані.

1.2. Самостійне складання задач учнями.

Завдання на самостійне складання задач ефективні для розвитку уявлень учнів про структуру задачі, для усвідомлення ними способів розв’язування задач певного виду, розуміння залежностей між величинами.

Складання задач на основі спостережень за предметами, що оточують дітей, та їхніх практичних дій.

Після ознайомлення учнів із задачею та її елементами доцільно запропонувати їм складати задачі на основі власних дій та спостережень за навколишніми предметами.

Учитель пропонує одному з учнів покласти в кошик З яблука та 2 груші і дає всім учням завдання скласти на основі цих дій задачу. Доцільно наголосити, що задачі зустрічаються на кожному кроці. Для цього вчитель підходить, наприклад, до парти і говорить, що на парті також є задача: «На парті лежать 2 книги і 4 зошити. Скільки разом книг і зошитів на парті?»

Далі вчитель пропонує скласти задачі про предмети, які є в класі. Доцільно такі завдання давати і на прогулянках.

Складання задач на вказані дії.

Здебільшого учням пропонується скласти задачу на одну дію. Наприклад, скласти задачу, яка б розв’язувалась дією віднімання.

Вимога скласти задачу спонукає учнів до відшукування тих задачних ситуацій, які реалізуються вказаною дією; сприяє з’ясуванню області застосування арифметичних дій.

Можна запропонувати скласти задачу на дві дії. Наприклад, скласти задачу, яка б розв’язувалась діями додавання і ділення. Це сприятиме закріпленню уявлень учнів про структуру задач та формуванню навичок розв’язування задач певних типів.

Доцільно, формулюючи такі завдання, спиратися на схеми розв’язання. Наприклад, скласти задачу на віднімання і ділення, користуючись схемою:

(□-□):□

Вид задачі може визначатися зміною величин чи залежностями між величинами. Подамо зразки постановки завдань у цьому випадку:

Скласти задачу на знаходження вартості.
Скласти задачу на зменшення числа в кілька разів (на кілька одиниць).

Скласти задачу про швидкість, час і відстань.
Скласти задачу про норми витрати продуктів, про урожайність, продуктивність праці тощо.

Можна також пропонувати учням складати задачі із заданими словами. Наприклад: скласти дві задачі зі словом «виїхали», щоб одна розв’язувалась дією додавання, а інша — віднімання.

Складання задач за розв’язанням.

Якщо розв’язання записане виразом, то його спочатку слід проаналізувати колективно, визначивши порядок дій та з’ясувавши, які прості задачі можуть розв’язуватись такими діями.

Спочатку для таких завдань пропонуємо вирази на одну дію. Ефективність роботи підвищиться, якщо використовувати ситуації дидактичних ускладнень. Наприклад: скласти дві задачі — одну за виразом 4 + 2, а іншу за виразом 4 — 2; у кожній вжити слово «полетіли».

Складанням задач за виразами варто охопити основні види задач на дві, а то й на три дії.

Часто вчитель сам пропонує певний сюжет, а потім учні знаходять і інші сюжети для даного виразу. Наприклад, учитель пропонує скласти задачу на рух за виразом 5 • 3 + +60 • 2. Потім учні разом міркують над тим, про що іще можна скласти задачу за цим виразом.

Складаючи задачу за розв’язанням окремими діями, слід з’ясувати, що задані дві дії можуть входити у розв’язання складеної задачі, якщо результат першої дії є компонентом другої. Наприклад, дії:

1)28 : 7 = 4; 2) 54 + 7 = 61 не можуть бути розв’язанням складеної задачі на дві дії, а дії: 1) 56 : 7 = 8; 2) 8 • 5 = 40 можуть бути розв’язанням, наприклад, задачі на зведення до одиниці.

Складання задач певного виду.

За допомогою таких завдань формуються вміння розв’язувати задачі певного виду. їх застосовують у двох випадках: коли потрібно 1) скласти аналогічну задачу до поданої або 2) скласти задачу вказаного виду. У першому випадку завдання зводиться до заміни числових даних або зміни сюжету. Наведемо зразки завдань другого виду:

Скласти задачу на знаходження невідомого від’ємника.
Скласти задачу на знаходження суми двох добутків (двох часток).
Скласти задачу на знаходження відстані при зустрічному русі.
Розв’язати задачу на знаходження невідомого за двома різницями, а потім перетворити її на задачу на пропорційне ділення.

Складання задач за числовими даними.

Для подання числових даних бажано використовувати рисунки, на яких зображені предмети з числовими характеристиками. Ефективність роботи зростає, якщо подаються не ізольовані пари предметів, а сукупності кількох предметів. Такими таблицями можуть бути зображення шкільних предметів, біля яких написані їх ціни; зображення тварин і їхні маси; зображення засобів руху і їх швидкості; таблиці з нормами висіву рослин; таблиці з відомостями про урожайність сільськогосподарських культур тощо.

Матеріали таблиць опрацьовуються усно або у вигляді математичного диктанту. За такими таблицями учні активно складають не лише прості, а й складені задачі.

1.2.6. Складання обернених задач.

Складання обернених задач сприяє розкриттю структури задачі, усвідомленню взаємозв’язків між задачами, способів розв’язування та перевірки розв’язку.

Взаємооберненими називають задачі з одними і тими самими величинами, їх значеннями та зв’язками між ними, коли те, про що запитується в першій задачі, є відомим у другій, а те, про що запитується у другій задачі, є відомим у першій.

Складання оберненої задачі можна застосовувати до будь-якої задачі, але воно громіздке. Інколи учні можуть скласти таку обернену задачу, яку потім не здатні розв’язати. Тому, формулюючи це завдання, вчителю доцільно вказувати, яке значення величини треба зробити шуканим.

Задача. В одному мотку 32 м дроту, а в другому на 15 м менше. Скільки метрів дроту в обох мотках?

Завдання. Розв’язати задачу. Скласти обернену задачу, в якій треба знайти, на скільки метрів дроту менше в другому мотку, ніж у першому.

2. ТВОРЧА РОБОТА НАД КОНКРЕТНОЮ ЗАДАЧЕЮ

Щоб учні зрозуміли сутність структури задачі й механізму її розв’язування, необхідно дати їм можливість бачити, на що впливають ті чи інші зміни в задачі, як можна одержати дану задачу з раніше розв’язаних, як можна розкласти дану задачу на задачі відомих видів, в які задачі вона входить як складова.

Змінюючи ту чи іншу частину задачі або її формулювання, можна показати учням суттєві й несуттєві частини умови і запитання.

Зміни задач, що не змінюють їх структури.

Зміна числових даних.

Кожного разу вчитель ставить мету, якої він хоче досягти такими змінами (узагальнити розв’язання, показати неможливість розв’язання у заданій множині чисел, зменшити складність задачі, довести, що величина чисел не впливає на розв’язування і вибір дій у розв’язанні). Заміна даних меншими числами не лише сприяє узагальненню способу розв’язування задач даного виду, а й допомагає учням краще зрозуміти залежності між величинами і те, як великі числа відволікають деяких учнів від змісту задачі. Замінивши великі числа меншими, учням легше знайти план розв’язування даної задачі та правильно вибрати дію для її розв’язання.

Задача. У Михайлика 25 марок, а у Петрика на 10 марок більше. Скільки марок у Петрика?

Після розв’язання задачі можна запропонувати замінити число 25 числом 20 і розв’язати отриману задачу. З’ясувати, чи змінилась дія у розв’язанні.

Можна запропонувати і такі варіанти завдань:

Замінити обидва числові дані й розв’язати задачу.
Замінити числові дані так, щоб шукане число збільшилось (зменшилось).
Замінити числа так, щоб у результаті одержати число, більше 100.

У деяких випадках можна запропонувати учням змінити числові дані так, щоб задачу можна було розв’язати іншим способом.

Задача. У 2 клітках було по 5 кролів у кожній, а в 4 клітках — по 6 кролів. Скільки всього було кролів?

Завдання. Замінити числа так, щоб задачу можна було розв’язати двома способами.

Для виконання завдання необхідно зрівняти або число кліток, або число кролів у клітках.

Зміна порядку слідування чисел.

Відомо, що молодші школярі при виборі дій часто керуються тим, чи написані числові дані поряд. Аби показати їм, що порядок слідування чисел не впливає на план та вибір дій, доцільно давати завдання:

Скажіть умову задачі так, щоб перше число стояло не першим.
Скажіть умову задачі так, щоб пов’язані між собою пари чисел стояли поряд.

Замінюючи порядок слідування чисел, учитель може збільшити або зменшити складність задач.

Зміна місця запитання.

Інколи учні недостатню увагу приділяють запитанню задачі. Постановка запитання на перше місце не тільки змінює звичайний порядок слідування частин задачі, а й створює елемент проблемності.

Спочатку вчитель сам проговорює задачу, яка починається запитанням, а учням пропонується сформулювати умову задачі так, щоб запитання було відокремлене від умови. Пізніше можна давати завдання:

Замініть формулювання задачі, щоб вона починалась запитанням.
Чи зміниться розв’язання задачі?

Зміна формулювання задачі.

Більша частина запитань задач підручників містить слово «скільки». Тому учні розуміють запитання як речення зі словом «скільки». Доцільно показати їм, що запитання може бути реченням у питальній формі без слова «скільки» або в наказовій формі. Спочатку з різними формулюваннями запитання дітей ознайомлює сам учитель. Пізніше пропонує учням завдання: «Замініть запитання, щоб у ньому було слово «скільки»; «Замініть запитання, щоб розв’язання не змінилося».

Зміна сюжету задачі.

Метою такої зміни є розуміння учнями того, що в задачі головним є відношення між значеннями величин, а не сюжет; розвиток у них здатності бачити спільне у відмінному.

Задача. Купили по 4 м вовняної й лляної тканини. Ціна вовняної тканини 80 гри за метр, а лляної — 30 грн. Знайдіть вартість покупки.

Після розв’язання задачі пропонується скласти задачу з таким самим розв’язанням, але щоб у ній говорилося про зустрічний рух.

2.2. Зміни елементів задачі, які змінюють її структуру.

Помилки, яких припускаються діти при розв’язуванні задач, часто виникають через те, що виявляються не усвідомленими деякі важливі елементи задачі або незрозумілим є запитання задачі. Тому доцільно подати задачу в її розвитку, в поступовому ускладненні. Учні мають можливість бачити, як нові умови впливають на розв’язок задачі.

Зміна запитання.

Застосування прийому підкреслює спрямувальну роль запитання для вибору необхідних зв’язків, стимулює учнів до всебічного аналізу задачної ситуації. Зміну запитання використовують також для постановки нових задач, «розширення» задачі.

Зміну запитання використовують часто для того, щоб показати відмінності між складеною і простою задачею. З цією метою учням даються завдання: «замініть запитання, щоб задача розв’язувалась двома діями». Таке завдання сприяє розумінню учнями також способу утворення складених задач із простих.

Учитель може сам пропонувати змінені запитання, а учні пояснюють, як змінюється розв’язок.

Задача. У класі 24 хлопці і 6 дівчат. Скільки всього учнів у класі?

Після розв’язування задачі вчитель пропонує замінити запитання такими:

На скільки хлопців більше, ніж дівчат?
У скільки разів хлопців більше, ніж дівчат?

Працюючи зі складеними задачами, можна пропонувати дітям завдання: «Змініть запитання задачі так, щоб у розв’язанні не треба було виконувати останню дію» або «Змініть запитання задачі так, щоб у розв’язанні додалась іще одна або більше дій».

Задача. Довжина городу прямокутної форми 72 м, а ширина в 2 рази менша. 1/3 площі городу зайнято різними овочами, а решту — картоплею. Скільки квадратних метрів городу зайнято картоплею?

Після розв’язування задачі можна запропонувати учням: «Замініть запитання так, щоб у розв’язанні додалась іще одна дія — віднімання».

Зміну запитання можна використати, аби показати, що кількість дій у розв’язанні не зміниться, а зміниться лише остання дія.

Задача. Посадили 4 ряди берез, по 15 у кожному ряду, і 20 лип. Скільки всього дерев посадили?

Після розв’язання задачі вчитель пропонує змінити запитання так, щоб останньою дією було віднімання (ділення).

Зміна запитання деяких складених задач може привести до зміни всього розв’язання, тобто до утворення на основі даного сюжету нової задачі.

Задача. Токар за 16 днів виточив 240 деталей. Потім, щоб виконати план, він за 8 днів виточив 264 такі самі деталі. Скільки деталей повинен був виточувати токар кожного дня за планом?

Розв’язання задачі:

240 + 264 = 504 (д.);
16 + 8 = 24 (дн.);
504 : 24 = 21 (д.).

Змінене запитання: на скільки деталей більше став виточувати токар кожного дня? Розв’язання одержаної задачі:

240 : 16 = 15 (д.);
264 : 8 = 33 (д.);
33 - 15 = 18 (д.).

Така зміна запитання може використовуватись у подібних задачах на рух, про витрату кормів тощо.

Робота над зміною запитання має не лише методичну цінність, вона також активізує розумову діяльність учнів. Така робота акцентує увагу на ролі запитання і сприяє розумінню учнями того, що перед розв’язуванням задачі необхідно усвідомити мету майбутньої роботи.

Зміна деяких зв’язків в умові задачі.

Такий прийом привертає увагу дітей до значення окремих слів і виразів у тексті задачі. Поступово учні усвідомлюють, що незначні, на перший погляд, зміни приводять до істотних змін у розв’язуванні.

Порівнюючи задачі: 1) «В ящику було 10 кг слив. Поклали ще 3 кг слив. Скільки слив стало в ящику?» і 2) «В ящику було 10 кг слив. Взяли 3 кг слив. Скільки слив стало в ящику?», — учні бачать, що зміна тільки одного слова в умові може змінити вибір дії в розв’язанні.

Корисно вводити зміни, які вимагають від учнів уміння розрізняти близькі між собою поняття.

Задача. Довжина ручки 12 см, а олівець на 3 см коротший. Яка довжина олівця?

Завдання.

Замініть слово «коротший» словом «довший». Що змінилось у розв’язанні?
Замініть в умові вислів «на 3 см» висловом «у 3 рази» і розв’яжіть одержану задачу.

Розглянуті зміни доцільно здійснювати не лише у простих, а й у складених задачах.

Задача. В автобусі їхало 24 дорослих, а дітей у 3 рази менше. Скільки всього пасажирів їхало в автобусі?

Завдання. Замініть частину умови, щоб у розв’язанні першою дією було віднімання (додавання, множення).

2.2.3. Розширення задач.

Для формування правильних уявлень учнів про структуру задачі і процес її розв’язування важливо показати задачу в її розвитку, в поступовому її розширенні. Розширити задачу можна:

а) доповнивши умову деякими числовими даними, не змінюючи запитання;

б) продовживши події, описаны в умові, й відповідно змінюючи запитання;

в) замінивши деякі числа умовами простих задач (виразом), не змінюючи запитання.

Розглянемо приклади.

а) Задача. Мама купила 5 кг огірків, 2 кг помідорів і 3 кг яблук. На скільки кілограмів більше мама купила овочів, ніж фруктів?

Які ще фрукти могла купити мама?
Доповніть умову вказівкою, що мама купила ще 1 кг груш. Розв’яжіть отриману задачу. Що змінилось у розв’язуванні?

Пізніше можна пропонувати учням завдання виду: доповніть умову задачі числами, не змінюючи запитання, щоб у розв’язанні з’явилась іще одна дія.

Головним варіантом цього виду роботи є звуження задачі, коли учням пропонується вилучити з умови одне із числових даних, не змінюючи запитання.

Задача. В магазин привезли 9 ящиків яблук, по 20 кг у кожному. За перший день продали 60 кг яблук, за другий — в 2 рази менше, за третій — 50 кг. Скільки кілограмів яблук залишилося?

Завдання. Вилучіть з умови частину, де сказано про яблука, продані третього дня, і розв’яжіть одержану задачу. Що змінилось у розв’язанні?

б) Продовження події в умові й зміна запитання задачі збігається з одержанням складеної задачі із простих, що перебувають у відношенні «продовження».

Задача. Коля зібрав 5 кг грибів, а Оля — на 2 кг більше. Скільки грибів зібрали разом Коля і Оля?

Завдання. Що могли зробити із зібраними грибами? Доповніть задачу вказівкою: 4 кг грибів законсервували, а решту засушили.

Запитання. Скільки кілограмів грибів засушили?

Скажіть умову одержаної задачі. Що змінилось у розв’язанні?

в) Розширення через додавання числових даних дає можливість вводити одночасно складені задачі різної математичної структури з одним і тим самим запитанням; зіставляти умови задач і їх розв’язання.

Задача. Коля і Толя саджали дерева. Коля посадив 10 дерев, а Толя — 8. Скільки дерев посадили Коля і Толя разом?

Після вивчення задачі учитель може провести бесіду і одночасно креслить схему.

Чи відомі обидва числа, необхідні для розв’язання задачі? (Учитель будує схему 1.)
Чи можна було б розв’язати задачу, якби не було відомим число 10? (Учитель закреслює число 10 і ставить знак питання (див. схему 2).)

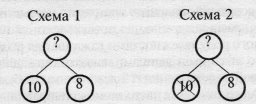
А які два числа треба знати, щоб знайти число 10? Чи могли б ми дізнатися, скільки дерев посадив Коля, якби знали, які дерева він садив? Нехай Коля посадив 6 яблунь і 4 груші. Одержуємо задачу: Коля посадив 6 яблунь і 4 груші, а Толя — 8 дерев. Скільки дерев посадили Коля і Толя разом?

Розв’яжемо одержану задачу. Ми із простої задачі отримали задачу на дві дії, зробивши одне з відомих чисел невідомим і вказавши, як його можна знайти.

Як, користуючись схемою, можна одержати задачу на три дії, щоб в умові було слово «менше», а відповідь не змінилася?

Узагальнюємо: заміна числа умовою простої задачі додає в розв’язання одну дію, за допомогою якої знаходимо число, яке замінюємо.

Задача. Турист за день пройшов 10 км і проїхав на автобусі 180 км. Яку відстань подолав турист за день?

Завдання.

а) Замініть число 10 умовою, щоб у розв’язанні додалась дія множення, а відповідь не змінилася.

б) Що зміниться в розв’язанні, якщо число 10 замінити умовою: «Турист ішов 2 год зі швидкістю 5 км/год», а число 180 — умовою «автобусом він їхав на 1 год більше зі швидкістю 60 км/год»?

Цінним у такому розширенні задачі є те, що відповідь не змінюється, а вся розумова діяльність учнів спрямована на аналіз ситуації та обґрунтування вибору необхідних дій і їх послідовності.

Використання різних типів пам'яті для розв'язування задач

Як же допомогти всім учням навчитися розв'язувати задачі?

Практика переконує, що насамперед слід обов'язково враховувати тип пам'яті: зоровий, слуховий, моторний (руховий) і змішаний.

Зоровий — запам'ятовування через зоровий аналізатор;
слуховий—запам'ятовування за допомогою слуху;
моторний - запам'ятовування через рух кінцівок і органів мовлення;
змішаний — запам'ятовування і відтворення інформації через будь-який аналізатор.

Чому треба враховувати тип пам'яті? Можна навести безліч прикладів, коли деякі учні інколи безнадійно відстають у засвоєнні матеріалу і стають Педагогічно запущеними. Так, учитель щоденно бачить, як під час закріплення вивченого частина учнів засвоюють матеріал, а інші — ніби нічого не чули. І тут починаються нарікання класовода на неуважність, розсіяність учня. Але ж це не так! Учень хоче зрозуміти, але не може через те, що у нього інший тип пам'яті, наприклад, зоровий. І яким би уважним він не був під час сприймання, як би не напружував свою волю, але сприйняти матеріал належним чином на слух він навряд чи зможе. .

Тому, враховуючи типи пам'яті кожного учня, учителеві необхідно диференціювати дидактичні впливи. Це зовсім не просто, але цілком можливо, якщо учитель зможе чітко організувати одночасну роботу окремих груп учнів з використанням посібників з диференційованими завданнями.

Що ж дає такий підхід до навчальної діяльності? Насамперед учитель спрямовує свої зусилля на те, щоб розвивати в усіх учнів мислительні операції і водночас формує інтерес до навчання, старанність і вміння самостійно вчитися.

Саме такі конкретні приклади і розглянемо на фрагментах уроків математики в початкових класах, коли вчитель, опираючись на різні типи пам'яті, поступово формує у дітей абстрактне мислення.

Фрагмент уроку математики в 3 класі

Тема. Задачі на ділення суми на число.

(Посібник "Вчимося розв'язувати задачі", 3 клас, видавництво "Початкова школа", 2011).

І етап

Колективна робота. (Слуховий тип пам'яті).

Задача №7,с. 109.

В одному кошику 10 яблук, а в другому —11. Усі яблука розклали порівну на 3 тарілки. Скільки яблук на одній тарілці?

Колективний аналіз задачі, за допомогою планшетів виділяється перший варіант і група учнів, яким потрібна допомога.

II етап

1 варіант. Самостійно записати розв'язання задачі №7, с. 109.

Додаткове завдання: задача № 6, с. 108.

варіант. (Зоровий і моторний типи пам'яті).

Колективна робота над задачею № 8, с. 109.

Зрізали 9 жовтих і 3 червоних айстр. Усі айстри поставили порівну в 4 вази. Скільки айстр в одній вазі?

Працюють "художнику". Кольоровими олівцями "розставляють" 9 жовтих і 3 червоних айстр порівну в 4 вази.

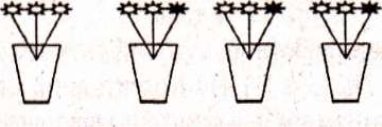
Після колективного аналізу задачі з коментуванням записують розв'язання даної задачі. Перевірка всіх завдань. Слухають усі.

III етап

1варіант. Задача № 10, с. 109.

Добери числові дані так, щоб у пакетах горіхів було порівну.

Маринка зібрала □ горіхів, а Михайлик — □. Усі горіхи розсипали в пакети, по 25 горіхів у кожний. Скільки використали пакетів?

2варіант. Задача № 2, с. 107.

Зверни увагу на короткий запис задачі і схематичний запис її розв'язання.

В Оленки було 40 к., а у Максима — 60 к. На всі гроші вони купили зошити, по 20 к. за кожний. Скільки всього зошитів купили діти?

3 варіант. Складання "живої" задачі. (Змішаний тип пам'яті).

Задача № 10, с. 109. Добери числові дані та розв'яжи задачу.

Маринка зібрала □ горіхів, а Михайлик — Усі горіхи розсипали в пакети, по 25 горіхів у кожний. Скільки використали пакетів?

Два учні беруть відповідну кількість горіхів і розкладають в пакети по 25 горіхів у кожний.

На таких прикладах учні легко добирають правильні арифметичні дії для розв'язання задач. Після колективного аналізу "живої" задачі учні самостійно записують її розв'язання.

Перевірка всіх завдань. Слухають усі.

Підсумкові завдання на вибір:

1варіант. Задача № 12, с. 109. Вилучи зайві дані та розв'яжи задачу.

З першого куща зібрали 9 кг червоної смородини, а з другого — 6 кг. Чорної смородини зібрали 2 кг. Усі ягоди червоної смородини розклали в банки, по 5 кг у кожну. Скільки використали банок?

2варіант. Задача № 5, с. 108.

З першого куща смородини зібрали 8 кг ягід, з другого — 12 кг. Усю смородину розклали порівну в пакети по 4 кілограми. Скільки використали пакетів?

Розв'язання:

8 + □ = □ (кг) - усього;
□: 4 = □ (кг) — кількість пакетів.

Відповідь: 5пакетів.

Фрагмент уроку математики в 4 класі

Тема. Задачі на знаходження середнього арифметичного.

(Посібник "Вчимося розв'язувати задачі", 4 клас, видавництво "Початкова школа", 2006)

Іетап

Колективна робота. (Слуховий тип пам'яті).

З а д а ч і № 2,3, с. 111,112. Колективний аналіз задач з використанням зразків запитань і відповідей до них.

Виділення першого варіанта і групи учнів, яким потрібна допомога.

ІІетап

1 варіант. Самостійно записати розв'язання задачі № 2, с. 111, користуючись зразком міркувань (с. 111, с. 112).

варіант. (Зоровий і моторний типи пам'яті).

Колективна робота над задачею № 4, с. 113.

Автомобіль 5 год їхав зі швидкістю 63 км/год, а 2 год — зі швидкістю 56 км/год. Знайди середню швидкість руху автомобіля.

Колективне складання графічного зображення руху автомобіля.

Використання зразка аналізу і розв'язання задачі, наведеного в посібнику. Самостійно записати розв'язання задачі за опорними позначеннями дій (с. 114).

Запиши розв'язання.

63  □ = □ (км) — проїхав автомобіль за 5 год;
56  □ = □ (км) — проїхав автомобіль за 2 год;
□+ □ = □ (км) — шлях, який проїхав автомобіль за ввесь час;
□+□ = □ (год) — час руху автомобіля;
□ : □ = □ (км/год) — середня швидкість автомобіля.

Перевірка всіх завдань. Слухають усі.

ІІІетап

1варіант. Задача № 10, с. 115.

Сформулюй запитання і розв'яжи задачу.

Робітник виготовив за першу годину 23 деталі, за другу — 25 деталей, за третю — 30. Скільки...?

Відповідь: 26деталей.

2 варіант. Користуючись зразком (задача № 6), розв'яжи самостійно задачу № 7, с. 114.

І Маса першої курки 2 кг 400 г, а другої — 3 кг. І Знайди середню масу цих курей.

3варіант. (Змішаний тип пам'яті).

Складання "живої" задачі № 5 з використанням алгоритму дій, наведеного в посібнику (с. 114).

Купили 3 м зеленої стрічки, по 2грн за 1 метр, і 7 м синьої стрічки, по 3грн за 1 метр. Знайди середню ціну стрічки.

Учні використовують іграшкову "касу", гривні і здійснюють покупку згідно з умовою задачі. Далі проводиться аналіз задачі за посібником:

Про що йдеться в задачі?
Що відомо про стрічку зеленого кольору?
Що відомо про стрічку синього кольору?
Про що запитується в задачі?

Міркуй далі сам

Робота в парах. Учні продовжують аналізувати задачу за зразком задачі № 2 (с. 111).

Колективно розібрати і самостійно записати розв'язання задачі за опорними схемами дій (с. 114).

□  □ = □ (грн) — вартість зеленої стрічки;
□  □ = □ (грн) — вартість синьої стрічки;
□+ □ = □ (грн) — вартість усієї стрічки;
□+ □ = □ (грн) — кількість метрів усієї стрічки;
□ : □ = □ (грн.) — середня ціна стрічки.

Перевірка всіх завдань. Слухають усі.

Підсумкові завдання.

1варіант. Задача № 12, с. 115.

Склади умову задачі до запитання та розв’яжи її.

Яка середня швидкість пішохода?

2варіант. Задача № 9, с. 115.

Поїзд пройшов за першу годину 54 км, за другу – 61км, за третю – 59км.

Знайди середню швидкість поїзда.

Завдання диференційованого підходу не можна зводити лише до того, щоб пристосовувати навчання до дитячих індивідуальних особливостей. Не менш важливо — впливати на їх формування, розвивати в учнів розумові та інші якості, які визначають успішне засвоєння програмового матеріалу і вдосконалюють здатність дітей до окремих видів навчальної діяльності.

Диференційовані завдання

Необхідною умовою успішного навчання математики є якнайповніше використання потенційних можливостей кожного учня. Досягти-цієї мети нелегко, адже діти по-різному сприймають і засвоюють навчальний матеріал. Завдання, що не викликає труднощів в одного учня, для іншого виявляється за складним. Тому вчитель, готуючись до уроку, визначає не тільки його загальну навчально-пізнавальну мету, а й способи досягнення її кожним учнем. У цьому, зокрема, й допоможуть диференційовані завдання. Вони мають поєднати навчальний процес усього класу з допомогою учням, які повільніше сприймають матеріал, і постійним удосконаленням сильних учнів. У завданнях передбачено послідовний перехід від простих до складніших. При цьому диференційована робота спрямована на розвиток в усіх учнів самостійності та інтересу до навчання.

Оскільки в умовах класно-урочної форми навчання програмний матеріал подається одночасно для всіх учнів, то для диференційованої роботи здебільшого пропонуються завдання, що мають спільну пізнавальну мету, але відрізняються за ступенем складності.

Щоб забезпечити чіткість етапів уроку, організований перехід від одного виду навчальної роботи до іншого, додаткові завдання дібрано так, щоб роботу над ними можна було припинити в будь-який час, незалежно від того, чи закінчили учні розв’язувати ці завдання.

Прийоми диференціювання завдань різні, основні з них такі: полегшення змісту; ускладнення його на основі додаткових вимог, зазначених в інструкції; різноманітні способи допомоги у виконанні завдань, а саме: конкретизація завдання, наведення початку його розв’язання, зразка розв’язання, плану або схеми розв’язання, а також інформації, потрібної для виконання завдання.

У багатьох випадках диференціація може полягати в тому, що учень виконує ту частину завдання, яку встигає зробити за визначений учителем час. Диференціації сприяють і додаткові завдання. За змістом це переважно завдання з логічним навантаженням.

С - 1

1. Запиши у вигляді прикладів відповіді на запитання.

Як утворити число 90 із попереднього щодо нього числа?
Як утворити число 29 від наступного за ним числа?
Скільки дістанемо, якщо від числа 38 віднімемо число його десятків?

Кожне з таких чисел: 21, 63, 36, 33 запиши у вигляді суми його розрядних доданків.
Запиши всі двоцифрові числа, які можна утворити із цифр 3, 8, 9. Повторювати одну й ту саму цифру можна.
Розв’яжи задачу.

У першій бригаді 25 тракторів, а в другій менше. Коли з першої в другу переїхало 5 тракторів, то в обох бригадах тракторів стало порівну. Скільки тракторів було в другій бригаді спочатку?

С — 2

Для сівби озимини бригадир виділив на першу ділянку 4 тракторні сівалки, на 2 сівалки менше, ніж на другу ділянку. Скільки всього сівалок було на обох ділянках? Розглянь малюнок і розв’яжи задачу.

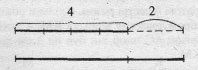
Розв’яжи тільки ті з поданих рівнянь, у яких невідомим є доданок.

х - 7 = 23

23 - х = 7

3 + х = 27

Накресли один відрізок завдовжки 12 см, а другий на 1 дм коротший.
Розв’яжи задачу.

У дівчинки стільки сестер, скільки й братів. Брат сказав, що в нього 3 сестри. Скільки всього дітей у сім’ї?

С-3

Розв’яжи приклади з перевіркою.

28 + 2 74 + 8

Розв’яжи приклади.

4 + 9 11-8

0+1 66-13

85 + 7 42 -5

10 -0 66 + 13

Розв’яжи задачу, склавши рівняння.

У кошику було 27 грибів. Коли в нього поклали ще кілька грибів, їх стало 30. Скільки грибів поклали в кошик?

Запиши вирази і обчисли їх значення.

Сума чисел 28 і 5; 13 і 7.
Зменш 52 на 8.
До числа 20 додай різницю чисел 13 і 7.

Розв’яжи задачу.

Братові 12 років, а його сестрі 7. Скільки років буде братові, коли сестрі стане стільки, як йому тепер?

С — 4

Відстань між двома пунктами — 80 м. Із цих пунктів назустріч один одному вийшли два хлопчики. Перший хлопчик пройшов 25 м, а другий 29 м. Скільки метрів їм залишилося пройти до зустрічі?

Розв’яжи задачу, склавши, вираз на віднімання суми від числа.

Розв’яжи приклади.

58 + 25 26 - 18 56 + 25

17 + 68 95 - 48 33 - 16

Примітка. Треба спочатку додати або відняти десятки, а потім одиниці.

Спиши, заповнюючи пропуски.

90 см = ... дм 8 дм 1 см = ... см

З дм = ... см 53 см = ... дм ... см

Розв’яжи задачу.

Маринка гостювала в бабусі 2 тижні й 6 днів. Скільки всього днів була Маринка в бабусі?

С — 5

Розв’яжи приклади, додаючи десятки до десятків, одиниці до одиниць.

12 + 25 37 + 54 68 + 15

Встав знаки >, <, =.

19 — 0 ... 20 — 1 5 дм ... З дм 2 см

64- 8 ... 64 - 6 37 ... 40 -7

Розв’яжи задачу.

Братові 9 років, сестрі — 13, а батькові на 12 років більше, ніж братові й сестрі разом. Скільки років батькові?

Виміряй довжину відрізка КМ, а потім побудуй такий відрізок АС, щоб він був на 3 см довший, ніж відрізок КМ.

5.Розв’яжи задачу.

На двох тарілках лежало по 12 горіхів. З першої тарілки хлопчик узяв 7 горіхів, а дівчинка з другої тарілки взяла стільки, скільки горіхів залишилося на першій тарілці. Скільки горіхів узяли хлопчик і дівчинка разом?

С-6

1. Знайди:

а) доданок, якщо сума дорівнює 18, а відомий доданок 14;

б) від’ємник, якщо зменшуване 33, а різниця 16.

Добери такі числа, щоб нерівності були правильними.

27 < ... + 5 14 + ... >20 13 - ... < 6

За коротким записом склади, а потім розв’яжи задачу про молоко в бідоні.

Було — ?

Витратили — 5 і 7.

Залишилось — 8.

Обчисли значення кожної суми і кожної різниці

а	23	50	12	67	77	41
к	7	16	8	18	25	0
а-к	16
а +к	30

На скільки 1 м довший від 1 см?

С — 7

Склади такі чотири приклади на додавання, щоб їх можна було записати як приклади на множення.

Зразок: 3 + 3 + 3 + 3 + 3 = 3 • 5

Запиши розв’язання задачі спочатку додаванням, а потім множенням.

Блокнот коштує 12 грн. Купили 3 таких блокноти. Скільки за них заплатили?

Запиши розв’язання й відповідь задачі.

15 л соку розлили в банки, по 3 л в кожну. Скільки використали банок?

Примітка. Виконай ділення за допомогою паличок.

Маринка й Оленка складали задачі. Маринка запропонувала Оленці таку задачу: «У юннатів було З клітки, а кролів 4. Скількома способами можна розмістити кролів у клітках?».

С - 8

1. Накресли таку фігуру, як на малюнку. Запиши назву фігури. Виміряй довжину найбільшої її сторони.

2. Виміряй відрізки й запиши довжину кожного з них у сантиметрах та в міліметрах. Побудуй відрізок, який дорівнює відрізкові МС.

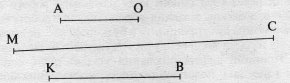
3. 20 горіхів розклали на 5 купок, порівну в кожній. Скільки горіхів в одній купці?

Замість горіхів розклади палички, а потім запиши розв’язання задачі.

С -9

1. Склади, користуючись малюнком, один приклад на множення і два на ділення.

З кожного прикладу на множення склади приклади на ділення й запиши відповіді.

4∙2 = 8 7∙5 = 35 9∙3 = 27

У майстерні було 2 сувої тканини, по 24 м в кожному. 16 м тканини витратили на пошиття дитячих костюмів. Скільки метрів тканини залишилося?

С- 10

У класі було 24 хлопчики і 16 дівчаток. 6 хлопчиків вийшли на подвір’я. Кого стало в класі більше — хлопчиків чи дівчаток? На скільки більше?
Скільки потрібно паличок, щоб скласти 6 окремих трикутників?
Знайди частку чисел 9 і 3.
Постав до кожної задачі запитання і знайди відповіді.

14 стільців розставили в 2 ряди, порівну в кожному.
14 стільців розставили в ряди, по 2 стільці в кожному.

Розв’яжи рівняння.

х • 3 = 12 8 • х = 16

С- 11

Розглянь умову задачі та початок її розв’язання, а потім закінчи її розв’язувати.

На п’ять підвід поклали мішки зерна, по 6 мішків на кожну. На машину поклали 36 мішків. На скільки більше мішків зерна поклали на машину, ніж на всі підводи?

Розв ’язання:

6 • 5 = 30 (м.)

6 + 6 + 6 + 6 + 6 = 30

36 - ... = ...

Заміни в задачі запитання на таке: скільки мішків зерна поклали на підводи й машину разом? Розв’язання нової задачі запиши в зошит.

Розв’яжи приклади.

1∙ 7 (14 - 7) • 1 1 • (52 - 3)

8-1 (6 + 4) • 1 1 • (9 + 49)

Виконай завдання, записавши умову.

Знайди добуток чисел 8 і 2.
Ділене — 14, дільник — 7. Знайди частку.
Зменшуване — 16, різниця — 8. Знайди від’ємник.

С - 12

Користуючись прикладом на додавання, склади приклад на множення, а потім — два приклади на ділення.

4+4+4+4+4+4

Зразок:

3 + 3 + 3 + 3 + 3=15 3 • 5= 15

15 : 3 = 5 15 : 5 = З

Знайди результат другого прикладу, користуючись першим:

3∙8 = 24 36:9 = 4 12:6 = 2

24 : 3 9-4 12 : 2

Від’ємник виражений сумою чисел 1 і 28, зменшуване дорівнює 70. Знайди різницю.
Обчисли «ланцюжки».

+2 7:7 3-10 4:4

-12 ... + 39 ... - 15 ... + 1

- 7 ... : 4 ... : 1 ... • 1

С- 13

За зразком до кожного випадку множення числа З склади три інші приклади.

Зразок:

3•7 = 21 7•3 = 21 21:3 = 7 21:7 = 3

3 • 8 = 24 8 • 3 = 24 : 3 = ... : ... =

3 • 9 = 27 ... • ... = ... : ... = ... : ... =

Розв’яжи кругові приклади:

2•6 6+4 4•2 8•3 3•3

10 : 5 12 : 3 9•2 18 : 3 24 : 8

В одному бідоні 12 л молока, а в другому на 6 л більше. Все молоко з другого бідона розлили в банки, по 3 л в кожну. Скільки потрібно було банок?
Накресли відрізок завдовжки 12 см і поділи його на частини, щоб кожна дорівнювала 3 см. Скільки утвориться частин?
Запиши всі числа, кожне з яких не більше від 30 і ділиться на 3.

С - 14

Протягом тижня (5 робочих днів) робітники ремонтували щодня по 3 комбайни. їм залишилося ще відремонтувати 9 комбайнів. Скільки всього комбайнів потрібно було відремонтувати?
Розв’яжи приклади.

2•10 4:2 34 + 18 (3 + 15) : З

3•8 18 : 9 81 - 27 (11 - 3) : 4

Розв’яжи рівняння.

14 - х = 7 14 : х = 7

Запиши таблицю ділення на 3 до кінця.

6:3 = 2 9:3 = 3 12:3 =

Маса індика — 8 кг, а маса півня — в два рази менша. Яка маса півня?
З 10 паличок склали 3 однакових квадрати. Які дві палички треба забрати, щоб залишився нерівносторонній прямокутник?

С -15

1. У скільки разів перша смужка довша від другої

Виміряй довжину кожної смужки й перевір відповідь обчисленням.

Розв’яжи приклади, додержуючи правил щодо порядку виконання арифметичних дій.

18 - 8:2 60 : 10 : 2 (24 - 16) : 4

2 + 8•4 10 • 2 : 4 7 • (10 - 7)

Перше число — 9, а друге у 3 рази більше. Чому дорівнює сума цих чисел?
Є дві посудини. Місткість однієї посудини — 3 л, другої — 5 л. Як, користуючись цими посудинами, налити у відро 4 л води?

С - 16

1. Арифметичний диктант.

Зменш 14 на 7.
Збільш 10 у 5 разів.
Зменш 30 у 6 разів.
Знайди частку чисел 48 і 6.
Знайди добуток чисел 6 і 9.
У скільки разів 54 більше від 6?

Скільки треба паличок, щоб скласти 7 окремих шестикутників?
З ряду чисел 1, 5, 9, 13, 17 випиши ті значення букви к, за яких правильна нерівність к + 17 < 30.
У касира є монети вартістю 2 к. і 5 к. Скількома способами він може дати 20 к. здачі?

С- 17

Запиши таблицю множення на 6.

2• 6 = 12 3 • 6 = ...

Яке число треба зменшити в 6 разів, щоб отримати 10?

3.На пошиття 4 однакових костюмів витратили 12 м тканини. Скільки потрібно метрів тканини, щоб пошити 6 таких костюмів?

Розв’яжи рівняння, в якому невідомим є ділене.

х — 6 = 18

х • 6 = 18

х : 6 = 8

На передніх лапках у білки по 4 пальці, а на задніх — по 5. Скільки всього пальців на лапках у білки?

С- 18

Обчисли «ланцюжки» й додай усі відповіді.

7•7 0+10 1•9 18 - 9

-29 •4 : 3 •7

: 4 : 5 • 7 - 7

5 : 8 - 3 : 8

У Михайлика є 4 монети по 1 к., а в Остапа — 9 монет по 5 к. У кого з хлопчиків більше грошей і на скільки?
Розв’яжи рівняння.

51 -х= 7 + 21

Щоб піднятися на четвертий поверх будинку, треба пройти 60 східців. Скільки східців треба пройти, щоб піднятись на шостий поверх цього будинку? Кількість східців між цими поверхами однакова.
На двох кущах сиділо 20 горобців. З першого куща 4 горобці знялися в повітря, а 3 перелетіли на другий кущ. Після цього на обох кущах стало горобців порівну. Скільки горобців було на кожному кущі спочатку?

С - 19

Арифметичний диктант.

У скільки разів 8 більше від 1?
Чому дорівнює різниця чисел 24 і 8?
Зменш 49 у 7 разів.
Збільш 9 на 3.
Яке число більше, ніж 6, у 3 рази?

Розв’яжи приклади.

72 : 8 7•7 1 • 5 15 - 6 24 : 6 • 2

27: 9 56 : 8 5•9 37 + 49 64 + 16 : 8

Розв’яжи рівняння.

21 : х = 3 12 - х = 3 • 2.

Запиши вирази й обчисли їх значення:

Перший множник 8, а другий виражений сумою чисел 6 і 4.
Зменшуване виражене часткою чисел 42 і 7, а різниця 5.
Ділене є сумою чисел 5 і 35, а дільник дорівнює 5.

Розстав дужки так, щоб рівність була правильною.

24 : 8 - 2 = 4

Які із тверджень правильні?

70 більше від 90 на 20.
1 м = 100 см.
Квадрат не є прямокутником.

С — 20

Розглянь два способи обчислення виразу (2 + 8) - 5 і поясни кожний з них.

спосіб

(2 + 8) • 5 = 10 • 5 = 50

спосіб

(2 + 8) • 5 = 2 • 5 + 8 • 5 = 10 + 40 = 50

Розв’яжи двома способами.

(4 + 5) • 8

З поданих виразів обчисли тільки ті, що є добутками.

20 : 5 20 + 3•9 24:6 + 3 3 • 5 + 7 • 8

10•7 (3 +7)•5 8•(1 + 0) 13-8-5

Усно склади задачу за рівнянням, х = (50 : 5) • 8

Запиши її запитання, розв’язання й відповідь.

Блокнот коштує 6 грн., а книжка в 9 разів дорожча. На скільки блокнот дешевший за книжку?
Побудуй квадрат із периметром 16 см.

С — 21

Запиши всі двоцифрові числа, які менші від 50 і діляться на 5.
Обчисли, замінивши круглі числа десятками.

100 : 2 80 : 4 20 • 3 30•3

60 : 30 80 : 40 100 : 20 60 : 30

Зразок. 40 : 20 = 2, бо 20 • 2 = 40.

На початку року в дітей було 8 кролів, а наприкінці їх стало в 4 рази більше. На скільки більше кролів стало наприкінці року?
Розв’яжи кругові приклади.

9•8 72 - 12 28 : 4 6•6 4 •8

63 : 7 7•9 60 : 10 32 - 4 36:9

Число поділили на 5 і отримали 1. Яке це число?
Які три числа треба перемножити, щоб отримати 8?

С — 22

Слюсар за дві години виготовив 18 деталей. Скільки деталей вів зробить за 6 годин, коли щогодини виготовлятиме на одну деталь більше, ніж раніше?
Розв’яжи приклади.

60 : 3 2•50 9•4 35 + 49 (8 + 7) • 3

80 : 20 10 : 1 54 : 6 35 - 19 24 + 6 : З

Добери 4 значення букви с і 4 значення букви к, за яких с : к = 5.
Порівняй і постав знак >, < або =.

7 • 3 + 7 • 5 ... 7 • (3 + 4)

0-5 + 28 ... (5 - 1) + 28

12- (6 + 3) ...12-6 + 3

28: 4 ... 28 : 7

Один учень за тиждень отримав 6 оцінок. Подумай, чи є в нього оцінки, які повторюються.
Користуючись першим прикладом, знайди зручним способом суму чисел у другому й третьому прикладах.

3 + 8 + 6 = 17

13+ 18 + 16

23 + 28 + 26

С - 23

Виконай множення, застосовуючи правила множення числа на суму.

5•6 2•15 7•14 2•44

У шістнадцятиквартирному будинку провели електрику. В 9 квартирах було по 6 лампочок, а в кожній із решти квартир — на одну лампочку менше. Скільки всього лампочок було в решті квартир?
Розв’яжи приклади стовпчиками.

20•2 30•3 4•20

9 • 2 2 • 3 4•4

29•2 32•3 4•24

З дроту зробили рівносторонній трикутник і шестикутник. На обидві фігури витратили 54 см дроту. Знайди периметр шестикутника, якщо його сторона дорівнює стороні трикутника.

С-24

Розглянь розв’язання прикладу.

48 : 2 = (40 + 8) : 2 = 40 : 2 + 8 : 2 = 20 + 4 = 24

Розв’яжи таким самим способом приклади, але записуй лише умову й відповідь.

68 : 2 63 : 3 88 : 2

Розв’яжи приклади.

19 - 38 2 • 37 48 : 4 3 • 5 - 5 • 2

(48 - 16) : 8 100 : 50 30 : 2 70 - (12 + 18)

Примітка. У прикладі 30 : 2 одним із зручних доданків буде 20.

На 3 великих альбоми і 2 малих витратили 78 аркушів паперу. На кожний великий альбом витрачали 18 аркушів. Скільки аркушів витрачали на малий альбом?

Примітка. Знайди спочатку, скільки аркушів витратили на 2 малих альбоми.

Розв’яжи рівняння.

(48-х) + 12 = 21

Дано вираз с + к. Запиши вираз, який у 3 рази менший від даного.

С -25

Виконай ділення й перевір розв’язання множенням.

84 : 3 80 : 5

Згадай, що отримаємо, коли частку помножимо на дільник.

Морква в 4 рази дорожча від картоплі. Господиня купила 6 кг картоплі й заплатила 54 к. Моркви вона купила 2 кг. Скільки господиня заплатила за моркву?
Накресли три відрізки: перший завдовжки 72 мм, другий — у 3 рази коротший від нього, а третій — на 3 мм довший від другого.
Пара коней пробігла 24 км. Скільки кілометрів пробіг кожен кінь?
Є дві гирі: одна — 5 кг, а друга — 3 кг. Як за допомогою їх відважити 14 кг пшона?
Поділи 100 на дві частини так, щоб одна частина була на 20 більша від другої.

С — 26

Користуючись малюнком, розв’яжи приклад на ділення з остачею.

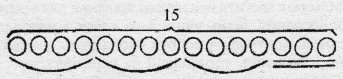
У дійниці було 9 л молока. Ним наповнили 4 глечики місткістю 2 л кожний. Скільки літрів молока залишилось у дійниці? Запиши розв’язання задачі у вигляді прикладу на ділення з остачею.
Порівняй приклади кожної пари й розв’яжи їх:

25 : 5 = 5 12 : 4 20 : 5 36 : 6

27 : 5 = 5 (ост. 2) 14 : 4 23 : 5 39 : 6

32 кг борошна продавець розфасував порівну в

пакетів. Скільки потрібно таких пакетів, щоб розфасувати 70 кг борошна?

С - 27

На кролефермі в кожній із 12 кліток по 2 кролі й у кожній із великих кліток по 8 кролів. Усього в клітках 84 кролі. Скільки великих кліток на кролефермі?
Розв’яжи приклади.

60 : 7 80 : 16 2•47 36:6+6:2

35 : 6 54 : 3 72:8 80-(35-28)

Розв’яжи рівняння.

41 - (х - 7) = 25 18 : х=3

Розглянь малюнок. Виміряй і запиши, чому дорівнює радіус круга. Запиши, які з позначених точок лежать у крузі.

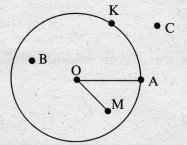
5. Після розмелювання жита виходить 6 частин борошна і 2 частини відходів. Скільки буде борошна, якщо змолоти 96 кг жита?

Урок з математики (4 клас)

Тема. Поняття про площу. Квадратний сантиметр

Мета:

ознайомити учнів з новою величиною – площею;
виправляти учнів в обчисленні виразів, які містять дію множення багатоцифрових чисел;
вчити розв’язувати задачі на сумісні дії;
розвивати логічне мислення, просторові уявлення;
виховувати інтерес до вивчення математики.

Обладнання: таблиці, схеми-опори, індивідуальні картки, малюнки зими та зимових місяців.

Хід уроку

І. Організаційний момент.

ІІ. Каліграфічна хвилинка.

60 км 2 години 70км/год

1год 30хв 50сек 800км 504м

ІІІ. Контроль і закріплення знань

усні обчислення за картками

поєднати приклади з однаковими відповідями

розв’язати задачу за кресленням

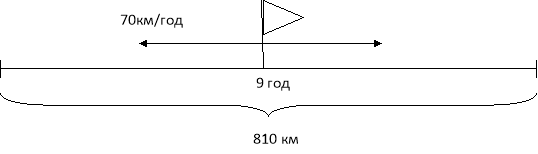
Гра-естафета «Хто швидше?» (на сніжинках приклади)

790 – 370	990 - 360	580 – 330
430 + 540	150 + 540	630 + 110
81 : 9 + 0	24 : 3 + 0	36 : 4
Х + 50 = 120	150 + х = 490	880 – х = 360

Контроль і корекція. Оцінювання знань.

Молодці, діти! Всі справились із завданням. Зима вами дуже задоволена, а тому приготувала свій наступний подарунок.

ІV. Оголошення теми та мети уроку.

Зима багата святами. Які зимові свята ви знаєте? (День Наума, День Святого Миколая, Новий рік, Різдво, Водохреща).
Всі ці свята різні. Але всі вони приносять дітям радість, веселощі, різні цікаві забави та подарунки. Святий Миколай приніс до нас ялинку, яку прикрасили штучними іграшками, кульками. На кожній кульці завдання.
Сьогодні ми маємо засвоїти, що таке площа та квадратний сантиметр.

V. Вивчення нового матеріалу.

1) Підготовча робота. (підготувала пошукова група «Комета»)

- Порівняти відрізки за довжиною (спочатку на око, потім - вимірюванням).

Порівняти площу кругів, зірочок, прямокутників. Як можна це зробити?

(зробити виставку різного кольору)

Висновок: Порівняти площу двох фігур можна на око. Іноді це роблять накладанням однієї фігури на іншу.

Площі різних фігур чи многокутників з різними сторонами порівнювати важче.

2) Групова робота

1 - зі сторонами 4 см і 9 см

2 - зі сторонами 7 см і 5 см

Обидва прямокутники поділено на однакові квадратики. Полічіть ці квадратики.
1-й – 36 квадратиків
2-й – 35 квадратиків

Первинне закріплення за впр. 466

Площа кола менша за площу чотирикутника.
Площа – це величина, яку можна не тільки порівнювати, але і вимірювати. Порівняйте на око площу фігур на малюнку.
Для вимірювання величини використовують одиниці вимірювання. Існують одиниці вимірювання і для площі. Невеликі площі вимірюються квадратними сантиметрами. Квадратний сантиметр – це площа квадрата зі сторонами 1 см. Скорочено записують так: 1см², 7 см², 10 см²