Методичні рекомендації "Вдосконалення обчислювальних навичок на уроках математики в початковій школі".doc

        Управління освіти  Чернігівської міської ради

Чернігівська ЗОШ № 34

 

 

 

 

 

 

Шляхи вдосконалення обчислювальних навичок     молодших школярів

Вчитель-методист: В.О. Кондратюк

 

 

 

 

 

 

 

                                Чернігів, 2018

 

 

Кондратюк В.О.

Шляхи вдосконалення обчислювальних навичок молодших   школярів: Методичні рекомендації  для вчителів. – Чернігів, 2018

 

 

 

Навчально-методичний посібник  пропонує методику роботи на уроках математики для формування в учнів обчислювальних навичок. Підібрана така система вправ, яка спонукає учнів не просто обчислити приклад, а й вибрати для цього найбільш раціональний і доцільний спосіб розв’язання. Звертається увага на вироблення в учнів навички самоконтролю у процесі обчислень.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                        ВСТУП

 

Одним з головних завдань курсу математики в початкових класах є формування в учнів обчислювальних навичок.

Працюючи над цим питанням, я усвідомила , що на етапі формування обчислювальних навичок необхідно не тільки навчити учнів виконувати арифметичні дії з числами, а й навчити розв'язувати приклад різними способами, вибирати серед них найбільш раціональний і доцільний спосіб розв'язання, виробити в учнів навичку самоконтролю у процесі обчислень, навчити різним способам перевірки отриманого результату.

При цьому треба враховувати те, що учні мають різний рівень готовності до навчальної діяльності. Завдання вчителя - забезпечити для кожного з них оптимальний характер пізнавальної діяльності.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                            Зразки запису дій

Вже із самих перших кроків вивчення курсу математики знайомимо учнів із зразками запису дій.

По-перше, це зразки алгоритмів дій, які ілюструють прийоми усного чи письмового виконання арифметичних дій:

 

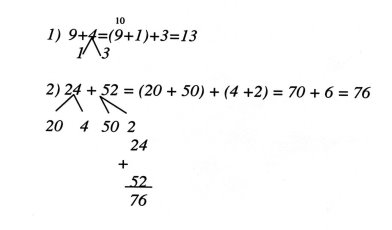
Використання зразка алгоритмів дій спирається на попередні знання й уміння учнів. Робота за зразком алгоритмів дій передбачає:

1) актуалізацію знань учнів;

2) повторення вивченого матеріалу;

3) аналіз зразка при поясненні і первинному закріпленні;

4) звернення уваги учнів на нові умови застосування знань.

         Під час порівняння зразків робимо узагальнення, яке вказує на більш раціональний шлях виконання дії для поданих чисел. Наприклад, вибираючи найбільш раціональний спосіб розв'язання, учні роблять висновок, що приклад

1283 х 5 - краще розв'язати письмово,                                                                                        а 1003 х 5 - способом розкладання 1003 - на розрядні доданки (усно).

Осмислення учнями алгоритму дії запобігає виникненню помилок під час обчислень, причиною яких є нерозуміння виконуваного запису, нерозуміння порядку обчислень.

          По-друге, даю зразки форм запису, використовуючи для цього демонстраційну наочність, пам'ятки. Якщо учень самостійно вміє вибрати форму запису, то це прискорює темп роботи на уроці.

 

 Зразки форм запису можуть бути такими:

 

1) Розклади на розрядні доданки:

     248 = 200 + 40 + 8

2) Заміни дію множення додаванням:

    3x5=3+3+3+3+3

3) Заміни числовий вираз рівноцінним:

    50 + 6 = 6 + 50

    (3 + 5)х6 = 3х6 + 5х6

    (7 - 2 ) х 5 = 7x5-2x5

4) З прикладу на додавання утвори два приклади на віднімання: 

    75+14=89                   

    89-75 =14

    89- 14=75

 5) Розв 'язок  рівняння записуй так:

     х +350 = 600

     х = 600 -350

     х = 250

   250 + 350 = 600       і т.п.

 

По-третє, щоб урізноманітнити роботу з удосконалення обчислювальних навичок, знайомлю учнів із зразками запису математичних завдань, поданих у нестандартному вигляді:

 

1)  збільш (зменш) на 7 число :   238, 48, 10006;

2)  продовж ряд чисел:         3 7 30 45 83 69

                                                10 14 37 52 ... ...

 

3) заповни таблицю:

 

а	а + 7	а х 7
38
42
56
102

 

4) доповни до 19:

 

19	1	2	5	6	8	10	12

 

5) обчислити:

 

доданок	100	300	800
доданок	20	400	300
сума

 

6)  розв’яжи ланцюжок:

 

    6 x 3 : 2 x 4 + 50 : 2

 

          1230: 2

           -600

           х 3

          + 60

           x 10

 

7) обчисли і постав знак   > ,    < чи = :

   832 x 2 ... 171 x 8

   625 + 600 - 300 ... 725 + 500 - 300

 

8) постав дужки так, щоб результат збільшився (зменшився) :

 

   600 – 320 : 4 x 2

 

10) математичні ігри на обчислення:

а) гра "Хто швидше? " (з'єднай приклад з відповіддю):

 

 

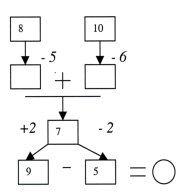
б) заповни клітинки , визнач перше число:

 

 

в) заповни фігури, отримавши числові вирази:

 

 

 

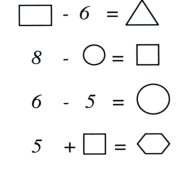
г) - Який інструмент потрібний столяру?

   Ножиці    - 7,  пилка - 4, лопата -8.

 

 

 

д) магічні квадрати:

5		15
24	14
	6	23

 

      Запобігання виникненню математичних помилок

 

У виробленні міцних обчислювальних навичок важливе значення має запобігання виникнення можливих математичних помилок та виправлення вже допущених.

Помилка - це не лише неправильна відповідь, а й певні порушення у розмірковуванні учнів. Різні причини помилок в обчисленнях зумовлюють неоднакову попереджувальну роботу. Важливо, щоб учень засвоїв сам прийом обчислень, диференціював різні способи обчислень, вибираючи серед них найбільш доцільний і раціональний.

Для ілюстрації утворення алгоритму обчислень і попередження виникнення можливих помилок розглянемо тему "Письмове віднімання багатоцифрових чисел."

З письмовим відніманням учні знайомляться у другому класі чотирирічної школи. З метою швидкого оволодіння алгоритмом письмового віднімання необхідно працювати у такій послідовності:

1)  засвоєння учнями складу чисел в межах 10 (І кл.);

2)  віднімання з переходом через десяток у межах 20 (І кл.);

3)  віднімання двоцифрових чисел без переходу через десяток,   з переходом через     десяток;

 

(При поясненні цієї теми застосовуємо демонстраційну наочність у вигляді таблиць - гармошок, за допомогою яких легко ілюструвати склад числа у вигляді розрядних доданків:

 

4 5  - 13  = 40 + 5 - 10-3  = 30 + 2 = 32

 

47 - 3  = 40 +  7-3  = 40 + 4 = 44

 

86 - 14  =  80 + 6 – 10 -4  =  70 + 2 = 72

 

А також картки із вказівкою прийому обчислень:

68-32=         або      45- 34 =      ).

 

 

     4) Коли засвоєний алгоритм усного віднімання , то пропоную записати ці ж приклади у стовпчик, пояснивши принцип запису:

       45                       47                        86

       -                         -                           -

       13                        3                         14

 

(На основі спостережень, особливо, виконуючи приклади, де є перехід через десяток, учні роблять висновок, що при усних обчисленнях спочатку дії виконуються з одиницями вищого розряду, а потім – нижчою. А при виконанні письмових дій - навпаки: спочатку дія віднімання виконується з одиницями нижчого розряду, а потім - вищих розрядів).

 

5) після засвоєння учнями дії письмового віднімання двоцифрових чисел - у III класі (у темі "Тисяча") робимо перенос цього алгоритму з двоцифрових чисел - на трицифрові:

 

  45                       145                        86                        386

  -                        -                          -                        -

  13                       113                        14                        214

 

6) а в IV класі (тема "Багатоцифрові числа" ) це й же алгоритм переносимо на багатоцифрові числа.

- Які ж помилки є найпоширенішими при письмовому відніманні?

 

80532            70000            8000            90000

_                  _                       _                   _

5486             23840             7356            24970

75046            46260            1644            66130

(неправильна

 форма запису)

 

Проаналізувавши ці помилки, можна зробити висновок, що причина їх - невміння замінювати одиницю вищого розряду одиницями нижчого розряду.

Тому для попередження цих помилок проводимо цілу систему вправ, які наочно демонструють віднімання з переходом через розряд:

 

1)  взяти з пучка у 100 паличок 1,2,3 палички

(учні бачать необхідність замінити 1 сотню 9 десятками і 10 одиницями);

 

2)   взяти з пучка у 100 паличок 1, 2 десятки

(учні бачать необхідність замінити 1 сотню 10 десятками);

 

3)  взяти з пучка у 100 паличок 1 десяток і 2 одиниці(учні бачать , що 1 сотню треба розкласти на 9 десятків і 10 одиниць);

 

4) аналогічно - взяти 3 одиниці з 5 сотень і т.п.

 

    Висновок, який повинні зробити учні на основі спостережень:

щоб відняти з декілька сотень десятки (одиниці), треба 1 сотню замінити 10 десятками ( 9 десятками і 10 одиницями).

 

 

Далі робота проводиться за вправами підручника:

1)  зменшити 100, 300, 700 на 1, на 2, на 3;

2)  яке число менше на 1, ніж 200; 700; 7000;

3)   зменшити на 5 одиниць , на 5 десятків, на 5сотень: 6000; 40000; 600000;

4)  обчислити:

1000 - 700 =

      1000 - 70 =

      1000 -  7=        і т.п.

 

Осмислення учнями алгоритму письмового віднімання знижує кількість помилок, тому навчаю дітей обчислення супроводжувати детальними поясненнями, потреба в яких поступово відпадає ( по мірі засвоєння алгоритму). Обов'язковий при виконанні дій - самоконтроль, а також - перевірка результату, про що піде мова нижче.

Другий вид обчислень, у якому учні роблять найбільше помилок, це - письмове ділення багатоцифрових чисел.

Проаналізувавши помилки при діленні багатоцифрових чисел, очевидні такі причини:

    1) невміння учнями свідомо з'ясовувати кількість цифр у частці;

    2)  неправильне уявлення учнів про те, що, якщо менше число не ділиться на більше число, то і частки у такому випадку немає;

    3)  формальне засвоєння способу утворення неповного діленого;

    4)  відсутність знання про те, що кожне неповне ділене обов'язково дає цифру у частці у відповідному розряді.

Знаючи причини помилок при письмовому діленні, при підготовчій роботі особливу увагу звертаю на ділення з остачею.

 

Розв'яжи:        62 : 8 — 7 (ост. 6)

                              /\

                         56 + 6

 

 

 

 

Пояснення:

       1) число 62 ділиться на 8 з остачею;

       2) без остачі ділиться найближче число 56;

      3) 56 ділимо на 8, получаємо частку 7;

      4)остача 6, остача менше дільника 8.

 

       Для засвоєння алгоритму ділення з остачею використовуємо  пам'ятку.

 

                                         Пам^’ятка

 

1)  Число         ділиться на          - з остачею.

 

2) Без остачі ділиться найближче число      .

 

3)        ділимо на       , получаємо     (пишемо частку).

 

4) Остача          , остача менше дільника.

 

5) Перевіряю себе: частку множу на дільник і додаю остачу - виходить ділене.

        Потім алгоритм ділення з остачею використовуємо при письмовому діленні багато цифрових чисел.

 

    Самоконтроль учнів під час виконання обчислень

 

     Крім попереджувальної роботи, яка запобігає виникненню помилок, необхідно ще навчити учня здійснювати самоконтроль при виконанні обчислень. Учням допоможе спланувати роботу і правильно виконати завдання:

       1)  коментоване розв'язування вправ;

       2)  робота за зразком ( за аналогією);

 

                                                                200        60       16

Зразок: 138 х 2 =(100 + 30 +8 )х 2= 100х 2 + 30х 2 + 8х 2 = 276

 

 

Виконай за зразком, проміжні дії виконуй усно:

 

                  125x3 =

                 234x2 =

                 415x2 =

                 112x5 =

 

       3) опорні схеми;

 

 Розв’яжи приклад, користуючись схемою:

 

             (+)   →     х    →      :      →       -      =

 

                983-(115+27)х6:2 =

 

          4) пам'ятки;

 

                                          Пам'ятка

         Ділення багатоцифрового числа на одноцифрове

 

1)  Прочитай і запиши приклад.

2)  Виділи перше неповне ділене.

3)  Визнач вищий розряд і кількість цифру частці.

4)  Поділи, щоб знайти цифру вищого розряду частки.

6)  Відніми їх, визнач остачу.

7)  Перевір, чи остача менше за дільник.

9)  Продовжуй ділення до кінця (аналогічно).

        10)  Перевір результат.

    5) диференціація завдань.

 

        Диференційовані завдання, враховуючи попередню підготовку учня, підбираю за двома принципами:

 

    1)  за ступенем самостійності (різна міра допомоги);

    2)  за ступенем складності (середній, достатній і творчий рівень).

        Диференціюючи завдання за ступенем самостійності, надаю різну міру допомоги. Для цього надається інформація такого виду:

 

     а) різна ступінь конкретизації завдань:

 

Середній рівень     .     - Які сторони у      прямокутника      мають однакову      довжину?   - Виміряй сторони      прямокутника.   - Знайди суму      сторін      прямокутника.

Достатній рівень     - Яка довжина      прямокутника?     - Яка ширина      прямокутника?     - Обчисли      периметр      прямокутника.

Високий рівень     - Знайди периметр      прямокутника.

 

    б) розв'язання допоміжних завдань , що приводить до розв'язання основного завдання:

 

 

 

 

 

Порівняй числові вирази:

 

384+168…285 + 275   384                   285 +                      + 168                    275 …52                 …60

384+168…285 +  275   384              285   +           +  168           275

384+168…285+ 275            +               +       ___           ___

 

 в) вказівка на прийом  розв’язання:

Розв’яжи приклади:

273+124=300+90+7=397 124 + 245 = 312 + 246 =

273 + 124 = 200 + 100 = 300  70 +   20 = 90    3 +    4  = 7 124 + 245 = 312 + 246 =

273      124          312  +          +             + 124      245          246 397

 

 г) навідні питання:

Розв’яжи рівняння:

- Як знайти невідомий додаток?

х+300=700        х+348=600

х=700-300       623+  х=800

х=400

400+300=700

    д) наочне підкріплення, пам’ятки:

        Розв’яжи вираз:

(+) →  х  →   :   →   -    =

1000 – (230 + 5 ) х 6 : 2 =

 

Поступове ускладнення завдань дає змогу учням по мірі засвоєння матеріалу переходити на більш високий рівень підготовки.

 

Перевірка правильності  результату обчислень

 

Але часто буває так, що учень вміє спланувати свою роботу , виконати завдання , а перевірити правильність результату - неспроможний. Самоконтролю дітей треба цілеспрямовано вчити вправляти у застосуванні різних його прийомів і способів.

 

 

Для цього застосовуємо такі види роботи:

      1)  взаємоперевірка ( у парах);

      2)  опитування (із здійсненням оперативного зворотного зв'язку за допомогою сигнальних карток "світлофорів" і т.п.);

      3)   самоперевірка за інструкцією;

 

         Наприклад, розрізаємо картинку на 4 частини. Із зворотного боку пишемо приклади. Учень розв'язує їх і накладає на контур, де вказані відповіді. Якщо получилося скласти картинку, то робота виконана правильно.

 

4. перевірка зворотною дією; аналогічною дією;

 

 

5.   виконання вправ на відшукання помилок, пояснення причин їх виникнення;

 

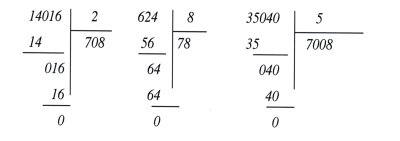
      6)  виконуємо один і той же приклад різними способами, відповідь повинна бути однаковою;

                                400          180            6

            293 х 2 = 200 x 2 + 90 x 2 + 3 x 2 = 586

            293  x2 = (300 - 7 ) х 2= 600 - 14 = 586

                                293

                              х   2    

                               586

6. даються готові відповіді для перевірки або відповіді зашифровані (для активізації роботи);

 

 

 

 

Дунай? Дніпро ? Десна ?

Відповіді: 1130 км, 2200 км, 2850 км.

Дніпро : 25368:4-2071 х2 =

Дунай : 10000 - 286x25 =

Десна : 23 х 14+101 х 8=

 

     8) прикидка результатів, неповна перевірка;

        Наприклад, не обчислюючи повністю, знайди помилку:

 

      х   4                  х   30                х   3

       732                    468                 775

 

При діленні - порівняння частки з дільником, діленим, обчислення кількості цифр у частці. При перевірці ділення з остачею - груба прикидка : множать останню цифру частки на останню цифру дільника і додають остачу, дивлячись, чи остання цифра діленого відповідає останній цифрі отриманого числа.

 

     9) обчислення і перевірка за допомогою мікрокалькулятора раніше отриманого результату.

         Самостійне виявлення допущених помилок з наступною роботою по їх виправленню сприяє не тільки якісному формуванню обчислювальних навичок, але й вихованню звички контролювати свою діяльність.

 

 

 

 

 

 

 

 

 

 

                          Використані джерела:

 

 

2. Богданович М., Менжунова Н. Зразки дій в початковому навчанні математики, - К., - ж. "Початкова школа", 2000, №2, с.9.

 

3. Логачевська С. Диференційоване навчання на уроках математики. - К., -ж. "Початкова школа" , 2001, №5, с. 18-22.

 

4.  Савченко О.Я. Дидактика початкової школи. – К.: Абрис, 2002.

 

5. Ресурси Інтернету.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                             ЗМІСТ

 

Вступ ……………………………………………………………… 3

 

Зразки запису дій ………………………………………………… 4

 

Запобігання виникненню математичних помилок …………….  9

 

Самоконтроль учнів під час виконання обчислень …………... 13

 

Перевірка правильності  результату обчислень ……………….17

 

Використані джерела.......………………………………………...20