Харківська спеціалізована  школа І-ІІІ ступенів № 85

Харківської міської ради  Харківської області

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИВЧЕННЯ   МАТЕМАТИКИ

В   СИСТЕМІ   РОЗВИВАЛЬНОГО   НАВЧАННЯ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Харків 2020

Харківська спеціалізована  школа І-ІІІ ступенів № 85

Харківської міської ради  Харківської області

 

 

 

Автор-упорядник: Чуєва Надія Прокопівна, вчитель початкових класів

                                 ХСШ № 85, спеціаліст вищої категорії, учитель-методист.

 

 

 

    Вивчення математики в системі розвивального навчання. – Харків, 2020. –36 с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

Вступ ...........................................................................................................................4                                                                                                           

1. Формування поняття числа...............................................................................6
   1.        Ознаки предметів. Порівняння предметів за різними ознаками.

       Величини..............................................................................................................6

1.2. Додавання й віднімання величин.......................................................................7

 1.3. Натуральне одноцифрове число........................................................................8

 1.4. Додавання й віднімання одноцифрових чисел.................................................9

 1.5. Багаторозрядне (позиційне, багатоцифрове) число.......................................10

 1.9. Звичайні дроби...................................................................................................13

2. Коментар до окремих розділів підручника “Математика, 2 клас”

Захарової Г. М....................................................................................................14

 2.1.Розділ I. Як вимірювати величину, якщо вона набагато більша за мірку?...16

 2.2. Розділ II. Як ще можна записати результат вимірювання?...........................19

 2.3. Розділ III. Якою може бути остача при вимірюванні додатковою мірою...20

Висновки....................................................................................................................22

Додатки.......................................................................................................................23

Список використаної літератури..............................................................................36

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

Головною метою навчання математики в системі розвивального навчання  Д.Б. Ельконіна – В.В. Давидова є формування в молодших школярів навчальної діяльності, яка спрямована на зміну нею себе як суб’єкта учіння. Можна виділити такі етапи навчальної діяльності: постановка навчальної задачі, пошук засобів і способів її розв’язання, саме розв’язання, контроль і оцінювання ходу і результатів роботи.  Суб’єктивність – це участь дитини разом з дорослими та іншими учнями у конструюванні та освоєнні способів дій. Завдання на конструювання і наступне опанування нового способу дій висуває сама дитина, оцінивши наявні способи як недостатні для подолання труднощів, що виникли, і прагнення цей недолік ліквідувати. 

Чому саме в цьому віці необхідно формувати навчальну діяльність?

Тому що кожному віку людини відповідає певний тип провідної діяльності:

1. Безпосередньо-емоційне спілкування характерне для дитини від народження до 1 року (формується потреба в спілкуванні з іншими людьми).
2. Предметно-маніпулятивна діяльність характерна для дитини від 1 до 3 років його життя (дитина відтворює суспільно вироблені  способи дії з речами).
3. Ігрова діяльність характерна для дитини від 3 до 6 років його життя (орієнтування на зміст людських відносин і дій).
4. Навчальна діяльність характерна для дитини від 6 до 10 років його життя (формується теоретичне мислення , розвивається рефлексія, аналіз, синтез, потреба і мотиви навчання).
5. Суспільно корисна діяльність характерна для дитини від 10 до 15 років його життя (потреба  у виконанні різних видів діяльності).
6. Навчально-професійна діяльність характерна для дитини від 15 до 17-18 років його життя (потреба працювати, самореалізуватись).

Навчальна задача – це задача на опанування узагальненого способу дій, яке можливе в процесі дослідницької діяльності учнів. Організація і розгортання такої діяльності перетворює дитину  в суб’єкт. Необхідною умовою будь-якого дослідження є співставлення результатів і шляхів їхнього отримання різними дослідниками, яке здійснюється у формі колективного навчального діалогу. Розвивальне навчання спирається на спільну діяльність учнів і вчителя.

 Теорія розвивального навчання обгрунтовує, що формування узагальнених способів дій можливе лише в результаті засвоєння молодшими школярами системи наукових понять. У програмі математики початкової школи таку систему формують поняття натурального одноцифрового числа, натурального багатоцифрового числа, дробового числа (звичайного дробу).    Формування наукових понять неможливе без оволодіння засобами дослідницької діяльності.

Відмінною особливістю вивчення математики є організація навчального матеріалу у вигляді системи математичних понять, які розгортаються послідовно.

Формування поняття числа передбачає знання дитиною вихідного для даного виду числа відношення величини і вміння виконувати арифметичні дії з цими числами.

Слід виділити такі змістовні лінії:

• Властивості й відношення предметів.
• Величини та одиниці вимірювання величин.
• Числа і дії над ними.
• Числові й буквені вирази.
• Розв’язування текстових задач.
• Геометричні фігури та їхні властивості. Геометричні тіла.
• Вимірювання геометричних величин і обчислення їхніх значень.

   Усі названі змістові лінії забезпечують розв’язання завдань вивчення математики в початковій школі, які визначені Державним стандартом початкової  загальної освіти.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Формування  поняття числа

 

1.        Ознаки предметів. Порівняння предметів за різними ознака­ми. 

          Величини.

 

Формування здатності успішно орієнтуватися в навколишній дійсності забезпечується великим обсягом практичних завдань на порівняння та зрівнювання предметів за різними ознаками на етапі “дочислового” періоду, а також на інших етапах навчання.

Формування поняття натурального і дробового числа забезпечується аналізом вихідного для всіх видів чисел відношення – відношення величин, тому вивчення математики в 1 класі розпочинається з вивчення величин. Відтворення величини дозволяє виявити походження числа і послідовно побудувати різні види чисел.

   На перших уроках математики діти виявляють, що під час розв'язування деяких практичних задач необхідно враховувати різні вла­стивості предметів.

    Математика для дитини розпочинається з виділення того боку навколишньої дійсності, який описується математичним поняттям величини.

   Діти вчаться практично порівнювати предмети за якоюсь озна­кою, вчаться практично порівнювати величини (довжину (ширину), масу, об'єм, кількість, площу). Через виконання практичних дій учні фор­мулюють способи порівняння величин (довжини – прикладанням (накладанням), сумістивши початки; площі - накладанням однієї фігури на іншу, пере­кроюючи одну з фігур; кількість - установленням взаємно однозначної відповідності; об'єм - переливаннями;

масу - за допомогою вагів).

    Задача відтворення величини  розв’язується безпосередньо зрівнюванням або опосередкованим практичним добором величин.

    Діючи з різними предметами, намагаючись замінити один предмет іншим, відповідним за якоюсь заданою ознакою, діти виділяють кількісні параметри речей, які є величинами, тобто власти­вості, для яких можна встановити відношення «рівно - нерівно», «більше -менше».

    Одним із напрямків курсу математики є опанування дітьми дії моделювання. Одна з перших моделей – два відрізки, які фіксують відношення рівності-нерівності. Пізніше це відношення моделюється формулами:

                           

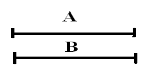
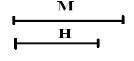
А=В                                                   M≠H

В=А                                                   М >Н

                                                           Н< М               

 

    У подальшому відношення нерівності конкретизується у відношення «більше-менше», що також фіксується відповідними формулами.

     Зрівнювання ве­личин за допомогою посередника приводить до обґрунтування властивості транзитивності рівності.

         А=В

         В=С

         А=С

Потім при неможливості безпосереднього її розв’язання, необхідно ввести новий спосіб зрівнювання, який приводить до необхідності ввести операції з величинами – додавання і віднімання та вивчення їх властивостей.

 

2.        Додавання й віднімання величин

 

Особливістю розвивального навчання є те, що відношення “дорівнює- не дорівнює”, “більше – менше”, а також дії додавання і віднімання з’являються та досліджуються на моделях у загальному вигляді ще до вивчення числа. Ці відношення фіксуються за допомогою моделі (схеми і формули у загальному вигляді).

        
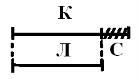
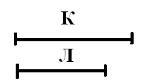
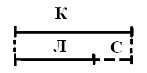
            К>Л                               Л<К                                              К>Л                              

            Л<К                               К-С=Л                                          Л+С=К                         

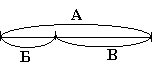
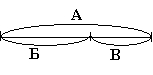
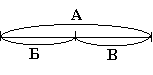     Ще один вид задач на  зрівнювання є відтворення величини шляхом додавання з використанням заздалегідь заданих частин (віднов­лення цілого за частинами).

   

 

 

 

                  А > Б

                  А > В

                  Б = В                                  Б < В                                       Б > В

 

 

 

Також розв'язується задача відновлення частини при наявності цілого і іншої частини, яка моделюється за допомогою рівняння. Трохи згодом рівняння фіксує і задачу на знаходження невідомого цілого.

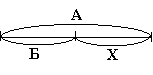
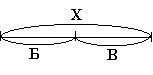
    Розв’язуються два види задач - на  знаходження невідомої частини і знаходження невідомого цілого. На­кресливши відповідну схему, дити­на легко може розв'язати перелічені задачі.

 

 

 

 

 

   Х – Б = В                 Х – В = Б                    Б + Х = А         А – Х = Б 

                       Х = Б + В                                            Х = А - Б

 

    Діти відкривають для себе переставний і спо­лучний закони додавання (вводяться назви законів), відношення між час­тинами і цілим («частина менша за ціле», «ціле більше за частину»), відношення між компонентами дій додавання і віднімання (терміни, що називають компоненти і результат  дії додавання, вводяться у 1 класі, а терміни, що називають компоненти і результат  дії віднімання, – у 2 класі).

 

 

1.3.Натуральне одноцифрове число  

 

       Для відтворення величини у  випадку, коли посередник використати неможливо, неможливо її звести до якогось із попередніх випадків, виникає необхідність пошуку нового способу розв'язання.

   У цьому випадку відбувається вимірювання величини частиною тієї ж  величини (довжини -  довжиною, площі - площею, об'єму - об'ємом, ...) відомим учням способом  і фіксації кожної дії міткою.

   Ускладнення умови задачі приводить до нового способу розв’язання – використання міри – та відношення до неї величини – числа. Число з’являється як результат дії вимірювання, як відношення величин.

   Тепер величину можна відтворити, використовуючи міру і число.

 

 

 О

 

 

е

 

    Після побудови графічної моделі дії вимірювання вводиться і знакова модель, яка фіксує відношення величини до міри - формула.

      Читається формула так: «У величині О міститься 7 мір е» або «О за мірою е дорівнює 7».

   Дещо пізніше , коли дітям уже ві­домі та зрозумілі основні властивості числового ряду, вони починають по­значати числа арабськими цифрами:

1, 2, 3, 4, 5, 6, 7, 8, 9.

   Графічне моделювання дії вимірювання-відмірювання приводить до побудови особливого виду моделі — числової прямої. На прямій позна­чається точка II (початок вимірювання-відмірювання), і від цієї точки відкладаються послідовно в одному напрямку (довільно вибраному) рівні відрізки (міри). Після кожного відкладання міри біля отриманої точки на прямій ставиться відповідний знак числового ряду.

 

 

 

     Числова пряма дає можливість раціональніше розв'язувати вже відомі задачі порівняння, додавання, віднімання величин, виконуючи тепер уже дії з числами, а не з величинами.

     Тепер для порівняння величин вистачить їх виміряти і порівняти числові значення - результати вимірювання відповідних величин.

 

 

 

7>3

 

1.4.Додавання й віднімання одноцифрових чисел

 

   Додавання величин можна замінити додаван­ням чисел на числовій прямій, замінивши суму результатів вимірювання двох величин одним числом - її числовим значенням. Ця задача розв'язується на числовій прямій способом прилічування .

 

 

 

       7 + 2 = 9

   Одним із завдань навчання є формування обчислювальних навичок.

    Перша обчислювальна задача в курсі математики: заміна суми чисел одним числом - числовим значенням суми .

   Дія віднімання чисел вводиться аналогічно дії додавання. Віднімання величин можна замінити відніманням чисел на числовій прямій, замінивши різницю результатів вимірювання двох величин одним числом -  числовим значенням різниці. Ця задача розв'язується на числовій прямій способом «відлічування» .

 

 

 

 

       7 – 2 = 5

 

1.5.Багаторозрядне (позиційне, багатоцифрове) число

 

    Іноді величина вияв­ляється настільки більшою від вибраної міри, що використання початкової міри стає нераціональним . За такого співвідношення величини і міри сам процес вимірювання стає занадто довгим, а для запису результату до­водиться будувати дуже довгий ряд одноцифрових чисел, вигадуючи для цього дедалі нові знаки.  Виходом із цієї ситуації є вибір іншої, більшої міри. Але для визначення відношення величини до вихідної міри необхідно встановити і відношення «нової» (більшої) міри е₂ до «старої» (малої) е₁. Таким чином, нова міра е₂ використовується як додаткова, а результат вимірювання фіксується не одним числом, як у попередньому випадку, а парою чисел, одне з яких є відношенням додаткової міри  е₂ до ви­хідної е₁, а друге - відношення величини до додаткової міри е₂. Тобто резуль­тат вимірювання можно зафіксувати парою формул:

                                                                                                               

               

 

                        

 

С

 

 

           e1

 

 е2

 

      

 

  ;       .     

          Такий запис приводить до необхідності ввести іншу форму запису - числовий вираз (пара чисел, з'єднаних крапкою). Вираз на цьому етапі означає лише опис виконаної дії: зміна вихідної міри е₁ і використання нової міри е₂ під час вимірювання величини (наприклад, «По п’ять узяти (повторити, відкласти) три рази»). У подальшому, в третьому класі, результат вимірювання величини за допомогою додаткової міри приведе до введен­ня дії множення.

 

           ·  3

 

     Результат вимірювання за допомогою додаткової міри е₂ можна записа­ти ще в інших формах: у вигляді таблиці, у вигляді позиційної форми. Усі форми фіксації дії вимірювання взаємно пов'язані і перетворюються одна на іншу.

   Згодом з'являється необхідність позначити «порожній» розряд у по­зиційному записі (коли в таблиці залишилося вільне місце, тобто під час вимірювання якась міра не працювала). Для цього використо­вується цифра «нуль».

   У випадку ще більшої різниці між величиною і вихідною мірою бу­дується не одна додаткова міра, а система мір з постійним відношенням між ними. Оскільки результат вимірювання кожною мірою фіксується ок­ремим числом, виникає необхідність знайти раціональний і зручний запис результату вимірювання. Такою формою запису є розрядна таблиця і по­зиційне число, у якому результат вимірювання кожною окремою мірою стоїть у певній позиції (місці), а значення кожного знака і віднесеність йо­го до певної міри визначаються його місцем у послідовності знаків. (Набір формул і числовий вираз стають занадто громіздкими і незручними для запису  результату вимірювання системою мір.)

   Використання розрядної таблиці дозволяє дитині самостійно проконтролювати наявність чисел у розрядах і не припускатися помилок у записі позиційних чисел (наприклад, у випадку, коли в деяких розрядах стоїть «нуль»), а також конструювати способи виконання дій з багатоцифровими числами.

     Відношення між мірами (основа системи мір) установлюється довільно, і запис результату вимірювання набуває форми позиційного чис­ла у відповідній до вибраної основи системі числення. Числа в недесяткових системах числення діти читають, послідовно називаючи розрядні чис­ла, починаючи з найвищого розряду і вказуючи основу системи числення. Наприклад:

211      -«Два  один  один у п'ятірковій системі числення».

 

34 -«Три чотири  у п'ятірковій системі числення».

 

30 -«Три нуль  у п'ятірковій системі числення», або

 

34 -«Три чотири  основа системи п'ять».

 

 

Відтворення величини, коли вона виявляється набагато більшою від вибраної міри, приводить до появи додаткової, більшої міри, а згодом і системи мір з постійним відношенням між ними. Розв’язання цієї задачі приводить до появи багатоцифрового числа. Результат вимірювання записується в різних системах числення (відповідно до основи системи мір).

 

 

                                                                                                               

               

 

                        

 

С

 

 

 

           e1

 

 е2

       

 

                             ·  3 + 4 = 34

 

 

 

 

 

Р
 

 

е1

 

е2

 

е3	е2	е1
ІІІ	ІІ	І
2	1	1	211
	3	4	34
	3	0	30
		7	7

е3 

 

                                                   
 

     Десяткова система числення розглядається як поодинокий випадок.

     Назви для десяткових чисел вводяться в міру появи чисел (спочатку дво­цифрові в межах 100, а потім багатоцифрові в ме­жах мільярда (2 клас).

   Єдиний принцип побудови різних систем числення наочно підтверджується, коли числа в різних системах числення записуються у вигляді суми розрядних доданків:

211  =200        + 10        +1

 

211 = 200  +  10  +  1

 

1.6. Звичайні дроби

 

   Коли необхідно відтворити величину, меншу від стандартної міри, виникає потреба роздробити (зменшити) основну міру.

   Початкова міра ділиться на рівні частини таким чином, щоб одна така части­на укладалася у величині ціле число разів. У цьому випадку результат вимірювання фіксується парою чисел, одне з яких указує на зміну міри (знаменник), а друге - на результат вимірювання новою мірою (чисель­ник).

Результат вимірювання фіксується у вигляді звичайного дробу (4 клас).

 

 

 

 е1                                                      

 

 

                                              

 

 

  e2

 
     

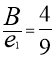
Усе коло питань, що пов'язані з цим новим числом, уже добре відоме дітям:

• необхідно знайти місце для нових чисел на числовій прямій;
• за допомогою числової прямої можна встановити відношення між числами;
• потрібно знайти способи дій із дробовими чис­лами.

 

 

 

 

 

2. Коментар до окремих розділів підручника «Математика, 2 клас»

 

Основною метою програми математики є поняття раціонального числа. Починається курс математики  з вивчення величин і властивостей їхніх  відносин , де наскрізною дією є відтворення величини.

Якщо в найпростішому випадку задача відтворення величини спочатку вирішується безпосереднім  урівнюванням, потім при неможливості безпосереднього її рішення вимагає введення посередника, то в наслідку доводиться ввести новий спосіб урівнювання, що приводить до необхідності введення операцій з величинами - додавання й  віднімання, до вивчення їхніх властивостей. Таким чином,  число з'являється як результат дії виміру, як відношення величин.

На наступному етапі логічно виникає розв'язання  цієї ж задачі  в  ситуації, коли величина виявляється настільки більше обраної стандартної міри,  що використання останньої  стає  нераціональним. Природним виходом із цієї ситуації  стає вибір іншої,  більшої міри, що вибирається  довільно. Таким чином, знову обрана міра використовується   як додаткова, а  результат виміру фіксується  вже парою чисел, одне з яких є відношенням додаткового заходу до вихідного,  а інше - відношенням величини до додаткової міри. А якщо виникає остача, то результат виміру фіксується вже трьома  числами. У випадку ще більшого розходження між величиною й вихідною мірою будується система мір з постійним відношенням між ними. Раціональним, зручним записом результату виміру є позиційне число. Оскільки відношення між мірами (підстава системи мір) встановлюється довільно, запис результату виміру здобуває форму позиційного числа в різних системах числення.

Десяткова система числення розглядається як окремий випадок.

Метою цього етапу математики є виділення принципів побудови багатозначного, позиційного числа, введення спеціальних форм фіксації результату виміру величини ( сукупність формул, числове вираження, таблиця й позиційна форма) .

Відношення між величинами і їхньою властивостю з найпершого етапу роботи фіксується  у  вигляді моделей. Одна з перших моделей - два відрізки які фіксують відношення рівності-нерівності. Пізніше це відношення моделюється формулами:   А = В,   А = С.

При розв'язанні задачі відтворення величини за допомогою міри  результат виміру (натуральне однозначне число) фіксується спеціальним знаком - цифрою. Дія виміру моделюється набором упорядкованих  знаків, розташовуваних на прямій на однаковій відстані одне від одного. Так з'являється числова пряма як модель дії вимірювання.                                                

  При вимірюванні величини за допомогою додаткового заходу потрібні інші форми  знакового моделювання ,одного числа, як у попередньому випадку, недостатньо:

-  сукупність двох або трьох  формул;

-  числовий вираз;

-  таблиця;

-  позиційне число.

Розділи підручника присвячені різним видам моделювання, їхньому  засвоєнню й перетворенню одних моделей в інші.                         

Вивчення   матеріалу  ділиться на два етапи:

1)   введення й робота з додатковою міркою;

2)  введення системи мір, моделювання різних систем числення й десяткова  система як окремий випадок;

3)  порівняння, додавання, віднімання багатозначних чисел.             

У даний посібник включені три розділи:

1) основні цілі й задачі першої частини математики для 2-го класу;

2)  рекомендації щодо  організації навчання ( приклади постановочних задач, уроків на відпрацьовування матеріалу, самостійних робіт).

3)  форми й види робіт на уроці.

Матеріали для вчителя являють собою коментарі з організації  навчальної роботи.

 

2.1.  Розділ I

Як виміряти величину, якщо вона набагато більша за мірку?

 

Зміст розділу.

- Вимір і рахунок за допомогою додаткової мірки.

- Запис результату виміру формулами.

- Побудова величини по заданій мірці й формулах.

 

Навчальні задачі.

1. Необхідність введення е, коли А >> е.

2. Запис результату

3. Побудова, вимір величини.

4. Запис результату виміру ( математична модель - формули).

5. Повна характеристика величини через 3 відношення

 

6. Розв'язувані й нерозв'язувані задачі. Контроль (аналіз умов, необхідних для побудови величини).

Навчальна діяльність на уроці організується у вигляді розв’язання наступних видів завдань:

- постановочні (дослідження),

- тренувальні (оцінні),

- для контролю.

Оцінні завдання зустрічаються на початку й наприкінці уроку. Їх мета встановити:

- що робили?

- чи  робили таке раніше?

-  чому навчилися:

1. Для реалізації постановочної задачі можливий такий сюжет

(дивись підручник,  № 12).

Устаткування:

У вчителя - 3 мотузки по 4см , мотузка - 32 см , мотузка – 160 см.

У груп дітей - моток шнура, шнур на 4см .

Завдання 1: У мене в руках шматочок шнура з якого роблять петельку для дитячого плаття. На одну петлю йде от стільки (показую шнур довжиною 4см).У вас на столах теж є зразок петлі й моток шнура.

Відріжте таку частину шнура, з якої можна зробити стільки ж петель, скільки в мене. Що для цього треба знати?

-(Д) -Необхідно виміряти довжину вашого шнура міркою (одна петля) і назвати число, тоді ми й відміряємо по числу й мірці.

-(У)-От,...(ім'я дитини), завжди в нас працює швидко, я думаю, що він і це завдання виконає дуже швидко і ми зараз довідаємося скільки "петель" міститься в моєму шнурі, тобі 1хвилина. Вистачить? Час пішов.(Дитина вимірює, не встигає) Працював швидко? Правильно?

-Чому ж не вдалося учням швидко виконати це завдання?

-(Д)- Маленька мірка, величина більша.

-(У)- А що ж раніше ми не працювали з маленькими мірками,навіть ще з меншими?

-(Д)- Величина більша.

-(У) Ми не працювали з більшими величинами? У чому справа: мірка маленька або величина більша?

-(Д)- Мірка маленька для цієї величини. Мірка набагато менша величини: А е

-(У)- Значить ось у чому причина затримки. Вимірювати незручно, довго. Як же прискорити процес виміру?

-(Д)- Треба взяти більшу мірку.

(Учитель дає дітям шнур на 32см)

-(У)- Цією міркою вимірюєте швидше? (Вимірює один учень біля дошки).Вийшло 5 таких мірок у величині. Тепер і ви відріжте від мотка стільки ж.

-(Д) - Ми не можемо цього зробити. У нас є тільки маленька мірка, а великої немає.

-(У)- Що ж робити? У мене вона одна. Я не можу віддати її відразу всім групам? Як же вам зробити самим таку ж?

-(Д)- Виміряти її маленькою міркою. (Відбувається вимір). У великій мірці 8 маленьких мірок. - Тепер у вас усе є для виконання завдання?

 Висновок:

1) А >> e₁

 

2)  

 

                                                                  A

 

-Що ж ми робили? Що позначають числа 8, 5?

-Чому знадобилася мірка е₂ ?

 

Завдання 2. Робота в парах

 

O	O	O	O	O	O
O	O	O	O	O	O
O	O	O	O	O	O
O	O	O	O	O	O
O	O	O	O	O	O

 

 

Зможете відрахувати потрібну кількість ґудзиків ? Як будете рахувати?

 

Підсумок.

- Що робили? Чому знадобилася е?

 

2. Наступна група завдань спрямована на відпрацьовування побудови й виміру величин (№4-7). Робота може бути організована в групах, парах, колективно й індивідуально. Залежно від форм роботи, учні працюють як з підручником (індивідуально, у парах, групах), так і по сюжетах, запропонованих вчителем (колективно, у парах).

Мета завдань:

-  виділяти додаткову мірку й користуватися нею;

- учити давати повну характеристику побудови й виміру величини при використанні е .

3. Завдання № 4-7 пропонують фіксацію результату виміру величини у вигляді математичних моделей - формул. Робота в класі за завданням № 9 може бути організована в такий спосіб.

Гноми Руді і Дитрих вирішили зробити подарунки бабусі Варварі й іншим своїм друзям. Ось такий килимок, (зразок на дошці). Вони приготували матеріал, але на всіх не вистачило, і більше матеріалу в них немає. Руді просить вас допомогти їм. Щоб кожна група виготовила от такий килимок.

- Ви можете це зробити ? (Ні).

- Чому? (Потрібно виміряти).

- Що вам потрібно для цього? (Мірка е).

- У вас на партах, у кожної групи є зразок килимка й мірка е .Вимірюйте. Працювати потрібно швидко, дружно. Чи все у вас є для роботи? Перевірте.

- Якщо ще щось потрібно, виготовте самі.

 

 

I

 

II

 

III

 

- Чи можна так записати результат виміру? (Так).

- А чи раціонально?

Обговорення результатів:

- Чи виконували ми таке завдання раніше?

- Ви вимірювали ту саму величину?

- Чому ж різні результати виміру?

- Звідки виникло третє число?

- Про що воно розповідає?

- Чому не вимірювали міркою е₁ ?

- Так яка остача? (Менше е₂).

- Чи можна відкинути остачу?

- Якою міркою вимірюється остача?

(Після обговорення на дошці фіксується результат з докладним коментарем) 

I

 

II

 

III

 

Наступне завдання спрямоване на з'ясування ступеня розуміння вивченого матеріалу. Завдання дається для роботи в групах.

Завдання: Сьогодні я одержала від учнів 2б класу записку.

Вони на уроці математики вимірювали величину, а результати виміру передали нам:

                e₁

 

- Число, що розповідає про остачу ви повинні вписати самостійно.

- Зможете побудувати величину? Дійте. (Групи, попрацювавши самостійно, зображують свою величину на дошці. Необхідно розглядати всі можливі варіанти величини з остачею й без неї).

 

Підсумок

-  Про що розповідає формула?

- Якою може бути остача?

 

4. Завдання 12,13 дозволяє дітям виділити достатність даних для побудови величин за допомогою е₂ . № 12 необхідно розглянути фронтально з детальним обговоренням. А робота над № 13 може бути організована у вигляді групової, парної, індивідуальної роботи на розсуд учителя.

5. Для контролю доречно використати завдання № 13, 14,15.

№ 13 - перш ніж побудувати величину, необхідно виміряти й записати результат виміру у вигляді формул, замалювавши обрані мірки.

№ 14 - побудова величини.                                                                               

№ 15 - складання дітьми перевірочних завдань для товариша, де

необхідно вимірювати або рахувати за допомогою додаткової мірки.

 

2.2.   Розділ II

Як ще  можна записати результат вимірювання?

 

Зміст розділу

-Запис результату виміру й рахунку за допомогою числового виразу й побудова величини за заданим числовим виразом.

Навчальні задачі:

1. Вступна задача: введення нової математичної моделі - числового виразу.

2. Різні    записи результату виміру: перехід від формул до числового виразу й навпаки.

3. Побудова величини за числовим виразом й вимір їх з наступним записом числового виразу,

4. Наступне й попереднє числа у вигляді числового виразу, їхнє утворення.

5. Числова пряма. Позначення за допомогою числового виразу крапок на числовій прямій.

6. Порівнювання чисел, заданих у    числовому виразі.

Нижче додаються поурочні розробки з даної теми.

2.3.   Розділ III

Якою може бути остача при вимірюванні  додатковою міркою?

 

Зміст розділу.

- Співвідношення остачі й  міри.

 

Навчальні задачі

1.Введення поняття остачі (основні характеристики остачі).

2. Оцінка числової характеристики остачі.

3. Вибір співвідношення числових характеристик міри й остачі,

4. Виділення можливих варіантів розв'язання задач з остачею.

 

    Зразковий сюжет постановочної задачі (№ 13).

Задача. Показав гном Руді своїм друзям нову шовкову краватку, що він пошив. Дитріх, Матті та Кріс захотіли мати такі ж. У Руді не було більше тканини, й гноми вирішили купити собі самі (Учитель прикріплює до дошки різнобарвні смужки, що відповідають тканині, придбаній гномами, й зразок краватки Руді).

 

 

 

 

 

 

Розв'язок

1)  Коли гноми прийшли за своїми краватками, Руді  уже все зробив.

Дитріху й Матті вийшло по одній краватці, а Крису - дві. (Зразки краваток прикріплені до дошки).

   Дитріх і Матті розсердилися на нього й сказали, що це нечесно, несправедливо. - У тебе ж залишилися шматочки нашого шовку.

 Чи згодні ви із цим? Що ви скажете? (Діти обґрунтовують свої відповіді, працюючи зі зразками тканини й краваток). 2)

- Якою міркою користувався Руді?

-Якою може бути остача?

-Обґрунтуйте свої відповіді, ост. < е₂

   Для закріплення можна використати матеріал підручника № 14,15.  № 14 виконується колективно, а № 15-самостійно з наступною перевіркою.

Наступна серія завдань спрямована на формування оцінки числової характеристики остачі № 17, 18.

 

 Можлива парна й групова форма роботи.

Завдання № 20, 21 спрямовані на відпрацьовування сформованості оцінки числової характеристики остачі. Робота ведеться в парах.

Підсумком роботи із цього розділу можна вважати самостійне розв’язання задач .

     Аня й Катя зібрали 7 букетів ромашок. У кожному букеті було по 5 квітів, і ще залишилися ромашки, з яких не вдалося зробити букет.

Скільки квітів залишилося на грядці? Скільки квітів могло залишитися на грядці?

Скільки квітів могло рости на грядці?

Запиши всі можливі числові вирази.

Розв'язок

 

 

 

              · 7+1

 

              · 7+2

 

              · 7+3

 

              · 7+4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

 

         Формування поняття числа неможливе без формування стійких обчислювальних навичок. Слід виділити дві складові будь-якої обчислювальної дії – алгоритм і дії з одноцифровими числами (таблиці додавання і множення).

Відношення величини і міри, тобто число, фіксується спеціальним знаком – цифрою. При цьому дія вимірювання моделюється числовою прямою. Число і числова пряма дають можливість більш раціонально розв’язувати вже відомі задачі.

Побудова понять величини й числа вимагає постійної роботи з різного виду моделями: схемами, формулами, рівняннями, таблицями, числовими і буквенними виразами та інші.

    Велика увага приділяється розв’язанню задач (їх розв’язання – це послідовне перетворення моделей, перехід від одного типу моделей до іншого).

Уявлення про основні геометричні фігури і тіла , початковий досвід вимірювання і обчислення геометричних величин, а також вироблення необхідних графічних умінь відбувається протягом усіх років навчання, починаючи з “дочислового” періоду і закінчуючи спеціальним розділом “Вимірювання і обчислення площ плоских фігур”.

Учні вміють пояснювати свої дії, логічно висловлюватись, доречно використовувати математичні терміни, доводити правильність власної думки в ході навчальної дискусії, діалогу.

Зміст, методи та  форми організації навчання в системі розвивального навчання орієнтовані на забезпечення кожному учню оптимальних умов для розвитку як суб’єкта, що сам змінюється. Основою концепції є любов і повага до дитини, яка стоїть в центрі педагогічної системи, звернення до  її внутрішнього світу, опори на її сили, внутрішній потенціал, підтримка і розвиток того здорового, що є в кожній особистості.

 Така система роботи дозволяє реально здійснювати педагогіку співробітництва, створювати сприятливий психологічний мікроклімат. Для педагогів школи важлива думка  автора системи В.В.Давидова :

“Важливо дати дитині не знання, а спосіб їх здобуття”.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

2 клас                                       Уроки математики

Урок 1

 

Тема уроку. Запис результату вимірювання і рахунку за допомогою                   

                     числового виразу.

Мета уроку. Знайти новий спосіб фіксації результату вимірювання величини у 

                     вигляді числового виразу. Розвивати пам'ять,логічне мислення.

                     Виховувати старанність, увагу, доброзичливі стосунки.

Обладнання уроку. Картки для груп учнів, підручник математики.

Хід уроку

1. Організація класу.
2. Актуалізація знань учнів.
   • Починаємо працювати.
   • Що треба зробити ? (Побудувати величину.)
   • Що допоможе вам її побудувати? (Формули та мірка е – початкова.)
   • Прочитайте першу формулу. Про що вона розповідає? (У величині мірку е відклали 4 рази.)

                            

 

 

 

•      Про що розповідає друга формула? Третя формула?
•      Формулу я вам дала , початкову мірку дала. Побудуйте величину.
•      Побудували величину? Я думаю, що величини у всіх однакові. (Ні.)
•      А чому? (Не визначили, яке число розповідає про остачу.)
•      Яке число розповідає про остачу?
•      Так, що число може бути будь-яке? ( 10, 25, 100, ...  .)  (Ні.)
•      Якою може бути остача? ( Менше 7 .)
•      Чому?
•      Як ви думаєте, у кого буде найбільша величина? ( Остача 6.)
•      А найменша? (Остача 0.)
•      Чи знайдемо в класі дві однакові величини?
•      У кого?
•      Величини однакові , а за якою ознакою?
•      Молодці! Хто задоволений своєю роботою?

3. Вивчення нового матеріалу.
   1. Повідомлення теми уроку
   •      Цікаво працювати з величинами? Сьогодні ми продовжимо цю роботу.

2. Постановка навчальної задачі.

Вимірювання величини – побудова величини.

Завдання.  Побудуйте в зошиті фігуру, в якій стільки ж клітинок, 

                  скільки квадратів в моїй фігурі.

•      Щоб побудувати таку величину, що треба зробити? ( Виміряти дану.)
•      Як виміряти? (Треба вибрати мірку е.)
•      Вибираєте мірку е, домовляєтесь. Яка?
•      Що можемо сказати про мірку і про величину?
•      Будемо вимірювати величину?

 

•      Чому?
•      Що треба зробити? ( Потрібно використати нову мірку.)
•      Яку?

 

 

 

 

- Якою міркою ми виміряємо величину швидше?

•      Була початкова мірка  е.
•      Що ми з нею зробили? (Збільшили.)
•      У скільки разів? (В 5 разів.)
•      Як це записати?  
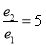
•      Побудуйте додаткову мірку.
•      Що робимо далі? (Вимірюємо величину міркою е.)
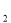
•      Запишіть результат вимірювання формулою. 
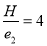
•      Всю величину виміряли?
•      Працює мірка е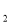? Чому?
•      Яка мірка виходить на роботу? ( е)
•      Виміряйте величину і запишіть результат вимірювання. ( )
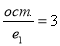•      Побудуйте.
•      Побудували? Таку ж? За якою ознакою?
•      А величини у нас однакові?

                                

 

 

 

 

 

•      Діти, результати вимірювання ми записали формулами. Вам зрозумілі ці формули? Але вони складні і зрозумілі не всім. Давайте запишемо їх інакше, щоб були зрозумілі всім. Адже математика наука точна, працюємо з числами.
•      В результаті вимірювання ми отримали три числа: по 5 взяти 4 рази та ще 3.
•      5  · 4+ 3    -   це числовий вираз.
•      Так записують в математиці?
•      Ми можемо придумати свої знаки, але тоді нас більше ніхто не зрозуміє. Ще до нас люди домовились записувати так.
•      Прочитайте.
•      Про що розповідають числа 5?  4 ? 3 ?

 

Висновок.  – Що вчилися робити на уроці? Як?

IV. Закріплення вивченого матеріалу.

1. Робота в парах.
   •      Давайте потренуємося записувати числові вирази та читати їх.

С. 25 , № 9(а, б, в).

2. Робота в групах.
   •      Задача № 10 (а).

V. Підсумок уроку.

•      Чому навчилися?
•      А будувати величини за числовими виразами – це задача на завтра.

Урок 2 – 3

 

Тема уроку. Побудова та вимірювання величин за числовим виразом.

                     Мета уроку.Вчити дітей будувати величини за числовими виразами,  

                                         вимірювати величини і записувати результат вимірювання

                                         числовим виразом і у вигляді формули.  Розвивати пам'ять, логічне

                                         мислення. Виховувати старанність, увагу, доброзичливі стосунки.

Обладнання уроку. Картки для груп учнів, підручник математики.

 

Хід уроку.

I. Організація класу.

II. Актуалізація знань учнів.

7  · 2 + 3      

- Що записано на дошці? Прочитайте. Про що розповідає кожне число?                      

-  Як інакше можна це записати?

- Побудуйте величину. Що вам для цього необхідно? ( е)

•      Які величини отримали? Чому?

III.Вивчення нового матеріалу.

1. Постановка навчальної задачі.

Робота в парах.

Задача. Визначте місце, де закопали клад, якщо на карті позначено: точка відліку, напрямок руху, числовий вираз, про кількість кроків, мірка е.

Обговорення.  Як діяли? Що отримали? Чи в одному місці зарито клад у всіх? Чому?

2.Робота в групах.

 

 

Учні працюють в групах з картками – схемами. Результат вимірювання фіксують в зошитах і на дошці (кожна група окремо).

Обговорення.

•      Що нового можете сказати про числові вирази?
•      Які вони?
•      Чому так вийшло, величина  у всіх груп було однакова?

Висновок. Результати вимірювання різні, тому що мірка е побудована

                  по-різному.

IV. Закріплення вивченого матеріалу.

1.Робота в парах.

1) Завдання для вимірювання величин і запис результату вимірювання числовим виразом: №13, 14.

2) Завдання на побудову величин: № 10 (б,в,г).

V. Підсумок уроку.

- Як можна записати результат вимірювання?

- Про що розповідає кожне число в числовому виразі?

Урок 4

 

Тема уроку. Перехід від формул до числових виразів.

Мета уроку. Відпрацьовувати вміння співставляти числа у формулах і числових виразах. Вчити використовувати нову форму запису результату вимірювання. Розвивати пам'ять, логічне мислення.                      Виховувати старанність, увагу, доброзичливі стосунки.

Обладнання уроку. Картки для груп учнів, підручник математики.

 

Хід уроку.

 

I. Організація класу.

II. Актуалізація знань учнів.

1. Задача. У Буратіно зберегалась записка про кількість монет, які він закопав. Записав він так:  8   · 2 + 7 .

 - Чи можете ви замалювати скільки монет закопав Буратіно? (Мірку е спеціально не обговорювати , і те як  закопувались монети.)

2. Завдання для вимірювання величини  № 31.

III. Вивчення нового матеріалу.

1. Постановка навчальної задачі. (Можливий сюжет.)

   Гноми допомагали бабусі Варварі на городі: поливала помідори і перець. Коли закінчила роботу, бабуся запитала у них про кількість відер води, які приніс кожен із гномів.

   Гноми свої відповіді записали так:

Руді:

Дитрих:

- Прочитайте ці записи. Про що  розповідає кожне число? Чи можете ви сказати, хто приніс більше води? (Пояснення дітей.)

-Запишіть результати за допомогою числових виразів.( Якщо у дітей виникає проблема порівняння числових виразів, дітям пропонується побудувати величини.)

3. Завдання на співвідношення числових виразів і формул № 14.

IV. Закріплення вивченого матеріалу.

1. Самостійна робота № 15.

V. Підсумок уроку.

•      Як ви можете записати результат вимірювання величин?

 

 

                            

 

 

 

Урок 5

 

Тема уроку. Зображення  числового виразу на числовій прямій.

Мета уроку.Формувати вміння визначати місце числового виразу на числовій

                     прямій. Розвивати пам'ять,логічне мислення.

                     Виховувати старанність, увагу, доброзичливі стосунки.

 Обладнання уроку. Картки для груп учнів, підручник математики.

Хід уроку.

I. Організація класу.

II. Актуалізація знань учнів.

1. Визначте на числовій прямій місце числових виразів.

 

0

 

 

 

•      Що зображено на дошці? Обгрунтуйте свої відповіді.
•      Що зображуємо на числовій прямій? (Числа.)
•      А можете ви позначити на числовій прямій числові вирази?

2. Доповніть записи, які числові вирази живуть в точках А, Б.

5  · 1 + 2                5  · 3

III. Вивчення нового матеріалу.

1. Постановка навчальної задачі. 

с.41, № 16 (а)

6  ·3+3

 Мальвіна попросила Буратіно та П'єро розставити вздовж доріжки від будинку до хвіртки стовпчики і розвісити на них ліхтарики, щоб увечері біля будинку було видно. Ліхтари­ки мусять висіти через кожні 6 кроків. На схемі Мальвіна показала першу мірку (крок), місце для першого ліхтарика і записала числовий вираз. Буратіно і П'єро мусять самі знайти місця для решти ліхтариків і викопати там ямки для стовп­чиків.

- Покажи на схемі, де повинна стояти решта стовп­чиків.

- Ти ж пам'ятаєш -  їх треба розставити через кожні 6 кроків.

- Запиши числовий вираз для кожного місця, де буде стовпчик з ліхтариком.

-Запис зроби під точками на кресленні так, як це зробила Мальвіна.

IV. Закріплення вивченого матеріалу.

1. Робота в парах. c.42, №16 (б, в, г)

Знайти на числовій прямій місце для числових виразів.

2. Колективна робота.  c.44, № 17

Знайти і записати рівні вирази.

3. Самостійна робота .  с.48, № 18

V. Підсумок уроку.

- Що нового дізналися на уроці?

  Урок 6

 

Тема уроку. Зображення  числового виразу на числовій прямій.

Мета уроку.Закріпити  вміння визначати місце числового виразу на числовій

                     прямій. Розвивати пам'ять,логічне мислення.

                     Виховувати старанність, увагу, доброзичливі стосунки.

Обладнання уроку. Картки для груп учнів, підручник математики.

 

Хід уроку.

 

I. Організація класу.

II. Актуалізація знань учнів.

1. Завдання на порівняння числових виразів.

    Мумзикам дуже сподобалась робота з числовою прямою і вони вирішили на ній поселитися. Кожний з них вибрав собі адресу:

Шапсик –5  · 2

Вопсик – 4  · 2 + 2

Таакава – 4  · 3 + 3

- Але як тільки мумзики з'явилися на числовій прямій, вони відразу посварилися...

-  Чому вони посварилися?  Як визначити?

-  Чи можна їх помирити?

IV. Закріплення вивченого матеріалу.

1. Робота в парах.

1. Визначте, які вирази живуть поміж даних.

2. Колективна робота.

Знайти на числовій прямій місце, де живуть такі числові вирази:

6  ·3             8  · 2 9  ·  2

                    5  · 3 + 1 6  · 3

  7  · 2 + 2 5  · 3+3

 7  · 2 + 4

3. Самостійна робота .

  Завдання на співвідношення числового виразу і величин.

V. Підсумок уроку.

- Що нового дізналися на уроці?

- Що можна помістити на числовій прямій?

 

 

 

 

 

 

 

Урок  7

 

Тема уроку. Самостійна робота.

Мета уроку. Перевірити рівень засвоєння вивченого матеріалу: вимірювання і побудова величин за допомогою додаткової мірки; запис результату вимірювання величин формулами, числовим виразом;

                          вміння визначати місце числового виразу на числовій

                      прямій. Розвивати пам'ять,логічне мислення.

                      Виховувати старанність, увагу, самостійність.

Обладнання уроку. Картки з індивідуальними завданнями.

 

Хід уроку

I. Організація класу.

II. Самостійна робота.

- Чим займалися на уроках математики?

- Чому з'явилася необхідність у використанні додаткової мірки?

- Як записати результат вимірювання?

- Про що розповідає кожне з чисел?

1. Виміряти величину А. Результат вимірювання записати числовим виразом.

 

 

     1          е_{1       .}

 

                е_{1       .}

 

                                  е_{1       .}

2. Задача.

   На уроці трудового навчання учні виготовляли гірлянду з різнокольорових прапорців. Коля, Ніна і Петро зробили по 5 прапорців, а Ганнуся ще 4.

1) Намалюй гірлянду, яку зробили діти. Прапорець познач так:

2) Скільки прапорців у гірлянді? Запиши відповідь у вигляді числового виразу.

3) Познач, де живуть на числовій прямій такі числові вирази:

4  · 2                4  · 2 + 1            5  · 3                   5  · 3 + 2

III. Підсумок уроку.

- Позначте, важко чи легко було виконувати завдання.

 

 Додаток 2

3 клас                                                            

Урок    математики

 

Тема уроку. Ділення з остачею.

Мета уроку. Закріпити вміння читати, записувати багатозначні числа,

                    виконувати з ними дії  (додавання, віднімання, множення).

                    Повторити табличне множення та  ділення.

                     Навчити виконувати ділення з остачею. Розвивати логічне

                     мислення, пам’ять, увагу. Виховувати вміння співпрацювати в парі,

                     виконувати завдання самостійно .

Хід урока:

І. Організація класу.

ІІ. Актуалізація знань учнів.

1.  Таблиця класів і розрядів.

• З чим ми працюємо на уроках математики?
• З якими числами?
• Придумайте свої багаторозрядні  числа. Запишіть.
• Давайте запишемо числа ... (5 чисел з різною кількістю знаків).
• Що ви можете зробити з цими числами? (Додати, відняти, помножити на 5)
• Виконайте дії. (Розв’язок прикладів на дошці та самостійно у зошитах.)

Взаємоперевірка. Колективна перевірка.

2.  Табличне ділення.

• А ділити такі числа ви вмієте? (Ні)
• А які ви вмієте поділити (Приклади дітей).
•  А звідки ви взяли ці приклади?
•  Отже, ви вмієте виконувати табличне ділення.
• Тоді, будь-ласка, розв’яжіть ці приклади:

          

         

3.  Перевірка завдання

• Перевіримо. Що трапилось з вами?
•  Чому ви не розв’язали останній приклад?
• Чому так багато різних відповідей?

ІІІ. Вивчення нового матеріалу

     1. Постановка навчальної задачі

      – Ми додаємо, віднімаємо будь-які числа? Чому ж ви не ділите будь-які числа?

• Що нам завжди допомагає розв’язати задачу? (Схема).
• Звернемося до схеми, щоб розв’язати цей приклад.

 

 

 

 

 

• Що це? (Числова пряма)
• Яке число треба відкласти на числовій прямій? (26).
•  Що треба з ним зробити? (Поділити на 4)
• Для полегшення роботи давайте візьмемо аркуш паперу такої ж довжини (Ось він).
•  Ви можете його розділити на 4 частини? Як? (Згорнути).
• Давайте подивимось де ж на схемі буде ця частина? (між 6 і 7).
• Отже ми поділили 26 на 4? (Так). А записати результат математично можемо? (Ні).
• Чому ми не можемо поділити число? (e_r не зручна) А яка зручна? (по 6, по 7)

 

 

 

 

 

 

 

 

 

 

 

• Де знаходиться наш результат? (Між числами 24 і 28)

Запишемо числові вирази до чисел 24, 28.

  

– А чи ви можете записати числовий вираз до нашого числа 26?

– З яким числовим виразом ми звикли працювати? (З першим.)

• У нашому числовому виразі що таке 2? (Остача).
• Ми поділили 26 на 4?

– Отже, як можна записати це: (ост. 2).

– Як назвали би ви цю дію? (Ділення з остачею).

IV.  Закріплення вивченого матеріалу.

1. Самостійна робота.

- Спробуйте розв’язати такі приклади:

а) (ост. 2)  – Як ви можете записати число 17 за допомогою числового виразу з 5?

б) ?

V. Підсумок уроку.

• Чому навчилися на уроці?

V. Домашнє завдання.

Скласти 4 приклади на ділення з остачею для сусіда, розв’язати самому.

4 клас                                                                                                            Додаток 3

  Урок  математики

 

Тема уроку. Додавання дробів з однаковими знаменниками.

Мета уроку. Вчити учнів додавати дроби з однаковими знаменниками.

Розвивати уміння складати за схемами задачі, розв'язувати задачі

різними способами. Розвивати логічне мислення, кмітливість.

Виховувати увагу, доброзичливі стосунки.

Обладнання уроку. Підручник, зошит, казкові герої, таблиці зі схемами до

                     задач.

Хід уроку

I.             Організація класу.

II.            Повторення вивченого матеріалу.

1.   Бесіда.

- Що вміємо робити з дробами?

2.   Усний рахунок.

а) Утворіть і прочитай всі можливі дроби, якщо:

Чисельник                              Знаменник

     2; 3; 1.                                       8; 4; 7.

б) Порівняти дроби з однаковими знаменниками:

.  (Висновок про порівняння дробів з однаковими знаменниками).

в) Порівняти дроби з однаковими чисельниками:

.  (Висновок  про  порівняння  дробів  з  однаковими чисельниками).

г) Серед поданих дробів назвати правильні дроби?  неправильні дроби? мішані числа?

3. Знайти місце дробів на числовій прямій:  

4.  Плямс приготував для вас завдання. Визначте, до якої схеми належить кожний вираз?

 

 

 

 

 

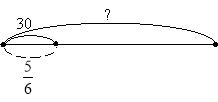
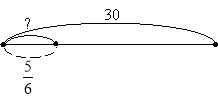
а)

б)

• Складіть усно задачі до кожної схеми.
• Як знайти дріб від числа та число за його дробом?

III. Вивчення нового матеріалу.

1.   Постановка навчальної задачі.

Буратіно побачив у підручнику числовий вираз і замислився.

?

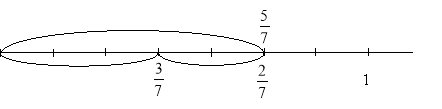- Попрацюйте в парі та спробуйте допомогти Буратіно впоратися з цим завданням. - Користуйтеся числовою прямою.

 

 

 

 

    0

- Який висновок можна зробити про додавання двох дробів з однаковими знаменниками?

2.  Фізкультхвилинка.

3.  Самостійна робота учнів.

-   Виконайте додавання дробів без числової прямої.

 1-в.                                         2-в.

                                  

                            

4. Робота над задачею.

    Мальвіна до приходу гостей напекла пиріжків. З усього тіста в неї вийшло 36

пиріжків.    усіх пиріжків були з картоплею, – з капустою, а решта – з

вишнями. Скільки пиріжків з вишнями напекла Мальвіна?

а) Накресліть схему до задачі.

б)Подивіться, які схеми до цієї задачі накреслили друзі:

 

 

 

 

 

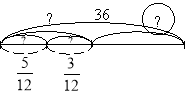
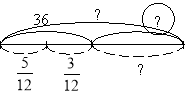
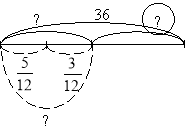
Буратіно                                  П'єро                                Мальвіна

-   Хто з друзів впорався із завданням?

-   Хто припустився помилок? Чому?

в) Розв'яжіть задачу.

1-спосіб

1)   (п.) - з картоплею.

2)   (п.)  - з капустою.

3)    (п.) - з картоплею та капустою.

4) (п.)

 

2-спосіб

1) частин становлять пиріжки картоплею та капустою.

2) (п.) – становлять пиріжки з картоплею та капустою.

3)   (п.)

-   Який із способів розв'язання задачі  більш раціональний?

-   Чому?

IV.     Підсумок уроку.

-   Як додавати дроби з однаковими знаменниками?

V. Домашнє завдання.

с. 67(вивчити правило),

№ 144,  № 151 (високий рівень – розвязати задачу різними способами).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаної літератури

 

1.    Давидов В.В. Теорія розвивального навчання. – Москва: ІНТОР,

       1996. – 544с.

2. Репкін В.В., Репкіна Н.В. Розвивальне навчання: теорія і практика. Статті -    Томськ:”Пеленг”, 1997. – 288с.
3. Енциклопедія педагогічних технологій та інновацій /Автор-укладач Н.П. Наволокова. – Х.: Вид. група “Основа”, 2009. – 176.
4. Цукерман Г.А. Навіщо дітям навчатися разом? – М.: Знання, 1985. – 80с.
5. Захарова Г.М. Математика, 1 клас. Підручник-зошит. – Х.: ННМЦ “Розвивальне навчання”, 2007.
6. Захарова Г.М. Математика, 2 клас. Підручник-зошит. – Х.: ННМЦ “Розвивальне навчання”, 2003.
7. Захарова Г.М. Математика, 3 клас. Підручник-зошит. – Х.: ННМЦ “Розвивальне навчання”, 2008.
8. Захарова Г.М. Математика, 4 клас. Підручник-зошит. – Х.: ННМЦ “Розвивальне навчання”, 2009.
9. Програми для початкових класів загальноосвітніх шкіл. Система розвивального навчання Д.Б. Ельконіна – В.В. Давидова. - Х.: ННМЦ “Розвивальне навчання”, 2003.
10. Захарова Г.М., Мельник К.І., Жемчужкіна Г.В. Методичний посібник для вчителя. Математика 1 клас. - Х.: ННМЦ “Розвивальне навчання”, 2009. – 96с.