МІНІСТЕРСТВО ОСВІТИ І ІНАУКИ УКРАЇНИ

КОЛЕДЖ ПРОМИСЛОВОЇ АВТОМАТИКИ ТА ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

ОДЕСЬКОЇ НАЦІОНАЛЬНОЇ АКАДЕМІЇ ХАРЧОВИХ ТЕХНОЛОГІЙ

Тестові завдання

з теорії ймовірностей та математичної статистики

Методичні вказівки для самостійної роботи студентів спеціальностей:

5.05010301 «Розробка програмного забезпечення»

122 «Комп’ютерні науки та інформаційні технологій»

Одеса – 2019 р.

Оксаніченко В.Л. Тестові завдання з теорії ймовірностей та математичної статистики:  Методичні вказівки для самостійної роботи студентів. Коледж промислової автоматики та інформаційних технологій Одеської національної академії харчових технологій, 2019 р. – 25 с.

Вказівки складені відповідно навчальної програми, містять тестові завдання з дисципліни «Теорія ймовірностей та математична статистика». Докладно розглядаються методи розв’язання тестових завдань різного ступеня складності із зазначенням необхідного теоретичного матеріалу.

Методичні вказівки містять приклади, розв’язання яких дозволить студентам самостійно оволодіти відповідними навичками розрахунку ймовірності появи подій та характеристик випадкових величин.

Рецензент: Флешеровська О.В., голова обласної методичної комісії викладачів математики, викладач вищої кваліфікаційної категорії, викладачметодист.

Розглянуто та рекомендовано до видання на засіданні циклової комісії математичних та природничих дисциплін.

Протокол № 5 від «28» березня 2019 р.

ЗМІСТ

Вступ…………………………………………………………………………… 4 1. Алгебра подій........................................................................................................... 5

2. Обчислення ймовірностей подій......................................................................... 6

3. Випадкові величини та їх розподіли................................................................ 12

4. Вибіркові випадкові величини та їх оцінки..................................................... 17

5. Тестові завдання для самоперевірки................................................................ 21

ВСТУП

Основою даних методичних вказівок є зміст лекцій з дисципліни «Теорія ймовірностей та математична статистика» для студентів спеціальностей 5.05010301 «Розробка програмного забезпечення», 122 «Комп’ютерні науки та інформаційні технології».

Методичні вказівки повинні допомогти студентам оволодіти основами теорії ймовірностей. Наведено велику кількість обов’язкових вправ, які повинні служити елементом контролю (самоконтролю) над засвоєнням матеріалу.

На лекційних та практичних заняттях студенти повинні ознайомитися з основними імовірнісними закономірностями, статистичними ідеями та підходами, а також набути базові навички розв’язання задач. Тестові завдання, наведені у методичних вказівках, в простій та доступній формі, дозволять студентам закріпити пройдений матеріал. Крім того, детально розглянуті завдання можуть стати основою при підготовці до практичних занять, а також при виконанні домашнього завдання.

1.   Алгебра подій

1.1. Що означає операція A B?

а) після події а відбудеться подія В;

б) відбулася хоча б одна з подій А або В;

в) одночасно відбулись події А та В.

За означенням, результатом операції суми двох подій _C  _A _B є подія, яка полягає в тому, що відбувається принаймні одна з подій А або В. Правильна відповідь: (б).

1.2. Оберіть неправильне твердження:

а) подія, протилежна вірогідній, є неможливою;

б) сума ймовірностей двох протилежних подій дорівнює одиниці;

в) якщо дві події єдино можливі та несумісні,, то вони називаються

протилежними;

г) ймовірність появи однієї з протилежних подій завжди більше

ймовірності іншої.

Розглянемо кожен варіант відповіді. Варіант (а) правильний – подія, протилежна неможливій події, є вірогідною. Знайдемо ймовірність p(A  A)  p()  1; отже, за третій аксіомі аксіоматичного визначення ймовірності – ймовірність суми двох несумісних подій дорівнює сумі їх ймовірностей, маємо: _p(A)  _p(A)  ₁, (б) правильне. Подія називається неможливою, якщо вона не може відбутися в умовах даного випробування. Протилежна подія _A відбувається тоді й тільки тоді, коли не відбувається подія А, причому _A _A  , (в) правильне. Ймовірність настання будь-якої події лежить у інтервалі [0;1]. З цього не випливає правильність (г). Неправильне твердження: (г).

1.3. Випробування складається з підкиданні один раз грального кубика. Подія А={випало число очок більше трьох}; Подія В={випало парне число очок}. Тоді множина, що відповідаю події А+В, є:

а) A B  6;

б) A B  4, 6;

в) A B  2, 4, 5, 6;

г) A B  3, 4, 5, 6

Множина, що відповідає сумі двох подій _{A B}, є об’єднання множин

A _B. Множина А включає елементарні результати A B  4, 5, 6, множина

B  2, 4, 6. Об’єднання множин A B  4, 5, 6; 2, 4, 6 2, 4, 5, 6. Правильна відповідь: (в).

1.4. Випробування складається з підкиданні один раз грального кубика.

При яких подіях А,В правильне: А тягне за собою В?

а) А={випало непарне число очок}, В={випало число 3};

б) А={випало число 2}, В={випало парне число очок};

в) А={випало число 6}, В={випало число очок, менше 6}.

Операції над подіями «А тягне за собою В» в термінах теорії множин відповідає операція включення множин. Для кожного варіанта відповіді визначимо множини А,В.

(а) A  1, 3, 5, B  3 умова A  _B не виконана;

(б) A  2, B  2, 4, 6 умова A  _B виконана;

(в) A  6, B  1, 2, 3, 4, 5 умова A  _B не виконана. Правильна відповідь: (б).

1.5. Навмання обрана деталь може виявитися або першого (подія А), або другого (подія В), або третього (подія С) сорту. Що уявляє собою подія:

A C ?

а) {деталь першого або третього сорту};

б) {деталь другого сорту};

в) {деталь першого та третього сорту}.

Спочатку виконаємо операцію суми подій. Результат А+С={деталь першого або третього сорту}. Тепер запишемо протилежну подію

A _C = {деталь не першого, не третього сорту}={деталь другого сорту}.

Правильна відповідь: (б).

2.   Обчислення ймовірностей подій

2.1. Гральний кубик підкидають один раз. Ймовірність того, що на верхній грані випаде число очок більше трьох, дорівнює:

а) 1 ;

3

б) 1 ;

2

в) 2 .

3

             Визначимо     множину     усіх     можливих     результатів     випробування

  w₁,w₂,w₃,w₄,w₅,w₆, w_k  X  k, k 1, 6. Кількість результатів N()  6. Події А={випаде число очок, більше трьох} відповідає множина, що включає результати A  w₄,w₅,w₆, N(A)  3. Згідно класичного означення ймовірності, ймовірність події А - це відношення числа _N(A), що сприяє появі даної події до загальної кількості _N(₎ усіх можливих результатів даного випробування

                    N(A)      3     1

p(A)    .

N() 6 2

Правильна відповідь: (б).

2.2. В урні 5 білих, 3 чорних, 4 червоних куль. Ймовірність того, що з урни виберуть білу або чорну кулю дорівнює:

а) 1 ;

4

б) 15 ;

8

в) 2. 3

Всього в урні лежить (5+3+4) куль. Загальна кількість можливих результатів даного випробування _N(₎ ₁₂ . Результатів, що сприяють появі

події      А      =      {вибрали      кулю      білого      або      чорного      кольору}

N_(A)=5(білих)+3(чорних)= 8 куль. Ймовірність події А, згідно класичного

означення ймовірності, дорівнює _{p(A) } ^N(A) _ ⁸ _ ² .

                                                                                                                      N()      12     3

Правильна відповідь: (в).

2.3. В групі 7 юнаків та 5 дівчат. На конференцію обирають трьох студентів випадкова чином (без повернення). Визначте ймовірність того, що на конференцію оберуть двох юнаків і одну дівчину.

             а) 11      ;

28

              б) 21     ;

44

              в) 21        .

110

Представимо множину студентів групи у вигляді занумерованої множини {1,2,3,4,5,6,7; 8,9,10,11,12}, де перші 7 елементів множини – юнаки, останні 5 – дівчата.

Вибір студентів на конференцію здійснюється випадковим чином без повернення та без упорядкування. Кількість таких можливих варіантів вибору трьох студентів з групи (12 людей) визначається за допомогою

формули числа комбінацій N()  C123  12!  12!  9!101112  220. 3!(12  3)! 3!9! 1 239!

Розглянемо подію А = {вибрали двох юнаків та одну дівчину}, тобто з множини елементів {1,2,3,4,5,6,7} вибираємо 2 елемента, таких способів

C₇²                                    21; з множини {8,9,10,11,12} вибираємо один

!

елемент C51       5!         5!  5 способів.

                                     1!(5 1)!  1!4!

Необхідно одночасно вибрати трьох студентів (відповідно до події А), тому число результатів, що сприяють даній події А, дорівнює

N(A)  C₂² C₅¹  215 105. Згідно з класичним означенням ймовірності,

                    N(A)      105      21

p(A)                        .

                    N()      220     44

Правильна відповідь: (б).

2.4. В урні 6 білих та 4 чорних кулі. З урни дістають дві кулі. Ймовірність того, що обидві кулі чорного кольору, дорівнює:

а) 2;

5

              б) 2     ;

15

в) 1 . 4

Всього в урні N()  6  4 10 куль. Введемо дві події: А = {перша вийнята куля чорна}, В = {друга вийнята куля чорна}. Необхідно обчислити ймовірність одночасної появи двох подій А та В, тобто _p(AB).

Події А та В залежні: якщо відбувається подія А (змінюється загальна кількість куль в урні і кількість куль чорного кольору, що залишились), то ймовірність події В зміниться. Тому за теоремою добутку ймовірностей p(AB)  p(A) p_A (B) . Ймовірність події А, згідно з класичним означенням

ймовірності, p(A)  4  2 .

                                                         10     5

Якщо подія А відбулась, кількість куль в урні зменшилась на одну:      (10-1)=9. Кількість результатів, що сприяють також зменшилась – в урні залишилось (4-1)=3 чорні кулі. Умовна ймовірність _pA (_{B) } ³ _ ¹ . Шукана

                                                                                                                                                                                       9     3

ймовірність p(A)  2  1  2 .

                                                        5 3      15

Правильна відповідь: (б).

2.5. Два стрільця роблять по одному пострілу. Ймовірність влучення в ціль для першого та другого стрільців дорівнює 0,6 та 0,9 відповідно. Тоді ймовірність того, що ціль буде вражена, дорівнює: а) 0,54;

б) 0,96;

в) 0,996.

Перший спосіб. Розглянемо подію А = {перший стрілок влучив у ціль}, В = {другий стрілок влучив у ціль}. Ймовірності влучення відповідно першого та другого стрільців p(A)  0,6, p(B)  0,9, ймовірності промаху для першого та другого стрільця відповідно p(A)  1 p(A)  1 0,6  0,4; p(B)  0,1. Необхідно знайти ймовірність того, що відбудеться подія С = {ціль буде вражено}={хоча б один з стрільців влучить у ціль}, тобто можливі такі події:

C₁ = {влучить перший і не влучить другий}, _C2 = {не влучить перший і  влучить другий}, _C3 = {обидва стрільця влучать}. В алгебрі подій А,В подія

С, що нас цікавить записується у вигляді: C  C₁  C₂  C₃  AB  AB  AB.

Знайдемо ймовірність події С: p(C)  p(AB  AB  AB) =[події AB, AB, AB попарно несумісні, якщо відбуваються А та В, то не можуть відбутися A_{B, AB}, отже ймовірність суми попарно несумісних подій дорівнює сумі їх ймовірностей] = p(AB)  p(AB)  p(AB)= [події А та В незалежні, оскільки стільці роблять постріли незалежно один від одного: влучення або промах одного стрільця відбувається незалежно від іншого стільця]

 p(A)  p(B)  p(A)  p(B)  p(A)  p(B)  0,60,1 0,40,9  0,60,9  0,96

Другий спосіб. Простіше при визначенні ймовірності події С = {хоча б один з стрільців влучить у ціль} розглянути протилежну подію _C = {перший та другий стільці не влучать у мішень}: _C  _A  _B та обчислити її ймовірність.

За теоремою добутку ймовірностей для незалежних подій p(C )  p(A  B)  P(A)  P(B)  0,40,1  0,04 . Ймовірність протилежної події

p(C) 1 0,04  0,96.

Правильна відповідь: (б).

2.6. Кількість перестановок у слові «ТВМС» дорівнює: а) 4;

б) 16;

в) 24.

Таких перестановок буде _4! ₂₄. Перша буква «Т» може бути переставлена на будь-яке з чотирьох місць: друга буква «В» - на будь-яке з трьох місць, що залишились; «М» - на будь-яке з двох місць; буква «С» може зайняти лише одне останнє місце, тобто ₁₂₃₄  ₂₄. Правильна відповідь: (в).

2.7. Скільки різних двозначних чисел можна скласти з п’яти цифр 1,2,3,4,5, якщо всі цифри у числі різні?

а) 25;

б) 60;

в) 20.

Перший спосіб. Множина всіх можливих двозначних чисел, що складаються з цифр 1,2,3,4,5, запишемо у вигляді  _ (a,b) a  1,5, b  1,5.

Таких чисел N()  55  25. Розглянемо подію А = {цифри у числі різні}. З множини _ вибираємо результати, що сприяють появі події А:

A _ (a,b) a  1,5, b  1,5,a  b, тобто з множини виключаємо варіанти (1,1),

(2,2), (3,3), (4,4), (5,5). Таким чином, N(A)  255  20.

Другий спосіб. Розглянемо інший варіант підрахунку кількості елементів множини А. перша цифра може бути будь-якою: 1,2,3,4,5 (5 варіантів); друга цифра може бути будь-якою від 1 до 5, крім цифри, яка вже записана першою (5-1=4 варіанта). Число складається одночасно з двох цифр, тобто таких двозначних чисел N(A)  54  20 . Правильна відповідь: (в).

2.8. Гральний кубик підкидають 5 разів. Ймовірність того, що 3 рази з’явиться непарна грань, дорівнює:

              а) 1      ;

32

              б) 1     ;

16

              в) 5      .

16

У даному випробування {підкидання грального кубика 5 разів} подія, що нас цікавить А = {випала непарна грань} з’явиться 3 рази, отже, протилежна подія _A = {випала парна грань} з’явиться 2 рази. Умову випробування можна рахувати як поява успіху {непарна грань} або невдачі {парна грань} в серії _n випробувань.

Ймовірність появи успіху при одному підкиданні _p1  _{p(A) } ³ _ ¹ ,

                                                                                                                                                                                                                 6        2

ймовірність невдачі при одному підкиданні                   _p2  _{p(A) } ³ _ ¹ . Загальна

                                                                                                                                                                                   6     2

кількість випробувань n  ₅, в яких спостерігається m  ₃ успіхів та((n  m)  2 невдач. Ймовірність появи _{m  3} успіхів визначається за формулою

                                                                                                                                                                               3             2

біноміальних ймовірностей: P_n5(m  3)  C_n^m  p₁^m  p₂^nm  C₅³ ^{ 1 } ^{ 1 }   

                                                                                                                                                                     2   2

5

        5!    1     10      5

                    .

3!2!  2      32     16

Правильна відповідь: (в).

2.9. До магазину надійшло 30% телевізорів фірми L, інші – фірми N. В продукції фірми L брак складає 20% телевізорів; фірми N – 15%. Ймовірність навмання вибрати телевізор без браку складає: а) 0,835;

б) 0,65;

в) 0,105.

Визначимо подію, що нас цікавить, як А = {навмання вибрали телевізор без браку}. Телевізори поступили з двох фірм. Приймемо у якості гіпотез події _H1 = {телевізор фірми L}, _H2 = {телевізор фірми N}. Подія А відбудеться лише при сумісному відбуванні з однією з гіпотез _H1 або _H2.

Події _H1, _H2 утворюють повну групу подій, жодних інших припущень немає.

Необхідно обчислили ймовірність події А = {навмання вибрали телевізор без браку}. Для обчислення застосовують формулу повної ймовірності p(A)  p(H₁) p_H1 (A)  p(H₂ ) p_H2 (A). Товару фірми L надійшло 30%, тобто

ймовірність обрання телевізора фірми L складає _{p(H 1}) _ ^30%  _0,3; з фірми N

100%

надійшло (100-30)%, тобто p(H ₂)  0,7 .

Ймовірність браку відома, обчислимо відсоток надійних телевізорів фірми L (100-20)%=80%, фірми N – (100-15)=85%.

Ймовірність вибрати телевізор без браку, якщо він фірми L, є умовна ймовірність p_H1 (A)  0,8; фірми N - p_H2 (A)  0,85. Обчислимо ймовірність p(A)  0,30,8 0,70,85  0,24  0,595  0,835. Правильна відповідь: (а).

2.10. Яке найімовірніше число стандартних деталей серед 15 перевірених відділом технічного контролю, якщо ймовірність того, що деталь стандартна, дорівнюю 0,7?

а) 9;

б) 10;

в) 11.

Число _k0 (настання події в незалежних випробуваннях, в кожному з яких ймовірність появи події А дорівнює _p ) називають найімовірнішим, якщо ймовірність того, що подія відбудеться в цих випробуваннях _k0 разів, перевищує (або, принаймні не менше) ймовірності інших можливих результатів випробування.

Найімовірніше число _k0 визначають з подвійної нерівності np  q  k₀  np  p , причому

(1) – якщо _np  _q дробове, то існує одне найімовірніше число _k0 ; (2) – якщо np  _q ціле, то існує два найімовірніших числа k₀ та k₀ 1;

(3) – якщо _np ціле, то найімовірніше число k₀  np.

Ймовірність появи події А = {навмання вибрали стандартну деталь} p(A)  p  0,7; ймовірність протилежної події q 1 p  0,3. Кількість деталей,

що перевіряють – це число випробувань - n 15. Визначимо np 150.7 10,5 дробове. Обчислимо np  q 150,7  0,3 10,5 0,3 10,2 - дробове, отже, застосовуємо правило (1). Верхня границя інтервалу np  p 150,7 11,2 .

Найімовірніше число визначимо з інтервалу 10,2  k₀  11,2  k₀  11. Правильна відповідь: (в).

2.11. Чому дорівнює ймовірність відмови пристою, який складається з трьох незалежно працюючих елементів з відповідними ймовірностями відмови елементів 0,1; 0,2; 0,05, якщо для цього достатньо, щоб відмовив хоча б один елемент?

а) 0,316;

б) 0,35;

в) 0,001.

Роботу пристрою зручно представити у вигляді схеми. З’єднання елементів послідовне: якщо відмовить хоча б один елемент, то схема не працює (мал. 1)

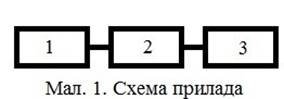
Знайдемо ймовірність події В= {прилад відмовить}. Розглянемо події A₁= {перший елемент відмовить}; A₂ = {другий елемент відмовить};

A₃ = {третій елемент відмовить} та відповідні протилежні події _Ak = {елемент з номером _k працює}, _k _1,2,3. Відомі ймовірності відмови кожного елемента

p(A₁)  0,1; p(A₂)  0,2;                 p(A₃)  0,05 . Надійності елементів p(A₁)  1 0,1  0,9;

p(A₂ )  1 0,2  0,8 ; p(A₃) 1 0,05  0,95.

Можуть вийти з ладу лише перший елемент, лише другий елемент, перший та третій, і т.д. простіше розглянути протилежну подію _B = {прилад працює}.

Запишемо _B в алгебрі подій _A1, _A2._A3 . Прилад працює, якщо усі три елементи працюють: B  A₁  A₂  A₃ .

Ймовірність події дорівнює p(B)  p(A₁  A₂  A₃) = [оскільки елементи працюють незалежно, то за теоремою добутку ймовірностей отримаємо]=

 p(A₁) p(A₂ ) p(A₃)  0,90,80,95  0,684.                Шукана                 ймовірність

p(B)  1 p(B)  1 0,684  0,316 . Правильна відповідь: (а).

2.12. Скільки існує тризначних чисел, у записі яких немає чисел 5 та 6? а) 296

б) 448;

в) 1024.

             Множину     можливих     тризначних     чисел     запишемо     у     вигляді

 _ (a,b,c) a  1,9, b  0,9, c  0,9. Всього тризначних чисел N()  91010  900 .

Розглянемо подію А= {в записі числа немає цифр 5 та 6}. З множини 

виберемо          результати,          що         сприяють         даній         події         А:

A _ (a,b,c) a  1,2,3,4,,7,8,9; b  0,1,2,3,4,,7,8,9;c  0,1,2,3,4,7,8,9.          Кількість           таких результатів визначається N(A)  788  448.

Правильна відповідь: (б).

3.   Випадкові величини та їх розподіли

3.1. Заданий закон розподілення дискретної випадкової величини Х

Чому дорівнює значення ймовірності _p5 ?

а) 0,1

б) 0;

в) 0,09

Законом розподілу випадкової величини Х дискретного типу називається перелік всіх можливих значень випадкової величини та відповідні цим значенням ймовірності. Події _X  _x1, _X  _x2 утворюють повну групу подій, тобто . Сума ймовірностей PX  x₁ PX  x₂... 1. Необхідно обчислити

5

невідоме значення p₅ ^{з рівняння}  p_i 1; p₅  1 (0,14  0,28  0,17  0,32)  0,09 .

i1

Правильна відповідь: (в).

3.2. Нехай Х – випадкова величина з функцію розподілу:

                              0,         x  0



                             0,2,   0  x  2

         F(X ) ^{ }0,4,   2  x  4



                            0,9,   4  x  6



                              1,         x  6

Чому дорівнює мода випадкової величини Х?

а) 2

б) 4;

в) 6.

Випадкова величина Х – дискретного типу. Мода випадкової величини Х дискретного типу визначається як таке можливе значення _xm , для якого PX  x_m  max PX  x_k . Мода є найбільш ймовірним значенням випадкової

k величини Х у випадку, якщо таке значення єдине. Для визначення моди випадкової величини Х опишемо закон розподілення у вигляді таблиці 1.

F(x)  PX  x PX  x_i , де i : x_i  x .

F(0)  0  PX  0.

F(2)  0,2  PX  2 PX  0.

F(4)  0,4  PX  4 PX  0 PX  2 PX  2 0,4  0,2  0,2

F(6)  0,9  PX  6 PX  0 PX  2 PX  4 0,2  0,2  PX  4

 PX  4 0,9  0,4  0,5

F(8) 1 PX  8 PX  0 PX  2 PX  4 PX  6 0,2  0,2  0,5

 PX  6 PX  61 0,9  0,1

Таблиця 1. Закон розподілення випадкової величини Х

Мода випадкової величини Х дорівнює _x3  ₄ , оскільки найбільша ймовірність PX  4 0,5.

Правильна відповідь: (б).

3.3. Закон розподілення випадкової величини Х задано у вигляді таблиці

Чому дорівнює математичне очікування випадкової величини Х? а) 2,9;

б) 3,5;

в) 4.

Математичним очікування випадкової величини Х дискретного типу називається дійсне число, яке визначається за формулою

M[X ]  x_k  PX  x_k . M[X] 10,1 20,4  30,2  40,1 50,2  2,9.

k

Правильна відповідь: (а).

3.4. Випадкову величину Х задано за допомогою таблиці

Чому дорівнює математичне очікування величини _M[X ² _1] ? а) 11,1;

б) 21;

в) 22,1.

Запишемо закон розподілу для нової випадкової величини _Y  _X ² ₁:

Обчислимо       математичне       очікування       випадкової       величини       Y:

M[Y] | M[X ² 1]  50,1100,5 17  0,3  11,1. Правильна відповідь: (а).

3.5. Закон розподілення випадкової величини Х задано у вигляді таблиці

Чому дорівнює дисперсія випадкової величини Х? а) 2,8;

б) 1,96;

в) 1,51.

Дисперсією випадкової величини Х називається невід’ємне число

D[X]  D_X ,                  яке                 обчислюється                 за                формулою

D_X  M[(X  M[X ])² ]  M[X ]  (M[X ])² .

Для дискретної випадкової величини Х диспепсія обчислюється за формулою D_X  x_k  m_X ²  p_k  x_k ²  p_k  m_X ².

                                                  k                                               k

Обчислимо спочатку математичне очікування випадкової величини Х :

M[X] 10,3 30,5 50,2  2,8. Дисперсія

D_X  (1²  0,3  3² 0,5  5² 0,2)  (2,8)²  10,3 90,5 250,2)  7,84  9,8 7,84 1,96. Правильна відповідь: (б).

3.6. При проведенні контролю якості серед 100 навмання обраних деталей 2 виявились бракованими. Серед 5000 деталей бракованими

виявляться:

а) 250;

б) 100;

в) 50.

В даному випробування множина всіх результатів включає два елементи  {w₁,w_2}, де w₁ = {деталь бракована}, w₂ = {деталь стандартна}.

Ймовірності результатів відповідно дорівнюють p(w₁)  p₁  2 0,02 ;

100

p(w₂)  p₂ 1 p₁  0,98. Таким чином, випадкова величина Х має біноміальний розподіл. Шукана кількість бракованих деталей є найбільш ймовірним значенням випадкової величини Х – математичне очікування, яке визначається для такої випадкової величини за формулою

M[X]  n p  0,025000 100 деталей.

Правильна відповідь: (б).

3.7. Випадкова величина Х рівномірно розподілена на відрізку [-7; 18].

Чому дорівнює ймовірність P(3  X)?

             а) 15      ;

25

              б) 21     ;

25

в) 11     . 15

Випадкова величина називається рівномірно розподіленою, якщо її

                                                                                                                            1

щільність розподілу ймовірності _{f (x) } ^_{b  a} ^{,      x[a,b]}. Довжина відрізка     

                                                                                                                          0,         x[a,b]

[-7;     18]     складає     b  a 18 (7)  25.     Запишемо     функцію     щільності

 1 f (x)  ^25 ^{,          x[7,18]}. Ймовірність влучення випадкової величини Х в  0,     x[7,18]

b

заданий      інтервал     визначається      за     формулою     p(a  X  b)   f (x)dx.

a 

Ймовірність               p(3  X  )   f (x)dx . Функція щільності ненульова на

3

відрізку [-7; 18], тому інтеграл p(3  X  )  ¹⁸^3 f (x)dx  ^18 f (x)dx  ¹⁸^3₂₅¹ dx 

14243

0

         x ¹⁸        21

               .

      25 _3       25

Правильна відповідь: (б).

3.8. Чому дорівнює значення невідомого параметра а функції щільності

                                   0,           x[4,6]



           f (x)  a  x  1,  x[4,6]?

                                     8

а) 1 ;

2

б) 1 ;

4

в) 1 .

8

Параметр а можна знайти з умови нормування (властивість функції



щільності  f _(x)dx ₁. Функція щільності _{f (x)} ненульова на відрізку [4; 6] та

 перетворюється на нуль поза даного інтервалу. Тому інтеграл можна розбити на три частини:

                         4               6          1                     6          1       a x2     x  6      a36    6

f (x)dx  0dx  4 a x  8dx  6 0dx  4 a x  8dx           2                                                                                                    8  4   2      8 

 a 16     4            1                    1

           10a  1 a  .

     2       8             4                    8

Правильна відповідь: (в).

3.9. Нехай Х – випадкова величина з функцією розподілу:

                                                                                                      0,            x  1

                                                                                                      x

                                                                              F(x)  _x ₆ ,1  1  x  2

  , 2  x  3 8 2

                                                                                                   1,            x  3

Чому дорівнює ймовірність _PX  1 ?

2

             а) 11     ;

12

              б) 1     ;

12

в) 5 . 6

За визначенням, функція розподілу випадкової величини Х є ймовірність

F(x)  PX  x. Тому розглянемо протилежну події           A _ X  ¹  подію

2

A   _\ A   _\ X  1 _ X  1 . Ймовірність суми   протилежних     подій

                                                       2                  2

дорівнює            одиниці:           P(A)  P(A)  1.          Шукана           ймовірність

PX _ ₁ _PX  1  ₁ _F1 . На інтервалі [1; 2) функція розподілу

                                                           2                  2

F_(x)  _{x 6} ,         тому          _F(1 _{) } ¹ _ ¹ _ ¹ .         Тоді        шукана        ймовірність

² 6 2 12

PX 1  . 1 11 12 12

Правильна відповідь: (а).

3.10. Неперервна випадкова величина Х задана щільністю розподілу

2 (X 5) ймовірності _{f (X) } ^ . Чому дорівнює дисперсія ці їх нормально

розподіленої величини?

а) 4

б) 16;

в) 5.

Щільність ймовірності нормально розподіленої випадкової величини Х з математичним очікуванням m_X та дисперсією D_X   _X² має вид

(X mX )2

f _{(X )}  , де  _X - середнє квадратичне відхилення випадкової

X величини Х. Стандартне відхилення  _X  ₄; дисперсія випадкової величини Х D_X   _X²  4²  16 .

Правильна відповідь: (б).

3.11. Щільність ймовірності випадкової величини Х, що розподілена за експоненціальним законом з параметром _{  2} має вид:

      а) _{f (x) } _ 02,x     x  0 ;

                                 e     ,    x  0

       б) _{f (x) } _ 0,2x      x  0 ;

                                  2e     ,    x  0

                                    0,        x  0

      в) f (x)  1 e2x ,   x  0.

2

Випадкова величина Х називається розподіленою за показниковим (експоненціальним) законом з параметром _{  0}, якщо вона неперервного типу та її щільність розподілу ймовірності задається за формулою

                     0,        x  0

f (x)      _x                     . Параметр   2.

                 e     ,    x  0

Правильна відповідь: (б).

4.   Вибіркові випадкові величини та їх оцінки

4.1. По виборці _n  ₂₀₀ побудована гістограма частот

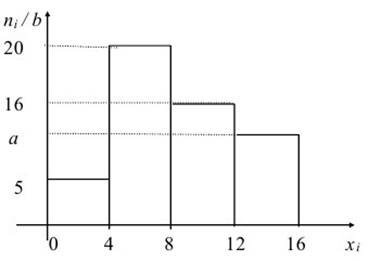
Чому дорівнює значення а?

а) 9;

б) 10;

в) 11.

Гістограмою частот групованої вибірки називається кусково-постійна функція, яка побудована на інтервалах групування і приймає на кожному з них значення ⁿⁱ , _i _1,2,...,k відповідно. Площа ступінчастої фігури під b

графіком гістограми дорівнює об’єму вибірки _n. Сума ⁿⁱ дорівнює об’єму

b

вибірки, поділеному на довжину інтервалу групування. За малюнком видно, що довжина інтегралу b  4  0  4.

Просумуємо 20 16  a  5    41 a  50  a  9 .

Правильна відповідь: (а).

4.2. Чому дорівнює оцінка математичного очікування вибіркової випадкової величини 1, 3, 1, 2, 2, 4, 1?

а) 3;

б) 2,3;

в) 2.

Математичне очікування вибіркової випадкової величини або вибіркове середнє визначається за формулою _m^*_X  _{x } ¹n _jⁿ1 _{x j} , де _n - об’єм вибірки. n  7, M _X  (1 31 2  2  4 1)/7  2.

Правильна відповідь: (в).

4.3. Для     якої вибірки,    представленої   у        вигляді     групованого статистичного ряду, побудовано полігон частот?

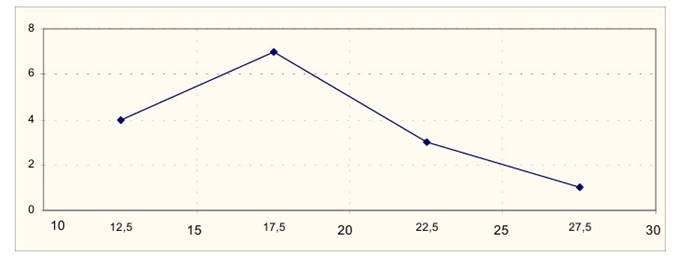
а)

б)

в) немає правильної відповіді.

Полігоном частот називається ламана з вершинами у точках ^_zi , ^{ni }_,

                                                                                                                                                                                                                  b 

i _1,2,...,k ; _zi - середина відповідного інтервалу, ⁿⁱ - частота, що поділена на b

довжину інтервалу. Довжина інтервалу _b _17,5 _12,5  ₅. Середини інтервалів z_i : 12,5; 17,5; 22,5; 27,5. Варіант (б) не підходить. Визначимо частоти: для першого інтервалу (10;15) ⁿ¹ _ ⁿ¹ _{ 4} , звідки b       5

n₁  45  20;     для     другого     інтервалу     (15;20)        ⁿ² _ ⁿ²  7  n₁  75  35;

                                                                                                                                                            b        5

n₃  35  15; n₄ 15  5. Варіант (а) не підходить. Правильна відповідь: (в).

4.4. Як записується емпірична функція розподілу для вибіркової випадкової величини, яка задана статистичним рядом?

 0,



а) F(x)  _0,2, _0,7,

 1,

x  2,

2  x  3, 3  x  6, x  6

 0,        x  2,



            б) F(x)  0,2,   2  x  3,;

                                      _0,5,   3  x  6,

                                     1,        x  6

                                            0,               x  2,



           в) _{F(x) } _0,2  0,5x,   2  x  3,_.

                                     _0,5  0,3x,   3  x  6,

                                        1,               x  6

Емпіричною функцією розподілення називають функцію _F ^*_(x) , що визначає для кожного значення х відносну частоту події _X  _x : _F ^*_{(x) } ^nx , де n n_x - число варіант, менших х; _n - об’єм вибірки.

Емпірична функція володіє наступними властивостями:

•        Значення _F ^*_(x) належать відрізку [0; 1];

•        F ^*(x) - неспадна функція;

•        Якщо x₁ - найменша варіанта; а x_k - найбільша, то F ^*(x)  0 при x  x₁ та

F ^*(x)  1 при x  x_k .

3

                  Знайдемо об’єм вибірки       n  n_i  2  5 3 10 .      Найменша варіанта

i1

дорівнює двом, тому F ^*(x)  0 при x  2. Значення X  3, а саме x₁  2 , спостерігалось двічі, отже, F ^*(x)    0,2 при 2  x  3. Значення X  6, а саме x₁  2 та x₂  3, спостерігались 2  5  7 разів, отже, F ^*(x)    0,7 при

4   x  6.  Оскільки x₃  6 - найбільша варіанта, то F ^*(x)  1 при x  6. Шукана

                                                                                                                                0,         x  2,



емпірична функція розподілу має вид_{F(x) } ^_^{0,2,  2  x  3,}.

                                                                                                                               _0,7,   3  x  6,

                                                                                                                              1,        x  6

Правильна відповідь: (а).

4.5. Чому дорівнює незміщена оцінка дисперсії, якщо вибіркова дисперсія, що обчислена за вибіркою об’ємом 15 спостережень дорівнює 28?

а) 25;

б) 29;

в) 30.

Для вибірки _x1, _x2,..., _xn отриманої з генеральної сукупності, вибіркова дисперсія, яка обчислюється за формулою _{DX } ¹n _iⁿ1 _x  _x² , є зміщеною оцінкою дисперсії генеральної сукупності. Незміщена оцінка дисперсії генеральної сукупності шляхом добутку_DX на коефіцієнт зміщення дорівнює

^*                  n                   15

D_X    D_X   28  30. n 1       151

Правильна відповідь: (в).

4.6. Точкова оцінка математичного очікування нормального розподілення дорівнює 7. тоді його інтервальна оцінка може бути: а) (6,7; 10,7);

б) (7; 8,2);

в) (5,7; 8,3).

Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервалу, що покриває оцінюючий параметр. Довірчий інтервал – це інтервал, який з заданою надійністю _p покриває заданий параметр. Довірчий інтервал для математичного очікування записується у вигляді x_aˆ  _    x_aˆ  _, де  - оцінюючий параметр, математичне очікування генеральної сукупності; _xaˆ - вибіркове середнє значення, точкова оцінка математичного очікування; _ - гранична помилка довірчого інтервалу. Таким чином, довірчий інтервал – симетричний відносно вибіркового середнього, величина відхилення дорівнює _ : _xaˆ  _. Розглянемо перший інтервал (а), знайдемо величину _ : 7  6,7  0,3; 10,7  7  3,7 . Отримали різні граничні помилки, відповідь (а) не підходить. Другий довірчий інтервал (б) не підходить, оскільки нижня границя довірчого інтервалу співпадає з вибірковою оцінкою параметра. Для третього інтервалу (в) гранична помилка

_ : 7 5,7 1,3; 8,3 7 1,3. Довірчий інтервал можна представити у вигляді

(7 1,3).

Правильна відповідь: (в).

5.   Тестові завдання для самоперевірки

5.1. Задані          множини A {1,3,4},   B {2,3,1,4}.          Тоді для   них   буде неправильним наступне твердження:

а) множина А є підмножиною множини В;

б) множини А,В перетинаються;

в) множина А не дорівнює множині В;

г) А та В не мають спільних елементів.

5.2. Одночасно підкидають дві монети. Подія А={перший раз випав герб}, В={обидва рази випали цифри}. Тоді правильним для цих подій буде наступне твердження:

а) подія А тотожна події В; б А та В не мають спільних елементів; в) події А та В несумісні;

г) А та В перетинаються.

5.3. Ймовірність, що кубик впаде на грань «4» при умові, що випаде число очок більше двох, дорівнює:

а) 1 ;

6

б) 1 ;

4

в) 1 .

3

5.4. Електричний ланцюг має вид, як на малюнку.

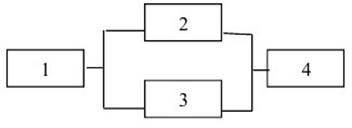
Подія _Ak = {елемент з номером к вийшов з ладу}, _k _1,2,3,4. Як записується подія В= {розрив ланцюга} в алгебрі подій _Ak ?

а) B  A₁  A₂  A₃  A₄ ; б B  A₁  A₂  A₃  A₄ ;

в) B  A₁ (A₂  A₃)  A₄ .

5.5. Скільки різних двозначних чисел можна скласти з цифр 1, 2, 3, 4, 5, 6, якщо всі цифри різні?

а) 20;

б) 30;

в) 36.

5.6. В урні лежить 3 білих та 5 чорних куль. Ймовірність вибору першою чорну кулю, а другою – білу дорівнює:

а) 3;

28

             б) 15     ;

56

              в) 8      .

15

5.7. Випадкова величина Х визначена на відрізку [-11; 27]. Чому дорівнює ймовірність P(7  X) ?

а) 34;

38

              б) 20      ;

37

              в) 25      .

38

5.8. Кількість перестановок у слові «МИР» дорівнює: а) 6;

б) 9;

в) 16.

5.9. Найбільш ймовірним числом появи герба при 4 підкиданнях монети є:

а) 3 та 2;

б) 4;

в) 3.

5.10. Перший завод випускає якісні верстати з ймовірність 0,8; другий завод – 0,7. На кожному заводі придбали по одному верстату. Ймовірність того, що вони обидва якісні, дорівнює:

а) 0,87;

б) 1,5;

в) 0,56.

5.11. Одночасно підкидають чотири монети. Яка ймовірність того, що всі монету випадуть однією стороною?

а) 0,0005;

б) 0,125;

в) 0,25.

5.12. Одночасно підкидають 4 кубика. Яка ймовірність того, що сума очок на кубиках менше 4?

а) 0;

б) 0,895;

в) 1.

5.13. Скільки існує способів вибору трьох карт з колоди у 36 карт, так, щоб серед них був один туз?

а) 1244;

б) 1984;

в) 686.

5.14. Скільки існує чотиризначних чисел, у записі яких немає парних цифр?

а) 294;

б) 625;

в) 1584.

5.15. Одночасно викидається 4 гральних кубика. Скільки можливо різних результатів цього випробування)?

а) 1024;

б) 1296;

в) 1684.

5.16. Чому дорівнює ймовірність того, що з двох перевірених деталей  хоча б одна виявиться стандартною, якщо ймовірність брака однієї деталі складає 0,1?

а) 0,2;

б) 0,99;

в) 0,96.

5.17. Маємо три партії деталей по 15 деталей в кожній. Кількість стандартних деталей в першій, другій та третій партіях відповідно дорівнює 11, 13, 12. яка ймовірність, що навмання обрана деталь виявиться бракованою?

а) 4;

15

             б) 11     ;

15

             в) 12      .

15

5.18. Дискретна випадкова величина Х має закон розподілення ймовірності

Чому дорівнює значення математичного очікування _M(X) ? а) 2,1;

б) 3,6;

в) 5,1.

5.19. Дискретна випадкова величина Х має закон розподілення ймовірності

Чому дорівнює значення дисперсії _D(X) ?

а) 15,2;

б) 10,24;

в) 4,96.

5.20. Як записується емпірична функція розподілення для вибіркової випадкової величини, що задана у вигляді статистичного ряду?

                                          0,    x  1,



                                         0,2,   1  x  2,

          а) F(x)  0,4, 2  x  5, ;

^0,6,          5  x  6, 

                                       1,    x  6

                                          0,    x  1,



                                          0,2,   1  x  2,

^

              б) F(x)  0,6,    2  x  5,;

^0,9,          5  x  6, 

                                       1,    x  6

                                          0,    x  1,



                                          0,2,   1  x  2,

          в) F(x)  0,4, 2  x  5,

^0,3,          5  x  6, 

                                      0,1,    x  6

5.21. Нехай Х – випадкова величина з функцією розподілення:

                                                                                                          0,    x  0,



                                                                                                         0,3,    0  x  2,



                                                                                     F(x)  0,8,   2  x  5,

^0,9,          5  x  8, 

                                                                                                       1,    x  8

Як можна представити закон розподілення випадкової величини Х у вигляді таблиці?

а)

б)

в)