Методичні вказівки до виконання графічних робіт. Креслення. Розділ "Нарисна геометрія".
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ВІННИЦЬКИЙ КОЛЕДЖ НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ ХАРЧОВИХ ТЕХНОЛОГІЙ
КРЕСЛЕННЯ
РОЗДІЛ «НАРИСНА ГЕОМЕТРІЯ»
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ГРАФІЧНИХ РОБІТ ПІДВИЩЕНОЇ СКЛАДНОСТІ
![]()
Вінниця, 2013
Методичні вказівки до виконання графічних робіт підвищеної складності з навчальної дисципліни «Креслення», розділ «Нарисна геометрія». Методична розробка.
Укладач: Мусієнко Л.П., спеціаліст першої категорії, викладач загальнотехнічних дисциплін Вінницького коледжу НУХТ.
Рецензент: Мельник О.П., доцент кафедри інженерної та комп'ютерної графіки ВНТУ, кандидат технічних наук.
![]()
Ухвалено на засіданні навчально-методичної ради Вінницького коледжу НУХТ Протокол №4 від 09.04.2013 р.
Голова навчально-методичної ради
__________ Н.М. Данильченко
![]()
РЕЦЕНЗІЯ
на методичну розробку викладача Вінницького коледжу НУХТ Мусієнко Лариси Петрівни
“Методичні вказівки до виконання графічних робіт підвищеної складності з навчальної дисципліни «Креслення», розділ «Нарисна геометрія»”
Методична розробка складається з вступу, детальної послідовності виконання кожного завдання та варіантів завдань. Кожне завдання має свою мету, короткі теоретичні відомості та зразки виконання завдань. Методична розробка виконана на належному методичному рівні. Всі пояснення до завдань викладено на доступному рівні.
Завдання складені в послідовності, що відповідає теоретичному матеріалу в підручнику. Методична розробка охоплює наступні розділи: “Графічне оформлення креслень”, “Основи нарисної геометрії та проекційне креслення”.
![]()
Виконання студентами вправ підвищеної складності сприяє більш глибокому і міцному засвоєнню матеріалу, розвиває просторову уяву, зорову пам’ять та послідовність дій, допомагає набути навики у виконанні креслень.
Методична розробка оформлена правильно і може бути рекомендована для використання в навчальному процесі.

З М І С Т
1. Вступ…………………………………………………………….....5
2. Графічне завдання №1……………………………………………6
3. Графічне завдання №2…………………………………………..13
4. Графічне завдання №3…………………………………………..17
5. Графічне завдання №4…………………………………………..21
6. Графічне завдання №5…………………………………………..23
7. Список використаних джерел…………………………………..27
8. Додаток А. Варіанти завдань до виконання графічного
![]()
![]()
![]() завдання №1……………………………………………………..28
завдання №1……………………………………………………..28
9. Додаток Б. Варіанти завдань до виконання графічного
завдання №2…………………………………………………….34
10. Додаток В. Варіанти завдань до виконання графічного
завдання №3……………………………………………………..39
11. Додаток Г. Варіанти завдань до виконання графічного
завдання №4……………………………………………………..44
12. Додаток Д. Варіанти завдань до виконання графічного
завдання №5……………………………………………………..49
ВСТУП
![]()
![]()
![]() Методичні вказівки містять
пояснення до виконання п’яти графічних завдань підвищеної складності. Мета
кожного графічного завдання - засвоєння знань студентами з окремих тем
навчальної дисципліни «Креслення», розділу «Нарисна геометрія». Рекомендовано виконати
такі графічні завдання:
Методичні вказівки містять
пояснення до виконання п’яти графічних завдань підвищеної складності. Мета
кожного графічного завдання - засвоєння знань студентами з окремих тем
навчальної дисципліни «Креслення», розділу «Нарисна геометрія». Рекомендовано виконати
такі графічні завдання:
• Аналіз багатогранника.
• Пряма та площина. Позиційні задачі.
• Побудова проекцій лінії взаємного перетину двох поверхонь методом січних площин.
• Побудова проекції лінії взаємного перетину двох поверхонь методом січних сфер.
• Побудова проекцій лінії взаємного перетину поверхні площиною загального положення або площиною окремого положення.
Кожному студенту пропонується виконати свій варіант. Завдання до графічних робіт 1–5 вибирається з додатків А–Д. Крім методичних вказівок студент повинен ознайомитись з рекомендованою літературою, лекціями та посібником, що стосуються певної теми.
Всі графічні завдання слід виконувати олівцем на аркуші паперу формату А3, а відповідні надписи шрифтом № 5 або за допомогою конструкторського редактору КОМПАС-ГРАФІК. Перед виконанням
кожного завдання для наочності зображень, які будуть виконуватись, необхідно провести відповідне компонування креслення. Приклади оформлення кожного графічного завдання також містяться в даній розробці.
Графічні роботи призначені для виконання студентами ВК НУХТ спеціальності 5.07010602 «Обслуговування та ремонт автомобілів і двигунів». Рекомендовано до виконання на заняттях гуртка з креслення.
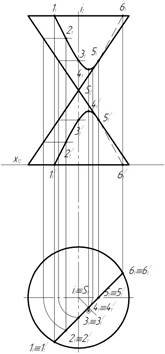
 1 ГРАФІЧНЕ ЗАВДАННЯ № 1
1 ГРАФІЧНЕ ЗАВДАННЯ № 1
Умова: Для заданого багатогранника (рис.1) потрібно:
1. За двома заданими (фронтальною та горизонтальною) побудувати третю (профільну) проекцію;
2. Визначити положення ребер та граней відносно
площин проекцій та записати в запропоновану таблицю;
3. Визначити взаємне положення ребер та граней та записати по дві пари (якщо вони є) в таблицю;
4.
![]()
![]()
![]() Визначити сліди (горизонтальний та фронтальний) одного з
ребер та площини загального положення.
Визначити сліди (горизонтальний та фронтальний) одного з
ребер та площини загального положення.
Мета завдання. Розвиток просторової уяви за ортогональними проекціями багатогранника, засвоєння теоретичного матеріалу на конкретному прикладі.
Послідовність виконання
1. За двома заданими проекціями (фронтальною та горизонтальною) будують третю (профільну) проекцію багатогранника. В першу чергу позначають латинськими великими буквами всі вершини.
2. Виконують аналіз ребер многогранника. Ребро многогранника уявляють як відрізок прямої. Для цього слід звернути увагу на класифікацію прямих та їх означення. Також потрібно знати зображення ребер на епюрі, їх ознаки та характерні особливості. З цією метою студенту пропонується ознайомитися з табл. 1,2 та рис. 2, в яких для прямих окремого положення виділяються зазначені позиції.
3. Виконують аналіз граней многогранника. Кожна грань являє собою площину. Звернути увагу на основні означення, класифікацію площин, зображення площин на епюрі, їх характерні особливості та ознаки, корисною для цього будуть табл. 3, 4 та рис. 3.
4. Визначають взаємне положення ребер та граней многогранника, враховуючи властивості проекцій пар ребер або граней. Для визначення взаємного положення ребер слід мати на увазі, що ребра в просторі можуть бути мимобіжними, паралельними або перетинатись. Мимобіжними грані, на відміну від паралельних, бути не можуть, оскільки при продовженні їх вони будуть перетинатися.
5. Для одного з ребер загального положення будують горизонтальні М1, N1, фронтальні М2, N2 проекції горизонтального М та фронтального слідів N. Слід ребра - це точка перетину ребра а площинами проекцій. Тому для горизонтального сліду ребра його горизонтальна проекція М1 збігається з самим слідом М, а фронтальна проекція М2 буде знаходитись на осі X (рис.1). У фронтального сліду фронтальна проекція N2 збігається з самим слідом N, а горизонтальна проекція N1 знаходиться на осі X як точка, яка належить площині проекцій П2.
6. Правильно підписують графічне завдання. Зразок виконаного завдання показано на рис.2 , а індивідуальні завдання наводяться в додатку А.
![]()
![]()
![]()
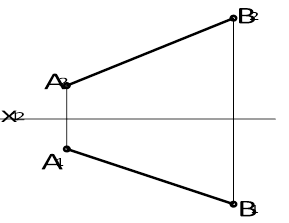
Рисунок 1. Креслення прямої загального положення

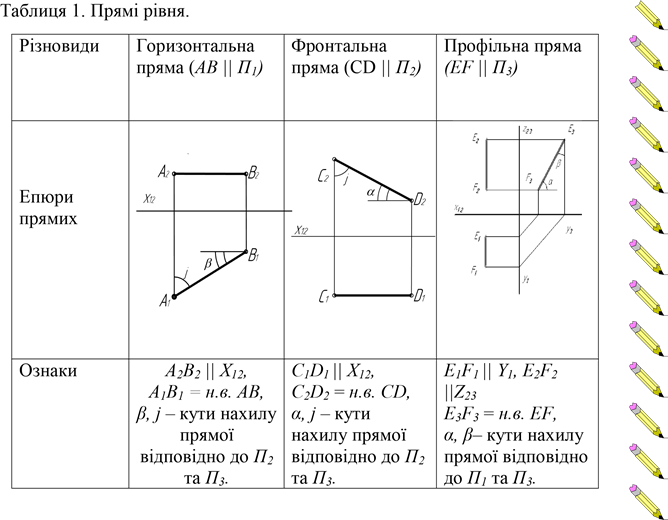
Таблиця 2. Проекціювальні прямі.

Таблиця 3. Площини рівня.

Таблиця 4. Проекціювальні площини.

Рисунок 3 – Площина загального положення
2. ГРАФІЧНЕ ЗАВДАННЯ №2
Умова: Для заданої площини розв’язати такі позиційні задачі (рис. 4):
1) побудувати пряму, паралельну заданій площині;
2) побудувати площину, паралельну заданій площині; 3) побудувати пряму, яка перетинає задану площину; 4) побудувати площину, яка перетинає задану площину.
Мета завдання: Закріпити на практиці набуті теоретичні знання щодо побудов прямих та площин, паралельних заданій, побудов точки перетину прямої з площиною та двох площин. В двох останніх випадках слід вміти визначати видимість прямої, що перетинає площину, та двох площин, що перетинаються.
Послідовність виконання
1. Оскільки графічне завдання полягає в розв’язуванні чотирьох задач, то формат аркуша паперу А3 ділять умовно на 4 рівних частини та 4 рази креслять в 2-х проекціях заданий варіант площини. З теорії відомо, що площина має шість способів її задання. Табл. 5 ілюструє ці способи задання і є корисною для вміння задавати площину одним із способів.
2.
![]()
![]()
![]() Виконують побудову прямої l, паралельної площині
(задача 1), що задана, наприклад слідами (ho
f o). Розв’язок задачі випливає
із означення паралельності прямої і площини: пряма паралельна площині, якщо
вона паралельна прямій, яка знаходиться в цій площині. Для цього попередньо в
площині
побудована довільна пряма m, що належить площині. Потім через
довільну т. С проводять пряму l , яка паралельна прямій m0.
Здійснюють символьний запис: l // (ho f o).
Виконують побудову прямої l, паралельної площині
(задача 1), що задана, наприклад слідами (ho
f o). Розв’язок задачі випливає
із означення паралельності прямої і площини: пряма паралельна площині, якщо
вона паралельна прямій, яка знаходиться в цій площині. Для цього попередньо в
площині
побудована довільна пряма m, що належить площині. Потім через
довільну т. С проводять пряму l , яка паралельна прямій m0.
Здійснюють символьний запис: l // (ho f o).
3. Виконують побудову площини , паралельної заданій , яка, наприклад, задана двома паралельними прямими (а // в). Розв’язування задачі починають, виходячи із означення: якщо дві прямі однієї площини, що перетинаються, паралельні двом прямим другої площини, що перетинаються, то ці площини паралельні між собою. Спочатку в площині (а // в) довільно проведені дві прямі, які перетинаються с d. Потім через будь-яку точку, що знаходиться в першому октанті, наприклад т. А, проводять дві прямі, що перетинаються (m n), які є відповідно паралельними с d. Здійснюють символьний запис: (а // b) // (c d).
4. Виконують побудову прямої l , що перетинає площину ∑, яка, наприклад, задана трикутником АВС. Проекції прямої загального положення проводять довільно. Далі використовують алгоритм побудови, прямої з площиною. А саме:
4.1. Через будь-яку проекцію прямої l, проводять додаткову проекцію-
вальну площину (тут використовують горизонтальну проекцію l1, тобто

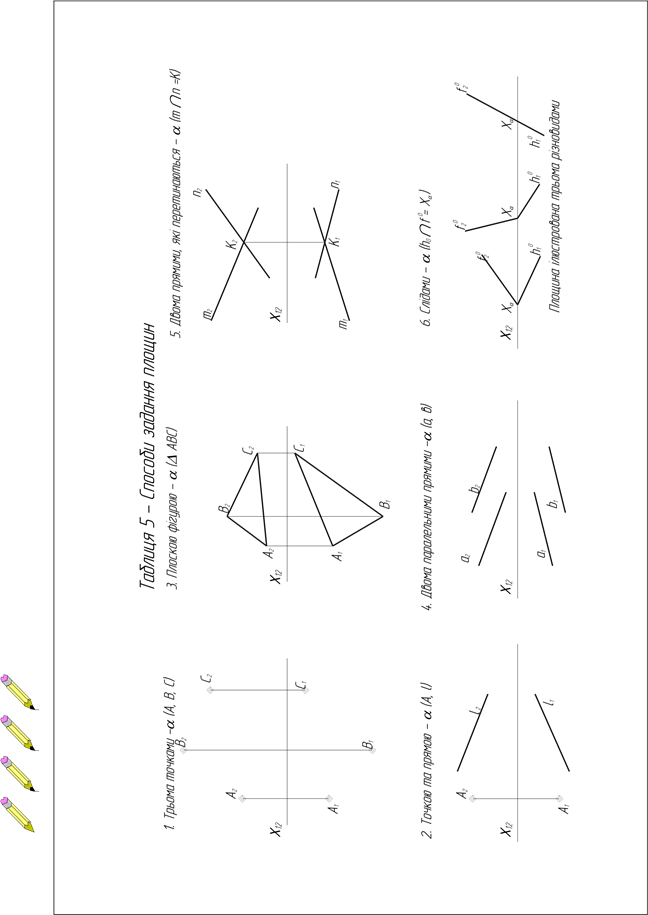
вводять горизонтально-проекціювальну площину).
4.2. Визначають лінію перетину m (m1, m2) додаткової площини з заданою (АВС). Лінія m визначається точками 1 та 2, тобто m [1, 2]. 4.3. Фіксують в даному випадку фронтальну проекцію точки перетину К (К2) як результат перетину здобутої прямої m (m2) та заданої l, (l2), тобто m2 l2 = К2. Відсутню проекцію К1 шуканої точки К знаходять за проекційним зв’язком на П1, тобто К1 l 1, m1 (l 1 m1).
4.4. Визначають видимість проекцій прямої l на П1 та П2. При цьому для визначення видимості горизонтальної проекції прямої l використовують точки 2 та 3, що конкурують на П1, а для визначення видимості фронтальної проекції l2 використовують точки 4 та 5, що конкурують на П2.
5. Виконують побудову площини (c // d), що перетинає задану (А, l). В даному випадку задача ілюструється на прикладі двох площин
(задається т. А та прямою l) та (довільно вводиться одним із способів, наприклад, паралельними прямими). Далі використовують алгоритм побудови двох площин. А саме:
5.1. Проводять першу допоміжну горизонтальну площину (допоміжні площини, як правило, беруть окремого положення).
5.2. Будують лінії перетину допоміжної площини з даними та . Площина перетинає площину по прямій c, а площину - по прямій d.
5.3.
![]()
![]()
![]() Перетин отриманих ліній с та d визначає
спільну точку перетину Е, яка на горизонтальній площині проекцій
фіксується як перетин с1 d1
= Е1, а фронтальна проекція т. Е знаходиться за
проекційним зв’язком на відповідному сліді-проекції додатково введеної площини .
Перетин отриманих ліній с та d визначає
спільну точку перетину Е, яка на горизонтальній площині проекцій
фіксується як перетин с1 d1
= Е1, а фронтальна проекція т. Е знаходиться за
проекційним зв’язком на відповідному сліді-проекції додатково введеної площини .
5.4. Проводять другу допоміжну горизонтальну площину .
5.5. Будують лінії перетину допоміжної площини з даними та . Площина перетинає площину по прямій е (на П1 проекцію е1 прямої е проводять через т. 51 паралельно С1). Площина перетинає площину по прямій k (на П1 проекцію k1 прямої k проводять через т. 61 паралельно d1).
5.6. Перетин здобутих ліній е та k визначає спільну точку перетину F, яка на горизонтальній площині проекцій фіксується як перетин е1 k1 = F1, а фронтальна проекція т. F знаходиться за проекційним зв’язком на відповідному сліді-проекції додатково введеної площини .
5.7. Визначають видимість площин та , що перетинаються.
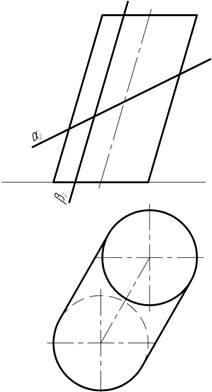
Умову до задач беруть в додатку Б, зразок виконаного епюра показано на рис. 4.
Примітка. З метою більш повного представлення способів задання площин зразок ілюструється, одночасно декількома способами задання площин. Студент у своєму конкретному завданні використовує лише один запропонований спосіб.
3. ГРАФІЧНЕ ЗАВДАННЯ №3
Умова: Побудувати переріз поверхні площиною загального положення. Виконати розгортку поверхні з нанесенням лінії перерізу. Визначити натуральну величину фігури перерізу (рис.5).
Мета завдання: Набуті теоретичні знання виявити на практиці при побудові перерізів різноманітних форм і розгорток та отримати необхідні навички на майбутнє при побудові розрізів та перерізів технічних деталей.
Послідовність виконання
Епюр в залежності від виду заданої поверхні може виконуватись на одному або двох аркушах формату А3. Мається на увазі, що другий аркуш формату А3 буде використовуватись для побудови розгортки поверхні в тому разі, якщо ця розгортка не поміститься разом з іншими побудовами до цього епюра.
1. Визначають положення січної площини та поверхні, що задані за умовою, та доцільність введення заміни площин проекцій: чи П2 на П4, чи П1 на П4. Наприклад, основа заданої поверхні паралельна до площини проекцій П1 або належить П1, то для спрощення побудов цю площину проекцій залишити без змін, а замінити П2 на нову П4.
2.
![]()
![]()
![]() Застосовують алгоритм перетворення
площини загального положення у проекціювальну способом заміни
площин проекцій та будують слід проекціювальної площини і положення
заданої поверхні для виконаного перетворення.
Застосовують алгоритм перетворення
площини загального положення у проекціювальну способом заміни
площин проекцій та будують слід проекціювальної площини і положення
заданої поверхні для виконаного перетворення.
3. Фіксують точки перетину проекціювальної площини з поверхнею.
Будують проекції лінії перерізу та визначають їх видимість на П1 та П2.
4. Будують натуральну величину фігури перерізу.
5.
![]() Виконують розгортку з
нанесенням лінії перерізу на ній. Також враховують, що місця згину на
розгортках показуються штрихпунктирною тонкою лінією з двома точками, а сам
розгортка позначається знаком .
Виконують розгортку з
нанесенням лінії перерізу на ній. Також враховують, що місця згину на
розгортках показуються штрихпунктирною тонкою лінією з двома точками, а сам
розгортка позначається знаком .
6. Записують шрифтом умову задачі, підписують графічне завдання.
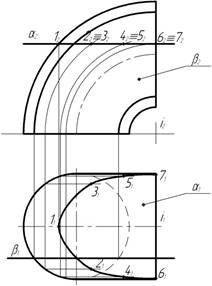
На рис. 5 показано розв'язування задачі, де площина загального положення перерізає циліндр, та його розгортка. Корисно при виконанні цього завдання звернутись до таблиць 6 і 7, повторити конічні перерізи та знати їх назви.
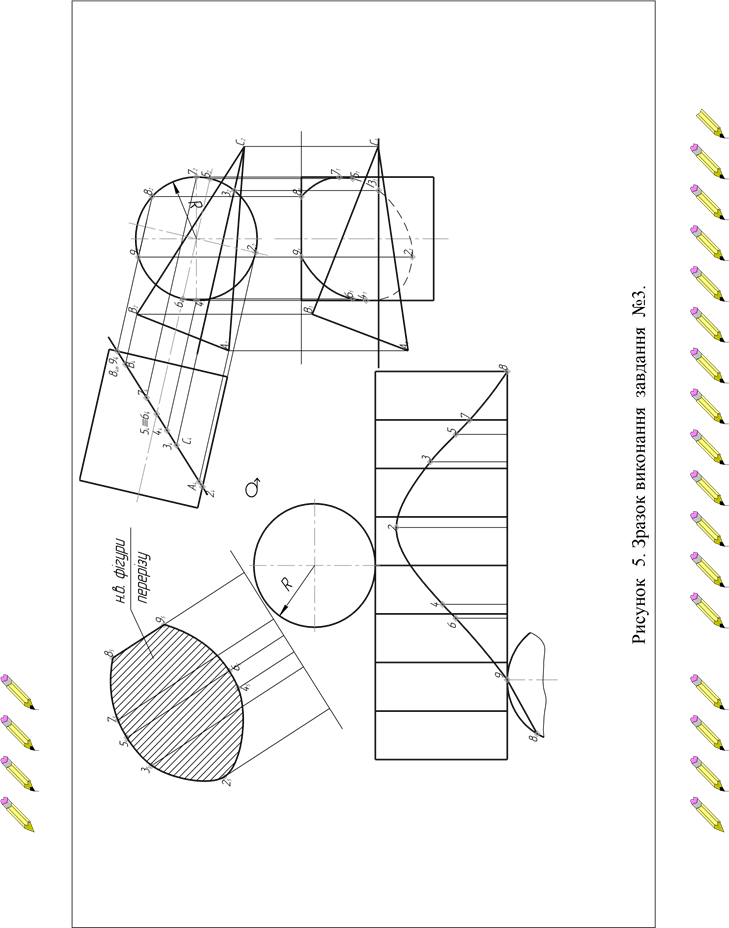
|
Таблиця 6 – Аналіз складності побудов перерізів |
|||
|
Сфера |
Тор закритий |
Тор відкритий |
Циліндр загального виду |
|
|
|
|
|
|
Зверніть увагу, як проходить січна площина, яка утворює більш простий переріз. Для циліндра загального виду побудуйте криві перерізу самостійно. |
|||

|
Таблиця 7 – Конічні перерізи |
|||||
|
|
Трикутник |
Коло |
Еліпс |
Парабола |
Гіпербола |
|
|
|
|
|
|
|
|
S |
l |
перерізає всі твірні |
l |
i |
|
|
Примітка: На завданнях для конуса обертання побудовано по дві поли. Для наочності побудови перерізів, частина поверхні, яка виділена тонкою суцільною лінією, не враховується. Визначіть криві перерізу, які потребують додаткових побудов, проаналізуйте їх складність. |
|||||


4. ГРАФІЧНЕ ЗАВДАННЯ №4
Умова: Побудувати дві проекції лінії взаємного перетину заданих поверхонь із застосуванням методу січних площин. Визначити видимість
(рис.6).
Мета завдання: Вміти на практиці визначати лінію взаємного перетину у випадку, коли технічна деталь складається із декількох поверхонь, які перетинаються.
Послідовність виконання
1. Визначають, які поверхні перетинаються, та встановлюють положення твірних (для поверхонь обертання) або ребер (для гранних поверхонь) відносно площин проекцій П1, П2, П3 .
2. Визначають, до якого випадку перетину (окремого або загального) можна віднести цю задачу. В окремому випадку перетину одна з поверхонь займає проекціювальне положення (твірні або ребра перпендикулярні до однієї з площин проекцій), в загальному випадку - проекціювальні ребра або твірні заданих поверхонь відсутні.
3.
![]()
![]()
![]() Застосовують алгоритм побудови точок на поверхні (в
окремому випадку перетину) або вибирають положення допоміжної площини (в
загальному випадку). Допоміжну січну площину вводять таким чином, щоб в
перетині з двома заданими поверхнями вона давала найбільш простий переріз.
Застосовують алгоритм побудови точок на поверхні (в
окремому випадку перетину) або вибирають положення допоміжної площини (в
загальному випадку). Допоміжну січну площину вводять таким чином, щоб в
перетині з двома заданими поверхнями вона давала найбільш простий переріз.
4. Будують лінії перетину допоміжної січної площини з кожною з двох заданих поверхонь. В місці перетину цих ліній визначають точки спільного перетину. Кожна з цих точок має потрійну належність поверхням, які перетинаються, та допоміжній січній площині.
5. Вводять ще декілька допоміжних січних площин з метою отримання точок, достатніх для побудови лінії взаємного перетину двох поверхонь.
6. З’єднують шукані точки, враховуючи їх видимість на поверхнях.
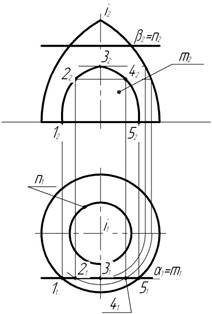
Зразки виконаних задач до завдання №4 показані на рис. 6, а індивідуальні завдання наводяться в додатку Г.
Примітка. З метою більш повного оволодіння методу січних площин зразок ілюструється, одночасно розв’язанням двох задач (одна з яких відноситься до окремих випадків перетину, друга – до загальних). Студент для свого конкретного варіанта розв’язує лише одну задачу.
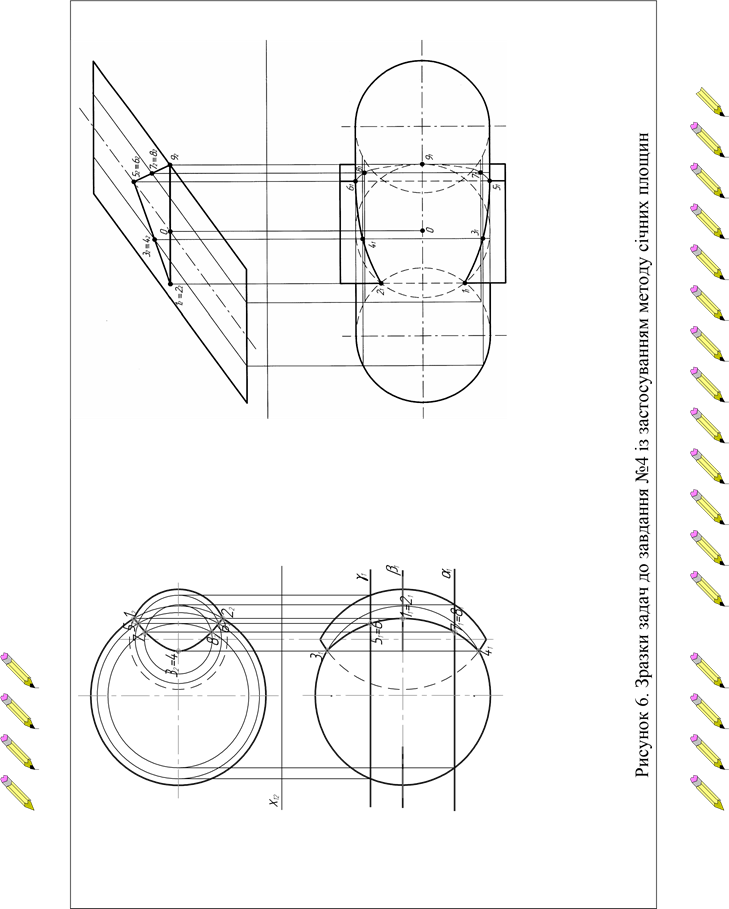
5. ГРАФІЧНЕ ЗАВДАННЯ № 5
Умова: Побудувати дві проекції лінії взаємного перетину заданих поверхонь із застосуванням методу січних сфер та визначити видимість. Мета завдання: Вміти для технічних деталей при побудові проекцій застосовувати метод січних сфер та теорему Монжа.
Послідовність виконання
1. ![]()
![]()
![]() Визначають,
які поверхні обертання перетинаються, як розташовані їх осі, чи можна
застосувати теорему Монжа. В деяких задачах для поверхонь, які перетинаються,
можливі варіанти застосування теореми Монжа. В цих випадках одна, з проекцій
лінії перетину має найпростіші побудови (рис. 7).
Визначають,
які поверхні обертання перетинаються, як розташовані їх осі, чи можна
застосувати теорему Монжа. В деяких задачах для поверхонь, які перетинаються,
можливі варіанти застосування теореми Монжа. В цих випадках одна, з проекцій
лінії перетину має найпростіші побудови (рис. 7).
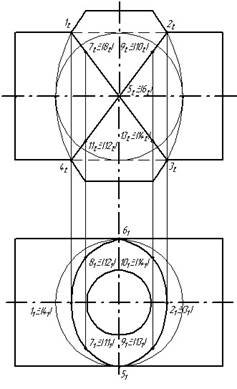
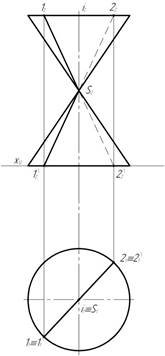
Рисунок 7. Варіант застосування теореми Монжа.
2. Визначають, які січні сфери (концентричні або ексцентричні) слід застосувати, щоб розв'язати запропоновану задачу.
2.1 Слід врахувати умови використання січних концентричних сфер (рис.8):
- поверхні, які перетинаються, є поверхнями обертання;
- осі поверхонь обертання перетинаються та знаходяться в площині симетрії, яка паралельна до однієї з площин проекцій.
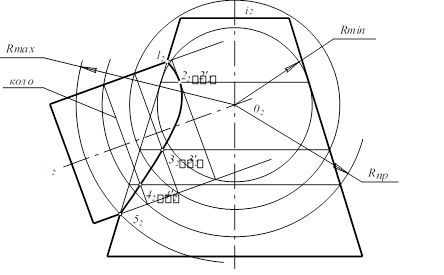
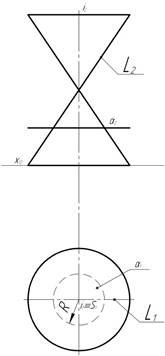
Рисунок 8. Побудова концентричних сфер.
![]()
![]()
![]()
У випадку застосування концентричних січних сфер на перетині прямолінійних осей обертання i, j знаходять спільний центр О, який надалі використовується для проведення концентричних сфер. Сфера мінімального радіуса R min визначає положення найглибших точок 2, 2´ і проводиться таким чином, щоб вона була вписана в одну з поверхонь (конус) та перетинала обрисові твірні іншої поверхні (циліндра). Сфера максимального радіуса R max має проходити через одну із характерних точок 5 (точки перетину обрисових твірних). Всі проміжні сфери мають значення радіуса R min < R пр < R max. Кожна введена концентрична сфера співвісна з заданими поверхнями і має найпростіший переріз з ним – коло, перетин яких дає спільні точки, наприклад 4, 4´, лінії взаємного перетину. Введення декількох концентричних сфер дозволяє побудувати сукупність точок 1; 2, 2´; 3, 3´; 4, 4´; 5, які визначають лінію перетину.
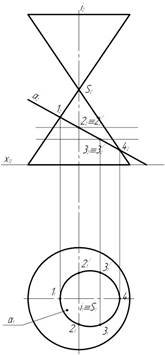
2.2 Якщо порушується одна з умов використання методу концентричних сфер, то слід проводити посередники-сфери, але з різних центрів. Спосіб, який використовується на підставі таких сфер, має назву ексцентричних сфер (рис. 10).
4. Визначають відсутні проекції точок перетину, з'єднують їх плавними кривими, враховуючи видимість кожної з них.
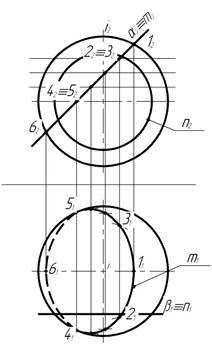
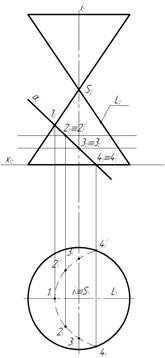
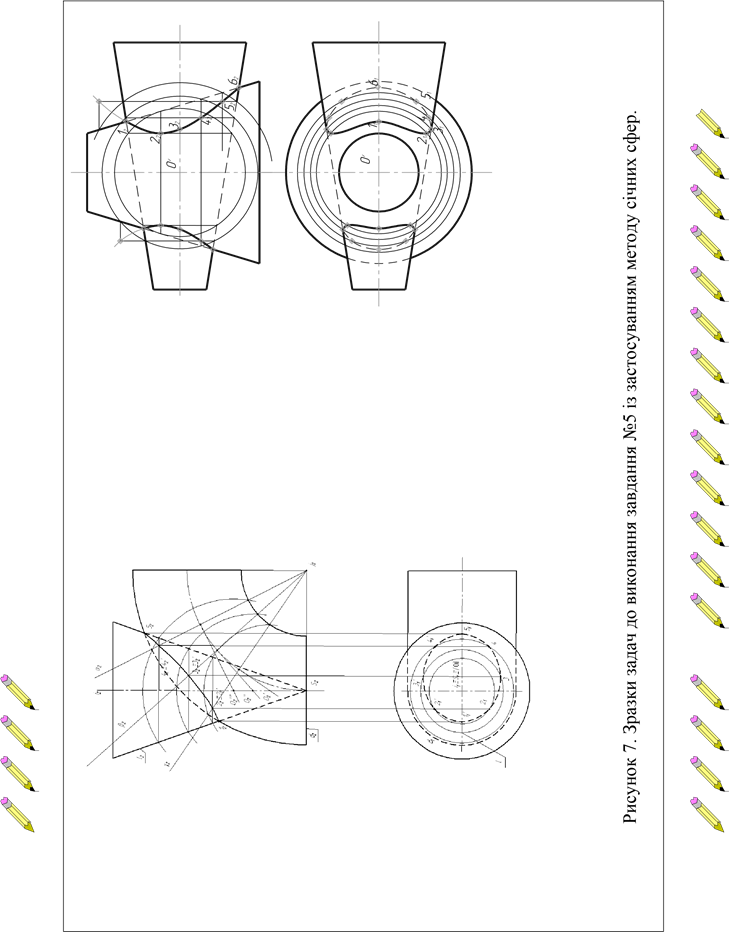
Зразок виконаного епюра, із застосуванням методу січних концентричних сфер, показаний на рис. 10, а індивідуальні завдання наведені в додатку Д.
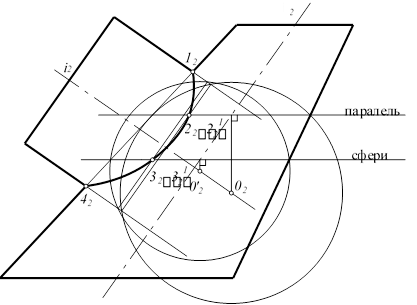
Рисунок 9. Побудова ексцентричних сфер.
![]()
Примітка. З метою більш повного оволодіння методу січних сфер зразок (рис.10) ілюструється, одночасно розв’язанням двох задач (одна з яких відноситься до методу концентричних сфер, друга – до методу ексцентричних сфер). Студент для свого конкретного варіанта розв’язує лише одну задачу.
 СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ.
1. Бубенников А. В., Громов М. Я. Начертательная геометрия. – М.: Высшая школа, 1985. – 416 с.
2. Гордон В. О., Семенцов-Огиевский М. А. Курс начертательной геометрии. – М.: Наука, 1988. – 270 с.
3. Гордон В. О., Иванов Ю. Б., Солнцева Т. Е. Сборник задач по курсу начертательной геометрии. – М.: Наука, 1973. – 351 с.
4. Кузнєцов Н. С. Начертательная геометрия. – М.: Высшая школа,
1981. – 496 с.
5. ![]()
Сборник задач по начертательной геометрии с элементами программирования / Под общей ред. Михайленко В. Е. – М.: Высшая школа, 1976. – 222 с.
6. Фролов С.А. Начертательная геометрия. – М.: Машиностроение,
1978. – 238 с.
7. Фролов С.А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1980. – 224 с.
8. Государственные стандарты единой системы конструкторской документации (ЕСКД).
ДОДАТКИ
![]()
![]()
![]()

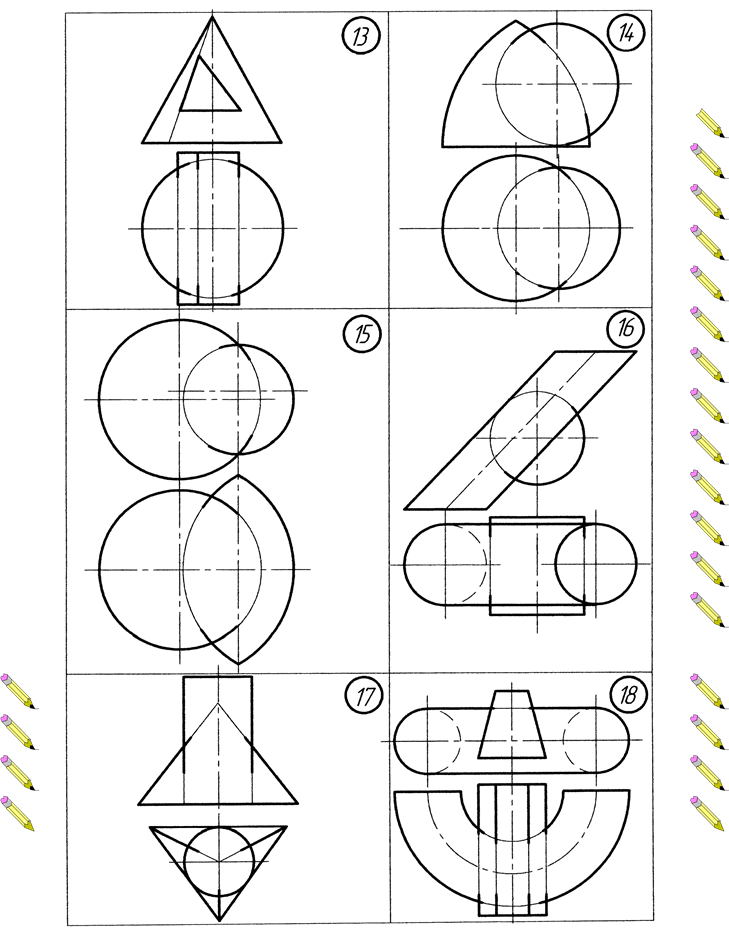
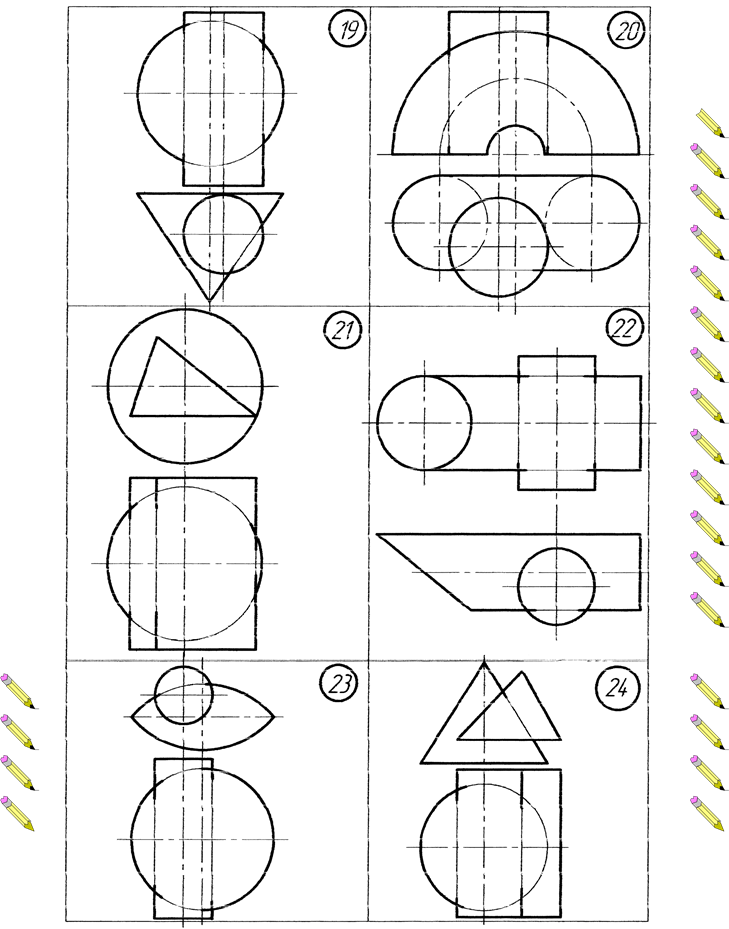
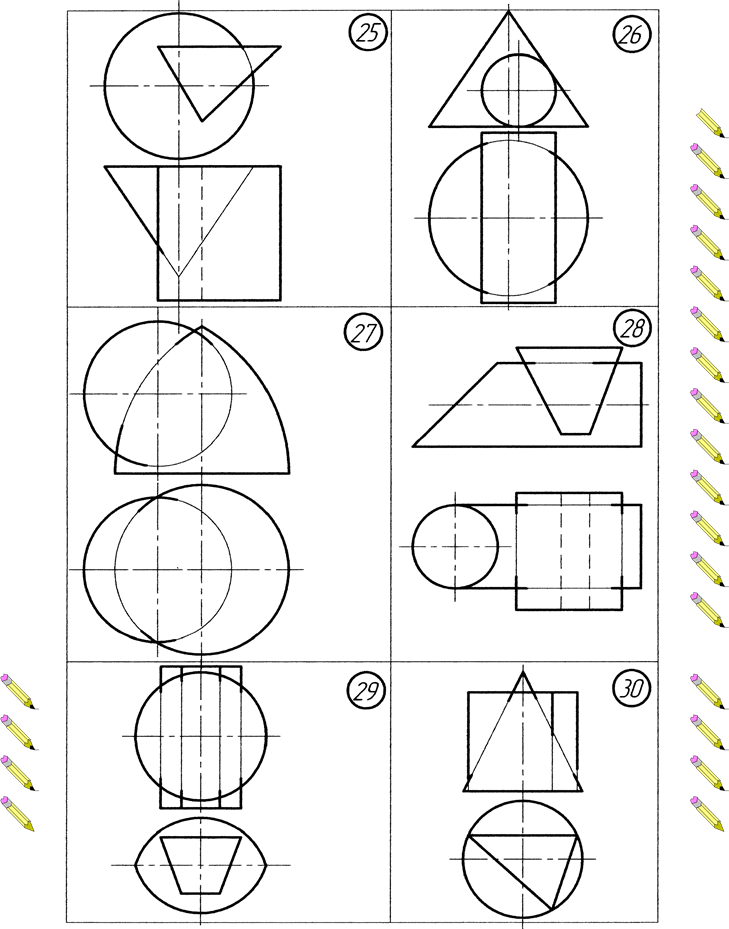
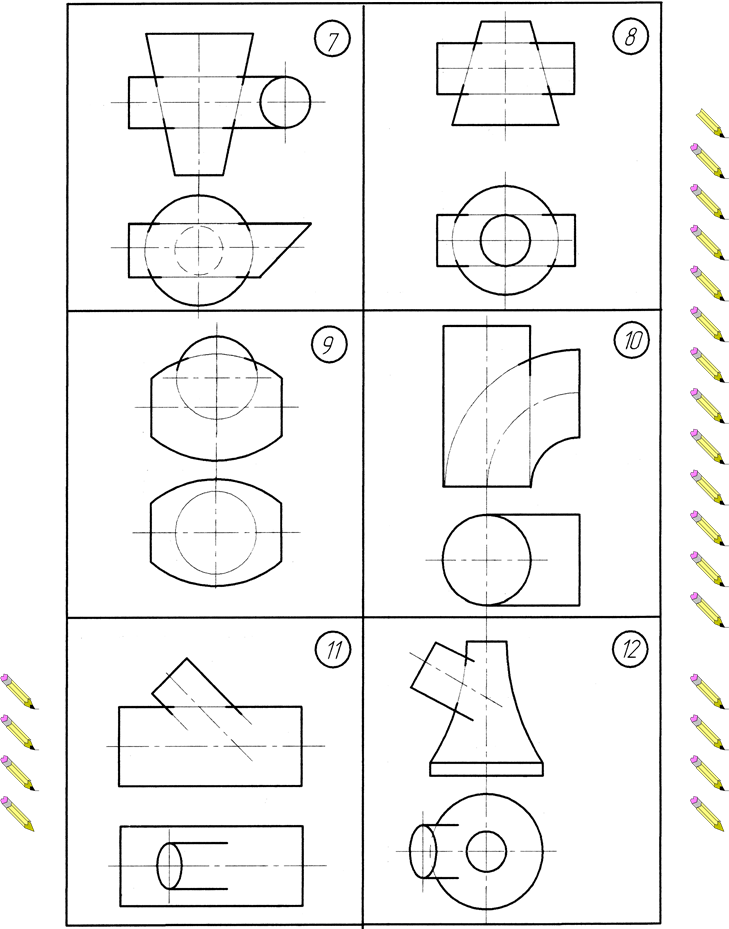
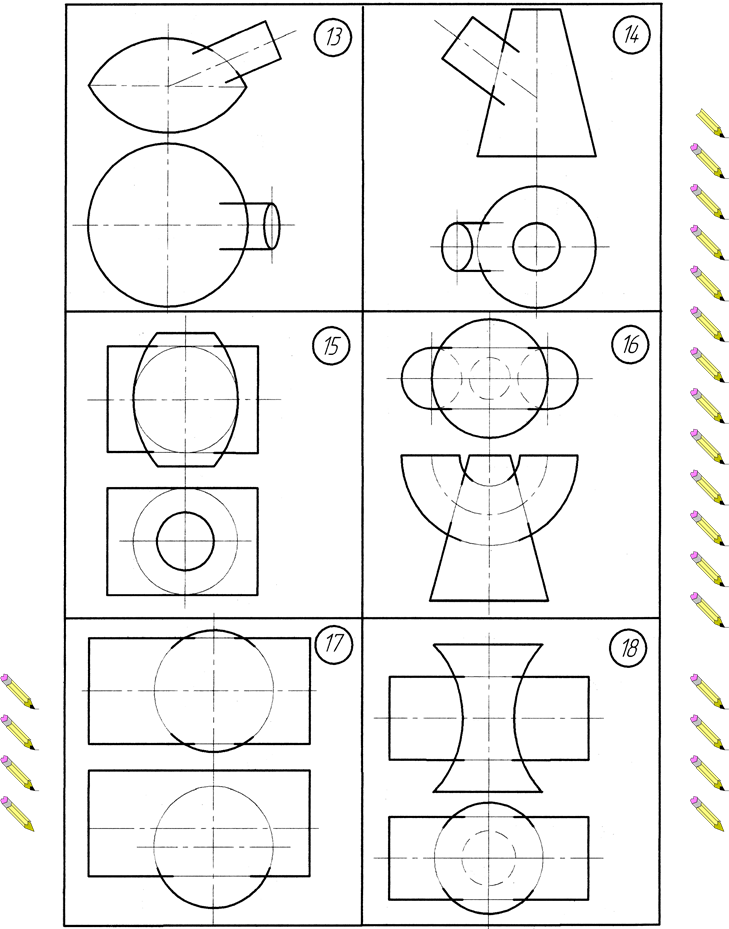
ВАРІАНТИ ЗАВДАНЬ Додаток А. Варіанти до виконання завдання №1
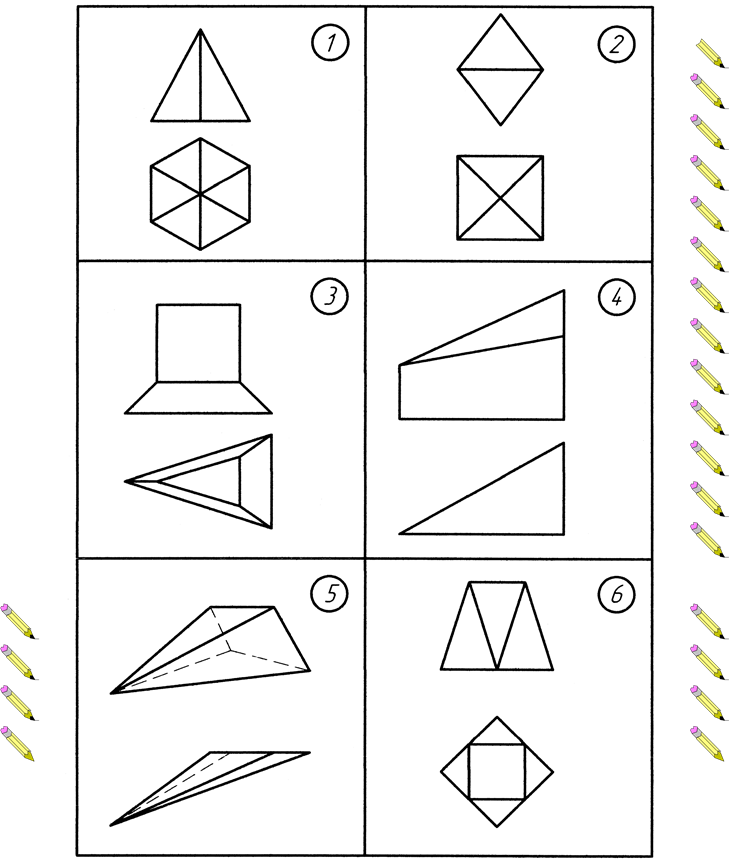
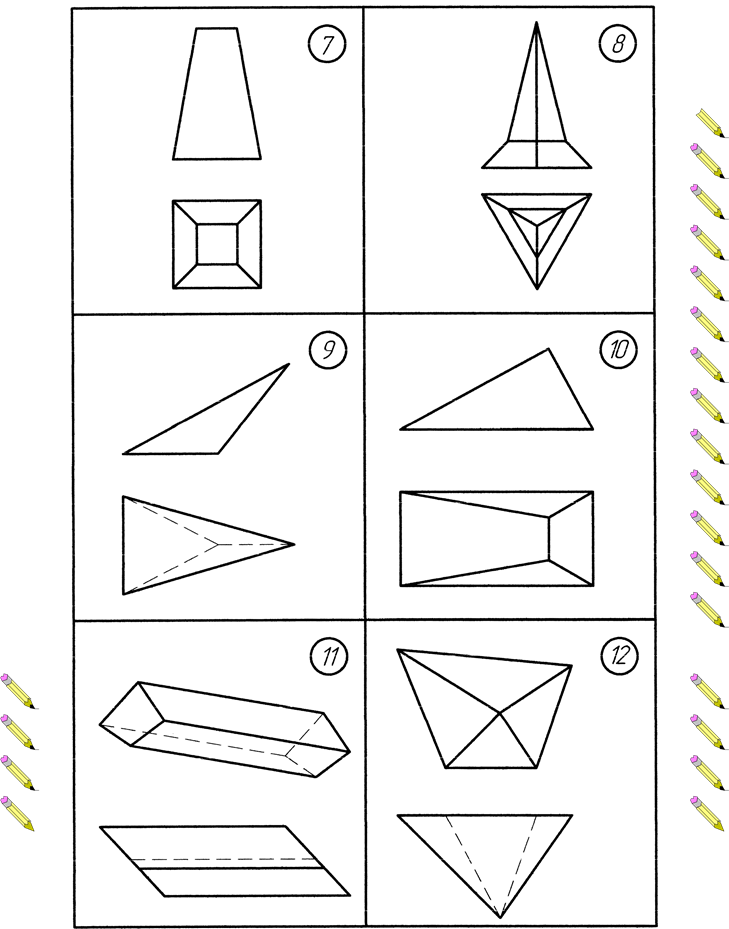
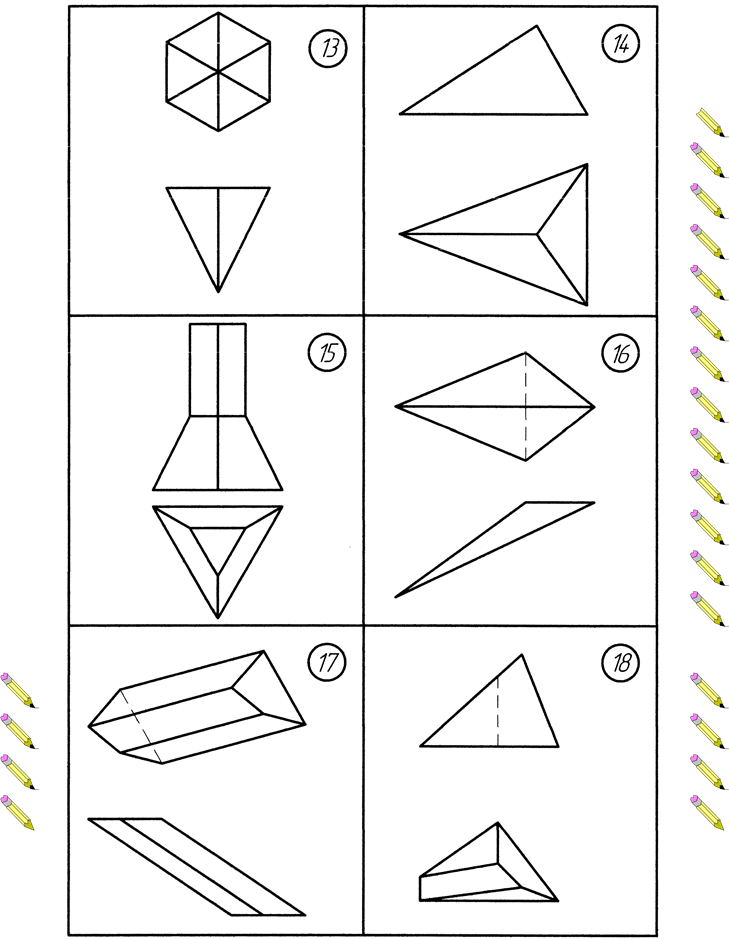
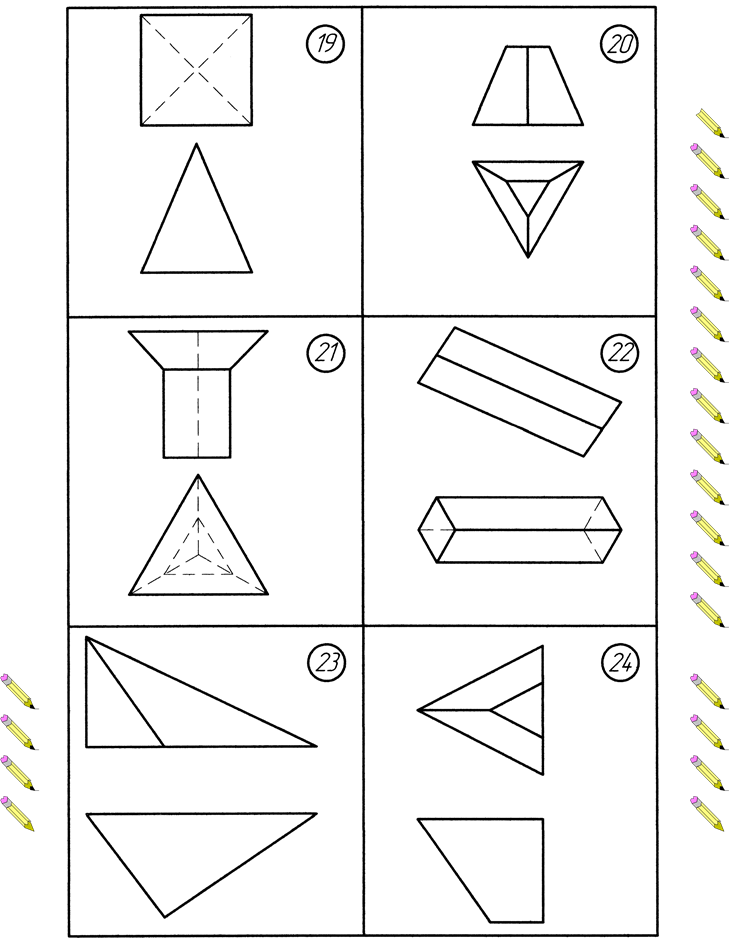
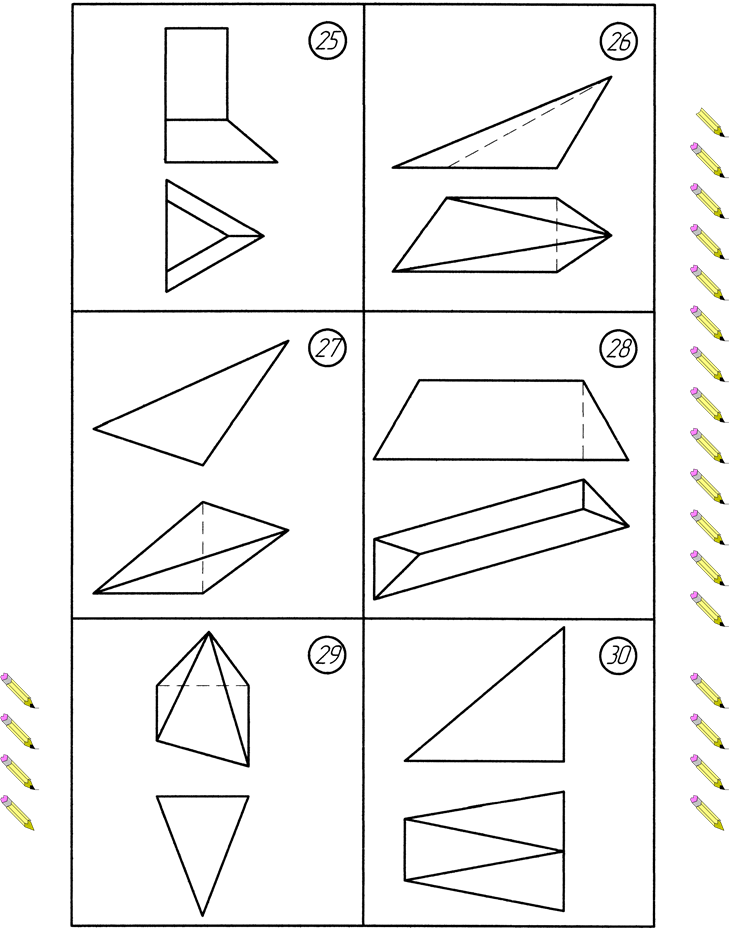
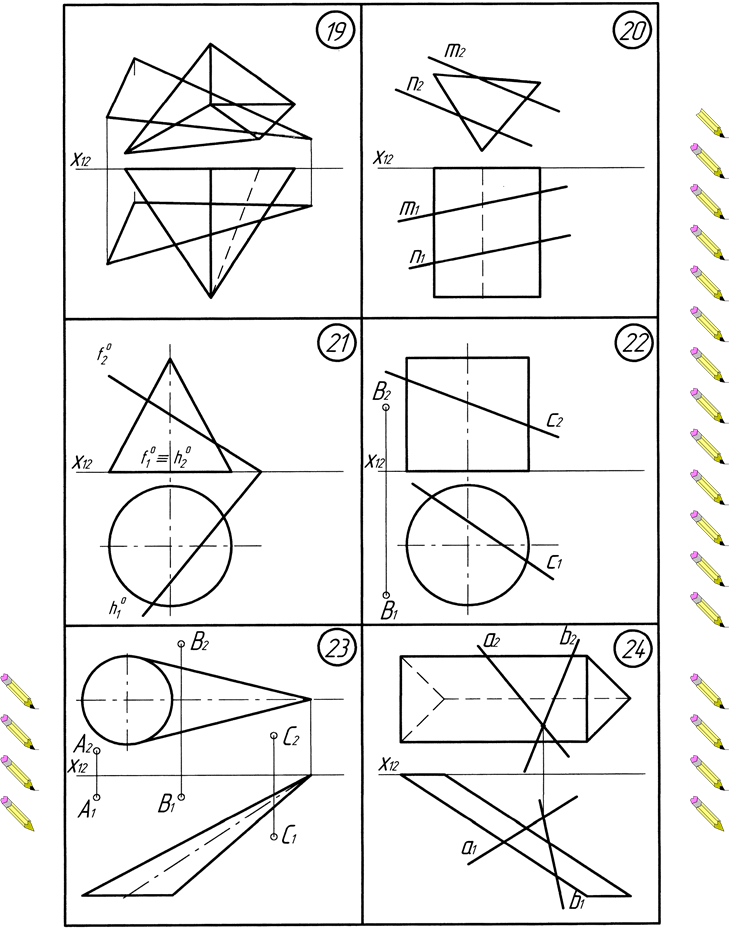
Додаток Б. Варіанти до виконання завдання №2
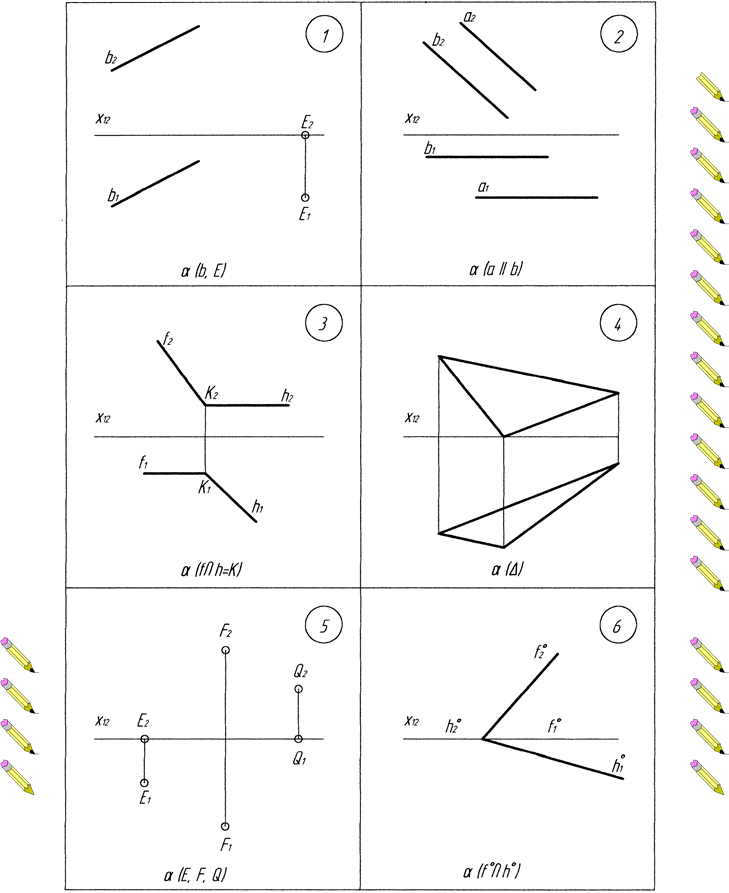

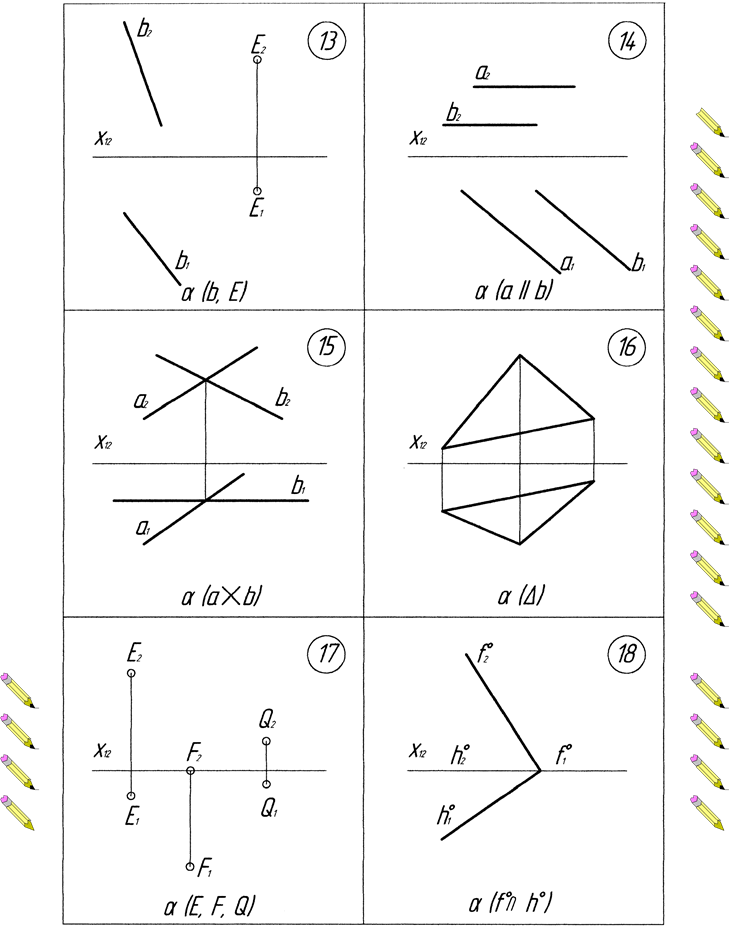
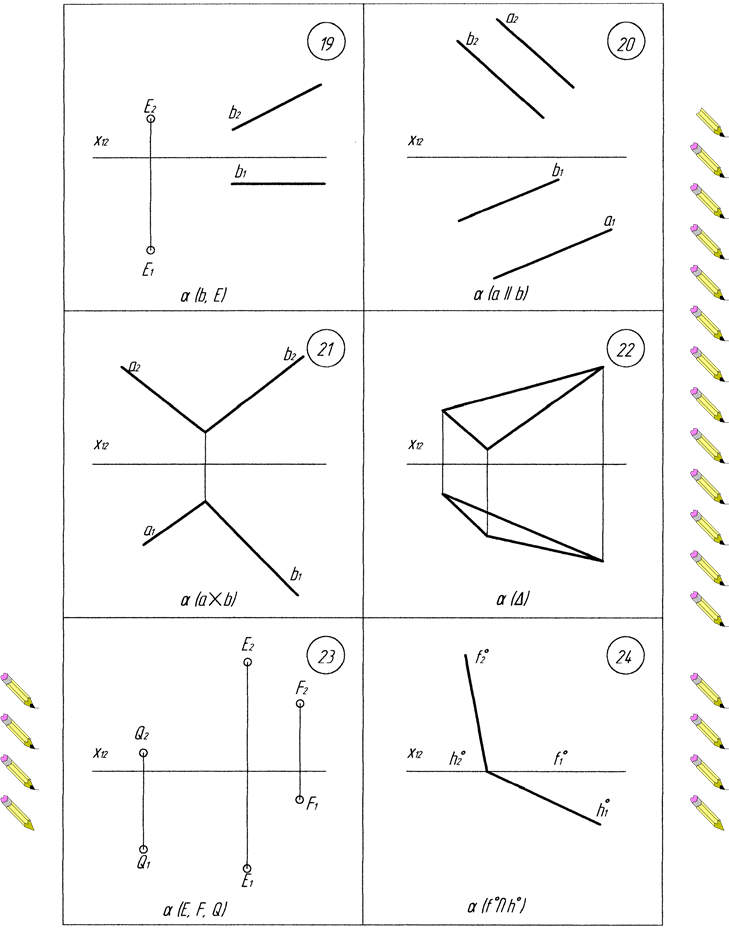
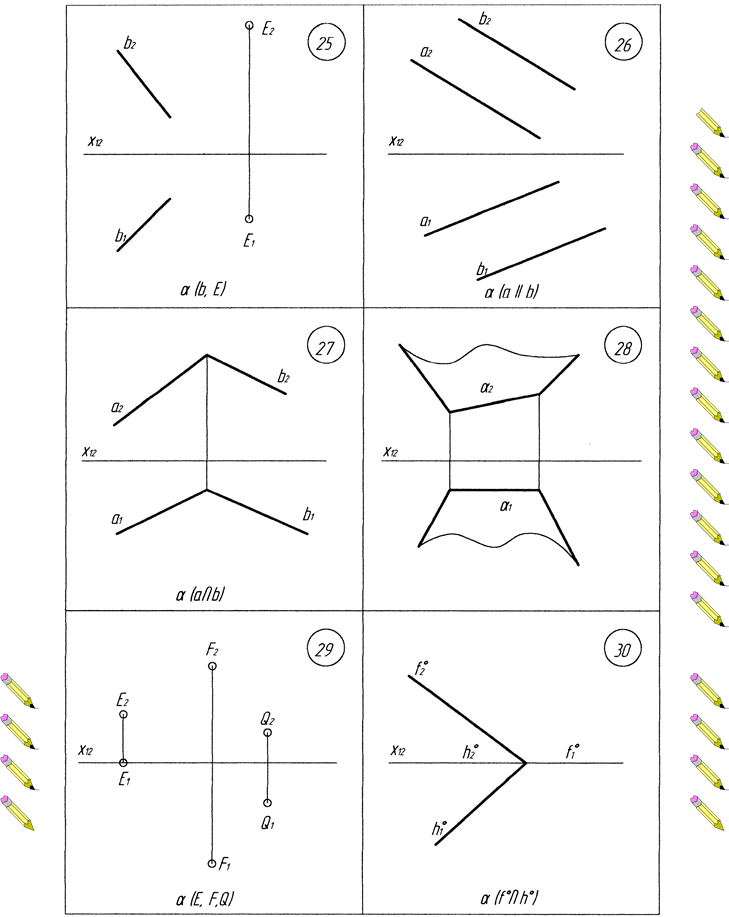
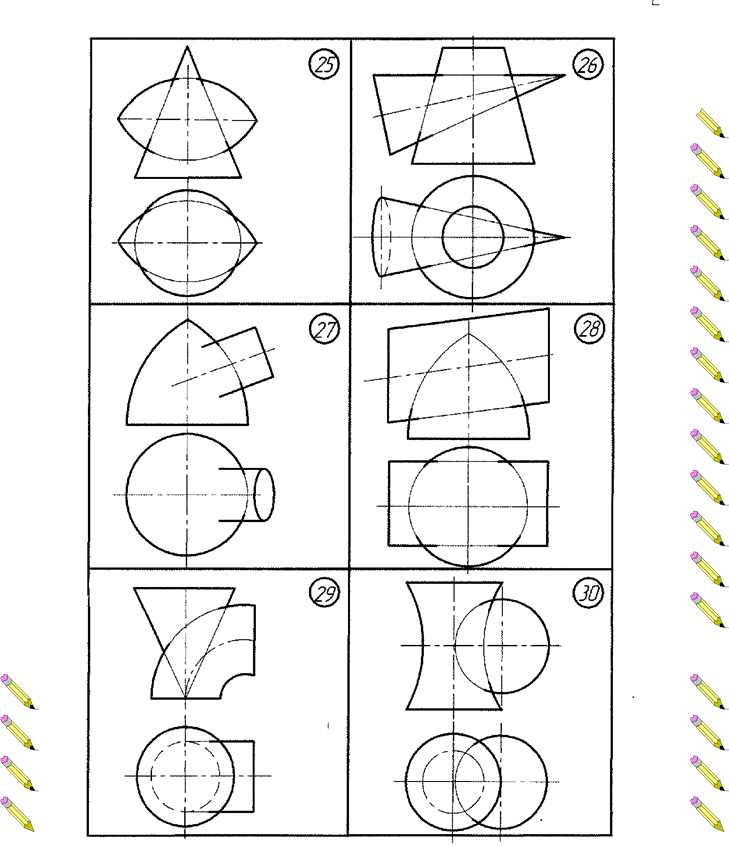
Додаток В. Варіанти до виконання завдання №3
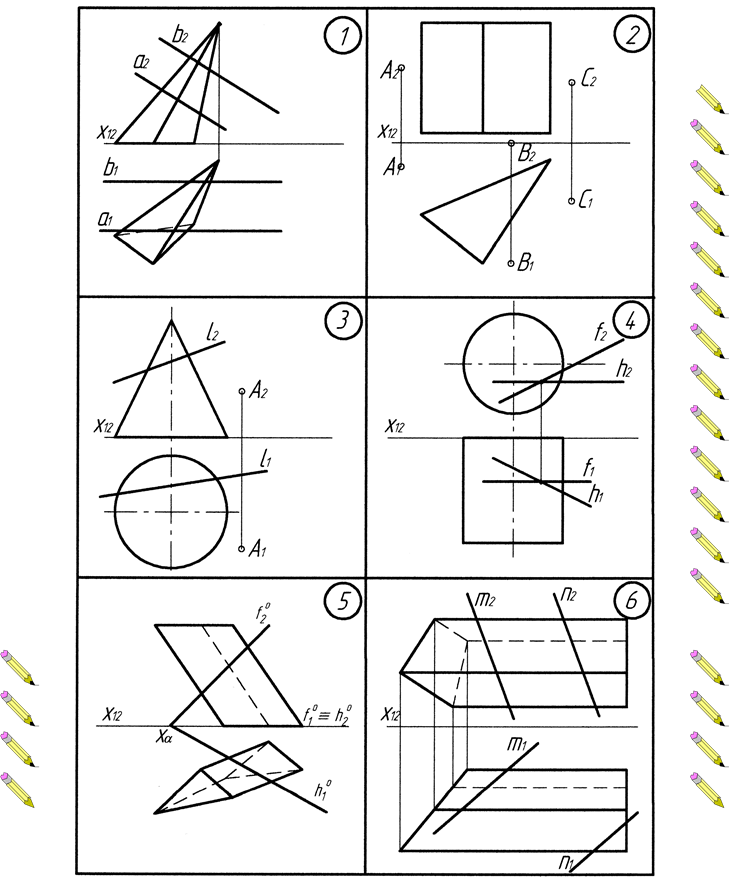
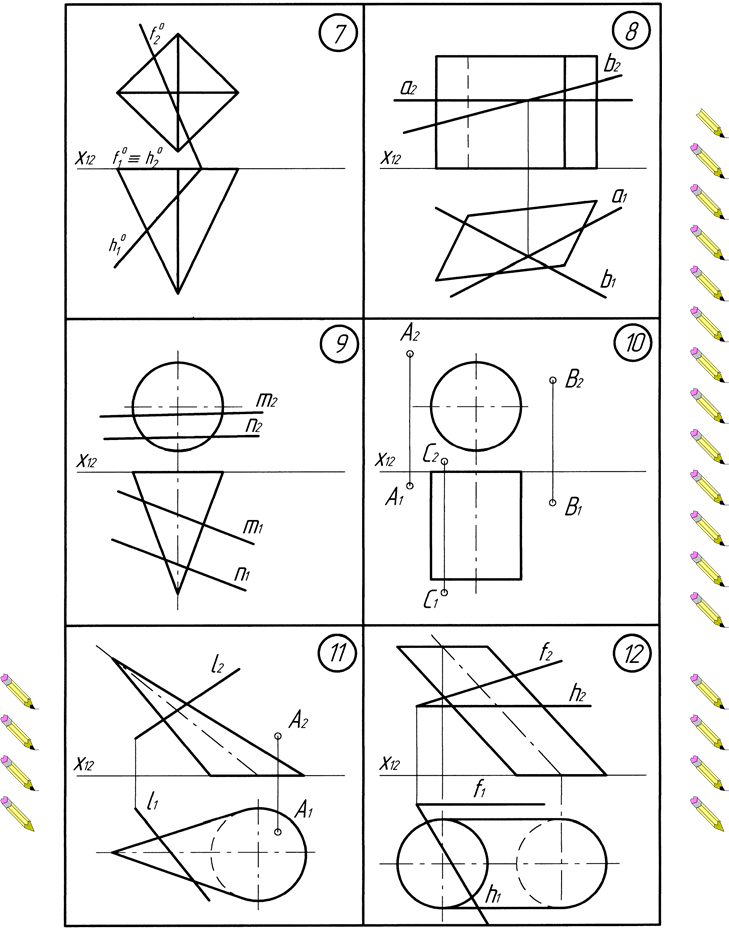
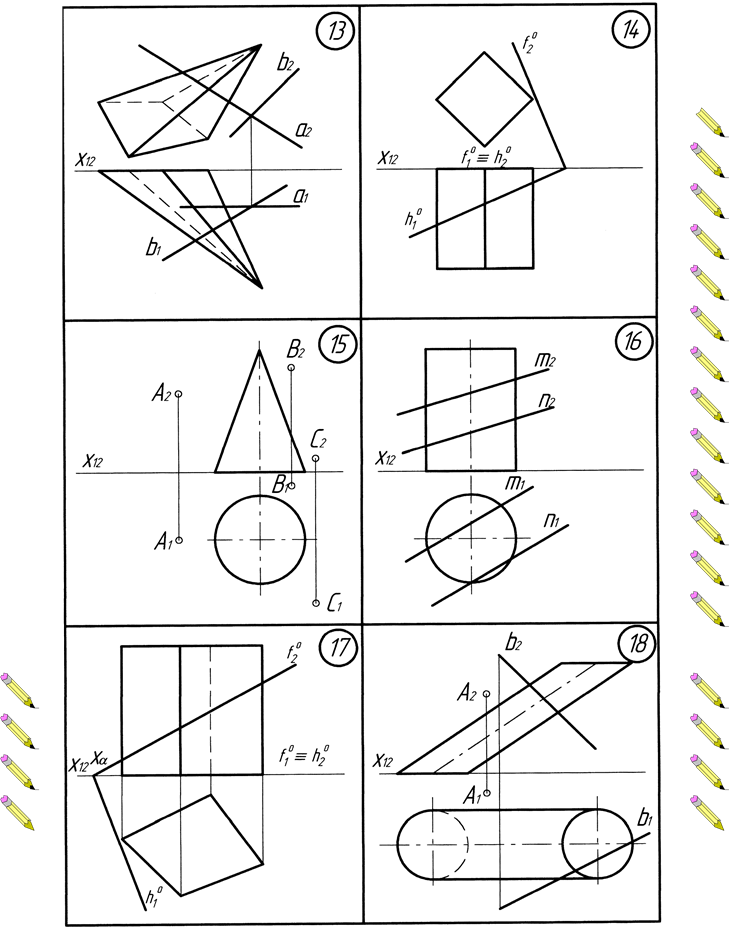
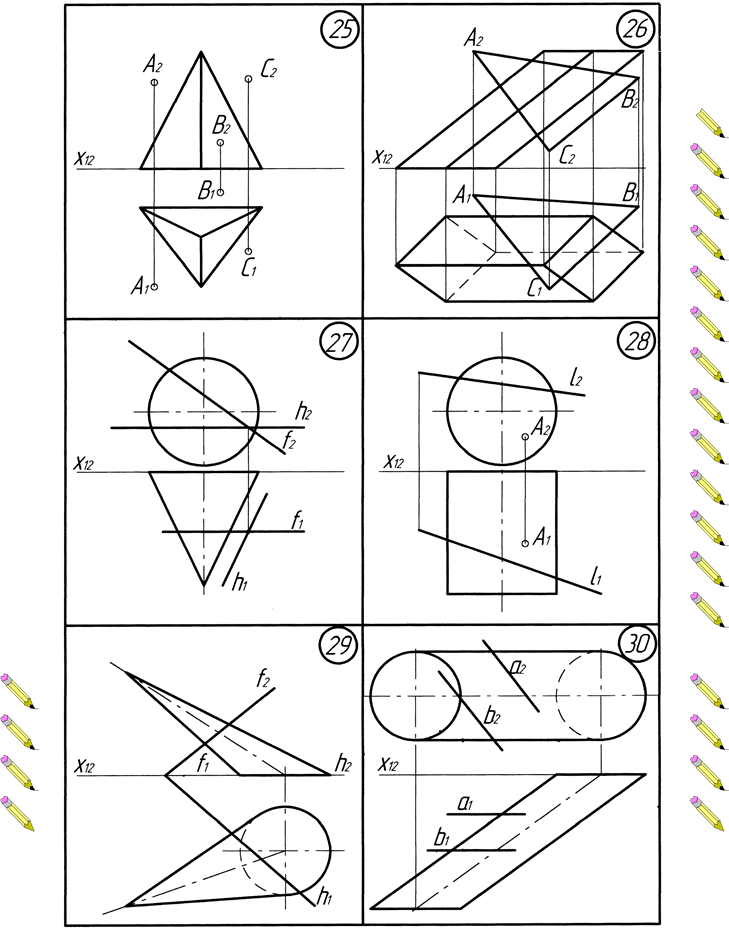
Додаток Г. Варіанти до виконання завдання №4
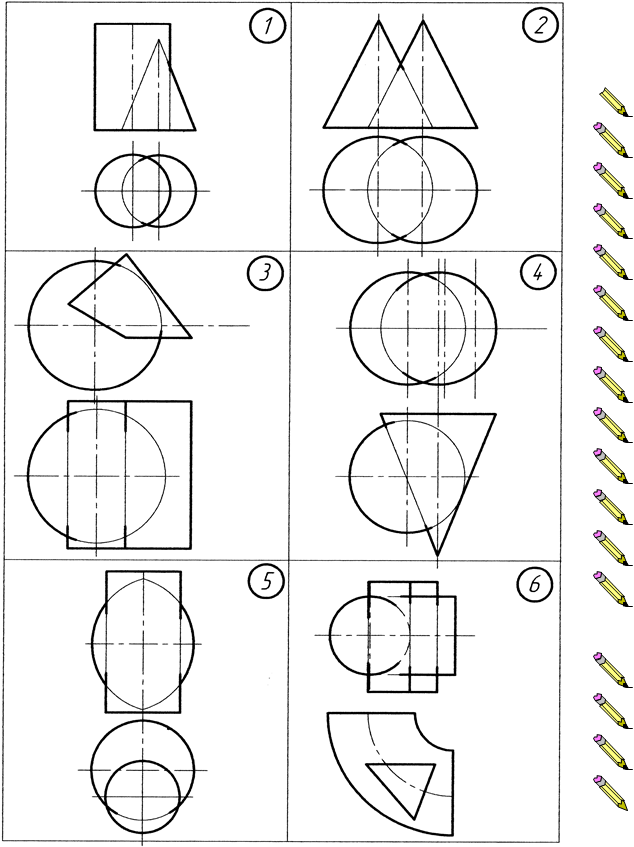
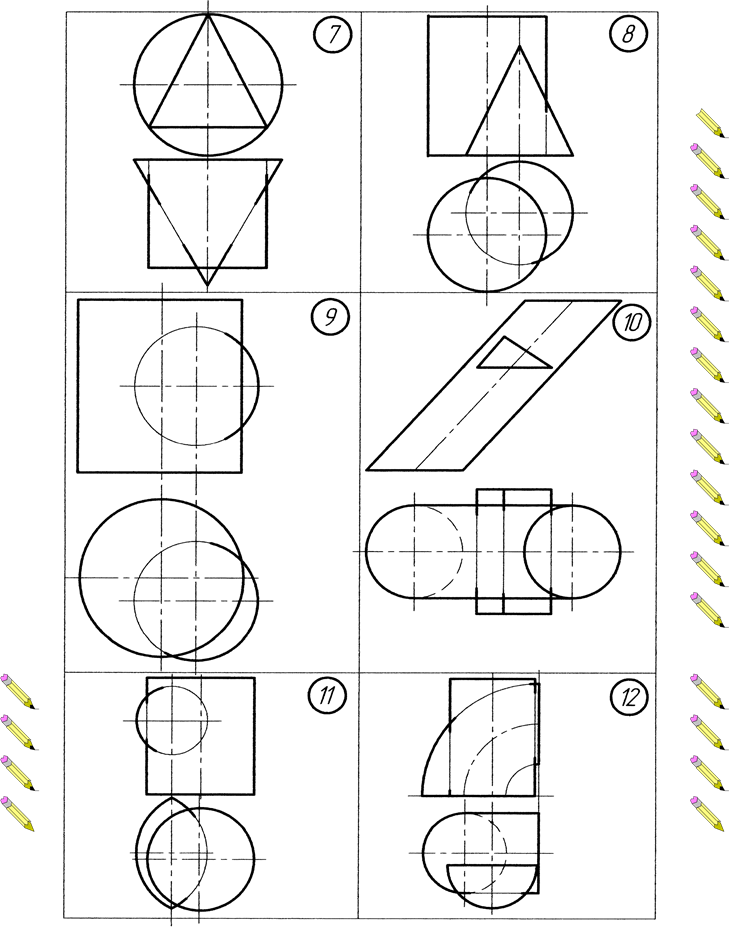
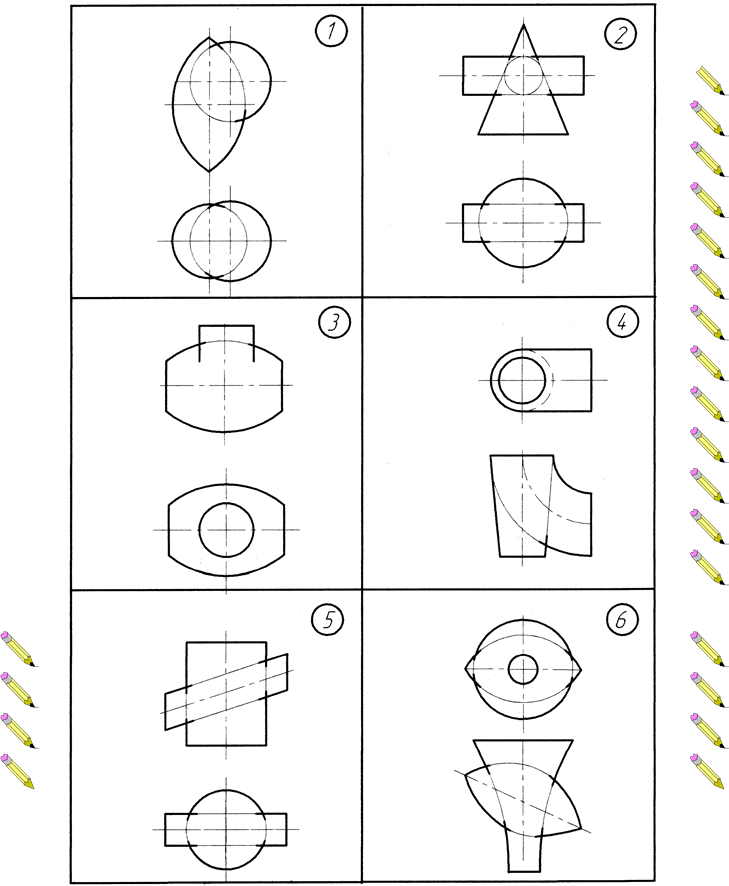
Додаток Д . Варіанти до виконання завдання №5

 НОТАТКИ
НОТАТКИ


про публікацію авторської розробки
Додати розробку