Методичні вказівки щодо проведення лабораторної роботи «Дослідження автоколивань в нелінійній автоматичній системі управління»

Дисципліна: "Основи автоматичного керування та робототехніка»

 

МЕТОДИЧНІ ВКАЗІВКИ ЩОДО ПРОВЕДЕННЯ ЛАБОРАТОРНОЇ  РОБОТИ

 

«Дослідження автоколивань  в нелінійній автоматичній системі управління»

 

 

Мета роботи: дослідження закономірностей виникнення автоколивань в нелінійній автоматичній системі управління.

 

 

Короткі теоретичні відомості

 

 

Нелінійною системою називається така система, до складу якої входить хоч би один елемент, лінеаризація якого неможлива без втрати істотних властивостей системи управління в цілому.

 У простому випадку структурна схема нелінійної автоматичної системи є послідовним з'єднанням нелінійної частини (НЧ) і лінійної частини (ЛЧ), охоплених зворотним зв'язком (див. рисунок 1).

 

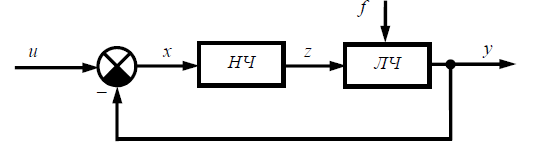
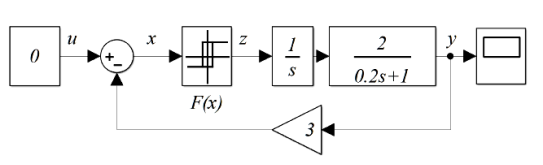
Рисунок 1 - Структурна схема нелінійної  САУ

 

 

В даному випадку вдається виділити нелінійність так, щоб вона описувалася безпосередньою залежністю між вихідною z і вхідною x величинами нелінійного елементу,  який може мати будь-яку нелінійну функцію (релейного, шматково-лінійного або криволінійного типа):

 

z = F(x) .                                                 (1)

У особливий клас нелінійних систем виділяють релейні нелінійні системи. Релейна апаратура володіє рядом переваг, завдяки яким вона широко використовується в САУ, наприклад, в програмованих логічних контролерах.

Нелінійна система в перехідному режимі може мати декілька станів стійкої або нестійкої рівноваги, тобто може знаходитися не тільки в процесі, що рівноважно сходиться, але і в стійкому сталому періодичному автоколивальному режимі.

 Стійкі власні незгасаючі коливання в нелінійній системі з певною амплітудою  А, частотою  f  і періодом  Т, що визначаються нелінійністю і внутрішніми параметрами системи, називаються автоколиваннями  (див. рисунок 2).

 

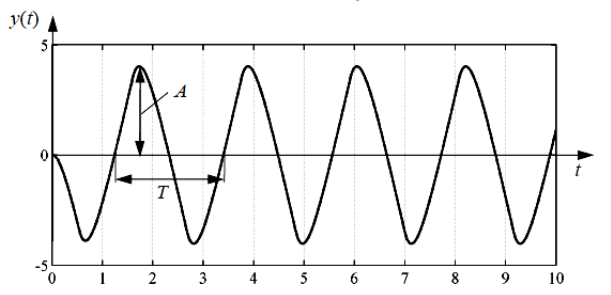
Рисунок  2 -  Перехідна характеристика стійкого автоколивального процесу

 

 

 Автоколивання  є стійким режимом, характерним тільки для нелінійних систем, тому що малі зміни параметрів системи не виводять її з цього режиму. Амплітуда і частота автоколивань  не залежить від початкових умов і рівня зовнішніх дій.

 Причиною автоколивань  часто є наявність зони нечутливості, релейної функції або гістерезису з порогом  b.

Якщо на систему подавати сигнал, частота якого може співпадати з частотою власних коливань системи, то в системі можуть виникати резонансні явища, може відбутися стрибок амплітуди.

 У загальному випадку при додатку зовнішніх періодичних дій виникає накладення власних і зовнішніх коливань.

 При збільшенні амплітуди зовнішніх дій може відбутися зрив автоколивань  власної частоти, і система переходить на частоту зовнішніх коливань. Такий режим роботи нелінійної системи називається синхронним режимом. Важлива також швидкість додатку зовнішньої дії. При стрибкоподібній дії може бути таке перерегулювання, що виводить систему в абсолютно іншу область тяжіння і з іншим режимом, в порівнянні з тим випадком, коли такаж ж по величині дія була б подана плавніше.

Розглянемо як приклад нелінійної системи автоматичну систему стабілізації напруги з нелінійним пристроєм, що керує (дтв. рисунок 3). Регульованою величиною є стабілізована напруга U_Н на опорі R_Н. Для згладжування пульсацій напруги U₀, створюваних регулюючим транзистором VT, що працює в ключовому режимі, між транзистором VT и навантаженням R_Н включений LC-фільтр з нульовим діодом D.

 

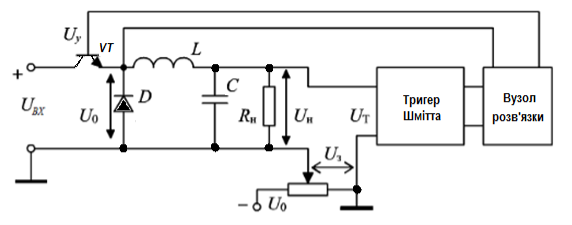
Рисунок 3 - Релейна автоматична система стабілізації напруги

 

Пристроєм, що управляє, є тригер Шмітта, що реалізований на операційному підсилювачі, статична характеристика якого має форму петлі гістерезису (див. рисунок 4, а). На вхід тригера Шмітта поступає різниця задаючої напруги U_З та регульованої величини  U_Н. Досягши різниці цих напруг порогових значень перемикання тригера U₂ та U₁ останній  змінює стан на своєму виході, перемикає регулюючий транзистор по черзі в режими відсічення і насичення. Форма вихідної напруги системи стабілізації  показана на рисунку 4, б. Розмах пульсацій ΔU вихідної напруги  визначається шириною зони гістерезису релейного елементу - тригера Шмітта.

 

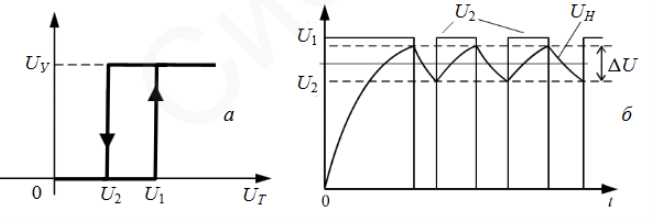
Рисунок 4 - Характеристики системи стабілізації напруги

 

 

Порядок виконання роботи

 

 

Складіть на робочому полі програми SamSim  схему моделі для дослідження автоколивань  в нелінійній системі автоматичного управління  (див. рисунок 5), що складається з нелінійної частини (ланка з нелінійною характеристикою - двопозиційне реле з гістерезисом) і лінійної частини (інтегруюча ланка і інерційна ланка 1-го порядку).

 

 

 

 

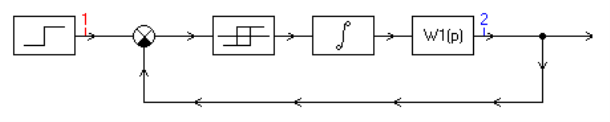
Рисунок  5 -  Схема моделі для дослідження автоколивань в нелінійній системі

 

 

Задайте для ланок нелінійної системи чисельні значення параметрів згідно таблиці варіантів  (див. таблицю 1),

 

Таблиця 1 - Значення параметрів ланок нелінійної САУ

Ланка		Варіанти
		1	2	3	4	5	6	7
Двохпозиційне реле з гістерезисом	В	1,0	1,1	0,8	0,5	0,6	0,7	0,9
	b	0,3	0,35	0,2	0,2	0,2	0,25	0,15
	k=B/b
	q(A)
Інтегруюча ланка	k1	1	1	1	1	1	1	1
	Т1	0,8	0,9	0,7	0,6	0,5	0,4	0,85
Інерційна ланка 1-го порядку	k2	1,3	1,2	1,4	2,1	2,2	1,0	1,6
	T2	0,3	0,2	0,1	0,25	0,3	0,15	0,35

 

Подавши на вхід схеми одиничний ступінчастий сигнал, одержіть перехідну характеристику вихідного сигналу (див. приклад на рисунку  6).

 

 

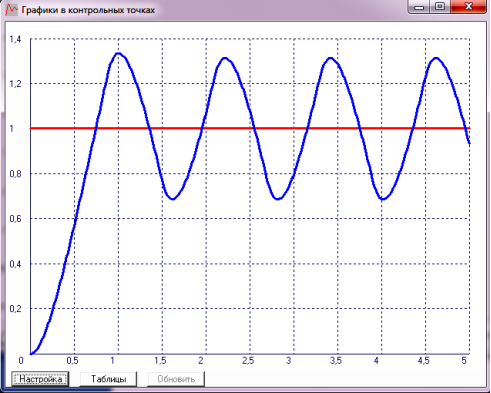
Рисунок  6 – Перехідна характеристика нелінійної системи при дії  одиничного ступінчастого сигналу

 

 

По перехідній характеристиці визначите амплітуду А і  період T симетричних автоколивань сталого періодичного режиму (дів. рисунки 2, 6). Обчисліть частоту автоколивань  f.

 Результати вимірювань і розрахунків занесіть в таблицю 2.

 

Таблиця 2 - Результати вимірювань і розрахунків

Параметр	Розрахунок в програмі SamSim	Алгебраїчний  розрахунок
Амплітуда  А
Період  T, с
Частота f, Гц

 

Збільшить амплітуду ступінчастого вхідного сигналу в два рази. Визначте амплітуду А і  період T автоколивань. Переконайтеся, що амплітуда і частота автоколивань в нелінійних системах не залежить від рівня зовнішньої дії, а викликані тільки властивостями самої системи.

Встановіть на вході схеми джерело лінійно зростаючої напруги і  одержіть перехідну характеристику вихідного сигналу  (див. приклад на рисунку 7). Переконайтеся, що лінійна зовнішня дія не змінює амплітуду і частоту автоколивань.

 

 

 

 

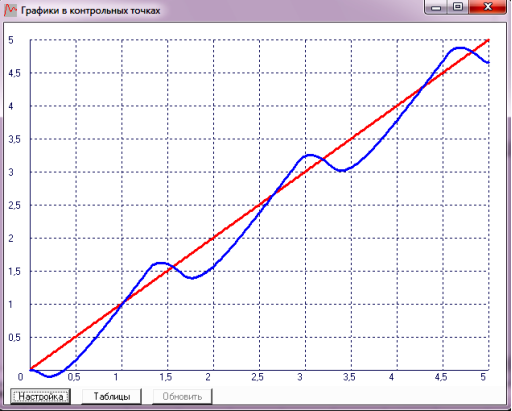
Рисунок  7 – Перехідна характеристика нелінійної САУ при лінійній дії

 

 

Виконайте розрахунок параметрів симетричних автоколивань  алгебраїчним методом на основі гармонійної лінеаризації нелінійності.

 Суть гармонійної лінеаризації полягає в опису нелінійної ланки лінійним рівнянням, яке виходить при зневазі вищими гармоніками в розкладанні нелінійної функції в ряд Фур'є. В цьому випадку  нелінійний елемент можна замінити лінійною ланкою, параметри якої визначаються при гармонійній вхідній дії з умови рівності амплітуд перших гармонік на виході нелінійного елементу і еквівалентної йому лінійної ланки.

  Розрахуйте  максимальну частоту автоколивань нелінійної системі за формулою

 

.                                                (2)

 

Результат розрахунку частоти  автоколивань   f_макс  занесіть в таблицю 2.

 

Амплітуда автоколивань   А для заданої системи визначається розрахунковим шляхом за формулою (3) розрахунку коефіцієнта гармонійної лінеаризації нелінійного елементу «Двопозиційне реле з гістерезисом»  (див. рисунок  8).

 

 

 

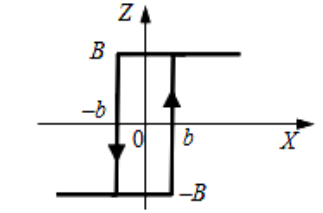
Рисунок 8 – Зовнішній вигляд шматково-лінійної релейної нелінійності

 

 

  ,                                                 (3)

 

де  q(A) - коефіцієнт гармонійної лінеаризації;

      B, b - статичні характеристики нелінійності реле;

А - амплітуда автоколивань.

 

Коефіцієнт гармонійної лінеаризації q(A) визначається по заданих параметрах САУ за формулою

 

 

.                                              (4)

 

де k = B/b.                                                                                                                    (5)

 

З формули (3) виходить розрахунок максимальної амплітуди автоколивань

 

 

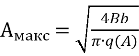.                                                 (6)

 

Результат розрахунку параметра А занесіть в таблицю  2.

Порівняйте результати комп'ютерного моделювання САУ і алгебраїчного розрахунку на основі гармонійної лінеаризації нелінійності.

 

 

 

 

 

 

 

 

Зміст звіту з роботи

 

 1. Назва і мета роботи.

 2. Схема досліджуваної моделі в програмному середовищі SamSim.

 3. Перехідна характеристика нелінійної системи.

 4. Таблиці розрахунків і вимірювань

 5. Розрахункові формули.

   6. Висновок по роботі і короткі відповіді на контрольні питання.

 

 

Контрольні питання

 

1. Яка система називається нелінійною?

2. У якому випадку можливо виникнення автоколивань в нелінійній системі?

3. Приведіть приклади нелінійностей в реальних технічних пристроях.

 

 

Література

 

1.               Головінський Б.Л. Теорія автоматичного управління / Б.Л. Головінський, Ю.В. Шуруб, В.П. Лисенко. - К.: ВЦ НУБіП України, 2012.
2.               Климентовський Ю.А. Технiчнi засоби автоматики / Ю.А. Климентовський, А.М. Гладкий. – К.: Видавництво «КВIЦ», 2003.
3.               Попович М.Г. Теорія автоматичного керування: підруч. для студ. вищ. техн. навч. закл. / М.Г. Попович, О.В. Ковальчук. – К.: Либідь, 2007.