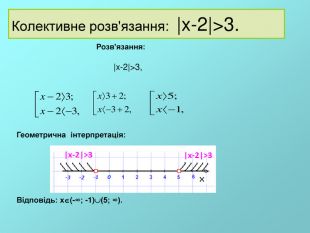
Презентація до уроку з алгебри в 9 класі "Нерівності,що містять змінну під знаком модуля"
Про матеріал
Презентація до уроку з алгебри в 9 класі "Нерівності,що містять змінну під знаком модуля----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
ДЯКУЮ !
ppt
До підручника
Алгебра (підручник для класів із поглибленим вивченням математики) 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


















![Приклади: |х|< 2, -2<х<2, (-2;2). -4 х 4, або [-4;4]. -2 2 х -4 4 |х| 4 х Приклади: |х|< 2, -2<х<2, (-2;2). -4 х 4, або [-4;4]. -2 2 х -4 4 |х| 4 х](/uploads/files/23459/28369/28300_images/20.jpg)



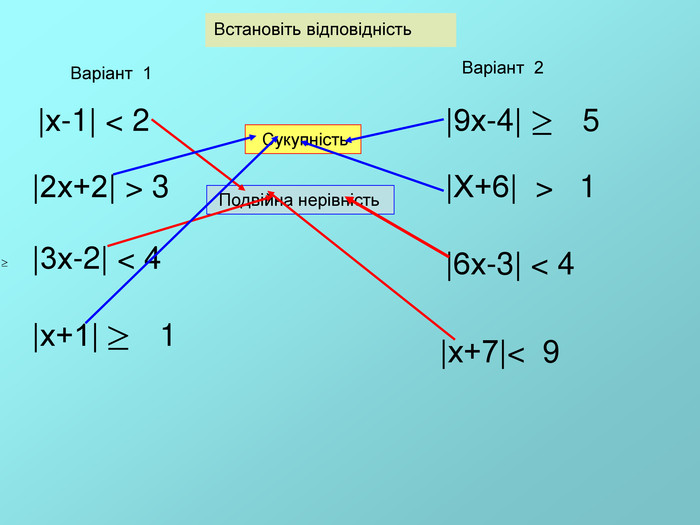
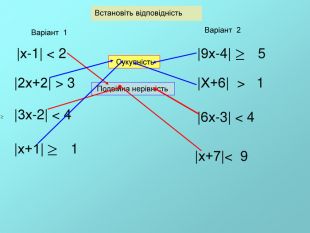
![Розв'яжіть усно |х| > 1, Відповідь:(- ;-1) (1; ) |х| 5, -1 1 х 5 -5 х Відповідь: ( - ;-5] [5; ) Розв'яжіть усно |х| > 1, Відповідь:(- ;-1) (1; ) |х| 5, -1 1 х 5 -5 х Відповідь: ( - ;-5] [5; )](/uploads/files/23459/28369/28300_images/25.jpg)


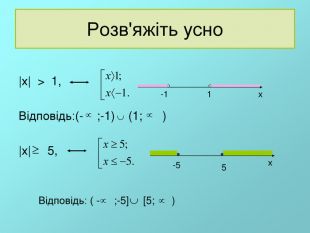
![Тести Розв'язати нерівності: Варіант 1 Варіант 2 1. |х-6| < 4. 1.|х-8| < 6. А)(2;-10); Б)(-2;10); В)(2;10); Г)[2;10). В) А)(-2;-14); Б)(2;14); В)[2;14); Г)[2;1]. Б) 2. |х-1| 2. 2. |х-3| 1. А)(-∞; -1][3; ∞); Б) (-∞; -1)(3; ∞); В)(-∞; -1](3; ∞); Г) (-∞; -1)[3; ∞); А) А)(-∞; -2](4; ∞); Б) (-∞; 2)(4; ∞); В)(∞; 2][4; ∞); Г) (-∞; 2)[4; ∞); В) Розв'язати нерівності: Тести Розв'язати нерівності: Варіант 1 Варіант 2 1. |х-6| < 4. 1.|х-8| < 6. А)(2;-10); Б)(-2;10); В)(2;10); Г)[2;10). В) А)(-2;-14); Б)(2;14); В)[2;14); Г)[2;1]. Б) 2. |х-1| 2. 2. |х-3| 1. А)(-∞; -1][3; ∞); Б) (-∞; -1)(3; ∞); В)(-∞; -1](3; ∞); Г) (-∞; -1)[3; ∞); А) А)(-∞; -2](4; ∞); Б) (-∞; 2)(4; ∞); В)(∞; 2][4; ∞); Г) (-∞; 2)[4; ∞); В) Розв'язати нерівності:](/uploads/files/23459/28369/28300_images/29.jpg)