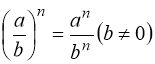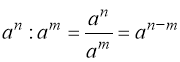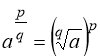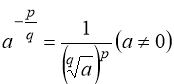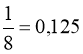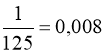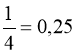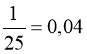Методичний посібник "Показникові рівняння"
Управління освіти
Прилуцької міської ради
Чернігівської області
Чигріна Г.М.
ПОКАЗНИКОВІ РІВНЯННЯ

Прилуки
2010
Чигріна Г.М. Показникові рівняння.
Методичний посібник. Прилуки: Гімназія № 1, 2010.
Рецензенти : 1) доцент кафедри природничо-математичних дисциплін та інформаційних технологій ЧОІППО ім. К.Д.Ушинського, кандидат педагогічних наук Грамбовська Лариса Володимирівна;
2) методист відділу природничо-математичних дисциплін ЧОІППО ім. К.Д.Ушинського Хандога Раїса Миколаївна.
У даному посібнику висвітлено короткі теоретичні відомості, основні типи показникових рівнянь, методи їх розв’язування, наведено приклади розв’язування типових завдань. Подано вправи для самостійної роботи та варіанти індивідуальних завдань.
Пропонований матеріал може бути використаний як на уроках, так і в позакласній роботі.
Посібник може бути використаний у школах (класах) з поглибленим вивченням математики, у ліцеях та гімназіях природничо-математичного профілю та для самостійної підготовки учнів до складання ЗНО та ДПА.
Погоджено на засіданні методичної ради міського НМЦ управління освіти Прилуцької міської ради,
протокол № 2 від 24. 11. 2010 р.
Рекомендовано до друку міським НМЦ.
Зміст
Передмова ………………………………………………. ……………4
І. Степінь з натуральним, цілим та дробовим показником……………5
1.1 Степінь з натуральним показником………………………………5
1.2 Степінь з цілим показником………………………………………5
1.3 Степінь з дробовим (раціональним) показником…………….....7
1.4 Показникова функція……………………………………………...7
1.5 Перетворення показникових виразів……………………………..8
ІІ. Розв’язування показникових рівнянь……………………………....12
2.1 Загальні відомості……………………………..............................12
2.2 Рівняння виду ![]() ………………………………………..14
………………………………………..14
2.3 Рівняння виду ![]() ………………………………………….18
………………………………………….18
2.4 Рівняння виду ![]() ………………………………………...19
………………………………………...19
2.5 Рівняння виду ![]() ………………………………………..21
………………………………………..21
2.6 Рівняння виду ![]() …………………………………………22
…………………………………………22
2.7 Рівняння виду ![]() …
… ![]() ……………………..23
……………………..23
2.8 Рівняння виду ![]()
![]() 25
25
2.9 Рівняння виду ![]() …………………………28
…………………………28
2.10 Рівняння виду ![]() …………………………..32
…………………………..32
2.11 Рівняння виду ![]() ……………………36
……………………36
2.12 Використання властивостей монотонності функції при розв’язанні показникових рівнянь…………………………………….42
ІІІ. Розв’язування степенево-показникових рівнянь…………………47
ІV. Розв’язування показникових рівнянь (за збірником ДПА)………52
V. Варіанти індивідуальних завдань …………………………………64
VІ. Вправи для самостійної роботи …………………………………..66
Відповіді та вказівки …………………………………………………..70
Література……………………………………………………………….75
Передмова
Мета навчання математики в класах математичного та фізико-математичного профілів полягає у забезпеченні загальноосвітньої підготовки з математики, необхідної для успішної самореалізації особистості у динамічному соціальному середовищі, її соціалізації, і достатньої для успішного вивчення фізики та інших, в першу чергу, природничих предметів, продовження навчання у вищих закладах освіти за спеціальностями, або безпосередньо пов’язаними з математикою, або за спеціальностями, де вона відіграє роль апарату для вивчення й аналізу закономірностей реальних явищ і процесів.
Посібник вміщує показникові рівняння, більшість з яких пропонувалися на вступних іспитах з математики до НТУУ «КПІ». У навчальному посібнику розглянуто тотожні перетворення показникових виразів, обчислення їх значень, основні методи розв’язування показникових рівнянь, задачі з параметрами.
У посібнику містяться короткі теоретичні відомості, основні типи показникових рівнянь, методи їх розв’язування, приклади розв’язування типових завдань та завдань, що пропонуються на ДПА, вправи для самостійної роботи, до яких у кінці додаються відповіді, та варіанти індивідуальних завдань. Кожне з індивідуальних завдань містить десять однотипних задач. Їх виконання учнями сприятиме активізації самостійної роботи та виробленню навичок оформлення письмової роботи.
Посібник може бути використаний при організації самостійної індивідуальної роботи в школах (класах) з поглибленим та вивченням математики, у ліцеях та гімназіях природничо-математичного профілю та для самостійної підготовки учнів до складання ЗНО та ДПА.
І. Степінь з натуральним, цілим і дробовим показником
1.1. Степінь з натуральним показником
1.1.1. Степенем ![]() числа а (
числа а (![]() ,
, ![]() ) з натуральним показником
) з натуральним показником ![]() називається добуток п співмножників, кожен з яких дорівнює а, тобто
називається добуток п співмножників, кожен з яких дорівнює а, тобто
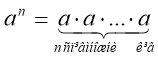 , (1)
, (1)
де ![]() - степінь числа; а – основа степеня; п – показник степеня.
- степінь числа; а – основа степеня; п – показник степеня.
1.1.2. Піднесення до степеня – знаходження значення степеня.
1.1.3. Основна властивість степеня:
![]() . (2)
. (2)
1.2. Степінь з цілим показником
1.2.1. Степенем ![]() числа а (
числа а (![]() ,
, ![]() ) з цілим показником п називається число, обумовлене наступним чином:
) з цілим показником п називається число, обумовлене наступним чином:
1) ![]() , якщо
, якщо ![]() ; (3)
; (3)
2) 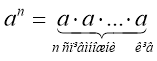 , якщо
, якщо ![]() ; (4)
; (4)
3) 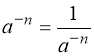 , якщо
, якщо ![]() ,
, ![]() , (5).
, (5).
Примітка. Степінь числа 0 може мати тільки додатний показник (0п = 0 при п > 0). Вираз 00 і 0n при п < 0 на множині дійсних чисел не має змісту.
1.2.2. Правила знаків при піднесенні до додатного (2п) та від’ємного (2п + 1) степеня числа а (а > 0):
1) ![]() ; (6)
; (6)
2) ![]() . (7)
. (7)
Зокрема, ![]() ;
; ![]() .
.
Приклади:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
1.2.3. Основні властивості степеня з цілими показниками, які виражають правила дій зі степенями, наведені в табл. 1.1.
Таблиця 1.1.
|
|
Дія |
Правило |
|
1 |
Нульовий степінь |
|
|
2 |
Перший степінь |
|
|
3 |
Від’ємний степінь |
|
|
4 |
Множення степенів з однаковими основами |
|
|
5 |
Степінь добутку (множення степенів з однаковими показниками) |
|
|
6 |
Степінь частки (дробу) (ділення степенів з однаковими показниками) |
|
|
7 |
Ділення степенів з однаковими основами |
|
|
8 |
Піднесення степеня до степеня |
|
|
9 |
Степінь з додатнім дробовим показником |
|
|
10 |
Степінь з від’ємним дробовим показником |
|
|
11 |
Степінь під модульного виразу |
|
Примітка. У дужках дані дії, відповідні читанню формул справа наліво.
1.3. Степінь з дробовим (раціональним показником)
1.3.1. Степенем ![]() числа а (
числа а (![]() ;
;![]() ;
; ![]() ) з раціональним показником п називається число, обумовлене наступним чином:
) з раціональним показником п називається число, обумовлене наступним чином:
1) якщо ![]() , то
, то ![]() є степенем з цілим показником і визначається у відповідності з п. 1.2.1.;
є степенем з цілим показником і визначається у відповідності з п. 1.2.1.;
2) якщо п – раціональне число ( , де p – ціле число;
, де p – ціле число; ![]() - натуральне число), то
- натуральне число), то
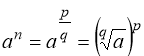 . (8)
. (8)
Примітка. 1. Якщо ![]() і
і ![]() то:
то: ![]() .
.
2. Якщо 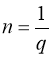 (
(![]() ;
;![]() ), то:
), то: 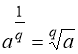 .
.
3.Для від’ємних основ раціональний показник степеня не розглядається.
1.3.2. Степінь ![]() з раціональним показником має всі властивості степеня з цілими показниками, наведеними в табл. 1.1. та п. 1.2.
з раціональним показником має всі властивості степеня з цілими показниками, наведеними в табл. 1.1. та п. 1.2.
1.4. Показникова функція
Показниковою називається функція, задана формулою ![]() , де а – деяке додатне число, не рівне одиниці.
, де а – деяке додатне число, не рівне одиниці.
Основні властивості показникової функції:
- область визначення функції – множина R усіх дійсних чисел;
- область значень аргументу х – множина R+ усіх додатних дійсних чисел;
-
функція
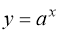 при
при 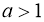 - монотонно зростаюча (рис. 1.1.);
- монотонно зростаюча (рис. 1.1.);
-
функція
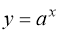 при
при 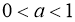 - монотонно спадна (рис. 1.2.).
- монотонно спадна (рис. 1.2.).
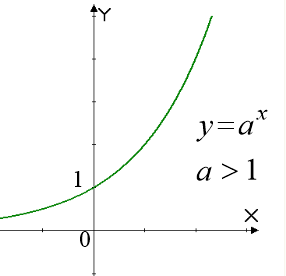
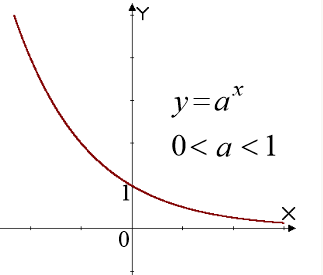
Рис. 1.1 Рис. 1.2.
Перелічимо основні властивості степеня ![]() з цілим показником, що ґрунтуються на монотонності показникової (
з цілим показником, що ґрунтуються на монотонності показникової (![]() ) функції:
) функції:
1) якщо ![]() , то:
, то: ![]() ;
;
2) якщо ![]() , то:
, то: ![]() ;
;
3) якщо ![]() і
і ![]() , то
, то ![]() ;
;
4) якщо ![]() і
і ![]() , то
, то ![]() ;
;
5) якщо ![]() , то:
, то: ![]() ;
;
6) якщо ![]() і
і ![]() , то:
, то: ![]() ;
;
7) якщо ![]() і
і ![]() , то:
, то: ![]() ;
;
8) якщо ![]() і
і ![]() , то:
, то: ![]() ;
;
9) якщо ![]() і
і ![]() , то: для довільного
, то: для довільного ![]() існує єдине число п, таке, що
існує єдине число п, таке, що ![]() .
.
1.5. Перетворення показникових виразів
1.5.1. Корисно знати деякі «стандартні» для показникових рівнянь перетворення основ:
1) 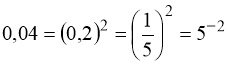 ;
;
2) 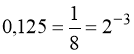 ;
;
3)  ;
;
4) 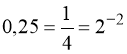 ;
;
5) 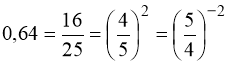 ;
;
6) 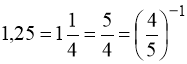 ;
;
7) 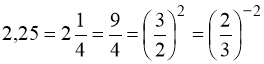 ;
;
8) 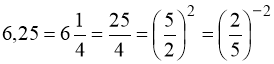 .
.
1.5.2. Найбільш часто зустрічаються степені чисел 2, 3, 5, 7, і варіанти їх записів наведені в табл. 1.2.
Таблиця 1.2.
|
Показник степеня |
Основа |
|||
|
2 |
3 |
5 |
7 |
|
|
- 3 |
|
|
|
|
|
- 2 |
|
|
|
|
|
- 1 |
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
|
1 |
2 |
3 |
5 |
7 |
|
2 |
4 |
9 |
25 |
49 |
|
3 |
8 |
27 |
125 |
343 |
|
4 |
16 |
81 |
625 |
2401 |
|
5 |
32 |
243 |
3125 |
16807 |
|
6 |
64 |
729 |
15625 |
117649 |
Приклад 1. Спростити вираз:
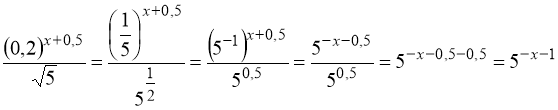 ;
;
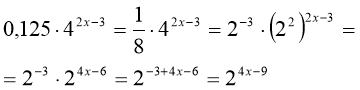
Приклад 2. Обчислити:
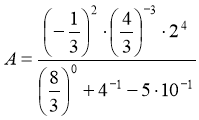 .
.
Маємо: 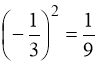 ;
; 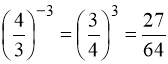 ;
;
Тому: 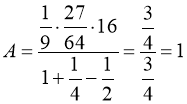 .
.
1.5.3. Інколи в якості основи використовують нескінченний десятковий дріб (наприклад: 0,(3) = 0,333 …), який у процесі розв’язання рівняння потребує перетворення у звичайний. Нагадаємо правила перетворення.
Правило 1. Щоб перетворити чистий нескінчений періодичний десятковий дріб у звичайний, беруть його період чисельником, а в знаменнику пишуть цифру 9 стільки разів, скільки цифр у періоді.
Приклад 3. Нескінчений періодичний дріб перетворити у звичайний.
1) 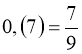 ;
;
2) 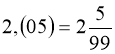 ;
;
3) 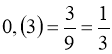 .
.
Правило 2. Щоб перетворити змішаний нескінченний періодичний десятковий дріб у звичайний, віднімають від числа, що стоїть до другого періоду, число, що стоїть до першого періоду, і отриману різницю записують у чисельник, а в знаменник пишуть цифру 9 стільки разів, скільки цифр в періоді, зі стількома нулями на кінці, скільки цифр між комою і першим періодом.
Приклад 4. Нескінченний періодичний дріб перетворити у звичайний:
1) 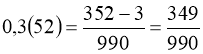 ;
;
2) 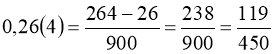 ;
;
3) 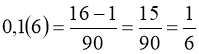 .
.
1.5.4. Один із найбільш розповсюджених методів перетворення показникових рівнянь – винесення за дужки спільного множника.
Приклад 5. Спростити:
1) ![]() .
.
2) ![]() .
.
Скористаємося перетвореннями:
![]() ;
; ![]() .
.
Тоді: ![]() .
.
Винесемо за дужки степінь з найменшим показником ![]() . Для цього перетворимо:
. Для цього перетворимо: ![]() .
.
Тому:
![]()
3) ![]() .
.
Перетворимо: ![]() .
.
![]() ;
;
![]() .
.
Тому:
![]() .
.
4)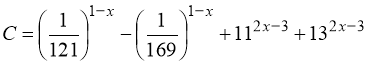 .
.
Перетворимо:
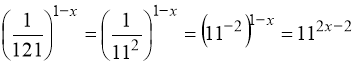 .
.
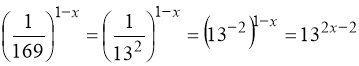 .
.
Тому:
![]()
![]()
![]()
![]()
![]() .
.
ІІ. Розв’язування показникових рівнянь
2.1. Загальні відомості
Показникове рівняння містить змінну під знаком показникової функції.
Найпростішим показниковим рівнянням називають рівняння виду ах = b, де a >0 , a ![]() 1.
1.
Це трансцендентні, тобто неалгебраїчні, рівняння. Тільки окремі з них можна звести до алгебраїчних рівнянь методом логарифмування, зведення до спільної основи, групування доданків, заміни змінної тощо. Загального методу розв’язування показникових рівнянь не існує. Окремі методи розв’язування розглянутих у шкільному курсі математики показникових рівнянь ґрунтуються на властивостях показникової функції і формулах перетворень показникових виразів. Найбільш частіше використовують дві наступні теореми:
ТЕОРЕМА 1. Якщо основа а (а > 0 і а ≠ 1) двох степенів і самі степені рівні, то показники степенів також рівні:
![]() при а > 0 , а ≠ 1.
при а > 0 , а ≠ 1.
ТЕОРЕМА 2. Якщо для рівних степенів показники степеня рівні і відмінні від нуля, то рівні і основи степенів:
![]() при а > 0; b > 0; f (х) ≠ 0. (10)
при а > 0; b > 0; f (х) ≠ 0. (10)
Основна складність при розв’язуванні показникових рівнянь полягає в перетворенні даного рівняння до виду, коли вдається застосувати теорему 1 або 2.
Основні методи розв’язання показникових рівнянь:
1) зведення обох частин рівняння до однієї основи -
цим методом розв’язуються, наприклад, рівняння виду ![]() ,
, ![]() , коли основи а і b можна звести до однієї, додатної і відмінної від одиниці основи;
, коли основи а і b можна звести до однієї, додатної і відмінної від одиниці основи;
2) зведення обох частин рівняння до одного показника -
цим методом розв’язуються, наприклад, рівняння виду ![]() , коли основи а і b не зводяться до однієї додатної або відмінної від одиниці основи;
, коли основи а і b не зводяться до однієї додатної або відмінної від одиниці основи;
3) логарифмування обох частин рівняння -
цим методом розв’язуються, наприклад, рівняння виду ![]() , при будь-яких, додатних і відмінних від одиниці основах а і b;
, при будь-яких, додатних і відмінних від одиниці основах а і b;
4) винесення спільного множника за дужки -
цим методом розв’язуються рівняння, ліва частина яких є сумою одночленів виду ![]() , а права – числом;
, а права – числом;
5) введення додаткової змінної (метод заміни) -
це найбільш розповсюджений метод розв’язування показникових рівнянь, розглянутий в п. 2.9, 2.10, 2.11;
6) використання властивостей монотонності функції -
цей метод детально розглянутий в п. 2.12.
7) графічний спосіб -
цей метод полягає в перетворенні рівняння до такого виду, щоб ліва і права частини рівняння були функції, графіки яких можна побудувати. Абсциси точок перетину графіків цих функцій є розв’язком даного рівняння. Графічний спосіб розв’язування показникових рівнянь у даній роботі не розглядається.
Іще раз відмітимо, що всі ці способи є штучними, породженими штучністю всіх розглянутих у шкільному курсі математики показникових рівнянь. Проте навчальний ефект розв’язання показникових рівнянь і їх надзвичайна поширеність у завданнях ДПА та ЗНО дозволяє сподіватися на користь цієї методичної розробки.
2.2. Рівняння виду
![]() , (9)
, (9)
де а ![]() R, а > 0, а ≠ 1, f = f(х), φ = φ(х) – деякі функції, розв’язуються з використанням теореми 1 і зводяться до розв’язування рівняння виду f(х)= φ(х). Основна складність полягає, як правило, у перетворенні даного рівняння до рівняння виду (9).
R, а > 0, а ≠ 1, f = f(х), φ = φ(х) – деякі функції, розв’язуються з використанням теореми 1 і зводяться до розв’язування рівняння виду f(х)= φ(х). Основна складність полягає, як правило, у перетворенні даного рівняння до рівняння виду (9).
Приклад 6.
Розв’язати рівняння 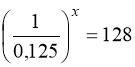 . (10)
. (10)
Розв’язання. Перетворимо: 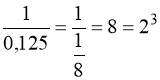 ; 128 = 27.
; 128 = 27.
Тому: 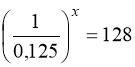
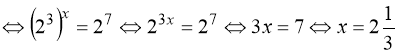 .
.
Приклад 7.
Розв’язати рівняння ![]() . (11)
. (11)
Розв’язання. Перетворимо: 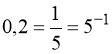 .
.
Тому:![]()
![]()
![]() або х = 2.
або х = 2.
Приклад 8.
Розв’язати рівняння ![]() . (12)
. (12)
Розв’язання. Перетворимо: ![]() ; 144 = 122.
; 144 = 122.
Тому:
![]()
![]() .
.
Приклад 9.
Розв’язати рівняння 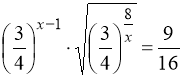 . (13)
. (13)
Розв’язання.
Перетворимо: 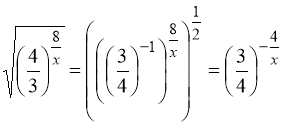 ;
; ![]()
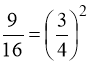 .
.
Тому: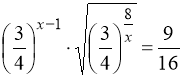
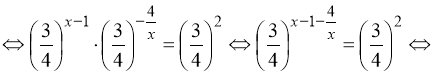
 або х = 4.
або х = 4.
Приклад 10.
Розв’язати рівняння ![]() . (14)
. (14)
Розв’язання. Перетворимо нескінченний періодичний десятковий дріб 0,1(6) у звичайний: 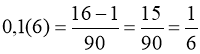 ;
; 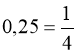 .
.
Тому: ![]()
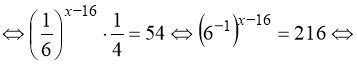
![]() .
.
Приклад 11.
Розв’язати рівняння ![]() . (15)
. (15)
Розв’язання. Зовні складне рівняння (15) може бути досить просто зведене до рівняння виду (9) шляхом відповідного групування одночленів і винесення за дужки спільного множника.
Перетворимо: 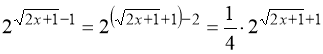 ;
; 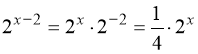 .
.
Тому:![]()
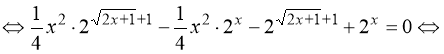
![]()
![]()
![]() . (16)
. (16)
Рівняння (16) рівносильне сукупності двох рівнянь:
1) ![]() або х = – 2;
або х = – 2;
2) ![]()
![]()
![]() або х = 4.
або х = 4.
Корені х = – 2 і х = 0 – сторонні, так як не задовольняють рівняння (15).
Відповідь: ![]()
Приклад 12.
Розв’язати рівняння ![]() . (17)
. (17)
Розв’язання.
Перетворимо: 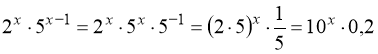 .
.
Тому:
![]()
![]() .
.
Наведемо з короткими коментарями декілька перетворень показникових рівнянь до рівняння виду (9):
1) 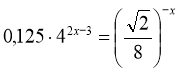 . (18)
. (18)
Перетворимо: 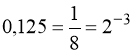 ;
;
![]() ;
;
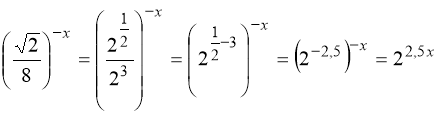 .
.
Тому: 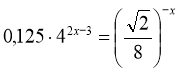
![]() .
.
2) ![]() . (19)
. (19)
Помічаємо, що 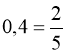 ;
; 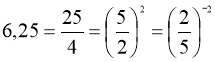 .
.
Тому: ![]()
![]()
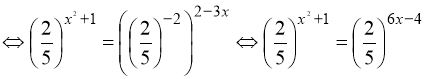 .
.
3) 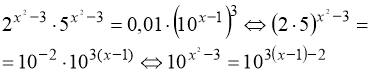
4) 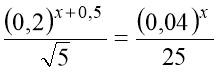 . (20)
. (20)
Помічаємо, що: 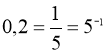 ;
; 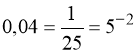 .
.
Тому: 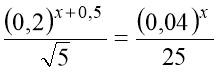
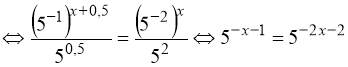 .
.
5) ![]() . (21)
. (21)
Помічаємо, що: 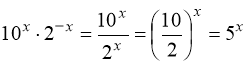 .
.
Тому: ![]()
![]() .
.
6) 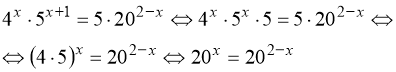
2.3. Рівняння виду
![]() , (22)
, (22)
де а ![]() R, а > 0, а ≠ 1, f = f(х) – деяка функція, є окремим випадком (при φ = 0) рівняння(9).
R, а > 0, а ≠ 1, f = f(х) – деяка функція, є окремим випадком (при φ = 0) рівняння(9).
Використовуючи означення нульового показника степеня, маємо:
1 = а0. Тому: (22) ![]() .
.
Корисно знати деякі записи одиниці:
![]()
![]()
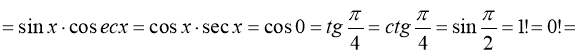 … і т.д.
… і т.д.
Приклад 13.
Розв’язати рівняння ![]() . (23)
. (23)
Розв’язання. Перетворимо: 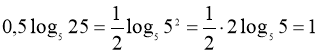 .
.
Тому![]()
![]()
![]() або
або ![]() .
.
Використовуючи правила перетворення степенів та основні властивості пропорції (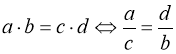 ), деякі рівняння вдається звести до рівняння виду (22).
), деякі рівняння вдається звести до рівняння виду (22).
Приклад 14.
Розв’язати рівняння ![]() . (24)
. (24)
Розв’язання. Перетворимо: 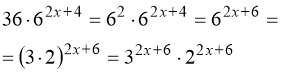 .
.
Тому:
![]()
![]()
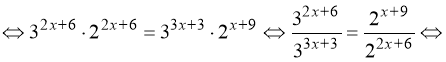
![]()
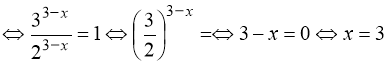 .
.
Приклад 15.
Розв’язати рівняння.
![]() (25)
(25)
Розв’язання. Використовуємо формулу: 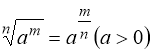 .
.
Тому:![]()
![]()
![]()
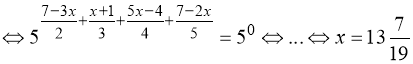 .
.
2.4. Рівняння виду
![]() , (26)
, (26)
де а ![]() R, а > 0, а ≠ 1; b
R, а > 0, а ≠ 1; b ![]() R, b > 0, b≠ 1; f = f(х), φ = φ(х) – деякі функції, у загальному випадку зводиться до рівняння (9) перетворенням його правої частини з використанням основної логарифмічної тотожності
R, b > 0, b≠ 1; f = f(х), φ = φ(х) – деякі функції, у загальному випадку зводиться до рівняння (9) перетворенням його правої частини з використанням основної логарифмічної тотожності ![]() . Тоді
. Тоді ![]() і рівняння (26) набуває вигляду:
і рівняння (26) набуває вигляду:
(26) ![]() .
.
Другий спосіб розв’язання рівняння (26) полягає в логарифмуванні обох його частин за довільною основою с
(с > 0, с ≠ 1):
(26) ![]() .
.
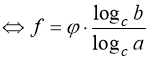 . (27)
. (27)
Якщо в якості с обрано основу b, або с = 10 або с = е (е – основа натурального логарифму), то розв’язок (27) рівняння (26) набуває виду:
(27) ![]() ;
;
(27) 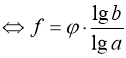 ;
;
(27) 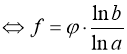
Приклад 16.
Розв’язати рівняння ![]() . (28)
. (28)
Розв’язання. Логарифмуємо обидві частини рівняння (28) за основою 10:
![]()
![]()
![]()
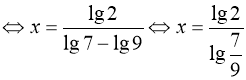 .
.
Приклад 17.
Розв’язати рівняння ![]() . (29)
. (29)
Розв’язання: Прологарифмуємо обидві частини рівняння (29) за основою 2:
![]()
![]()
![]() . (30)
. (30)
Після розкриття дужок і очевидних перетворень рівняння (30) зводиться до квадратного відносно х:
![]() , розв’язання якого звичайним способом цілком можливе, але пов’язане з великим об’ємом розрахунків. Однак, процес розв’язання рівняння (30) може бути істотно спрощений, якщо помітити, що квадратний тричлен
, розв’язання якого звичайним способом цілком можливе, але пов’язане з великим об’ємом розрахунків. Однак, процес розв’язання рівняння (30) може бути істотно спрощений, якщо помітити, що квадратний тричлен ![]() розкладається на лінійні множники:
розкладається на лінійні множники:
![]() .
.
Тоді: (30) ![]()
![]() . (31)
. (31)
Отримане рівняння (31) рівносильне сукупності двох рівнянь:
1) ![]() ;
;
2) 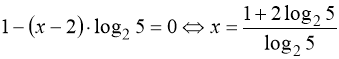 .
.
Відповідь: 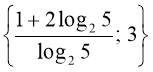 .
.
2.5. Рівняння виду
![]() , (32)
, (32)
де а ![]() R, а > 0, а ≠ 1; b
R, а > 0, а ≠ 1; b ![]() R, b > 0, b≠ 1; f = f(х), – деяка функція, основа степеня b не зводиться до основи степеня а, але показники обох степенів рівні.
R, b > 0, b≠ 1; f = f(х), – деяка функція, основа степеня b не зводиться до основи степеня а, але показники обох степенів рівні.
Покажемо, що рівняння (32) рівносильне рівнянню ![]() :
:
![]()
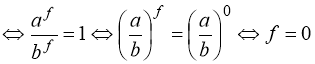 .
.
Приклад 18.
Розв’язати рівняння
![]() (33)
(33)
Розв’язання. Перенесемо в різні частини рівняння степені з різними основами:
![]()
![]()
![]()
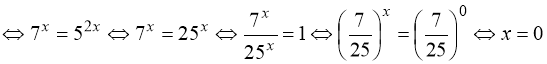 .
.
Відповідь: ![]() .
.
2.6. Рівняння виду
![]() , (34)
, (34)
де а > 0; а ≠ 1; f = f(х) – деяка функція: якщо b > 0 є окремим випадком (при φ = 1) рівняння (26);
якщо b ≤ 0 рівняння (34) розв’язків не має, так як при дійсних значеннях f степінь ![]() не може бути від’ємним або рівним нулю числом (на множині дійсних чисел
не може бути від’ємним або рівним нулю числом (на множині дійсних чисел ![]() ). Наприклад, рівняння
). Наприклад, рівняння ![]() розв’язків не має.
розв’язків не має.
Якщо а = 1 і b = 1 розв’язком рівняння (34) є область визначення (D) функції f:
![]() .
.
Якщо а = 1 і b ≠ 1 рівняння (34) розв’язків не має.
Якщо b > 0 в загальному випадку розв’язки рівняння (34) отримують логарифмуванням обох частин за основою а (а > 0; а ≠ 1):
![]()
![]() . (35)
. (35)
Інколи доцільно обидві частини рівняння (34) прологарифмувати за іншою основою с (с > 0; с ≠ 1) і, зокрема, за основами с = 10 або с = е (е – основа натурального логарифму):
![]()
![]()
![]()
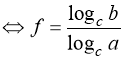 . (36)
. (36)
Аналогічно: 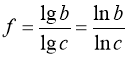 . (37)
. (37)
Також ми ліву та праву частину рівняння (34) можемо звести до однієї основи, використовуючи основну логарифмічну тотожність ![]() :
:
![]()
![]() .
.
Приклад 19.
Розв’язати рівняння
![]() . (38)
. (38)
Розв’язання. Прологарифмуємо обидві частини рівняння за основою 10:
![]()
![]()
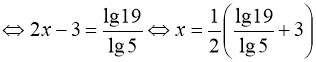 .
.
2.7. Рівняння виду
![]() …
… ![]() , (39)
, (39)
де а1, а2, … ап, b > 0; f1 = f1(х), f2 = f2(х), …, fп = fп(х)– деякі функції, є загальним випадком рівняння (34).
Логарифмуючи рівняння (39) за деякою основою с (с > 0; с ≠ 1) отримуємо рівняння (40), яке рівносильне рівнянню (39):
(39) ![]()
![]() .(40)
.(40)
Приклад 20.
Розв’язати рівняння
![]() . (41)
. (41)
Розв’язання. Прологарифмуємо обидві частини рівняння за основою 10:
![]()
![]()
![]()
![]()
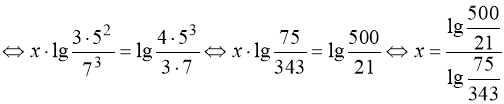 .
.
Приклад 21.
Розв’язати рівняння
![]() . (42)
. (42)
Розв’язання. Прологарифмуємо обидві частини рівняння за основою 10:
![]()
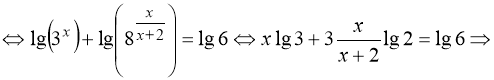
![]() . (43)
. (43)
Використані такі логарифмічні перетворення:
![]() ;
; 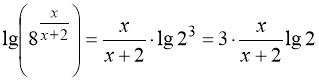 ;
;
![]() .
.
Рівняння (43) – квадратне відносно х, корені якого знаходяться за відомою формулою коренів квадратного рівняння:
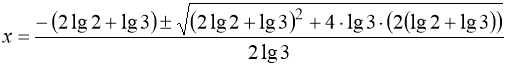 . (44)
. (44)
Перетворимо дискримінант формули (44):
![]()
![]() .
.
Тоді, враховуючи, що ![]() ,
,
Отримаємо:
(44) 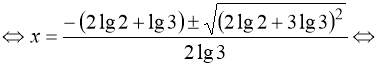
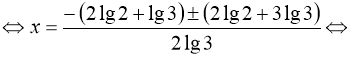
![]() або
або 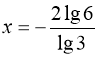 .
.
Відмітимо, що розв’язок рівняння (43) може бути істотно спрощено. Дійсно, уважний аналіз даного рівняння (42) дозволяє підібрати його очевидний розв’язок: х = 1. Отже, х = 1 є одним з двох коренів рівносильного йому рівняння (43). За теоремою Вієта для повного квадратного рівняння ![]() маємо:
маємо: 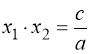 . Для рівняння (43) відомо, що х1 = 1;
. Для рівняння (43) відомо, що х1 = 1; ![]() ;
; ![]() .
.
Тому: 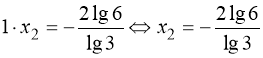 .
.
Відповідь: 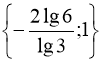 .
.
Додатковий коментар до розв’язування рівняння (42) – див. в кінці розділу.
2.8. Рівняння виду
![]()
![]() , (45)
, (45)
де А0, А1, …, Ап, k, т0, т1, …, тп ![]() R, а > 0; а ≠ 1, f = f(х) – деяка функція.
R, а > 0; а ≠ 1, f = f(х) – деяка функція.
Характерною властивістю рівняння (45) є наявність у показнику степеня (а) одного і того ж коефіцієнту (k) при функції f.
Для розв’язання рівняння (45) використовують перетворення: ![]() ,
, ![]() , …, та винесення за дужки у лівій частині рівняння спільного множника
, …, та винесення за дужки у лівій частині рівняння спільного множника ![]() :
:
(45) ![]() . (46)
. (46)
Позначимо сталу величину ![]() =с , тому:
=с , тому:
(46) 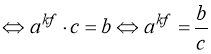 . (47)
. (47)
Якщо 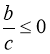 , то рівняння (47), а отже і рівносильне йому рівняння (46) розв’язків не має.
, то рівняння (47), а отже і рівносильне йому рівняння (46) розв’язків не має.
Якщо 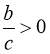 , то рівняння (47) є окремим випадком рівняння (34).
, то рівняння (47) є окремим випадком рівняння (34).
Приклад 22.
Розв’язати рівняння ![]() . (48)
. (48)
Розв’язання.
![]()
![]()
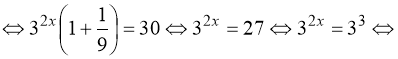
![]() .
.
Для спрощення обчислень інколи доцільно у рівнянні (45) винести за дужки множник ![]() , де ті – найменше з чисел
, де ті – найменше з чисел
т0, т1, … тп.
Приклад 23.
Розв’язати рівняння ![]() . (49)
. (49)
Розв’язання.
Перетворимо 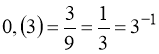 ;
; 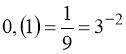 .
.
Тому: ![]() ;
;
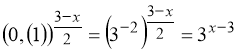 .
.
Рівняння (49) набуває вигляду:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Приклад 24.
Розв’язати рівняння ![]() . (50)
. (50)
Розв’язання.
Перетворимо: 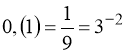 ;
;
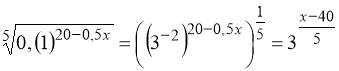 ;
;
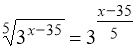 .
.
Тому:
![]()
![]() . (51)
. (51)
Перетворимо:
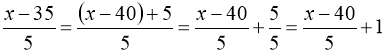 ;
;
![]() .
.
Тому:(51) ![]()
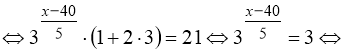
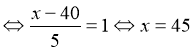 .
.
У рівняння виду (45) можуть входити дві різні основи, але при цьому, як правило, b = 0.
Приклад 25.
Розв’язати рівняння ![]() . (52)
. (52)
Розв’язання.
Характерною особливістю рівняння (52) є наявність двох основ (5 і 2), у показниках степенів, яких коефіцієнти при х рівні. Згрупуємо степені з однаковими основами в різних частинах рівняння і в кожному з них винесемо за дужки спільний множник (степені чисел 5 і 2, але обов’язково з однаковими показниками степеня):
![]()
![]()
![]()
![]() .
.
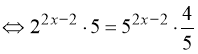 . (53)
. (53)
Використовуємо основну властивість пропорції 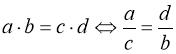 , перенесемо множники з невідомим у ліву частину, числа – у праву:
, перенесемо множники з невідомим у ліву частину, числа – у праву:
(53) 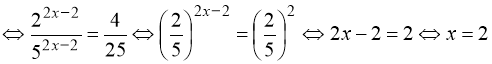 .
.
Наведемо декілька прикладів перетворення даних показникових рівнянь методом винесення за дужки спільного множника:
1) ![]()
![]()
![]() .
.
2) ![]()
![]()
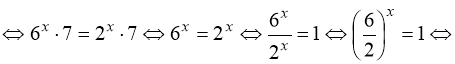
![]() .
.
Приклад 26.
Розв’язати рівняння
![]() . (54)
. (54)
Розв’язання. У правій частині рівняння (54) –сума нескінченно спадної геометричної прогресії b1; qb1; q2 b1; … , знаменник якої 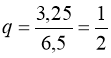 < 1. Сума її членів
< 1. Сума її членів 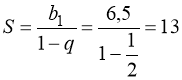 .
.
Тому:
![]()
![]()
![]()
![]() .
.
2.9. Рівняння виду
![]() , (55)
, (55)
де А, В, С, а ![]() R, А ≠ 0, а > 0, а ≠ 1, f = f(х) – деяка функція, заміною
R, А ≠ 0, а > 0, а ≠ 1, f = f(х) – деяка функція, заміною ![]() зводиться до квадратного рівняння
зводиться до квадратного рівняння
![]() , (56)
, (56)
а розв’язок рівняння (55) зводиться до розв’язання двох рівнянь: ![]() і
і ![]() , де у1 і у2 – корені (якщо вони існують)
, де у1 і у2 – корені (якщо вони існують)
рівняння (56).
Приклад 27.
Розв’язати рівняння
![]() . (57)
. (57)
Розв’язання. Перетворимо: ![]() ;
; ![]() .
.
Тому: ![]()
![]()
![]() . (58)
. (58)
Замінимо: ![]() . Тому:
. Тому:
(58) 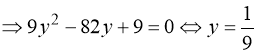 або
або ![]() .
.
Враховуючи заміну:
1) 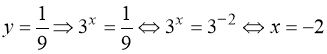 ;
;
2) ![]() .
.
Відповідь: ![]() .
.
Приклад 28.
Розв’язати рівняння
![]() . (59)
. (59)
Розв’язання. У шкільному курсі математики корінь п-ого степеня ![]() визначений тільки для натуральних значень п, тому слід вважати, що функція
визначений тільки для натуральних значень п, тому слід вважати, що функція ![]() визначена тільки для натуральних
визначена тільки для натуральних ![]() , а перетворення
, а перетворення 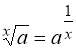 не є тотожністю (область визначення функції
не є тотожністю (область визначення функції 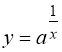 ширша, вона визначена для всіх х ≠ 0). Враховуючи це перейдемо від рівняння (59) до його наслідку (64 = 26):
ширша, вона визначена для всіх х ≠ 0). Враховуючи це перейдемо від рівняння (59) до його наслідку (64 = 26):
![]()
![]()
![]()
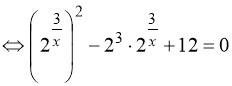 . (60)
. (60)
Заміна: 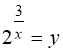 . Тому:
. Тому:
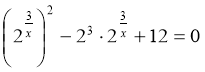
![]()
![]() або
або ![]() .
.
Враховуючи заміну:
1) 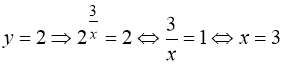 ;
;
2) 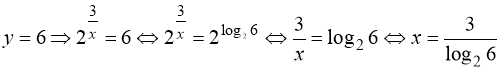 .
.
Корінь 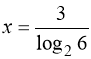 - сторонній, оскільки область визначення рівняння (59) – множина натуральних чисел
- сторонній, оскільки область визначення рівняння (59) – множина натуральних чисел ![]() .
.
Відповідь: ![]() .
.
Рівняння (55) є окремим випадком рівняння виду
![]() , яке заміною
, яке заміною ![]() зводиться до цілого раціонального алгебраїчного рівняння п-го степеня відносно у.
зводиться до цілого раціонального алгебраїчного рівняння п-го степеня відносно у.
Наведемо з коротким коментарем перетворення показникових рівнянь до рівняння виду (55)
1) ![]() .
.
2) 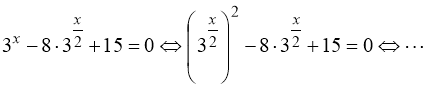 .
.
3) 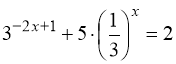 . (61)
. (61)
Перетворимо: 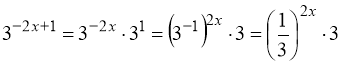 .
.
Замінимо: 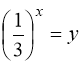 . Тому:
. Тому:
(61) ![]() або
або 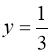 . Корінь
. Корінь ![]() - сторонній, оскільки
- сторонній, оскільки 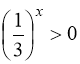 .
.
Враховуючи заміну: 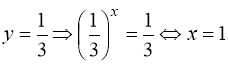 .
.
4) ![]() . (62)
. (62)
Помічаємо, що ![]()
![]() .
.
Заміна: ![]() . Тому:
. Тому:
![]()
![]()
![]() або
або 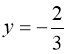 .
.
Корінь 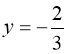 - сторонній.
- сторонній.
Враховуючи заміну: ![]()
![]()
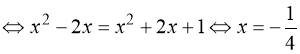 .
.
Приклад 29.
Розв’язати рівняння
![]() (63)
(63)
Розв’язання. Враховуємо, що ![]() . Тому:
. Тому:
![]() .
.
Заміна: ![]() . Тому:
. Тому:
(63) ![]()
![]() або
або ![]() .
.
Враховуючи заміну:
1) ![]() ,
, ![]() .
.
2) ![]() Ø.
Ø.
Відповідь: ![]() .
.
Приклад 30.
Розв’язати рівняння
![]() (64)
(64)
Розв’язання.
Заміна: ![]() . Тому:
. Тому:
![]()
![]() . (65)
. (65)
Рівняння (65) – ірраціональне. Піднесемо обидві частини рівняння (65) до другого степеня. Нагадуємо, що при цьому можуть з’явитися сторонні корені, які виключаються перевіркою. Втрати коренів відбутися не може.
![]()
![]()
![]()
![]() або
або ![]() .
.
у = -1 є стороннім коренем, що встановлюємо перевіркою. Отже, враховуючи заміну:
![]() ;
;
Відповідь: ![]() .
.
2.10. Рівняння виду
![]() , (66)
, (66)
де А, В, С ![]() R; А ≠ 0; f = f(х) – деяка функція, основи а і b є взаємно оберненими додатними числами (а · b = 1). Заміною:
R; А ≠ 0; f = f(х) – деяка функція, основи а і b є взаємно оберненими додатними числами (а · b = 1). Заміною: 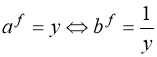 рівняння (66) зводиться до рівняння (56):
рівняння (66) зводиться до рівняння (56):
(66) 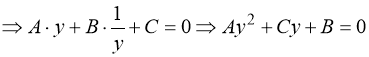 .
.
У деяких навчальних посібниках рівняння (66), якщо а · b = 1 зводиться до виду:
![]() (67)
(67)
Приклад 31.
Розв’язати рівняння
![]() (68)
(68)
Розв’язання. Помічаємо, що ![]() , тобто основи степенів рівняння (68) – взаємно обернені додатні числа.
, тобто основи степенів рівняння (68) – взаємно обернені додатні числа.
Перетворимо: 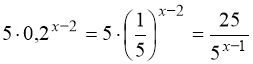 .
.
Заміна: ![]() . Тому:
. Тому:
![]()
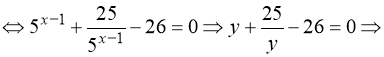
![]() або
або ![]() .
.
Враховуючи заміну:
1) ![]() ;
;
2) ![]() .
.
Відповідь: ![]() .
.
Наведемо з короткими коментарями перетворення показникових рівнянь до рівняння виду (66) або (67) :
1) ![]() . (69)
. (69)
Перетворимо: 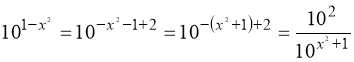 .
.
Заміна: ![]() . Тому:
. Тому:
(69) 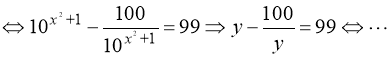 .
.
2) 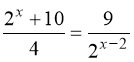 .
.
Перетворимо:
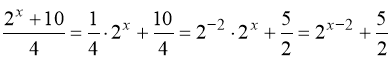 . (70)
. (70)
Замінимо: ![]() . Тому:
. Тому:
(70) 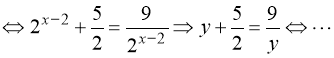 .
.
3) ![]() . (71)
. (71)
Перетворимо: ![]() ;
;
![]() .
.
Заміна: ![]() . Тому:
. Тому:
(71) ![]()
![]() .
.
Приклад 32.
Розв’язати рівняння
![]() . (72)
. (72)
Розв’язання. Помічаємо, що ![]() , тобто основи степенів рівняння (72) – взаємно обернені додатні числа і рівняння (72) є окремим випадком рівняння (66).
, тобто основи степенів рівняння (72) – взаємно обернені додатні числа і рівняння (72) є окремим випадком рівняння (66).
Заміна: ![]() , тоді
, тоді 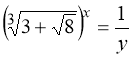 , і рівняння (72) набуває вигляду:
, і рівняння (72) набуває вигляду:
![]()
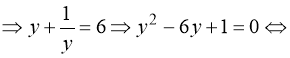
![]() або
або ![]() .
.
Враховуємо заміну:
1) ![]()
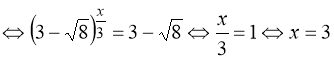 ;
;
2) ![]()
![]() . (73)
. (73)
Оскільки ![]() , то:
, то:
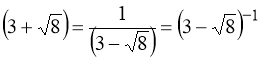 . Тоді:
. Тоді:
(73) ![]()
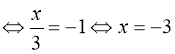 .
.
Відповідь: ![]() .
.
Наведемо з короткими коментарями декілька перетворень рівнянь виду (72):
1) ![]() . Помічаємо, що
. Помічаємо, що
![]() .
.
Заміна: ![]() ;
; ![]()
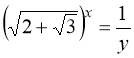 .
.
Тоді 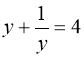 і т.д.
і т.д.
2) ![]() . Помічаємо: що
. Помічаємо: що
![]() і т.д.
і т.д.
3) ![]() . Помічаємо, що
. Помічаємо, що
![]() , і т.д.
, і т.д.
Корисно знати і «впізнавати» деякі «заховані» в умовах показникових рівнянь записи одиниці:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Як правило, такі записи одиниці є окремими випадками
(для а > 1) тотожності:
![]() .
.
Розглянемо ще один спосіб розв’язання рівняння типу (66).
Приклад 33.
Розв’язати рівняння
![]() . (74)
. (74)
Розв’язання. Заміна: ![]() ;
;
![]() . Помічаємо, що
. Помічаємо, що ![]() . Тоді:
. Тоді:
![]()
![]()
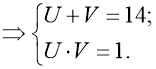
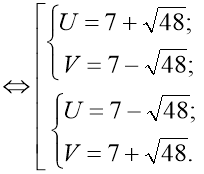
Враховуємо заміну:
1) 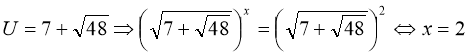 ;
;
2) 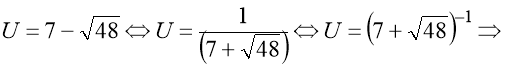
![]() ;
;
Відмітимо, що заміна у вигляді ![]() ,
, ![]() також приведе до отримання попереднього результату.
також приведе до отримання попереднього результату.
Відповідь: ![]() .
.
2.11. Рівняння виду
![]() , (75)
, (75)
де А, В, С ![]() R, А ≠ 0, f = f(х) – деяка функція; основи а, b, с задовольняють умову:
R, А ≠ 0, f = f(х) – деяка функція; основи а, b, с задовольняють умову: ![]() , тобто є трьома послідовними членами геометричної прогресії.
, тобто є трьома послідовними членами геометричної прогресії.
Рівняння (75) діленням на одну із крайніх степенів (![]() або
або ![]() ) і подальшою заміною зводиться до квадратного рівняння виду (56). У деяких навчальних посібниках рівняння (75) при
) і подальшою заміною зводиться до квадратного рівняння виду (56). У деяких навчальних посібниках рівняння (75) при ![]() зводиться до вигляду:
зводиться до вигляду:
![]() . (76)
. (76)
Приклад 34.
Розв’язати рівняння
![]() . (77)
. (77)
Розв’язання. Помічаємо, що числа 4, 6 і 9 трьома послідовними членами геометричної прогресії (62 = 4 · 9). Показники степенів (2х) однакові, тобто рівняння (77) є окремим випадком рівняння (75). Почленно поділимо обидві частини рівняння (77) на ![]() :
:
![]()
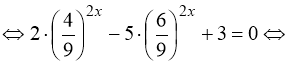
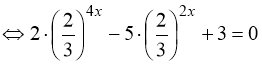 . (78)
. (78)
Заміна: 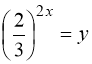 . Тому:
. Тому: 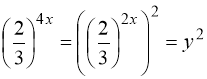 .
.
(78) ![]() або
або 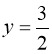 .
.
Враховуємо заміну:
1) 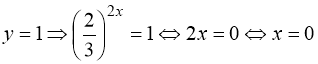 ;
;
2) 
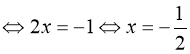 .
.
Відповідь: 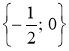 .
.
Наведемо декілька прикладів перетворення рівнянь до виду, коли є очевидним, що це – окремий випадок рівняння (75) або (76).
1) 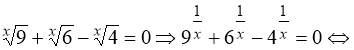
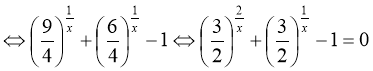 .
.
2) ![]()
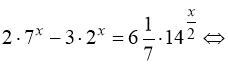
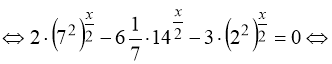
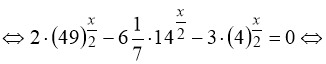
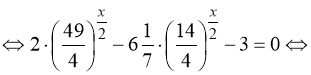
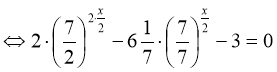 .
.
3) ![]()
![]()
![]()
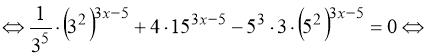
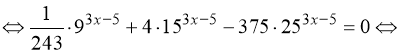
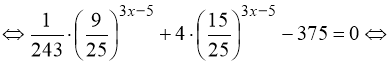
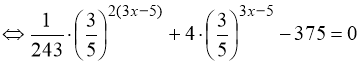 .
.
4) ![]()
![]()
![]()
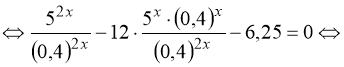
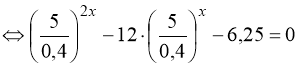 .
.
Приклад 35.
Розв’язати рівняння
![]() . (79)
. (79)
Розв’язання. При розв’язуванні рівняння (79) послідовно використаємо дві заміни.
Помічаємо: що ![]() ;
;
![]() .
.
Тому: ![]()
![]()
![]() . (80)
. (80)
Перша заміна: ![]() .
.
Тому:
(80) ![]()
![]() . (81)
. (81)
Очевидно, що рівняння (81) – окремий випадок рівняння (76). Розділимо ліву і праву частини рівняння (81) на ![]() :
:
(81) 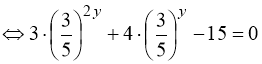 . (82)
. (82)
Друга заміна: 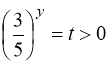 . Тому:
. Тому:
(82) ![]() - сторонній корінь, або
- сторонній корінь, або ![]() .
.
Враховуємо другу заміну:
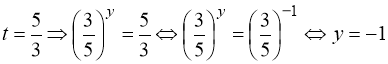 .
.
Враховуємо першу заміну:
![]() або
або ![]() .
.
Відповідь: ![]() .
.
Якщо обидві частини рівняння (75) розділити на ![]() , то воно зводиться до рівняння виду (67).
, то воно зводиться до рівняння виду (67).
Приклад 36.
Розв’язати рівняння
![]() . (83)
. (83)
Розв’язання. Помічаємо, що 362 = 16 · 81, показники степенів чисел 16, 36 і 81 однакові, тобто рівняння (83) – окремий випадок рівняння (75). Почленно поділимо обидві частини рівняння (83) на ![]() :
:
![]()
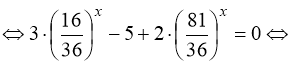
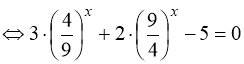 . (84)
. (84)
Помічаємо, що 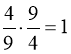 , тобто рівняння (84) – окремий випадок рівняння (66). Заміна:
, тобто рівняння (84) – окремий випадок рівняння (66). Заміна: 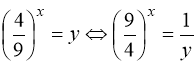 і рівняння (84) набуває вигляду:
і рівняння (84) набуває вигляду: 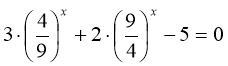
![]()
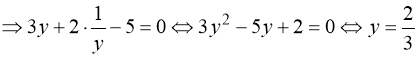 або
або ![]() .
.
Враховуємо заміну, і т.д.
Відповідь: 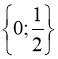 .
.
Рівняння (75) є окремим випадком рівняння, однорідного відносно ![]() і
і ![]() :
:
![]()
![]() . (85)
. (85)
«Однорідність» рівняння (85) полягає у тому, що всі одночлени містять добутки степенів двох різних основ (а і b), причому сума показників степенів у кожному одночлені є величина стала (nf), наприклад:
![]() ;
; ![]() і т.д.
і т.д.
Почленно розділивши обидві частини рівняння (85) на ![]() і замінивши
і замінивши 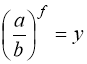 , отримаємо алгебраїчне рівняння п-го степеня відносно у. Цікавими є випадки якщо п = 2 (див. приклад 34) та
, отримаємо алгебраїчне рівняння п-го степеня відносно у. Цікавими є випадки якщо п = 2 (див. приклад 34) та
п = 3 (див. приклад 37).
Приклад 37.
Розв’язати рівняння
![]() . (86)
. (86)
Розв’язання. Рівняння (86) є окремим випадком рівняння (85), у якому п = 3; f = х; а = 2; b = 5. Почленно поділимо обидві частини рівняння(86)на![]() :
: ![]()
![]()
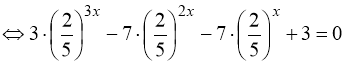 . (87)
. (87)
Заміна: 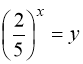 . Тому:
. Тому:
(87) ![]()
![]()
![]()
![]() або
або
![]() , або
, або ![]() , або
, або 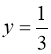 .
.
У виконаних перетвореннях використана формула розкладання суми кубів: ![]() .
.
Враховуємо заміну:
1) 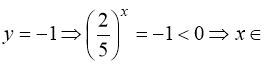 Ø;
Ø;
2) 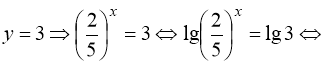
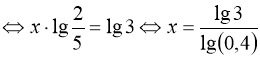 ;
;
3) 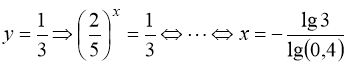 .
.
Відповідь: 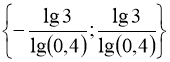 .
.
Приклад 38.
Розв’язати рівняння
![]() . (88)
. (88)
Розв’язання. Область допустимих значень рівняння (88) – множина натуральних чисел (х ![]() N), більших за одиницю (х ≥ 2). З врахуванням цього перейдемо від рівняння (88) до його наслідків:
N), більших за одиницю (х ≥ 2). З врахуванням цього перейдемо від рівняння (88) до його наслідків:
![]()
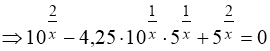 . (89)
. (89)
Рівняння (89) – однорідне рівняння виду (76) при п = 2. Почленно розділимо обидві частини рівняння (89) на ![]() і введемо заміну:
і введемо заміну: 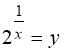 . Тому:
. Тому:
(89) 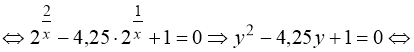
![]() або
або 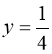 .
.
Враховуємо заміну:
1)  ;
;
2) 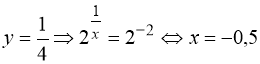 .
.
Обидва знайдені корені – сторонні, так як х ![]() N та х ≥ 2.
N та х ≥ 2.
Відповідь: {х ![]() Ø}.
Ø}.
Відмітимо, що якщо б рівняння (88) було записано у вигляді:
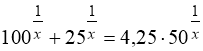 ,
,
То його коренями були б числа х = 0,5 і х = –0,5, так як область визначення цього рівняння – всі раціональні числа.
2.12. Використання властивостей монотонності функції при розв’язанні показникових рівнянь
При розв’язанні деяких видів показникових рівнянь використовують наступні властивості монотонності функції:
1) показникова функція ![]() з основою, більшою одиниці
з основою, більшою одиниці ![]() , є монотонно зростаючою, тобто якщо
, є монотонно зростаючою, тобто якщо ![]() і
і ![]() , то
, то ![]() ;
;
2) показникова функція ![]() з додатною основою, меншою за одиницю
з додатною основою, меншою за одиницю ![]() , є монотонно спадною, тобто якщо
, є монотонно спадною, тобто якщо ![]() і
і ![]() , то
, то ![]() ;
;
3) якщо функції f і φ обидві зростаючі (спадні) на множині М, то функція f + φ також зростаюча (спадна) на цій множині. Наприклад, функція 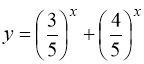 є монотонно спадною.
є монотонно спадною.
Нагадаємо, що будь-яка монотонна функція приймає конкретне числове значення тільки при одному значенні аргументу. Наприклад, якщо монотонно спадна функція 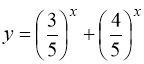 при х = 2 приймає значення у = 1, то ні при якому іншому значенні х ця функція не дорівнює одиниці.
при х = 2 приймає значення у = 1, то ні при якому іншому значенні х ця функція не дорівнює одиниці.
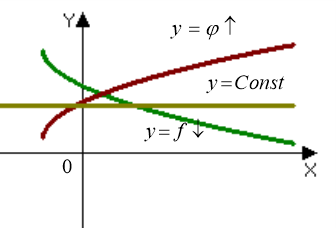
Рис. 2.1
Не більш, ніж в одній точці перетинаються графіки:
-
спадної
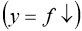 і зростаючої
і зростаючої  функції (рис. 2.1);
функції (рис. 2.1);
-
спадної
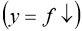 і сталої
і сталої 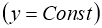 функції. (рис. 2.1);
функції. (рис. 2.1);
-
зростаючої
 і сталої
і сталої 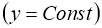 функції. (рис. 2.1).
функції. (рис. 2.1).
Можливі варіанти, коли в кожному з трьох перерахованих випадків графіки функцій не перетинаються.
Приклад 39.
Розв’язати рівняння
![]() . (90)
. (90)
Розв’язання. Розділимо обидві частини рівняння (90) на ![]() :
:
![]()
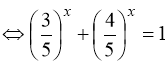 . (91)
. (91)
Розв’язання рівняння (91) і аналогічних йому складаються з двох етапів. По-перше, треба «здогадатись» і методом підбору знайти одне очевидне розв’язання рівняння (91). По-друге, погодившись на властивості 1 … 3 монотонності функції, довести, що інших розв’язків не може бути.
Очевидний розв’язок рівняння (91) х = 2. Дійсно: 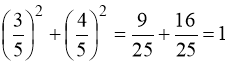 . Доведемо, що інших розв’язків не має.
. Доведемо, що інших розв’язків не має.
Кожна із функцій 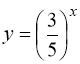 і
і 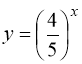 як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Отже, при
як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Отже, при ![]() ліва частина рівняння (91) менша за одиницю, при
ліва частина рівняння (91) менша за одиницю, при ![]() - більша за одиницю. Таким чином доведено, що х = 2 – єдиний розв’язок рівняння (91).
- більша за одиницю. Таким чином доведено, що х = 2 – єдиний розв’язок рівняння (91).
У деяких навчальних посібниках наводиться таке доведення єдності (х = 2) розв’язання рівняння типу (91). Розглянемо два випадки:
1) Нехай ![]() . Тому:
. Тому:
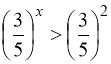 , (92)
, (92)
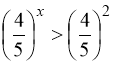 . (93)
. (93)
Додавши нерівності (92) і (93), отримаємо:
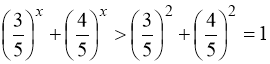 ,
,
тобто при ![]() завжди
завжди 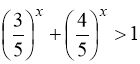 і серед чисел
і серед чисел ![]() рівняння (91) коренів не має.
рівняння (91) коренів не має.
2) Нехай ![]() . Тоді:
. Тоді:
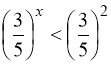 , (94)
, (94)
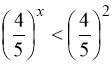 . (95)
. (95)
Додавши нерівності (94) і (95), отримаємо:
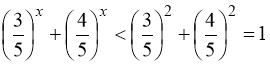 ,
,
тобто при ![]() завжди
завжди 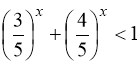 і серед чисел
і серед чисел ![]() рівняння (91) коренів не має.
рівняння (91) коренів не має.
Таким чином, х = 2 – єдиний корінь рівняння (91).
Відповідь: ![]() .
.
Наведемо з короткими коментарями декілька аналогічних прикладів.
1) ![]() . Очевидне розв’язання х = 3. Зліва – сума двох монотонно зростаючих функцій.
. Очевидне розв’язання х = 3. Зліва – сума двох монотонно зростаючих функцій.
2) 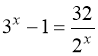 . Очевидний розв’язок х = 2. Зліва – монотонно зростаюча функції, справа – монотонно спадна.
. Очевидний розв’язок х = 2. Зліва – монотонно зростаюча функції, справа – монотонно спадна.
3) 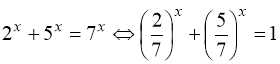 . Очевидний розв’язок х = 1. Зліва – монотонно спадна функції, справа – стала.
. Очевидний розв’язок х = 1. Зліва – монотонно спадна функції, справа – стала.
4) 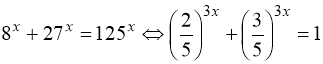 . Очевидний розв’язок
. Очевидний розв’язок 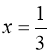 . Зліва – монотонно спадна функція, справа – стала.
. Зліва – монотонно спадна функція, справа – стала.
5) ![]() . Очевидний розв’язок х = 5. Зліва – монотонно спадна функції
. Очевидний розв’язок х = 5. Зліва – монотонно спадна функції 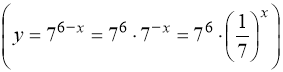 , справа – монотонно зростаюча функція
, справа – монотонно зростаюча функція ![]() . Графіки монотонно спадної і монотонно зростаючої функцій перетинаються не більше одного разу, тобто корінь х = 5 – єдиний.
. Графіки монотонно спадної і монотонно зростаючої функцій перетинаються не більше одного разу, тобто корінь х = 5 – єдиний.
Приклад 40.
Розв’язати рівняння
![]() . (96)
. (96)
Розв’язання. Очевидний розв’язок х = 2. Доведемо, що інших розв’язків не має. Розділимо обидві частини рівняння (96) на ![]() :
:
![]()
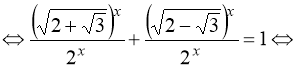
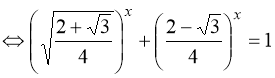 . (97)
. (97)
Основа степенів в лівій частині рівняння (97) менша за одиницю 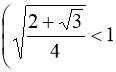 і
і 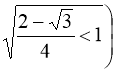 , тобто в лівій частині рівняння (97) – монотонно спадна функція, в правій частині – стала функція (одиниця). Відомо, що графіки монотонно спадної функції і сталої функції перетинаються не більше одного разу, тобто знайдений корінь х = 2 – єдиний корінь рівняння (96). Відповідь:
, тобто в лівій частині рівняння (97) – монотонно спадна функція, в правій частині – стала функція (одиниця). Відомо, що графіки монотонно спадної функції і сталої функції перетинаються не більше одного разу, тобто знайдений корінь х = 2 – єдиний корінь рівняння (96). Відповідь: ![]() .
.
Приклад 41.
Розв’язати рівняння
![]() . (98)
. (98)
Значення х = 2 є розв’язком цього рівняння: ![]() . Доведемо, що інших розв’язків це рівняння не має. Функції
. Доведемо, що інших розв’язків це рівняння не має. Функції ![]() та
та ![]() монотонно зростають при всіх значеннях х. Тому, якщо
монотонно зростають при всіх значеннях х. Тому, якщо ![]() , то
, то ![]() ,
, ![]() , сума
, сума ![]() , тобто при
, тобто при ![]() рівняння (98) не має розв’язків. Якщо
рівняння (98) не має розв’язків. Якщо ![]() , то
, то ![]() ,
, ![]() , сума
, сума ![]() , отже, при
, отже, при ![]() рівняння (98) також не має розв’язків. Звідси випливає, що дане рівняння (98) має єдиний розв’язок х = 2.
рівняння (98) також не має розв’язків. Звідси випливає, що дане рівняння (98) має єдиний розв’язок х = 2.
Відповідь: 2.
Приклад 42.
Розв’язати рівняння
![]() . (99)
. (99)
Поділимо рівняння(99) на ![]() , дістанемо
, дістанемо 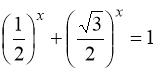 . Оскільки
. Оскільки 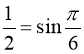 ,
, 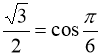 , то рівність
, то рівність 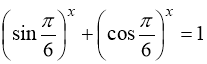 справджується при х = 2. Доведемо, що інших розв’язків рівняння(99) не має. Дійсно, функції
справджується при х = 2. Доведемо, що інших розв’язків рівняння(99) не має. Дійсно, функції 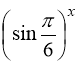 та
та 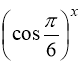 монотонно спадні при всіх значеннях х, тому
монотонно спадні при всіх значеннях х, тому
при ![]() виконується нерівність
виконується нерівність 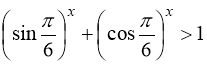 ,
,
а при ![]() - нерівність
- нерівність 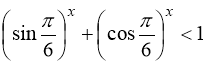 . Отже, рівняння (99) має єдиний розв’язок х = 2.
. Отже, рівняння (99) має єдиний розв’язок х = 2.
Відповідь: 2.
Відмітимо, що після розв’язання рівняння методом підбору («вгадування») коренів обов’язково необхідний етап доведення єдиності знайденого розв’язання. У протилежному випадку розв’язання рівняння буде неповним і виникне небезпека втрати коренів. Наведемо відомий в літературі приклад помилкового «розв’язання» рівняння методом підбору.
На іспиті рівняння (42) було «розв’язане» так:
(42) ![]() . (100)
. (100)
У цьому випадку легко впізнати, що х = 1 – корінь рівняння (100). Відповідь х = 1 було названо абітурієнтами без якого-небудь доведення єдиності знайденого розв’язку (таке доведення взагалі неможливе).
ІІІ. Розв’язування степенево-показникових рівнянь
Рівняння виду
![]() , (101)
, (101)
де f = f(х), φ1 = φ1(х), φ2 = φ2(х) – деякі функції, є степенево-показниковим.
Нагадаємо, що область визначення степенево-показникової функції ![]() можна знайти, розглядаючи три випадки:
можна знайти, розглядаючи три випадки:
1. ![]() , φ – довільне число; (102)
, φ – довільне число; (102)
2. ![]() , φ – ціле число; (103)
, φ – ціле число; (103)
3. ![]() , φ – ціле число або дробове додатне число; (104)
, φ – ціле число або дробове додатне число; (104)
Якщо відомо, що ![]() і
і ![]() , то рівняння (101) зводиться до показникового рівняння виду (9) і розв’язується за допомогою прирівнювання показників: φ1 = φ2. Якщо за умовою не виключаються випадки
, то рівняння (101) зводиться до показникового рівняння виду (9) і розв’язується за допомогою прирівнювання показників: φ1 = φ2. Якщо за умовою не виключаються випадки ![]() і
і ![]() , то слід розглядати декілька випадків і розв’язання рівняння (101) зводиться до розв’язання наступних рівнянь (з подальшою перевіркою отриманих результатів і з врахуванням того, що вираз
, то слід розглядати декілька випадків і розв’язання рівняння (101) зводиться до розв’язання наступних рівнянь (з подальшою перевіркою отриманих результатів і з врахуванням того, що вираз ![]() і 00 не має змісту):
і 00 не має змісту):
1. ![]() . При цьому рівняння (101) набуває вигляду
. При цьому рівняння (101) набуває вигляду ![]() , яке перетворюється у правильну рівність при будь-яких допустимих значеннях функції φ1 і φ2. Іншими словами, корені рівняння
, яке перетворюється у правильну рівність при будь-яких допустимих значеннях функції φ1 і φ2. Іншими словами, корені рівняння ![]() будуть коренями даного рівняння (101), якщо вони одночасно належать областям визначення функцій φ1 = φ1(х), φ2 = φ2(х).
будуть коренями даного рівняння (101), якщо вони одночасно належать областям визначення функцій φ1 = φ1(х), φ2 = φ2(х).
Схема розв’язання:
а) знаходимо корені рівняння ![]() ;
;
б) перевірка: корені рівняння ![]() повинні належати областям визначення функцій φ1 і φ2.
повинні належати областям визначення функцій φ1 і φ2.
2. ![]() . При цьому рівняння (101) набуває вигляду
. При цьому рівняння (101) набуває вигляду ![]() , яке перетворюється у правильну рівність тільки в випадках, якщо значення функцій φ1 і φ2 одночасно або парні, або не парні (наприклад, якщо φ1 = 6 і φ2 = 8, то
, яке перетворюється у правильну рівність тільки в випадках, якщо значення функцій φ1 і φ2 одночасно або парні, або не парні (наприклад, якщо φ1 = 6 і φ2 = 8, то ![]() ; якщо φ1 = 5 і φ2 = 7, то
; якщо φ1 = 5 і φ2 = 7, то ![]() ).
).
Нагадаємо, що у шкільному курсі математики степені з від’ємними основами і дробовими показниками не розглядаються (наприклад, вираз ![]() або
або ![]() не має змісту). Іншими словами, корені рівняння
не має змісту). Іншими словами, корені рівняння ![]() будуть коренями даного рівняння (101) тільки в тому випадку, якщо відповідні їм значення функцій φ1 і φ2 будуть цілими числами однакової парності (або обидва парні, або обидва не парні).
будуть коренями даного рівняння (101) тільки в тому випадку, якщо відповідні їм значення функцій φ1 і φ2 будуть цілими числами однакової парності (або обидва парні, або обидва не парні).
Схема розв’язання:
а) знаходимо корені рівняння ![]() ;
;
б) перевірка: корені рівняння ![]() почерзі підставляють у функції φ1 і φ2. Числові значення функцій φ1 і φ2 для кожного з цих коренів повинні бути цілими числами однакової парності.
почерзі підставляють у функції φ1 і φ2. Числові значення функцій φ1 і φ2 для кожного з цих коренів повинні бути цілими числами однакової парності.
3. ![]() . При цьому рівняння (101) набуває вигляду
. При цьому рівняння (101) набуває вигляду ![]() , яке перетворюється у правильну рівність у випадку, якщо числові значення функцій φ1 і φ2 або цілі додатні числа, або додатні дроби виду
, яке перетворюється у правильну рівність у випадку, якщо числові значення функцій φ1 і φ2 або цілі додатні числа, або додатні дроби виду ![]() , де т – ціле число, п – натуральне число (наприклад, правильною рівністю є:
, де т – ціле число, п – натуральне число (наприклад, правильною рівністю є: ![]() ,
, ![]() ). Нагадаємо, що вираз
). Нагадаємо, що вираз ![]()
![]()
![]() і
і ![]() при цілих від’ємних k (також, як і при k = 0) і при
при цілих від’ємних k (також, як і при k = 0) і при 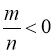 змісту не має. Іншими словами, корені рівняння
змісту не має. Іншими словами, корені рівняння ![]() будуть коренями даного рівняння (101) тільки в тому випадку, якщо значення функцій φ1 і φ2 від цих коренів – додатні цілі числа або додатній дріб
будуть коренями даного рівняння (101) тільки в тому випадку, якщо значення функцій φ1 і φ2 від цих коренів – додатні цілі числа або додатній дріб ![]() , де
, де ![]() ,
, ![]() (тобто додатне раціональне число).
(тобто додатне раціональне число).
Схема розв’язання:
а) знаходимо корені рівняння ![]() ;
;
б) перевірка: корені рівняння ![]() почерзі підставляємо у функції φ1 і φ2. Числові значення функцій φ1 і φ2 для кожного із цих коренів повинно бути або додатними цілими числами, або додатними раціональними числами.
почерзі підставляємо у функції φ1 і φ2. Числові значення функцій φ1 і φ2 для кожного із цих коренів повинно бути або додатними цілими числами, або додатними раціональними числами.
4. φ1 = φ2. Корені цього рівняння будуть коренями даного рівняння (101), якщо вони належать області визначення (102) … (104) цього рівняння.
Схема розв’язання:
а) знаходимо корені рівняння φ1 = φ2;
б) перевірка: корені рівняння φ1 = φ2 почергово підставляємо у дане рівняння (101) і перевіряємо дотримання умов (102) … (104).
Приклад 43.
Розв’язати рівняння
![]() . (105)
. (105)
Розв’язання. Це окремий випадок рівняння (99), де ![]() ;
; ![]() ;
;![]() .
.
Розглянемо чотири випадки:
1) ![]() . Перевірка: знайдене значення х = 2 підставляємо у рівняння (105): 12 = 10
. Перевірка: знайдене значення х = 2 підставляємо у рівняння (105): 12 = 10 ![]() 1 = 1, тобто х = 2 – корінь рівняння (103).
1 = 1, тобто х = 2 – корінь рівняння (103).
2) ![]() . Перевірка: знайдене значення х = 0 підставляємо у рівняння (105):
. Перевірка: знайдене значення х = 0 підставляємо у рівняння (105): ![]() , тобто х = 0 – корінь рівняння (103).
, тобто х = 0 – корінь рівняння (103).
3) ![]() . Перевірка: знайдене значення х = 1 підставляємо у рівняння (105):
. Перевірка: знайдене значення х = 1 підставляємо у рівняння (105): ![]() . Вираз 0-1 не має змісту, тобто х = 1 не є коренем рівняння (105).
. Вираз 0-1 не має змісту, тобто х = 1 не є коренем рівняння (105).
4) ![]() або
або ![]() . Перевірка: один корінь (х = 0) перевірено при розгляданні другого випадку. Перевіряємо другий корінь:
. Перевірка: один корінь (х = 0) перевірено при розгляданні другого випадку. Перевіряємо другий корінь: ![]() , тобто
, тобто ![]() - корінь рівняння (105).
- корінь рівняння (105).
Відповідь: ![]() .
.
Приклад 44.
Розв’язати рівняння
![]() . (106)
. (106)
Деякі автори посібників, наприклад ![]() вважають, що рівняння(106) визначене, якщо основа
вважають, що рівняння(106) визначене, якщо основа ![]() , тобто при
, тобто при ![]() . Рівність степенево-показникових функцій з однією основою справджується, якщо основа дорівнює одиниці, або основа відмінна від одиниці, проте додатна, а показники степенів рівні. Отже, рівняння(106) рівносильне сукупності
. Рівність степенево-показникових функцій з однією основою справджується, якщо основа дорівнює одиниці, або основа відмінна від одиниці, проте додатна, а показники степенів рівні. Отже, рівняння(106) рівносильне сукупності
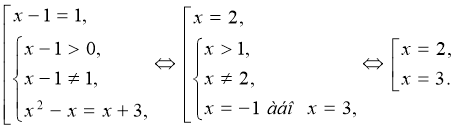
При ![]() основа
основа ![]()
![]() - від’ємна, це значення не належить області визначення.
- від’ємна, це значення не належить області визначення.
Відповідь: ![]() .
.
Приклад 45.
Розв’язати рівняння.
![]() . (107)
. (107)
При х = 2 маємо в обох частинах рівняння(107) 00, цей вираз невизначений, отже, ![]() . Розв’язуємо рівносильну сукупність рівнянь
. Розв’язуємо рівносильну сукупність рівнянь
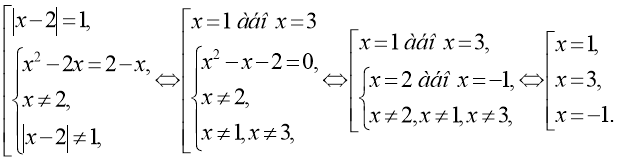
Відповідь: ![]() .
.
Приклад 46.
Розв’язати рівняння.
![]() . (108)
. (108)
ОДЗ: 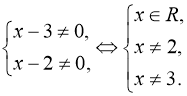 .
.
Ліва частина рівняння(108) дорівнює одиниці, якщо показник степеня дорівнює нулю, а основа додатна, або основа рівна одиниці, а показник степеня визначений. Тобто рівняння(108) рівносильне сукупності рівнянь
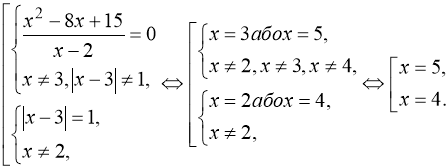
Відповідь: ![]() .
.
Приклад 47.
Розв’язати рівняння.
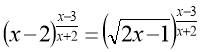 . (109)
. (109)
Показник степеня в обох частинах рівняння(109) однаковий, тому рівність можлива тоді, коли він дорівнює нулю, а основи додатні, або коли основи додатні і рівні між собою, а показник степеня визначений. Таким чином, рівняння(109) рівносильне сукупності двох систем:
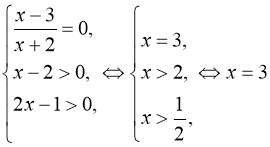 ;
;
або
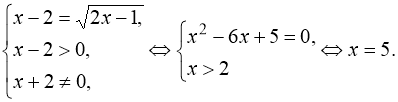
Відповідь: ![]() .
.
Окремим випадком рівняння (103) є рівняння виду:
![]() , (110)
, (110)
при розв’язанні якого випадок ![]() можна не розглядати, так як ні при яких значеннях φ рівність 0φ = 1 неможлива
можна не розглядати, так як ні при яких значеннях φ рівність 0φ = 1 неможлива ![]() , а випадок φ1 = φ2 вироджується у φ = 0 (формальне перетворення:
, а випадок φ1 = φ2 вироджується у φ = 0 (формальне перетворення: ![]() , тоді
, тоді ![]() ).
).
Приклад 48.
Розв’язати рівняння
![]() . (111)
. (111)
Розв’язання. Це окремий випадок рівняння (110), у якому ![]() ;
; ![]() . Розглянемо три випадки:
. Розглянемо три випадки:
1) ![]() .
.
2) ![]() .
.
3) ![]() або х = 1.
або х = 1.
Перевіркою переконуємось, що всі знайдені корені задовольняють рівняння (111).
Відповідь: ![]()
ІV. Розв’язування показникових рівнянь
(за збірником ДПА)
Варіант 1.
Завдання 4.1. При яких значеннях параметра а рівняння ![]() має тільки один дійсний корінь?
має тільки один дійсний корінь?
Розв’язання. Зробимо заміну ![]() ,
, ![]() , тоді рівняння рівносильне системі :
, тоді рівняння рівносильне системі : 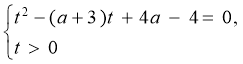
Задача звелася до знаходження додатних розв’язків квадратного рівняння з параметром а.
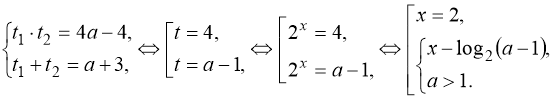
Дане рівняння має єдиний корінь, якщо 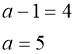 або
або 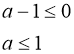 .
.
Відповідь: Рівняння має єдиний дійсний корінь при ![]() або
або ![]() .
.
Варіант 4.
Завдання 4.2.
Розв’язання.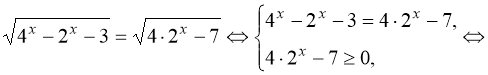
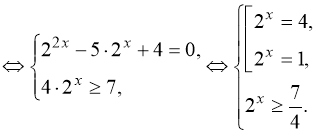 тому
тому 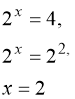 .
.
Відповідь: 2.
Варіант 5.
Завдання 4.1.
Розв’яжіть рівняння
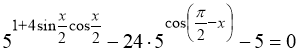 .
.
Розв’язання.
![]() ,
,
![]() .
.
Нехай ![]() ,
, ![]() ,
,
![]() ,
,
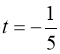 або
або ![]() .
.
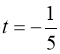 – сторонній корінь.
– сторонній корінь.
![]()
![]() ;
; 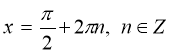 .
.
Відповідь: 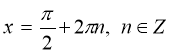 .
.
Варіант 9.
Завдання 4.2.
Розв’яжіть рівняння
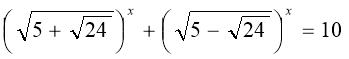 .
.
Розв’язання
Оскільки ![]() ,
,
то 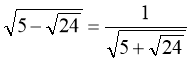 ,
,
тоді 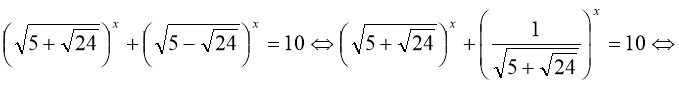
![]()
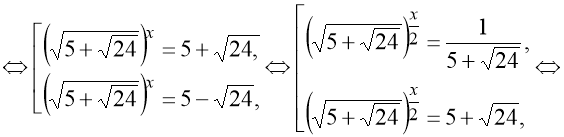
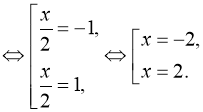
Відповідь: -2; 2.
Варіант 20.
Завдання 4.3.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
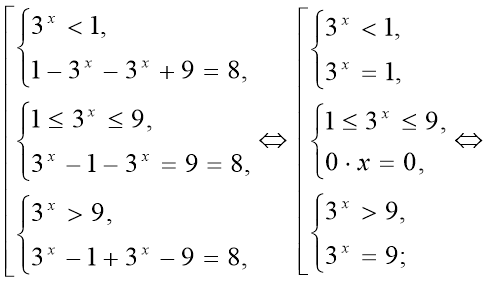
![]() .
.
Відповідь: ![]() .
.
Варіант 22.
Завдання 4.3.
![]() .
.
Розв’язання.
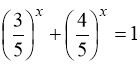 . Оскільки ліва частина рівняння представляє собою спадну функцію, а права – сталу , то рівняння має єдиний корінь
. Оскільки ліва частина рівняння представляє собою спадну функцію, а права – сталу , то рівняння має єдиний корінь ![]() , дійсно
, дійсно 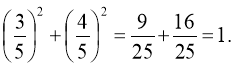
Доведемо, що інших розв’язків не має.
Кожна із функцій 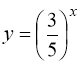 і
і 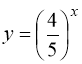 як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Тому, при
як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Тому, при ![]() ліва частина рівняння
ліва частина рівняння 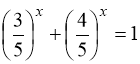 менша за одиницю, а при
менша за одиницю, а при ![]() - більша одиниці. Отже,
- більша одиниці. Отже, ![]() - єдиний розв’язок рівняння.
- єдиний розв’язок рівняння.
Відповідь: 2.
Варіант 29.
Завдання 4.1.
![]() .
.
Розв’язання.
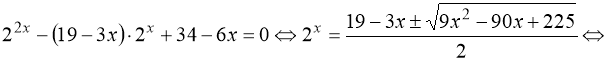
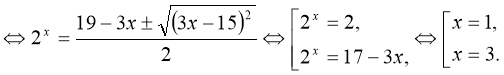
Рівняння ![]() має єдиний розв’язок, оскільки ліва частина рівняння
має єдиний розв’язок, оскільки ліва частина рівняння ![]() - зростаюча функція, а
- зростаюча функція, а ![]() - спадна функція, отже
- спадна функція, отже ![]() - єдиний розв’язок цього рівняння.
- єдиний розв’язок цього рівняння.
Відповідь: 1; 3.
Варіант 30.
Завдання 4.2.
При яких значеннях параметра а рівняння ![]() має два різних корені?
має два різних корені?
Розв’язання.
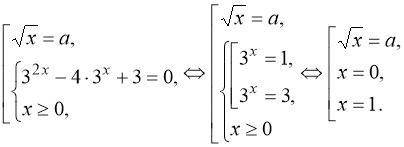
Рівняння має два різних корені при ![]() , або
, або ![]() .
.
Відповідь: Рівняння має два різних корені при ![]() , або
, або ![]() .
.
Варіант 38.
Завдання 4.1.
При яких значеннях параметра а рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання.
![]() ,
, 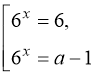 .
.
Рівняння має єдиний розв’язок, якщо ![]() , або
, або ![]() .
.
Відповідь: ![]() .
.
Варіант 33.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
![]() , якщо
, якщо ![]() , то
, то ![]()
![]() – розв’язків не має.
– розв’язків не має.
Якщо ![]() , то
, то ![]() .
.
Відповідь: -2.
Варіант 43.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Розглянемо функцію ![]() ,
, ![]() .
.
Ця функція має два проміжки монотонності: 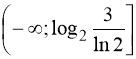 і
і  , на кожному з яких дана функція має не більше ніж один корінь
, на кожному з яких дана функція має не більше ніж один корінь ![]() ,
, ![]() .
.
Відповідь: 1; 3.
Варіант 48.
Завдання 4.3.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Виконаємо перетворення виразу ![]() , тоді маємо
, тоді маємо ![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
Прологарифмуємо обидві частини отриманого рівняння за основою 2:
![]() ,
, ![]()
![]() ,
, ![]()
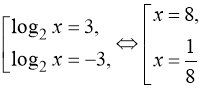 .
.
Відповідь: 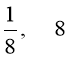 .
.
Варіант 51.
Завдання 4.1.
При яких значеннях параметра а рівняння ![]() має два дійсних різних корені? Розв’язання.
має два дійсних різних корені? Розв’язання.
![]()
![]()
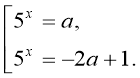
Рівняння має два різних дійсних корені, якщо
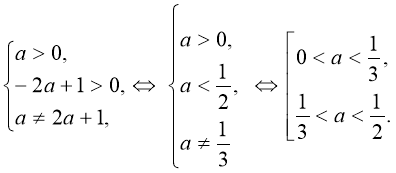
Відповідь: Рівняння має два різних дійсних корені при 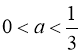 або при
або при 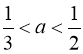 .
.
Варіант 54.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
![]()
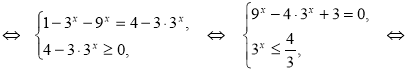
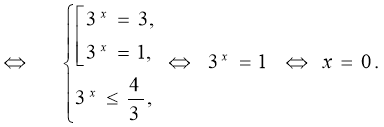
Відповідь: 0.
Варіант 55.
Завдання 4.1.
Розв’яжіть рівняння
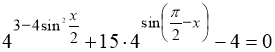 .
.
Розв’язання.
![]() ,
,
![]() ,
,
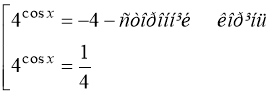
![]()
![]() ,
, ![]() .
.
Відповідь: ![]() ,
, ![]() .
.
Варіант 59.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Оскільки ![]() , то
, то 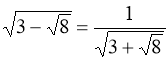 ,
,
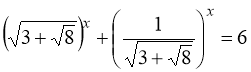 ,
,
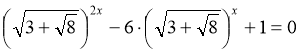 ,
,
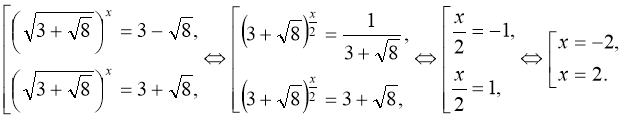
Відповідь: – 2; 2.
Варіант 70.
Завдання 4.3.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
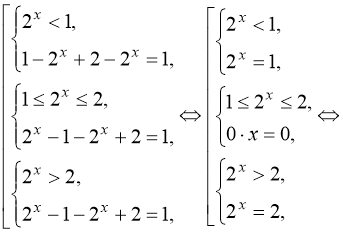
![]() .
.
Відповідь: ![]() .
.
Варіант 72.
Завдання 4.3.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
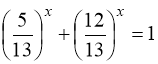 . Оскільки ліва частина рівняння спадна функція, а права – стала, тому рівняння має єдиний корінь
. Оскільки ліва частина рівняння спадна функція, а права – стала, тому рівняння має єдиний корінь ![]() , дійсно
, дійсно 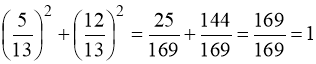 .
.
Доведемо, що інших розв’язків не має.
Кожна із функцій  і
і 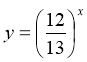 як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Тому, при
як показникова функція з основою, меншою за одиницю, є монотонно спадною. Сума цих функцій – також монотонно спадна функція. Тому, при ![]() ліва частина рівняння
ліва частина рівняння 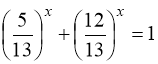 менша за одиницю, а при
менша за одиницю, а при ![]() - більша одиниці. Отже,
- більша одиниці. Отже, ![]() - єдиний розв’язок рівняння.
- єдиний розв’язок рівняння.
Відповідь: 2.
Варіант 79.
Завдання 4.1.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
![]() ,
,
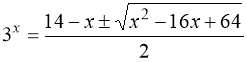 ,
,
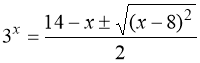 ,
,
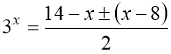 ,
,
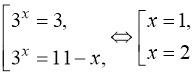 , тому що рівняння
, тому що рівняння ![]() має єдиний розв’язок, оскільки ліва частина рівняння – зростаюча функція, а права – спадна.
має єдиний розв’язок, оскільки ліва частина рівняння – зростаюча функція, а права – спадна.
Відповідь: 1; 2.
Варіант 80.
Завдання 4.2.
При яких значеннях параметра а рівняння ![]() має два різних корені?
має два різних корені?
Розв’язання.
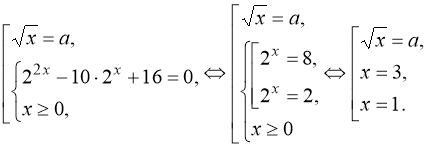
Рівняння має два різні корені якщо ![]() , або
, або ![]() , або
, або ![]() .
.
Відповідь: Рівняння має два різні корені якщо ![]() , або
, або ![]() , або
, або ![]() .
.
Варіант 83.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Якщо ![]() , то
, то ![]()
![]() - розв’язків не має.
- розв’язків не має.
Якщо ![]() , то
, то ![]()
![]()
![]()
![]()
![]() .
.
Відповідь: – 1.
Варіант 88.
Завдання 4.1.
При яких значеннях параметра а рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання.
![]()
![]()
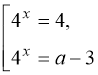 .
.
Рівняння має єдиний розв’язок, якщо ![]()
![]()
![]() , або
, або ![]()
![]()
![]() .
.
Відповідь: ![]() .
.
Варіант 94.
Завдання 4.2.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Розглянемо функцію ![]() ,
, ![]() .
.
Ця функція має одну точку екстремуму 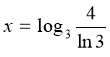 і два інтервали монотонності, отже ця функція має не більше за два нулі, тому
і два інтервали монотонності, отже ця функція має не більше за два нулі, тому ![]() і
і ![]() - корені даного рівняння.
- корені даного рівняння.
Відповідь: 0; 2.
Варіант 98.
Завдання 4.3.
Розв’яжіть рівняння
![]() .
.
Розв’язання.
Оскільки 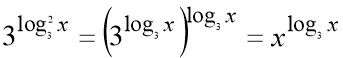 , то
, то
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
Логарифмуємо обидві частини отриманого рівняння за основою 3:
![]() ,
, ![]()
![]() ,
, ![]()
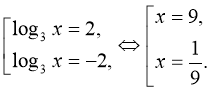
Відповідь: 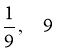 .
.
V. Варіанти індивідуальних завдань
Завдання 1.
Розв’язати рівняння.
1. 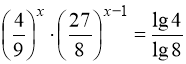 . 2.
. 2. ![]() .
.
3. 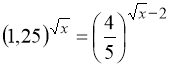 . 4.
. 4. 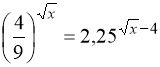 .
.
5. 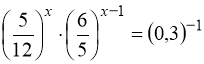 . 6.
. 6. 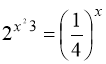 .
.
7. ![]() . 8.
. 8. ![]() .
.
9. ![]() . 10.
. 10. ![]() .
.
Завдання 2.
Розв’язати рівняння.
1. ![]() . 2.
. 2. 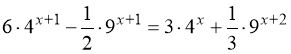
3. ![]() . 4.
. 4. ![]() .
.
5. 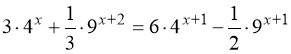 .
.
6. ![]() .
.
7. ![]() .
.
8. ![]() .
.
9. ![]() .
.
10. ![]() .
.
Завдання 3.
Розв’язати рівняння.
1. ![]() . 2.
. 2. ![]() .
.
3. 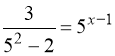 . 4.
. 4. ![]() .
.
5. ![]() . 6.
. 6. ![]() .
.
7. ![]() . 8.
. 8. ![]() .
.
9. ![]() . 10.
. 10. ![]() .
.
Завдання 4.
Розв’язати рівняння.
1. ![]() . 2.
. 2. 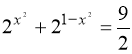 .
.
3. 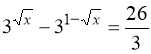 . 4.
. 4. ![]() .
.
5. 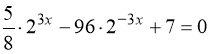 . 6.
. 6. ![]() .
.
7. ![]() . 8.
. 8. ![]() .
.
9. ![]() . 10.
. 10. 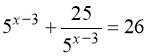 .
.
Завдання 5.
Розв’язати рівняння.
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() .
.
5. ![]() . 6.
. 6. ![]() .
.
7. ![]() . 8.
. 8. ![]() .
.
9. ![]() . 10.
. 10. ![]() .
.
Завдання 6.
Розв’язати рівняння.
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() .
.
5. ![]() . 6.
. 6. ![]() .
.
7. ![]() . 8.
. 8. ![]() .
.
9. ![]() . 10.
. 10. ![]()
Завдання 7.
Розв’язати рівняння.
1. ![]() . 2.
. 2. ![]() .
.
3. ![]() . 4.
. 4. ![]() .
.
5. ![]() . 6.
. 6. ![]() .
.
7. ![]() . 8.
. 8. ![]() .
.
9. 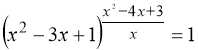 . 10.
. 10. ![]() .
.
VІ. Вправи для самостійної роботи
1. Обчислити: 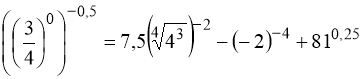 .
.
2. Нескінченні періодичні дроби перетворити у звичайні:
а) 1,2727…; б) 0,34545… .
3. Спростити:
а) 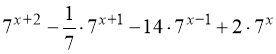 ;
;
б) 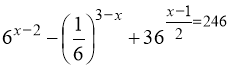 ;
;
в) 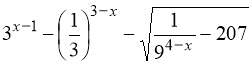 ;
;
г) ![]() .
.
4. 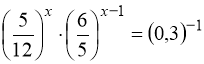 .
.
5. 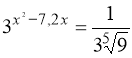 .
.
6. 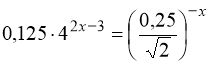 .
.
7. ![]() .
.
8. 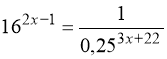 .
.
9. 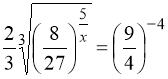 .
.
10. ![]() .
.
11. 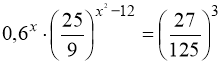 .
.
12. 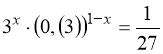 .
.
13. ![]() .
.
14. 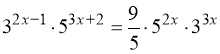 .
.
15. ![]() .
.
16. 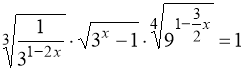 .
.
17. ![]() .
.
18. 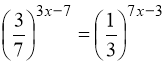 .
.
19. ![]() .
.
20. ![]() .
.
21. ![]() .
.
22. ![]() .
.
23. ![]() .
.
24. ![]() .
.
25. 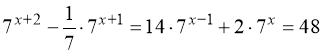 .
.
26. ![]() .
.
27. ![]() .
.
28. ![]() .
.
29. ![]() .
.
30. 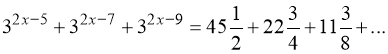 .
.
31. ![]() .
.
32. ![]() .
.
33. ![]() .
.
34. ![]() .
.
35. ![]() .
.
36. ![]() .
.
37. ![]() .
.
38. ![]() .
.
39. ![]() .
.
40. 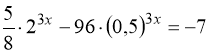 .
.
41. ![]() .
.
42. ![]() .
.
43. ![]() .
.
44. 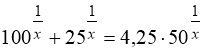 .
.
45. ![]() .
.
46. ![]() .
.
47. ![]() .
.
48. ![]() .
.
49. ![]() .
.
50. ![]() .
.
51. ![]() .
.
52. ![]() .
.
53. ![]() .
.
54. ![]() .
.
55. ![]() .
.
56. ![]() .
.
57. ![]() .
.
58. ![]() .
.
59. ![]() .
.
60. ![]() .
.
61. ![]() .
.
62. ![]() .
.
63. ![]() .
.
64. ![]() .
.
65. На множині додатних чисел розв’язки рівняння ![]() .
.
Відповіді та вказівки
1. 3.
2. а) ![]() ; б)
; б) ![]() .
.
3. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4. – 2.
5. 0,2; 7.
6. 6.
7. 152.
8. 24.
9. ![]() .
.
10. 1,5.
11. – 2,5; 3. Вказівка: 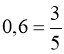 ;
; 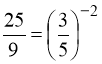 ;
;  .
.
12. – 1. Вказівка: 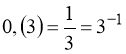 ;
; 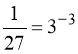 .
.
13. 10; 30. Вказівка: 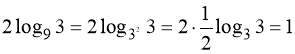 .
.
14. –3. Вказівка: ![]() ;
; 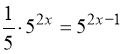 . Тоді:
. Тоді: 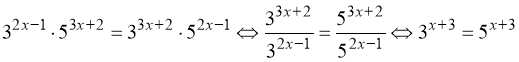 .
.
15. 0,5. Вказівка: ![]() . Тоді:
. Тоді: 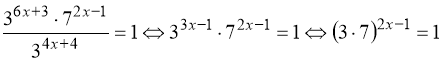 .
.
16. 0,8.
17. 3. Вказівка: ![]() . Тоді:
. Тоді: 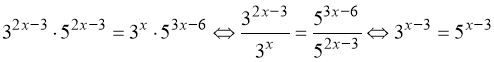 .
.
18. 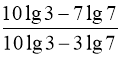 . Вказівка: прологарифмувати обидві частини за основою 10:
. Вказівка: прологарифмувати обидві частини за основою 10:
![]()
![]() .
.
19. 3; ![]() . Вказівка: прологарифмувати обидві частини за основою 3. Враховувати, що
. Вказівка: прологарифмувати обидві частини за основою 3. Враховувати, що ![]() . Записуючи відповідь перетворити:
. Записуючи відповідь перетворити: 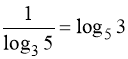 .
.
20. – 1. Вказівка: ![]()
![]()
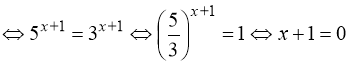 .
.
21. 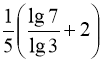 .
.
22. 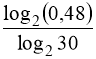 . Вказівка: прологарифмувати обидві частини за основою 2. Див. приклад 20.
. Вказівка: прологарифмувати обидві частини за основою 2. Див. приклад 20.
23. ![]() ; 2. Вказівка: Впізнати, що х = 2 – один з розв’язків рівняння, прологарифмувати обидві частини за основою 3; перетворити у вигляд:
; 2. Вказівка: Впізнати, що х = 2 – один з розв’язків рівняння, прологарифмувати обидві частини за основою 3; перетворити у вигляд: ![]() .
.
Далі – див. приклад 21.
24. 12. Вказівка: ![]()
![]() .
.
25. 0. Вказівка: Винести за дужки ![]() . Див. приклад 22.
. Див. приклад 22.
26. 4. Вказівка: Див. приклад 23.
27. 68. Вказівка: 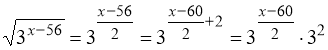 . Тоді:
. Тоді:
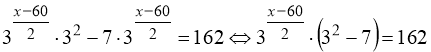 .
.
28. 2,5. Вказівка. Див. приклад 25.
29. ![]() ;
; ![]() . Вказівка: Див. приклад 25.
. Вказівка: Див. приклад 25.
30. 4,5. Вказівка. У правій частині – нескінченно спадна геометрична прогресія. 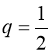 ;
; ![]() . Далі – див. приклад 26.
. Далі – див. приклад 26.
31. 2. Вказівка: ![]() . Далі – див. приклад 27.
. Далі – див. приклад 27.
32. 1. Вказівка: 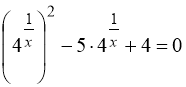 ;
; 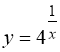 .
.
33. ![]() ; – 1; 1;
; – 1; 1; ![]() . Вказівка:
. Вказівка: ![]() ;
; ![]() .
.
34. 20. Вказівка:
![]() ; .
; . 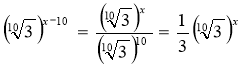
Заміна: ![]() . Тоді:
. Тоді: 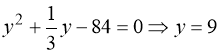 .
.
35. 1,5. Вказівка: ![]() ;
; 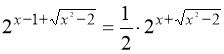 . Заміна:
. Заміна: ![]() .
.
Тоді: ![]()
![]()
![]() .
.
36. 2. Вказівка: ![]() ;
; ![]() .
.
Заміна: ![]() .
.
37. 25. Вказівка: ![]() ;
; ![]() ;
; 
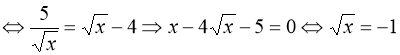 або
або ![]() . Корінь
. Корінь ![]() - сторонній. Див. приклад 28.
- сторонній. Див. приклад 28.
38. 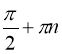 ,
, ![]() . Вказівка:
. Вказівка: ![]() ;
; 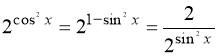 .
.
Заміна: ![]() . Тоді:
. Тоді:  або
або ![]() ;
;
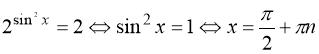 ,
, ![]() ;
;
![]() Ø.
Ø.
39. 4. Вказівка: ![]() . Див. приклад 30.
. Див. приклад 30.
40. 1. Вказівка: 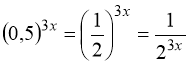 . Заміна:
. Заміна: ![]() .
.
Див. приклад 31.
41. – 1; 2. Вказівка: 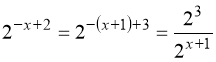 . Заміна:
. Заміна: ![]() .
.
Див. перетворення виразу 69.
42. – 2; 2. Вказівка: Примітимо, що ![]() .
.
Заміна: ![]() ;
; 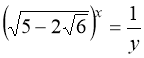 . Тоді:
. Тоді: 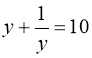 .
.
Див. приклад 32.
43. 0; 1. Вказівка: Почленно розділити на 9х ![]() 0. Заміна:
0. Заміна: 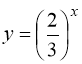 .
.
Див. приклад 34.
44. – 0,5; 0,5. Вказівка: Почленно розділити на ![]() ,
, 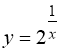 .
.
Див. приклад 33.
45. 2. Вказівка: Почленно розділити на ![]() . Заміна:
. Заміна: 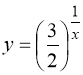 . Див. приклад 34, 28.
. Див. приклад 34, 28.
46. – 1. Вказівка: ![]() . Почленно розділити на
. Почленно розділити на ![]() . Заміна:
. Заміна: 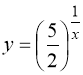 .
.
47. ![]() ; 2;
; 2; ![]() ; 0. Вказівка: Почленно розділити на
; 0. Вказівка: Почленно розділити на ![]() . Заміна:
. Заміна: 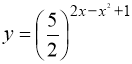 . Див. приклад 35.
. Див. приклад 35.
48. 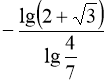 ;
; 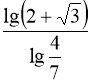 ; 0. Вказівка: Обі частини розділити на
; 0. Вказівка: Обі частини розділити на ![]() . Заміна:
. Заміна: 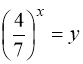 . Тоді:
. Тоді: ![]()
![]() . Далі – див. приклад 37. Врахувати, що
. Далі – див. приклад 37. Врахувати, що 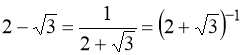 ;
; ![]() .
.
49. Ø. Вказівка: Див. приклад 38.
50. – 1; 1. Вказівка: Див. приклад 38.
51. 1. Вказівка: Очевидний розв’язок ![]() . Поділимо обидві частини рівняння на
. Поділимо обидві частини рівняння на ![]() :
: 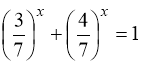 . Доведення єдиності кореня
. Доведення єдиності кореня ![]() - Див. приклад 39.
- Див. приклад 39.
52. ![]() . Вказівка: Привести до вигляду:
. Вказівка: Привести до вигляду: 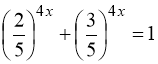 . Очевидний розв’язок:
. Очевидний розв’язок: 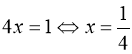 , він єдиний – Див. приклад 39.
, він єдиний – Див. приклад 39.
53. 1. Вказівка: Очевидний розв’язок ![]() . Довести, що інших розв’язків не має. Див. приклад 40.
. Довести, що інших розв’язків не має. Див. приклад 40.
54. 2; 4; 5; 6. Вказівка: Розглянути 4 випадки (див. приклад 41).
1) ![]() ;
;
2) ![]() - сторонній корінь, так як при
- сторонній корінь, так як при ![]() ;
; ![]() і
і ![]() ;
;
3) ![]() ;
;
4) ![]() або
або ![]() .
.
55. – 5; – 4; – 2. Вказівка: Розглянути 4 випадки (див. приклад 41):
1) ![]() ;
;
2) ![]() ; - сторонній корінь;
; - сторонній корінь;
3) ![]() ; - сторонній корінь;
; - сторонній корінь;
4) ![]() або
або ![]() .
.
56. – 2; 3; 5. Вказівка: Розглянути 3 випадки (див. приклад 42):
1) ![]() ;
;
2) ![]() ;
;
3) ![]() або
або ![]() .
.
57. ![]() .
.
58. ![]() . Вказівка: Зробимо заміну
. Вказівка: Зробимо заміну ![]() . Тоді:
. Тоді: ![]() .
.
59. 2. Вказівка: ![]() .
.
60. 2. 61. ![]() . 62.
. 62. ![]() . 63.
. 63. ![]() . 64. 4. 65.
. 64. 4. 65. ![]() .
.
Література
- Бородуля И.Т. Показательные и логарифмические уравнения и неравенства. – М.: Просвещение, 1968 – 112с
- Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И., Задачи по математике. Уравнения и неравенства: Справочное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 240с.
- Збірник задач з математики для вступників до ВТУЗів. / за ред. М.І. Сканаві. – 3-тє вид. стер. –К.: Вища шк.., 1996. – 445с.
- Чудутов Ю.В. Показникові рівняння. КООГУ.-К., 1996-60с.
- Яремчик Ф.П., Ясінський В.В. Показникові та логарифмічна функції. Програма. Типові задачі. / НТУУ «КПІ». – К., 1997.- 29с.
- Ясінський В.В. Вибрані конкурсні задачі з математики. / КПІ. – К., 1992. – 62с.
- Ясінський В.В., Барановська Г.Г. Практикум з математики. Показникова та логарифмічна функції. Навч. Посібник / за ред.. В. В. Ясінського. – К.: «КПІ», 1998. – 124с.
1


про публікацію авторської розробки
Додати розробку

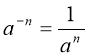 (
(