Методичний посібник "Різні способи доведення теореми Піфагора"

 

Турчин С. О.

 

 

Зміст

Вступ

Розділ І. Історична довідка

1.      Піфагор і його теорема.
2.      Єгипетський трикутник.
3.      Китайське правило «Гоу – гу».
4.      Індійська теорема.

Розділ ІІ. Формулювання теореми Піфагора.

Сатиричне зображення теореми Піфагора.

Розділ ІІІ. Доведення теореми Піфагора.

3.1. Доведення за означенням косинуса.

3.2. Доведення методом координат.

3.3. Векторний метод доведення.

3.4. Доведення за подібністю трикутників.

3.5. Доведення за теоремою косинусів.

3.6. Доведення з використанням основної тригонометричної тотожності.

3.7.Доведення з використанням властивості січної та дотичної, проведених до кола з однієї точки.

3.8. Доведення з використанням формули площі трапеції.

3.9. Доведення з використанням формул площ трикутників.

3.10. Доведення з використанням теореми Птоломея.

3.11. Доведення з використанням теореми про суму квадратів діагоналей.

3.12. Доведення Кушніра.

3.13. Доведення з використанням формули бісектриси.

3.14. Доведення за формулою Архімеда.

3.15. Доведення Евкліда.

3.16. Доведення Насіреддіна.

3.17. Доведення Гофмана.

3.18. Доведення Темпельгофа.

3.19. Доведення Ренана.

3.20. Давньоіндійське доведення Бхаскара.

3.21. Давньокитайське доведення.

3.22. Доведення за малюнком.

3.23. Доведення зважуванням.

3.24. Доведення розрізанням та перекроюванням.

Висновки

Література

 

Вступ

                                                                   Світ, що нас оточує, -

це світ геометрії.

То ж давайте його пізнавати!

Почувши ім’я Піфагора, ми відразу пригадуємо знамениту теорему: «У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гіпотенузи». Теорема Піфагора чудова тим, що сама по собі вона зовсім не очевидна. Скільки не дивися на прямокутний трикутник, ніяк не побачиш, що між його сторонами є таке просте співвідношення:

с² = а² + в². Але  це співвідношення стає очевидним, якщо вдало побудувати малюнок. У цьому є найкращий геометричний стиль: за допомогою правильної побудови зробити неочевидне очевидним. У математичних трактатах Древньої Індії, доводячи теорему, часто наводили тільки малюнок. Супроводжували його лише одним словом: «Дивись!»

Теорема допускає багато красивих доведень. Це доведення за подібністю трикутників, методом координат, векторним методом, у вигляді малюнків  і, навіть, зважуванням. Американський любитель математики Е. Луміс зібрав 367 різних доведень теореми Піфагора, і колекція їх поповнюється і далі.

Відкриття цієї теореми мало вирішальний вплив на подальший розвиток античної  математики, бо це привело до встановлення існування несумірних відрізків у геометрії та ірраціональних чисел у алгебрі.

Дана робота про різні доведення теореми Піфагора. Цю теорему доводили Евклід, Бхаскара, Насіреддін, Ренан, Гофман та інші. Ми також довели теорему Піфагора  використавши теорему косинусів.

Розділ І. Історична довідка

1.   Піфагор і його теорема.

Легендою і джерелом дискусій Піфагор став в стародавні часи. У 306 році до н. е. йому, як найрозумнішому з греків, поставили пам’ятник у римському форумі.

Піфагор багато подорожував. Він здійснив традиційну подорож до Єгипту, де жив близько 22 років і витримав немало випробувань, перш ніж жерці відкрили йому «хитромудрі правила геометрії». До вавілонських магів і халдеїв він потрапив проти своєї волі і прожив 12 років, вивчив їхні релігійні таїнства та математику. Побував він у Індії, де спілкувався з брахманами. Тому тепер важко визначити, що зробив він сам, а що запозичив у інших.

Найбільшу славу Піфагору принесла відкрита ним «теорема Піфагора», яка і до цього часу вважається однією з найважливіших теорем геометрії.

Доведення самого Піфагора своєї знаменитої теореми до нас не дійшло. У всякому разі, залежність між сторонами прямокутного трикутника була відома ще за 1500 років до його народження в Древньому Вавилоні та Єгипті. Отже, Піфагор не знайшов цю властивість прямокутних трикутників – він тільки першим зміг узагальнити і довести її, перевести її з практики в галузь науки. Як він це зробив, невідомо.

Частинні випадки теореми Піфагора були відомі деяким давнім народам до Піфагора.

1.2. Єгипетський трикутник.

        В своїй будівельній практиці єгиптяни користувалися так званим «єгипетським трикутником» із сторонами 3, 4 і 5. Вони знали, що вказаний трикутник є прямокутним і для нього виконується співвідношення 3² + 4² = 5². Для побудови прямого кута користувались таким способом: мотузок ділили вузлами на 12 рівних частин і кінці зв’язували. Потім його розтягували на землі так, щоб утворився трикутник із сторонами 3, 4 і 5 поділок. Кут трикутника протилежний до                 сторони, яка має 5 поділок, був прямий. Можна припустити, що цей трикутник став відомим Піфагору після подорожі по Єгипту і Вавилону.

1.3. Китайське правило «Гоу – гу».

У стародавньому Китаї теорему Піфагора застосовували біля 2200 років до нашої ери. В  знаменитому трактаті «Математика в дев’яти книгах» теорема про співвідношення сторін у прямокутному трикутнику використовувалась під виглядом правила «Гоу – гу». Згідно цьому правилу, китайці по відомій гіпотенузі і одному катету знаходили інший, невідомий катет, а також гіпотенузу, якщо було відомо обидва катети.

Терміни «гоу» і «гу» позначають катети прямокутного трикутника, де «гоу» - горизонтальний, менший катет, а «гу» - вертикальний, більший катет («гоу» - крюк, «гу» - ребро, зв’язка).

1.4 Індійська теорема.

Індійським вченим теорема Піфагора стала відома не пізніше VІІІ ст. до н. е. В найстарішій пам’ятці індійської геометрії «Сулва – сутрах» ця теорема формулювалася так: «Веревка, проведенная наискось в продольном квадрате (прямоугольнике), образует то же, что образует вместе каждая из мер: продольных и поперечних» або «То, что образуется на двух сторонах, равно тому, что образуется по диагонали».

Розділ ІІ. Формулювання теореми Піфагора.

 1.У прямокутному трикутнику сума квадратів катетів дорівнює    квадрату гіпотенузи.

     2. Сума площ квадратів, побудованих на двох катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на його гіпотенузі.

     3. Якщо трикутник прямокутний, то сума площ квадратів, побудованих  на обох катетах, дорівнює квадрату, побудованому на гіпотенузі.

     4. Площа квадрата, побудованого на катеті, дорівнює площі прямокутника, побудованого на гіпотенузі і на проекції цього катета на гіпотенузу.

5. Класичне формулювання теореми.

Якщо сторони прямокутного трикутника є сторонами квадратів, то площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах.

Сатиричне зображення теореми Піфагора

                            

 

                        

Розділ ІІІ. Різні способи доведення теореми Піфагора

3.1. Доведення за означенням косинуса.

Проведемо висоту СD  з вершини прямого кута С. За означенням косинуса кута

;     ;  .

       ;     ;  .

Додамо почленно рівності, дістанемо:

.

Отже, .

3.2.  Доведення методом координат.

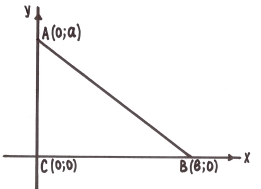
Введемо систему координат: катети трикутника лежать на осях, початок координат у вершині прямого кута.

Тоді А (0; а), В (в; 0), С (0; 0). Знайдемо відстані АВ, АС, ВС.

АВ² = (0 – в)² + (а – 0)² = в² + а²,

АС² = (0 – 0)² + (а – 0)² = а²,

ВС² = (в – 0)² + (0 – 0)² = в².

Звідси  АВ² = АС² + ВС².

3.3. Векторний метод доведення.

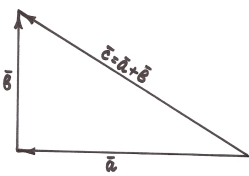
Нехай (а_х, а_у),   (в_х, в_у), (а_х + в_х, а_у + в_у,), тобто = + . 

∙= а_х в_{х +} а_у в_у.    Оскільки  , то.

ā² = а_х² + а_у²;  = в_х² + в_у²;  = (а_х + в_х)² + (а_у + в_у)².

= а_х²+2 а_х в_х+в_х²+а_у²+2 а_у в_у+в_у²=(а_х²+а_у²)+(в_х²+в_у²)+2(а_х в_{х +} а_у в_у) =

 ā²++2 · ā · = ā² + + 0.     Отже, с² = а² + в².

3.4. Доведення за подібністю трикутників.

 Проведемо висоту СD на гіпотенузу АВ.  Маємо подібні трикутники:

АВС ~ АСD ~ ВСD (внаслідок рівності кутів).

Складаємо пропорції:   ;  ;

                                        ;  

Додамо почленно рівності:

АС² + ВС² = АВ · АD + АВ · ВD =АВ ∙ (АD + ВD) = АВ · АВ = АВ²

3.5. Доведення за теоремою косинусів.

      За теоремою косинусів АВ² = АС² + ВС² – 2 АС ∙ ВС ∙ cos С

      Оскільки, cos С = cos 90° = 0, то АВ² = АС² + ВС²  або с² = в² + а².

3. 6. Доведення з використанням

основної тригонометричної тотожності.

Відомо, що , , звідки маємо:, . В обох рівностях піднесемо обидві частини до квадрата, отримаємо: , . Додамо почленно ці рівності: ,   . Звідси, .

3. 7. Доведення з використанням властивості січної та дотичної, проведених до кола з однієї точки.

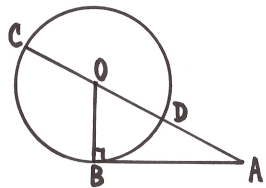
Будуємо коло з центром у точці О і радіусом ОВ. Воно перетне гіпотенузу АО в точці D. Оскільки АВ ОВ, де ОВ – радіус, то це означає, що АВ – дотична до кола. Пряма АО є січною і перетинає коло в точках D і С. За властивістю січної і дотичної, проведених до кола з однієї точки, маємо: . Оскільки , ,то . Підставляємо знайдені вирази у формулу: , ,  .

3.8. Доведення з використанням формули площі трапеції.

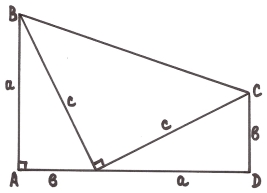
 прямокутна трапеція з основою та ; висота трапеції. За формулою площі трапеції маємо: .

З іншого боку, трапеція складається з прямокутних трикутників . Тому її площа дорівнює сумі площ цих трикутників, тобто . Відомо, що площа прямокутного трикутника дорівнює половині добутку катетів. Отже: . Тоді . Прирівняємо праві частини рівностей: .

3. 9. Доведення з використанням формул  площ трикутників.

Впишемо в ∆АВС (С=90˚) коло з центром у точці О. Відомо, що . З іншого боку , де  - півпериметр ∆АВС, - радіус вписаного в прямокутний трикутник кола. З двох рівностей для площі ∆АВС маємо:

3. 10. Доведення з використанням теореми Птоломея.

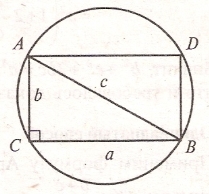
Скористаємось теоремою Птоломея:   .

3. 11. Доведення з використанням теореми

про суму квадратів діагоналей.

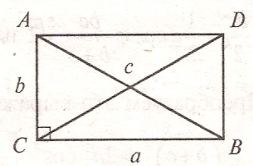
Доповнимо прямокутний трикутник до прямокутника і скористаємося теоремою про суму квадратів діагоналей.

або .

3. 12. Доведення Кушніра.

Позначимо - кут між бісектрисою і висотою АН₁ . Застосуємо авторську формулу (Тріумф шкільної геометрії: Навчальний посібник для 7 – 11 класів – К. : Наш час, 2005) . Для прямокутного ∆АВС (А=90˚) . Нехай для визначеності В >С. Тоді , (з ∆).

Маємо: або  .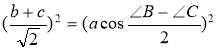

Перетворимо цей вираз:

Значить, .

3. 13.  Доведення з використанням формули бісектриси.

                        

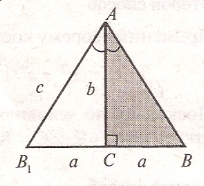
Скористаємося формулою бісектриси . Маємо ∆АВС (С=90˚). Виконаємо осьову симетрію відносно катета АС. Одержимо рівнобедрений ∆АВВ₁ з бісектрисою АС = . Маємо:

АС²=АВ∙АВ₁-ВС∙СВ₁ або .

3.14. Доведення за формулою Архімеда.

Застосуємо формулу Архімеда: (К – проекція точки В на сторону АС). Доведення зводиться до способу 3.12.: ∆ - прямокутний, рівнобедрений. . Оскільки , то 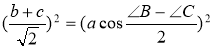. Далі доведення аналогічне попередньому.

3. 15. Доведення Евкліда.

                

 

                         

 

                      

 

 

              

 

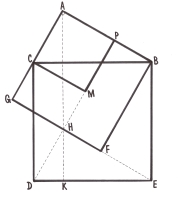
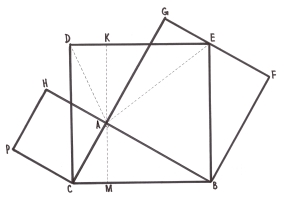
Пропонуємо одне з доведень Евкліда

Нехай АВС – прямокутний трикутник ( ВАС= 90˚). Побудуємо квадрати    BCDE AMNC ABPT. Проведемо AL BC . Доведемо, що прямокутник BKLE рівновеликий квадрату BPTA, а прямокутник KCDL – квадрату AMNC.

Проведемо відрізки PC і AE. площа ∆PCB рівна половині площі квадрата BPTA. Площа ∆ABE рівна половині площі прямокутника BKLE. ∆ABE=∆PBC.  Звідси  випливає, що прямокутник  BKLE рівновеликий квадрату BPTA. З’єднавши N з B і A з D, аналогічно доведемо, що прямокутник KCDL рівновеликий квадрату AMNC. Звідси випливає, що квадрат BCDE рівновеликий сумі площ квадратів PTAB і AMNC.

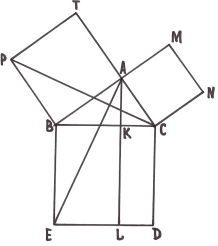
3.16. Доведення Насіреддіна.

GAL = ABC, LA = CB, GAL = ABC = CAM,

Тому точки L, А, М, К лежать на одній прямій.

Отримали фігури з рівними площами:

S_DKMC = S_CALD = S_CAНP = в².

Аналогічно:       S_KEBM =     S_ABEL = S_ABFG = c²

Але  S_DEBC = S_DKMC + S_KEBM = a². Отже, a² = в² + c².

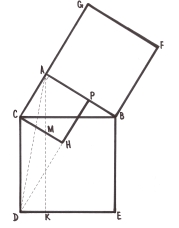
3.17. Доведення Гофмана 1.

 

 Проведемо BF    АВ,   BF = АВ,СР    СА,   СР = СА,

ВЕ    ВС,   ВЕ = ВС. Доводимо, що точки  F, А і Р лежать на одній прямій. Чотирикутники РFВС і АВЕС рівновеликі, оскільки СВF = АВF і S_PCE = S_ACE. Віднявши від обох чотирикутників площу спільного АВС, матимемо: . Тобто a² = в² + c².

Доведення Гофмана 2.

 

Продовжимо відрізок CD до перетину з продовженням відрізка

FL у точці N. Отримаємо фігури з рівними площинами:

S_PALN = S_CALD = S_CAHI = в², S_ABEL = S_ABFG = c²,

S_PBEN = S_CBED  = a². Але S_PBEN = S_PALN + S_ABEL

Отже,  a² = в² + c².

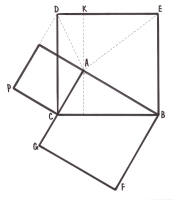
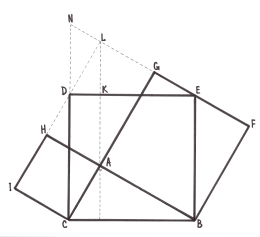
3.18. Доведення Темпельгофа.

LDE = ABC,  AGH = ABC.

Рівними будуть чотирикутники LDCA, FBCP i ABEL та PHGF i PCBE.

Отже, шестикутники РСВFGН  і АСDLEB  рівноскладені.

Вони мають спільний ABC, а також AGH = LDE.

Це означає, що S_CDEB = S_CAHP + S_ABFC  або a² = в² + c².

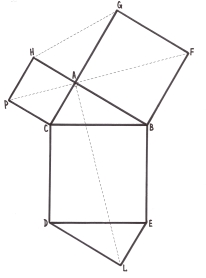
3.19. Доведення Ренана.

 

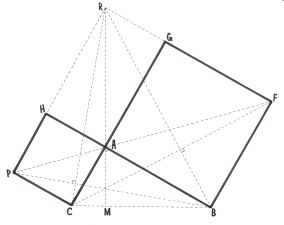
Оскільки НRA = АВС, то RА = ВС.

З рівностей РВС = САR, FВС = ВАR

випливає, що RA    ВС, РВ   СR і СF   ВR.

RA, ВР і СF є висотами ВСR, тому вони перетинаються в одній точці.

, ,

тому 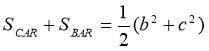 . Але ,   .

Тому .

Отже, a² = в² + c².

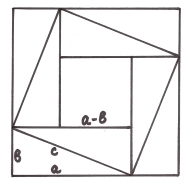
3.20. Давньоіндійське доведення  математика Бхаскари

в книзі «Вінок знань» (біля 1150р.).

Доведення теореми дається у вигляді малюнка з надписом «Дивись!»

Площа квадрата, побудованого на гіпотенузі с трикутника, рівновелика сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого а – в.

. Звідки,  с² = а² + в².

3.21. Давньокитайське доведення.

(а + в)² = 4ав + (а – в)² = 4· + с²,

тому  а² + 2ав + в² = 2ав + с²        а² + в²= с²

3.22. Доведення за малюнком.

                     

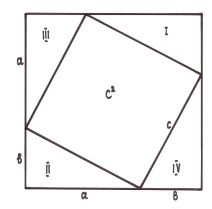
3.23. Доведення зважуванням.

Якщо вирізати з картону три квадрати, сторони яких дорівнюють сторонам даного трикутника і покласти два менших квадрати на одну шальку досить чутливих терезів, а на другу – третій квадрат, то терези будуть у рівновазі.

3.24. Доведення розрізанням та перекроюванням.

                                  

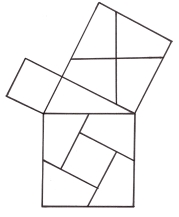
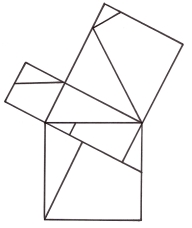
Висновки

Ми розглянули різні способи доведення теореми Піфагора. Зокрема доведення Евкліда, Бхаскара, Насіреддіна, Ренана, Гофмана, давньокитайське доведення, доведення за малюнком, доведення розрізанням і перекроюванням, доведення зважуванням.

Кожний спосіб по-своєму оригінальний. Ми показали, що дану теорему можна довести, використовуючи різні теореми, означення, формули. У 8 класі після вивчення означення косинуса – доводимо теорему за допомогою цього означення; після вивчення декартових координат – методом координат, після вивчення векторів – векторним методом. У 9 класі вивчаємо подібність трикутників – доводимо теорему за подібністю трикутників. Вивчили теорему косинусів і маємо новий спосіб доведення.

Література

 

1. Газета «Математика» № 45, 2004.
2. Гейзер Г. И. История математики в школе. – Москва: Просвещение, 1981.
3. Журнал «Математика в школах України» № 2, 2005.
4. Коба В. І., Хмура О.О. Позакласна робота з математики в школа. – Київ: Радянська школа, 1968.
5. Конфорович А.Г. Колумби математики. – Київ: Радянська школа, 1982.
6. Погорєлов О.В. геометрія: Підручник для 7 – 9 класів. – Київ: освіта, 2001.
7. Скобелєв Г.М., Берман П.В. Математика в позаурочний час. – Київ: радянська школа, 1973.
8. Смогоржевський О.С. Математична хрестоматія для 6 – 8 класів. – Київ: радянська школа, 1968.
9. Чистяков В.Д. Рассказы о математиках. – Минск: Вышейшая школа, 1966.
10. Шустеф Ф.М. Материал для внеклассной работы по математике. – Минск: Народная асвета, 1968.