Методика конструювання та приклади завдань з математики у форматі тестування PISA

 

Відділ освіти Тальнівської райдержадміністрації

Тальнівський районний методичний кабінет

Тальнівський економіко-математичний ліцей

 

Розділ виставки. Програмно-цільове та навчально-методичне забезпечення сучасного освітнього процесу.

 

 

 

Cкоропад Анна Сергіївна,

учитель математики

Методика конструювання та

приклади завдань з математики

у форматі тестування PISA

(Методичний посібник)

 

 

ЗМІСТ

 

Вступ

Розділ 1. Тестові технології в навчанні

1.1 Основні визначення

1.2 Конструювання тестів по формуванню функціональної математичної грамотності учнів

1.3 Міжнародна програма оцінки учбових досягнень учнів PISA

Розділ 2. Особливості тестових завдань по програмі PISA............10

2.1 Методика конструювання тестових завдань по математиці в контексті міжнародної програми PISA              10

2.2 Класифікація завдань

2.3 Компетентнісний підхід в освіті

Розділ 3. Приклади практико-орієнтованих завдань у форматі тестових завдань PISA

3.1 Приклади тестових завдань з програми PISA за рівнем компетентності та їх комплексний аналіз

3.2 Приклади практико-орієнтовних завдань в форматі PISA та їх аналіз

3.3 Завдання, що відповідають шкільній програмі 5-9 класів   та їх розв’язання………………………………………………………………………

3.4. Порівняльний аналіз тестування ЗНО і PISA……………………………..23

Розділ 4. Банк математичних завдань та їх класифікація…………………..26

Висновки..............................................59

Список використаних джерел.................................60

Вступ

 

Програму міжнародного оцінювання учнів PISA було започатковано в 1997 році Організацією з економічного співробітництва та розвитку (OECР).

Метою програми є визначення тенденцій у результатах освітніх програм різних країн; чинників, що впливають на рівень навчальних досягнень учнів у світі.

2018 року Україна вперше візьме участь у Програмі. Дослідження проводиться раз на три роки й спрямоване на оцінювання систем освіти в різних країнах світу на підставі тестування 15-річних учнів. Україна долучається до більш ніж 80-ти країн, що беруть участь у PISA – 2018.

Тому сьогодні є актуальним знайомство з цією програмою, методикою  конструювання та зокрема з завданнями з однієї з предметних галузей, яка входить до неї – математики.

 

Розділ 1. Тестові технології в навчанні

 

1.              Основні визначення

Тест – це:

- проба, випробування, дослідження;

- інструмент, який складається із завдання на діяльність цього рівня, що дозволяє виявити факт засвоєння;

- стандартизований метод діагностики рівня і структури підготовленості;

- система спеціально складених завдань, розв’язання яких має однозначно правильні відповіді;

- метод педагогічної діагностики.

Нині в освітній системі багатьох країн широко використовуються тестові форми навчання і контролю. Тестові технології більш економічні і оперативні як при навчанні, так і при проведенні випробувань, при обробці їх результатів.

В основному при цьому використовуються тести досягнень, які конструюються в основному на навчальному матеріалі і призначаються для визначення загальної підготовки по конкретних предметах, інакше кажучи, тести досягнення дають можливість озирнутися назад і встановити яким набором знань і умінь володіє учень, який проходить тест.

Проте, в практиці західних країн давно знайшли успішне застосування також тести здібностей, які дають можливість заглянути вперед і оцінити здатність учнів застосовувати отримані знання з практики.
Тест здібностей відрізняється від тесту досягнень тим, що спрямований на виявлення потенційного, а не наявного на даний момент знання тестованого.
Основна мета контролю знань і умінь полягає у виявленні досягнень, успіхів учнів; у вказівці шляхів вдосконалення, поглиблення знань, умінь, з тим, щоб створювалися умови для подальшого включення школярів в активну творчу діяльність.

Ця мета, в першу чергу, пов'язана з визначенням якості засвоєння навчального матеріалу учнями – рівня оволодіння знаннями, уміннями і навичками, передбаченими програмою – з математики, зокрема.

Навчальна функція контролю полягає у вдосконаленні знань і умінь, їх систематизації. В процесі перевірки учні повторюють і закріплюють вивчений матеріал. Вони не лише відтворюють раніше вивчене, але і застосовують знання і уміння в новій ситуації.

Перевірка допомагає школярам виділити головне в матеріалі, що вивчається, зробити знання, що перевіряються, і уміння яснішими і точнішими. Контроль сприяє також узагальненню і систематизації знань.
Суть діагностичної функції контролю в отриманні інформації про помилки, недоліки і пропуски в знаннях і уміннях учнів і причинах ускладнень учнів у оволодінні навчальним матеріалом, про кількість і характер помилок.

Прогностична функція перевірки служить отриманню випереджаючої інформації про навчально-виховний процес. У результаті перевірки отримують підстави для прогнозу про хід певного відрізку навчального процесу: чи досить сформовані конкретні знання, уміння і навички для засвоєння подальшої порції навчального матеріалу (розділу, теми).

Розвиваюча функція контролю полягає в стимулюванні пізнавальної активності учнів, в розвитку їх творчих здібностей. [4]

 

1.2 Конструювання тестів по формуванню функціональної математичної грамотності учнів

 

Для конструювання тестових завдань з математики потрібна теоретична база, що включає наступні основні питання: тестові технології в навчанні; понятійний апарат педагогічної системи "Міжнародна програма оцінки навчальних досягнень 15-річних учнів (Program for International Student Assessment – PISA) ".

Основою високого рівня математичної освіти на різних етапах  навчання є математична грамотність підростаючого покоління в більш широкому сенсі. Тому забезпечення математичною грамотністю школярів є першочерговим завданням у справі забезпечення якості шкільної математичної освіти.

У дослідженнях PISA поняття математична грамотність уточнюється таким чином.

Математична грамотність – це здатність учнів:

• розпізнавати проблеми, що виникають в навколишній дійсності і які можна вирішити засобами математики;
• формулювати ці проблеми на мові математики;
• розв’язувати ці проблеми, використовуючи математичні факти і методи;
• аналізувати використані методи розв’язання;
• інтерпретувати отримані результати з урахуванням поставленої проблеми;
• формулювати і записувати результати розв’язку.

Іншими словами, можна сказати, що під математичною грамотністю розуміється здатність людини розуміти і займатися математикою, висловлювати добре обгрунтовані судження відносно ролі математики. Ця здатність потрібна для поточного і майбутнього особистого, професійного і громадського життя індивіда в сім'ї і суспільстві, а також для життя творчого, зацікавленого і мислячого громадянина.

Сам термін "грамотність" має специфічний зміст в цьому дослідженні. Тут під грамотністю розуміється швидше здатність функціонально використати математичні знання і уміння, ніж майстерне володіння цими знаннями у рамках вимог шкільної програми. І цю здатність можна називати функціональною математичною грамотністю.

Отже, функціональна математична грамотність – це здатність людини визначати і розуміти роль математики у світі, в якому вона живе, висловлювати добре обгрунтовані математичні судження і використати математику так, щоб задовольняти в сьогоденні і в майбутньому потреби, властиві творчому, зацікавленому і мислячому громадянину. [4]

 

1.3 Міжнародна програма оцінки навчальних досягнень учнів PISA 

 

PISA – це дослідження, яке проводиться Організацією економічного співробітництва і розвитку (ОЕСР) та визначає, як учні загальноосвітніх шкіл навчилися використовувати здобуті знання на практиці.

PISA проводиться трьохрічними циклами з 2000 р.

 Основною метою дослідження PISA є отримання надійних відомостей про результати навчання у різних країнах світу, які можна порівняти на міжнародному рівні. Передбачається, що отримані відомості нададуть можливість країнам­учасницям приймати обґрунтовані рішення для визначення перспектив розвитку галузі освіти.

 Вимірювання знань проводиться серед учнів 15­річного віку. Такий вибір визначено тим, що в багатьох країнах до цього віку закінчується обов’язкове навчання в школах і навчальні програми мають багато спільного. Особливим інтересом дослідження є визначення стану знань та вмінь, які можуть бути корисними для учнів у майбутньому, а також уміння самостійно здобувати знання, потрібні для успішної адаптації в сучасному світі. Оцінка підготовки 15­річних підлітків стандартизована. Матеріали розробляються країнами-учасницями міжнародної програми спільно.

 Щодо змісту дослідження, то воно проводиться за трьома напрямками: «грамотність читання», «математична грамотність» та «природничо-наукова грамотність». Особлива увага приділяється виявленню рівня розуміння учнями основних понять, опанування основними методами в рамках вищезазначених напрямів та вміння використовувати свої знання в різних ситуаціях. Тобто вимірюється не рівень опанування конкретним змістом навчальних дисциплін, а рівень більш широких знань та умінь, які накопичені під час вивчення шкільних предметів і потрібні для дорослого життя. Велика увага також приділяється оцінці міжпредметних компетентностей учнів.

 У дослідженні PISA оцінюються такі вміння учнів, як мислення, аргументація, постановка і вирішення проблем, моделювання, використання різних методів представлення результатів. Таким чином навчальна компетентність учасників міжнародного іспиту визначалася за трьома навчально­пізнавальними видами діяльності — відтворення, застосування й міркування.

 Основним методом є письмова форма контролю – тести. Для їх виконання учням дається 120 хв. Тести складаються із завдань двох типів: із готовими відповідями, серед яких треба вибрати правильну, та завдань, на які учень має дати власну стислу або повну відповідь. Деякі завдання складаються з низки питань різної складності стосовно окремої життєвої ситуації.

 Технологія оцінювання грамотності школярів за трьома напрямками дослідження дає змогу визначити, наскільки добре учасники проекту PISA можуть екстраполювати отримані знання і застосовувати їх поза школою. Цей підхід відображає той факт, що сучасна економіка заохочує суспільство, де на високому професійному рівні застосовуються академічні знання. У цьому зв’язку технологія оцінювання дослідження функціональної грамотності включає шість рівнів освітніх досягнень 15­річних учнів понад 60 країн світу. Найвища планка – 5 і 6 рівень – уміння самостійно мислити, аналізувати і висувати власні гіпотези, 4-3 – здатність використовувати наявні знання та вміння для отримання нової інформації, 2 – вміння застосувати наявні знання та навички в простих не навчальних ситуаціях, 1 рівень – низький рівень елементарних знань і невелика ймовірність успішного виконання завдань.

 У 2012 р. учасникам Міжнародної програми з оцінки освітніх досягнень учнів PISA вперше в історії масового тестування та оцінки був запропонований новий тип завдань – інтерактивні задачі з багатофакторними об’єктами.

 У 2015 р. пропоновані школярам завдання стали вже кооперативно­ інтерактивними: учасник повинен буде досліджувати запропоновану йому нову систему спільно з іншим учасником. [1]

 Дослідження PISA складається з двох блоків: опитування і тестування. 

 Опитування потрібне для того, щоб з'ясувати, які саме фактори впливають на успішність учнів у виконанні завдань тестування. Наприклад, є дуже великий блок запитань про background дитини: де вона народилася, хто її батьки і яка в них професія, які шкільні предмети вона вивчала, чи комфортно почувається в середовищі однолітків у школі, чи подобається їй навчатися, чи любить вона ті або інші уроки? 

 Для чого потрібне тестування, зрозуміло – щоб дитина показала, що вона вміє робити зі своїми знаннями в різноманітних життєвих ситуаціях. [2]

 

Розділ 2. Особливості тестових завдань по програмі PISA

 

2.1 Методика конструювання тестових завдань по математиці в контексті міжнародної програми PISA

Завдання для тестів PISA готує Міжнародний консорціум фахівців з більш як 40 країн світу. Усі завдання проходять серйозні етапи підготовки. Спочатку дослідники пропонують певні ситуації для розгляду, потім збираються для того, щоб обговорити ті ситуації, розробляють для них завдання. Кожна країна отримує ці завдання і надає коментарі щодо того, чи відповідають вони освітньому контенту цієї країни.

Завдання для школярів з різних країн при цьому абсолютно однакові. Це дозволяє порівнювати результати і робити якісь висновки. 

Тести PISA вимірюють, зокрема, математичну грамотність. Завдання тестів PISA вимірюють досягнення у математиці на потреби дня і включають в себе задачі, що не стосуються вивчення математики як системи знань.

Цілі і завдання міжнародного дослідження PISA в області "Функціональної математичної грамотності" такі:

Мета – оцінити функціональну математичну грамотність 15-16-річних учнів загальної середньої, технічної і професійної освіти.

Завдання:

• виявлення математичної здібності 15-річних учнів використати отримані знання і уміння для вирішення широкого кола проблем, що виникають в повсякденному житті і виявити тенденції розвитку цих здібностей;
• визначення стратегій розвитку системи освіти як з точки зору змісту і методів навчання в цілому, так і з точки зору дії контекстних чинників (модель управління, мова навчання, соціальний статус сім'ї та ін.) на рівень розвитку функціональної математичної грамотності школярів;
• аналіз реальних результатів, отриманих у рамках об'єктивних вимірів на основі інструментарію, що відбиває світові пріоритети в області освіти і отримання з них науково обґрунтованих і творчих для освітньої політики висновків.

Ключове питання дослідження: «Чи володіють учні 15-річного віку, які отримали основну загальну освіту, знаннями і уміннями, необхідними їм для повноцінного функціонування в суспільстві»? Вибір цих учнів пояснюється тим, що у багатьох країнах до цього віку завершується обов'язкове навчання в школі, тому програми навчання в різних країнах мають багато спільного. Саме на цьому етапі освіти важливо визначити стан тих математичних знань і умінь, які можуть бути корисні учням в майбутньому, а також оцінити математичні здібності учнів самостійно здобувати знання, необхідні для успішної адаптації в сучасному світі.

За задумом ідеологів дослідження, тест PISA – це тест, що виявляє життєвість освітніх результатів по відношенню до запитів часу і очікувань замовників.

Особливий інтерес на етапі закінчення обов'язкової освіти представляють вже не отримані знання і уміння предметного характеру, а те, наскільки вони можуть бути застосовані і корисні учням в майбутньому, наскільки навчання в школі підготувало їх до самостійного навчання, до самостійного добування необхідної інформації і ширше – до успішної адаптації в сучасному суспільстві. [1]

 

 

2.2 Класифікація завдань

 

Тестові завдання з математики в тестах PISA класифікуються за компетентністю, за типами, за оцінюванням знань, за рівнями складності:

• за компетентністю (рівні компетентності);
• за оцінюванням знань (математична область, фундаментальні математичні ідеї);
• за типами (з вибором відповіді, з короткою відповіддю, із структурованими питаннями);
• за рівнями складності (від найнижчого – рівень 1, до найвищого – рівень 6).

В якості фундаментальних математичних ідей пропонуються наступні області: кількість, простір і форма, змінні й залежності, невизначеність.

При оцінюванні виконання учнями завдань PISA застосовуються три види оцінок: "правильно", "частково правильно" і "неправильно". Це дуже принципово, що є частково правильна відповідь, коли учень в чомусь має рацію, а щось упустив.

 

2.3 Компетентнісний підхід в освіті

 За результатами першого дослідження PISA (1999 р.) велике число країн показало невисокі результати рівня функціональної математичної грамотності учнів 15-річного віку, що притягнуло підвищену увагу у світі до перевірки компетентності випускників школи в області математики.

 Якщо ми говоримо про дослідження PISA, то це передусім компетентнісний підхід, компетентнісне оцінювання і звернення до компетентнісної парадигми освіти, яка в світі вже давно є передовою. 

 Компетентнісний підхід в освіті в протилежність концепції "засвоєння знань" (суми інформації (відомостей)), припускає освоєння учнями різного роду умінь, що дозволяють їм в майбутньому діяти ефективно в ситуаціях професійного, особистого і громадського життя. У компетентнісному підході особливе значення надається умінням, що дозволяють діяти в нових, невизначених, проблемних ситуаціях, для яких заздалегідь не можна напрацювати відповідних засобів. Їх треба знаходити в процесі розв’язання подібних ситуацій і досягати необхідних результатів.

 Математична компетентність – це здатність структурувати дані (ситуацію), виділяти математичні відношення, створювати математичну модель ситуації, аналізувати і перетворювати її, інтерпретувати отримані результати. Іншими словами, математична компетентність учня сприяє адекватному застосуванню математики для вирішення проблем, що виникають в повсякденному житті.

 Це поєднання математичних знань, умінь, досвіду і здібностей людини, що забезпечують успішне розв’язання різних проблем і завдань, що вимагають використання математики.

 Наприклад, якщо ми говоримо про математичні задачі. Усі в школі вчили формулу площі квадрата чи прямокутника. Але людина, яка робить ремонт у своїй ванній кімнаті, має порахувати цю площу для того, щоб визначити кількість кахлів, які треба покласти на підлогу в ній. Це і є компетентнісний підхід. [5]

 Таким чином, компетентнісний підхід є посиленням прикладного, практичного характеру усієї шкільної освіти (у тому числі і предметного навчання).

 

Розділ 3. Приклади практико-орієнтованих завдань у форматі тестових завдань PISA

 

3.1 Приклади тестових завдань з програми PISA за рівнем компетентності та їх комплексний аналіз

Для опису рівнів математичної компетентності в дослідженні PISA виділені види діяльності, що їм відповідають:

а) відтворення, визначення і обчислення;

б) зв'язки і інтеграція, необхідні для вирішення проблеми;

в) математизація, математичне мислення, узагальнення і інтуїція.

 В цілому ці види діяльності перераховані за збільшенням складності.

а) Перший рівень компетентності включає види діяльності, які перевіряються у багатьох стандартизованих тестах, а також в порівняльних міжнародних дослідженнях в основному за допомогою такої форми завдань, як завдання з вибором відповіді.

Цей рівень компетентності пов'язаний зі знанням фактів, відтворенням властивостей, пізнаванням еквівалентних математичних об'єктів, виконанням стандартних процедур, використанням стандартних алгоритмів і розвитком технічної сторони алгоритмічних умінь.

Приклади  першого рівня компетентності :
1. Розв’яжіть рівняння: 7х - 3 = 13х +15.
2. Яке число є середнім арифметичним чисел 7, 8, 14, 15, 9?
3. Запишіть 69% у вигляді звичайного дробу.
4. Відрізок m
називається___________ круга

 

 

б) Другий рівень компетентності включає встановлення зв'язків між різними областями, розділами і темами математики і інтеграцію їх матеріалу з метою розв’язування нескладних завдань. Ці завдання не можна віднести до стандартних, проте вони не вимагають значної математизації, представленої в них ситуації.

У рамках цього рівня компетентності учні повинні проявити уміння представити присутню в умові завдання інформацію відповідно до цієї ситуації і згідно з питанням, поставленим в завданні. При встановленні зв'язків між матеріалом з різних розділів математики від учнів потрібні уміння розрізняти і співвідносити визначення, умови, доведення, твердження, приклади. У цей рівень компетентності включається також уміння розкривати і інтерпретувати сенс записів, зроблених на формальній мові з використанням різних символів, перекласти їх на звичайну мову. В умовах завдань, які віднесені до цього рівня компетентності, часто пропонується деяка ситуація, що вимагає від учнів ухвалення рішення, пов'язаного з особливостями цієї ситуації.

Приклади другого рівня компетентності:

1. Ви проїхали на машині дві третини шляху. На початку шляху бензобак машини був повний, а зараз він заповнений на одну чверть. Чи вважаєте ви, що у вас є проблема?

2. Мері живе за кілометр від школи, Мартин – за п'ять. Яка відстань між будинками Мері і Мартіна?

3. У класі 28 учнів. Відношення числа дівчаток до числа хлопчиків дорівнює 4:3. Скільки дівчаток в класі?

в) Третій рівень компетентності вимагає від учнів скласти математичну модель запропонованої ситуації: дізнатися і витягнути з умови математичну частину, поміщену в запропоновану інформацію, і використати математику для розв’язання проблеми, самостійно розробити, проаналізувати й інтерпретувати створену математичну модель ситуації, розробити свій спосіб розв’язання і його математичну аргументацію, включаючи необхідні доведення і узагальнення. [4]

Ця діяльність включає критичне мислення, аналіз і роздуми. Учні не лише мають бути здатні розв'язати запропоновану проблему, але також і сформулювати її відповідно до ситуації, що розглядається в завданні, а також мати глибоке розуміння суті і можливостей математики як науки.

Цей рівень компетентності є серцевиною функціональної математичної грамотності і представляє значні труднощі для тестування. Для оцінки його досягнення не підходять завдання з вибором відповіді. Найбільше підходять для цього завдання з вільною відповіддю, розробка і оцінка виконання яких дуже обмежена.

Приклади третього рівня компетентності:

1. У одній з країн в 1980 р. з національного бюджету на оборону виділялося 30 мільйонів доларів. Загальний бюджет на цей рік склав 500 мільйонів доларів. Наступного року, на оборону було виділено 35 мільйонів при загальному бюджеті в 605 мільйонів доларів. Інфляція за ці два роки склала 10 відсотків.

а) Ви запрошені прочитати лекцію в товаристві пацифістів. Ви маєте намір показати, що бюджет на оборону за цей час скоротився. Поясніть, як ви це зробите.
б) Ви запрошені прочитати лекцію у військовій академії. Ви маєте намір показати, що бюджет на оборону збільшився за цей період. Поясніть, як ви це зробите.

Характеристика цих рівнів дає можливість дійти наступних висновків:
- компетентність проявляється в розв’язанні завдань, що потребують застосування набутих умінь в умовах, що дещо відрізняються від знайомих учням. При цьому не передбачається значний об'єм математичних умінь, нестандартність завдань забезпечується, передусім, їх прикладною спрямованістю;
- рівні компетентності відрізняються складом когнітивних прийомів діяльності (розпізнавання, відтворення, встановлення зв'язків між даними в умові завдання, інтерпретація розв’язання, встановлення закономірностей, проведення узагальнення і т. п.).

Матеріали дослідження показують ієрархічність рівнів компетентностей, тобто завдання другого рівня компетентності складніші за перший рівень, а третій рівень – складніший від двох попередніх. Завдання третього рівня відрізняються від знайомих математичних завдань, характерних для завдань першого і в деяких випадках другого рівня компетентності, і вимагає для свого розв’язання не лише міцних технічних навичок, але і високого математичного розвитку, інтуїції, логічного мислення і тому подібне.

 

3.2 Приклади практико-орієнтовних завдань в форматі PISA та їх аналіз

У цьому розділі наведені приклади практико-орієнтовних завдань у форматі PISA, а також даний їх аналіз з точки зору формату завдань і рівнів компетентностей.

Задача 1. «Звіт»

Джерелом інформації для складання річного звіту є наступна таблиця:

Кількість учнів в школі (чол.)	«5» (чол.)	«4» і «5» (чол.)	«3» (чол.)
720	36	288	360

 

Питання 1: Необхідно підготувати звіт підсумків навчального року:

1. % учнів, які мають оцінку "5" _____________ %

2. % учнів, що мають оцінки "4" і "5" __________%

3. % учнів, що мають оцінку "3" ______________ %

4. % учнів, що мають оцінку "2", ______________%

Формат питання: конструйований.
Компетентність: 1-рівень.
Для розв’язання цього завдання учень повинен мати наступні компетенції:
- знаходити відсоток від числа;
- уміти обчислювати.

 

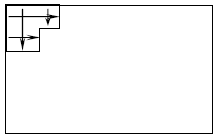
Задача 2. «Диспетчер»

Ви працюєте диспетчером на станції "Швидка допомога". За викликом Вам необхідно відправити машину від пункту А (станція "Швидка допомога") в пункт Д за нижче наведеною схемою.

 

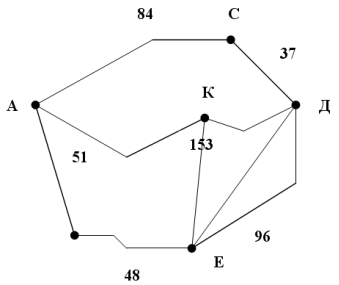
Питання 1:

За цією схемою виберіть найбільш короткий маршрут руху машини швидкої допомоги від станції "Швидка допомога" (А) до пункту Д.
Підкресліть правильну відповідь:

А)   АКД            В)   АСД         С)   АЕД            D)  АКЕД

Формат питання:  простий – з вибором відповіді.

Компетентність:  1-й рівень.

Питання 2:

Ви складаєте іспит на профпридатність. Нашвидку прочитайте текст завдання: "З двох пунктів А і В один назустріч одному виїхали вантажна і легкова машини. У пункті С вони зустрілися. Швидкість легкової машини на 20 км/год більше швидкості вантажної. Необхідно знайти швидкості обох машин, якщо відстань між пунктами 200 км".

Якої інформації бракує для його розв’язання? Обведіть правильну відповідь:
А) Швидкість вантажної автомашини.
В) Швидкість легкової автомашини.
С) Час, який була в дорозі кожна машина.
D) Місце зустрічі вантажної і легкової машин.

Формат питання: простий – з вибором відповіді.

Компетентність: 2-й рівень.

Питання 3:

Задайте необхідну інформацію і знайдіть швидкості обох машин.
Наведіть розв’язання __________________________________________________
Швидкість вантажної автомашини _____________ км/год.
Швидкість легкової автомашини _____________ км/год.

Формат питання: конструйований.

Компетентність: 3-й рівень.

Для розв’язання цього завдання учень повинен мати наступні компетенції:

1.               уміти аналізувати умову завдання;
2.              знати формулу обчислення швидкості;
3.               знати алгоритм розв’язування завдань на спільний рух;
4.              уміти перекладати умову завдання математичною мовою (моделювати ситуації завдання) і оцінювати дані за умовою;
5.               творчо підходити до вибору математичного інструментарію;
6.                самостійно розробити алгоритм дій;
7.              узагальнити і обґрунтувати отримані результати. [4]

 

 

3.3 Завдання, що відповідають шкільній програмі 5-9 класів та їх розв’язання

Наиведемо декілька відредагованих текстових завдань з різних джерел (шкільних підручників, інтернет-ресурсів), їх інтерпретації в практико-орієнтовані завдання у форматі PISA, а також розв’яжемо ці завдання.

Задача 1. «Кроки» [8]

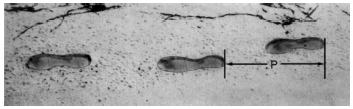
На знімку зображено сліди людини, які вона залишила на піску. Довжина кроку – відстань між двома сусідніми слідами. P

Залежність між числом кроків дорослого чоловіка й довжиною його кроку наближено виражається формулою n/P=140, де n – кількість кроків за одну хвилину, P – довжина кроку в метрах.

Завдання 1. Використовуючи наведену формулу, обчисліть довжину кроку Андрія, якщо він робить 70 кроків за хвилину.

 Розв’язання:

 За даною формулою отримуємо:

За умовою Андрій робить 70 кроків за хвилину, значить, n = 70. Довжина його кроку (в метрах) дорівнює .

Відповідь: 0,5 м.

Завдання 2. Богдан знає, що довжина його кроку дорівнює 0,80 м. Застосовуючи наведену вище формулу, обчисліть швидкість пересування Богдана в метрах за секунду та в кілометрах за годину.

Розв’язання

За даною формулою отримуємо:

За умовою довжина кроку Богдана дорівнює Р=0,80 м. За хвилину він робить кроків.

Тобто, за хвилину Богдан проходить

Швидкість Богдана дорівнює

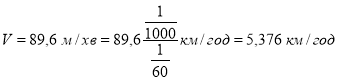
Відповідь:

 

Задача 2. «Клумби» [8]

Садівник має 32 метри дерев’яної огорожі й хоче обнести нею клумбу. Він обирає форму клумби із таких варіантів:

Обведіть «Так» або «Ні» для кожної форми клумби залежно від того, чи вистачить 32 м огорожі, щоб обнести нею клумбу.

Розв’язання

Можна помітити, що периметри фігур A, C і D дорівнюють 32 м. Дійсно, перенесенням частин без зміни їх довжини з фігури D можна отримати фігури A і C (див. мал.).

Сума довжин маленьких вертикальних ділянок дає велику вертикаль. Аналогічно з горизонтальними ділянками.

 

Оскільки висота паралелограма (фігура B) дорівнює 6 м, то довжина його бічної сторони більше 6 м. Значить, сума довжин двох його бічних сторін більше 12 м. І разом з довжинами двох основ по 10 м вийде більше

32 м периметра. Для фігур A, C і D огорожі вистачить, а для фігури B – ні.

Відповідь: так, ні, так, так.

 

Задача 3. «Приватний будинок» [10]

 

На світлині зображено приватний будинок, дах якого має форму піраміди.

Нижче наведено рисунок побудованої учнями математичної моделі даху цього будинку із зазначенням довжини деяких відрізків.

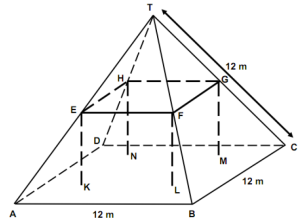
Нижня частина даху будинку в моделі є квадратом ABCD. Стійки, на які спирається дах, є ребрами бетонного блоку, що має форму прямокутного паралелепіпеда EFGHKLMN. Точка E – середина ребра AT, F – середина BT, G – середина CT, H – середина DT. Усі ребра піраміди дорівнюють 12 м.

Завдання 1. Обчисліть площу підлоги горища – квадрата ABCD.

Розв’язання

Довжина сторони квадрата ABCD дорівнює 12 м.

Тоді його площа: S = 12² = 144 кв. м.

Відповідь: 144 м².

Завдання 2. Знайдіть довжину відрізка EF – горизонтального ребра бетонного блока.

Розв’язання

Оскільки E – середина ребра AT, а F – середина BT, значить, EF – середня лінія трикутника ABT. Тому EF в 2 рази менше довжини відрізка AB: 12 : 2 = 6 м.

Відповідь: EF =  6  м.

 

Задача 4. «Будматеріали» [4]

Будівельній фірмі потрібно придбати 75 кубометрів пінобетону у одного з трьох постачальників.  Ціни і умови доставки наведені в таблиці. 

Постачальник	Вартість пінобетону (тг. за  м³)	Вартість доставки (тг.)	Додаткові умови
А	2650	4500
Б	2700	5500	При замовленні на суму більше 150000 тг.  доставка безкоштовно
В	2680	3500	При замовленні понад 80 м³  доставка безкоштовно

 

Питання 1. Якого постачальника вибирає будівельна фірма?  Запишіть пояснення своєї відповіді

Для вирішення даного завдання учень здатний встановлювати відмінності між різними формами подання інформації в ситуації, описаної в задачі;  знаходити раціональний вибір в контексті ситуації, описаної в задачі;  грамотно зробити обчислення.

Розв’язання

 А) 75 • 2650 + 4500 = 203250 (тенге);

 Б) 75 • 2700 + 0 = 202500 (тенге); В) 75 • 2680 + 3500 = 204500 (тенге).

Постачальник Б, так як, при виборі цього постачальника ціна за товар і доставки буде найдешевша, ніж при виборі інших постачальників. 

Відповідь: Б.

Характерною особливістю наведених завдань є їх розв’язуваність  математичними методами і виражена практична спрямованість.

 

3.4. Порівняльний аналіз тестування ЗНО і PISA

Якщо провести порівняння між структурою завдань тестів ЗНО та PISA, то можна стверджувати, що у Міжнародному тестуванні PISA і окремими практико-орієнтованими завданнями ЗНО є багато спільного: типологія завдань дуже схожа і перевіряє уміння учнів використовувати математичну грамотність у реальних життєвих ситуаціях. Суттєвим недоліком ЗНО у порівнянні з тестуванням PISA є те, що кількість таких завдань у першому становить лише 3-6%, тоді коли другий на всі 100% складається із завдань, у яких вирішуються реальні життєві питання за допомогою математичних компетентностей.

Нижче наведено дві аналогічні за змістом задачі з тестування PISA та ЗНО.

Задача 1. «Тарифний план» (PISA) [4]

 

 

 

 

 

Мережа мобільного зв’язку пропонує на вибір три тарифних плани:

Тарифний план	Абонентська плата	Плата за 1 хвилину розмов
1. Погодинний	980 тг. в місяць	7 тг.
2. Комбінований	1000 тг. за 500 хв. в місяць	3 тг. за 1 хвилину, понад 500 хв. в місяць.
3. Безлімітний	1500 тг.	0 тг.

 

Абонент вибрав найдешевший тарифний план, вважаючи, що тривалість розмов становить 650 хвилин в місяць.

Питання 1. Який тарифний план обрав користувач?

Питання 2. Яку суму заплатить користувач за місяць, якщо загальна тривалість розмов дійсно буде 650 хвилин?

Відповідь: 1) «Безлімітний»; 2) 1500 тенге.

 

Задача 2. ( ЗНО 2017) [9]

Для поповнення рахунку телефону Андрій уніс певну суму грошей до платіжного термінала. З цієї суми утримано комісійний платіж у розмірі 2 грн. 40 коп., що становить 3% від суми, унесеної до терміналу. У результаті рахунок телефону поповнено на решту внесеної суми.

Питання 1. Яку суму грошей уніс Андрій до платіжного терміналу?

Питання 2. Мобільний оператор, послугами якого користується Андрій,нараховує 8 бонусів за кожні 5 грн., на які поповнено рахунок телефону. На залишок грошей, менший за 5 грн., бонуси не нараховуються. Скільки бонусів нараховано Андрію за здійснене ним поповнення телефону?

Відповідь: 1) 80 грн. ; 2) 120.

Для розв’язування таких задач потрібні вміння встановлювати відмінності між різними формами подання інформації в ситуації, описаній у задачі; знаходить раціональний вибір у контексті ситуації, описаній у задачі; грамотно виконати обчислення.

Розділ 4. Банк математичних завдань та їх класифікація

 

 У даному розділі буде розібрано завдання, що відповідають шкільній програмі 5-9 класів, представлені в форматі тестових завдань програми PISA.

 Компетентнісно-орієнтовані завдання повинні бути включені в навчання не тільки на етапі моніторингу набутих компетентностей, а й на етапі їх формування. 

 

Задача 1. «Обсяг і маса» [4]

 

       

Виміри прямокутного паралелепіпеда, виготовленого з ясена, 8 см, 6 см і 4 см. Ребро куба, виготовленого з бальзового дерева, 12 см.

Питання 1. Чому дорівнюють об’єм паралелепіпеда і куба?

А) 192 , 1728; B) 192, 1738;

C) 212 , 1738 D) 200, 1828.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 1-й рівень.

Область змісту: кількість.

Ситуація: наукова.

Для вирішення даного завдання необхідно знати формули об’єму паралелепіпеда і куба, вміти їх обчислювати.

Питання 2. Маса 1 ясена – 0,75 г, а 1 бальзового дерева – 0,25 г. Знайти маси прямокутного паралелепіпеда і куба в кг.

Компетентність: 1 рівень - відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-рівень.

Область змісту: кількість.

Ситуація: наукова.

Для вирішення даного завдання потрібно вміти використовувати дані першого завдання і обчислювати маси паралелепіпеда і куба, використовуючи відповідну інформацію з даних завдань, перетворювати одиниці вимірювання.

Відповідь: 1) А; 2) 144; 432. 

 

Задача 2. «Дачний будиночок» [8]

Борис вирішив побудувати будиночок на садовій ділянці. Для укладання фундаменту він купив 264 цеглин по 200 тг. за штуку, 5 мішків цементу по 3000 тг. за мішок і 24 шматка арматури (товстого дроту) по 100 тг. за шматок.

Питання 1.У скільки обійшовся Борису фундамент садового будиночка?

Питання 2. Щоб визначити число рядів цегли в стіні будинку висотою 3 метри, він виміряв висоту 20 рядів цегли, яка виявилася 1,5 м. Як знайти висоту цегли?

Питання 3. Чому дорівнює число рядів цегли?

Компетентність: 1-й рівень відтворення.

Рівень досягнень: 1-й рівень.

Область змісту: кількість.

Ситуація: у питанні 1 – життєва, у 2 і 3 – наукова.

Відповідь: 1) 70200 тг. ; 2) 7,5 см; 3) 40 рядів.

 

 

Задача 3. «Пальто» [4]

У березні місяці в магазині була оголошена знижка на зимове пальто. Ніна купила пальто, що коштувало

 25 000 грн. за 18 750 грн.

Питання : Скільки відсотків склала знижка?

Компетентність: 2-й рівень – встановлення зв'язків.

Рівень досягнень: 3 рівень.

Область змісту: кількість.

Ситуація: соціальна.

Відповідь: 25%.

 

Задача 4. «Квіткові ящики» [5]

Із листа фанери розміром 22080 см для квіткових ящиків потрібно вирізати рівнобічні трапеції з основами 30 см і 10 см та гострим кутом 45°, зробивши розмітки найбільш раціональним способом.

Питання. Уточнити масштаб і знайти розмітку, зроблену найбільш раціональним способом.

А

 

 

B

 

 

C

1

D

 

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умови завдання, при вирішенні стандартних завдань).

Рівень досягнення: 4-рівень.

Ситуація: наукова.

Відповідь:

Масштаб: сторони квадратної клітини – 1 см; раціональний спосіб – В.

 

Задача 5. «Квадрат» [8]

Є 9 паличок різної довжини від 1 до 9 см. Скількома способами можна скласти з цих паличок квадрати, і які їхні сторони?

Примітка. Необов'язково використовувати всі палички, способи виготовлення одного квадрата вважаються різними, якщо використані різні палички.

Компетентність: 2-й рівень встановлення зв'язків.

Рівень досягнення: 3-й.

Ситуація: навчання.

Розв’язання:

Легко бачити, що для складання квадрата буде потрібно не менше 7 паличок. Тому не можна скласти квадрат із стороною менш як 7 см. З іншого боку, сума довжин всіх паличок дорівнює 45см, і тому з них не можна скласти квадрат зі стороною понад 11см. З паличок даного набору можна скласти відрізки довжиною 7, 8, 9, 10 і 11см такими способами:

7 = 6 + 1 = 5 + 2 = 4 + 3;

8 = 7 + 1 = 6 + 2 = 5 + 3;

9 = 8 + 1 = 7 + 2 = 6 + 3 = 5 + 4;

9 + 1 = 8 + 2 = 7 + 3 = 6 + 4;

9 + 2 = 8 + 3 = 7 + 4 = 6 + 5.

Отже, з даного набору можна скласти квадрат зі стороною 7 рівно одним способом (його боки складаються з паличок довжиною 7 см, тобто

6 + 1, 5 + 2 і 4 + 3), зі стороною 8, 10 і 11 також одним способом , а квадрат зі стороною 9 см – п'ятьма способами.

Відповідь: квадрати зі стороною 7, 8, 10, 11 см – одним способом, зі стороною 9 см - п'ятьма способами. Всього 9 способів.

 

Задача 6. «Колона машин» [3, c. 87]

 

                  

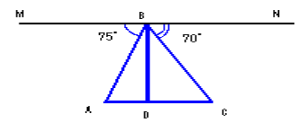
З вертольота , що знаходиться над дорогою, видно колону машин, що рухається. Початок колони видно під кутом , а її кінець – під кутом . Вертоліт знаходиться на висоті 1650 м.

Питання 1. Яка довжина колони? Відповідь округліть до цілих.

Примітка: = 0,2679; = 0,3640.

Компетентність: 2-й рівень – встановлення зв'язків.

Рівень досягнення: 3-й рівень.

Ситуація: наукова.

Розв’язання. Нехай А – початок колони, С – її кінець;

 тоді АС = АD + DC. За умовою МВА = 75°, NBC = 70° , тому

 АВD = 15°, СВD = 20°;

 АС = ВD·+BD·  442+800 = 1042 м.

Відповідь: довжина колони 1042м.

 

Задача 7. «Палітурна майстерня» 

                

Одна з палітурних майстерень бере по 240 тг. за книгу і ще 700 тг. за оформлення замовлення, а інша – по 280 тг. за книгу і 450 тг. за оформлення замовлення.

Питання 1. Заповніть таблицю:

Кількість замовлених книг (п)	Ціна замовлення в першій майстерні	Ціна замовлення в другій майстерні
1	940	730
2
3
4
5

 

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й рівень.

Ситуація: наукова.

Для вирішення даного завдання необхідно вміти направляти мислення і складати точне тлумачення даних.

Кількість замовлених книг (п)	Ціна замовлення в першій майстерні	Ціна замовлення в другій майстерні
1	940	730
2	1180	1010
3	1420	1290
4	1660	1570
5	1900	1850

 

 

 

 

Задача 8. «Подача води» [4]

Вода тече по двох трубах з однаковою швидкістю. Перша труба має діаметр = 20см, а друга – = 15см.

Питання. У скільки разів подача води в першій трубі більше, ніж у другій?

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й рівень.

Ситуація: наукова.

Розв’язання:

Відповідь: 1,8 раз.

 

Задача 9. «Газон» [4]

    

 

На прямокутному заводському подвір'ї розміром 150110 м, завантаженому будівлями, хочуть розбити круглий газон радіусом 5м. Там стоїть 10 складів, розміри яких 2020 м, 4 цехи розміром 4010м і кругле бензосховище радіусом 10м.

Питання 1.Чи можна розбити газон даного розміру на території заводу: «Так» або «Ні».

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й рівень.

Ситуація: наукова.

Питання 2. Чи можна розбити газон даного розміру на території заводу незалежно від розташування будівель?

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при вирішенні стандартних завдань).

Рівень досягнення: 3-й рівень.

Ситуація: наукова.

Відповідь: 1) «Так»;

2) Вказівка: знайти відношення і зробити відповідні висновки.

 

Задача 10. «Учні Піфагора» [5]

Скажи мені, знаменитий Піфагор, скільки учнів відвідують твою школу, слухають твої бесіди?

• Ось скільки, – відповів Піфагор, 50% вивчає математику, 25% –природу, сьома частина проводить час в міркуванні, і, крім того, є ще 3 жінки.

Питання. Скільки учнів у Піфагора?

Компетентність: 2-й рівень – встановлення зв'язків.

Рівень досягнення: 3-й.

Ситуація: навчання.

Розв’язання: нехай х чол. відвідують лекції, 50% від х чол. () вивчають математику, 25% від х чол. () вивчають природу, чол. розмірковують.

Маємо:

.

Відповідь: 28 чоловік.

 

Задача 11. «Забіг» [4]

 У таблиці наведено результати забігу шести восьмикласників на 200м.

Номер доріжки	I	II	III	IV	V	VI
Результат  (в с)	30,1	27,3	28,9	28,5	27,8	24,3

Залік ставиться за результат не більше 28,3с.

Питання 1: З яких доріжок бігли учні, які отримали залік?

А) I, II, III;

В) II, III, V;

С) II, V, VI;

D) I, V, VI.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 1-й рівень.

Область змісту: кількість. 

Ситуація: шкільне життя.

Для розв’язання даного завдання учень вміє: виключати зайві дані (забіг на 200 м), порівнювати десяткові дроби, витягувати інформацію з таблиці; володіє поняттям «не більше». При цьому тільки два вміння є чисто предметними, інші – загальноосвітніми. 

Відповідь: 1) С.

 

Задача 12. «Пароплав» [4]

Швидкість пароплава у стоячій воді 23,7 км /год, а швидкість течії річки 2,8 км/год.

Питання 1. Скільки кілометрів пройшов пароплав за течією річки за 2,4 години?

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: змінні й залежності.

Ситуація: наукова.

Для розв’язання даного завдання учень повинен знати залежності між швидкістю, шляхом  і часом, вміти використовувати формулу цієї залежності з урахуванням ситуації, розглянутої в задачі (проти течії).

Питання 2. Скільки км може проїхати пароплав за цей же час проти течії річки?  Відповідь обґрунтувати.

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при вирішенні стандартних завдань і пояснення процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: змінні й залежності.

Ситуація: наукова.

Для розв’язання  даного завдання учень має знати залежності між швидкістю, шляхом і часом, вміти використовувати формулу цієї залежності з урахуванням ситуації, розглянутої в задачі (проти течії).

Відповідь:

1. S = (Vпароплава + Vтечії річки) • t = (23,7+ 2,8) • 2,4 =

= 26,5 • 2,4 = 63,6 (км);

2. S = (Vпароплава - Vтечії річки) • t = (23,7- 2,8) • 2,4 =

= 20,9 • 2,4 = 50,16 (км). 

 

Задача 13. «Ділянка землі» [8]

Довжина одного боку земельної ділянки прямокутної форми 125 м і площа його 105000 м².

Питання 1. Чому дорівнює периметр цієї ділянки:

А) 2000                         В) 1930                       С) 1830                         D) 1950

Компетентність: 1-рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й. 

Область змісту: змінні й залежності.

Ситуація: життєва.

  Для розв’язання даного завдання учень має знати формулу площі прямокутника, вміти використовувати формулу для знаходження невідомого. 

Питання 2. Ділянку прямокутної форми необхідно загородити парканом.  Через кожні 2 м вирита яма для стовпа.  Скільки всього стовпів потрібно щоб побудувати паркан?

Компетентність: 1-й рівень – відтворення (може використовувати формули для вирішення завдань з цілими числами).

Рівень досягнення: 1-й.

Область змісту: кількість.

Ситуація: життєва.

Для розв’язання даного завдання учень повинен використовувати дані з питання 2 і виконати обчислення з цілими числами. 

Питання 3. Для осушення прямокутної ділянки землі викопали по його периметру канаву. Яка довжина канави в км, якщо сторони ділянки збільшили відповідно до 1250 м і 750 м?

Компетентність: 1-й рівень – відтворення (може використовувати формули для розв’язування завдань з цілими числами).

Рівень досягнення: 2-й.

Область змісту: змінні й залежності.

Ситуація: життєва.

Для розв’язання даного завдання учень має вміти використовувати формулу для ситуації, розглянутої в даному питанні і перетворювати одиниці вимірювання довжини в інші.

Відповідь: 1) В;  2) 965 стовп;  3) 4 км. 

 

Задача 14. «Ячмінне поле» [5]

Два ячмінних поля прямокутної форми мають площу 300000 м². 

Сторони однієї ділянки 625 м, а ширина на 225 м менше, довжина другої ділянки 400 м.

Питання 1. Чому дорівнює ширина другої ділянки?

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: залежності та зв'язки.

Ситуація: наукова.

Для розв’язання даного завдання учень повинен використовувати формулу площі прямокутника для розв’язання завдання з цілими числами. 

Питання 2. З першого поля зібрали 102,5 т ячменю, а з другого поля зібрали 16 т ячменю.  Обчисли середній урожай ячменю з одного гектара.  Відповідь округли до цілих тонн.

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: змінні й залежності.

Ситуація: життєва.

Для розв’язання даного завдання учень має знаходити середнє арифметичне чисел і володіти прийомами округлення десяткових дробів. 

Відповідь: 1) 125м;

 2) Площа першого поля 250000 м² = 25га, 102,5: 25 = 4,1 (т) - з першого поля з одного гектара, площа другого поля 50000 м² = 5 га, 16: 5 = 3,2 (т  ) – з другого поля з одного гектара.  Середній урожай: (4,1 + 3,2): 2 = 3,65 (т). З одного гектара в середньому 4 тонни. 

 

 

 

Задача 15. «Машиніст потяга» [4]

 

Згідно з розкладом, поїзд на перегоні в 720 км повинен був рухатися зі швидкістю 80 км /год

Питання 1. Знайти час у дорозі.  Формула: S = _____________

      t = ______________

Компетентність: 1-рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: змінні й залежності.

Ситуація: професійна діяльність.

Для розв’язання  даної  задачі учень повинен знати формулу залежності між величинами: швидкості, шляху, часу і вміти використовувати формулу для обчислення часу в дорозі.

Питання 2. Поїзд запізнився на 1 годину. З якою швидкістю машиніст локомотива повинен вести поїзд, щоб ліквідувати запізнення?

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при вирішенні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: змінні й залежності.

Ситуація: професійна діяльність.

Для  розв’язання даного завдання учень повинен вміти встановлювати зв'язки між даними з умов завдань при використанні стандартної формули і уявити послідовно процес вирішення завдання. 

Питання 3. Поїзд був затриманий на 1 годину після проходження ¼ шляху. З якою швидкістю машиніст повинен вести поїзд на останньому відрізку шляху, щоб прийти на кінцеву станцію без запізнення.

Компетентність: 3-го рівня – міркування (широкий спектр математичних умінь).

Рівень досягнення: 5-й.

Область змісту: змінні й залежності.

Ситуація: професійна діяльність.

Для розв’язання даного завдання учень має вміти моделювати ситуацію, зазначену в завданні, демонструвати добре розвинене мислення і вироблені навички. 

Відповідь: 1) 9 годин;  2) 90км / год; 3) 94 км / год.

 

Задача 16. «Майстерня» [5]

А) У першій майстерні майстер може виконати замовлення на виготовлення деталей за 4 години, а його учень – за 6 годин. 

Питання 1. За який час вони зможуть виконати два замовлення, працюючи спільно?

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 2-й.

Область змісту: залежності та відношення.

Ситуація: професійна діяльність.

Для розв’язання даного завдання  учень повинен знати залежності між продуктивністю праці й часом і вміти виконувати обчислення між цілими і дробовими числами. 

Б) У другій майстерні на початку робочого дня три в'язальниці отримали однакові замовлення на виготовлення серветок.  Перша з них може виконати замовлення за 8 год, друга – за 9 год, а їх учениця – за 12 год. Майстер наказав їм об'єднати замовлення і виконати всю роботу за 8 годин до кінця робочого дня. 

Питання 2. Чи встигнуть в'язальниці виконати роботу?

Компетентність: 3-й рівня – міркування (більш широкий спектр математичних умінь).

Рівень досягнення:  5-й.

Область змісту: змінні й залежності.

Ситуація: професійна діяльність.

Для розв’язання даного завдання учень має демонструвати добре вироблені навички і легко справлятися із завданням, порівняти і оцінити стратегію розв’язання завдання.

Відповідь: 1) 4,8 годин; 2) ні, так як їм потрібно працювати 9,4 год.

 

Задача 17. «Туристи» [8]

Туристи вирушили подивитися визначні пам'ятки на моторному човні.  Швидкість течії річки 2 км / год, а швидкість човна в стоячій воді 18 км / год? 

Питання 1. Туристи вирушили за течією річки і, проїхавши 1 год, повернулися назад до стоянки.  Скільки часу витратили туристи на зворотній шлях?

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язанні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: змінні й залежності.

Ситуація: особиста.

Для розв’язання даного завдання учень повинен уміти порівнювати, оцінювати;  створювати певні стратегії розв’язування проблем, що відносяться до моделі даного завдання. 

Питання 2. Туристи, відправившись на моторному човні за течією річки, повинні були повернутися назад до стоянки не пізніше ніж через 3 години.  На яку відстань можуть від'їхати туристи?

Компетентність: 3-й рівень – міркування (широкий спектр математичних умінь: математизація, математичне мислення, узагальнення, інтуїція).

Рівень досягнення: 5-й.

Область змісту: змінні й залежності.

Ситуація: особиста.

Для розв’язання даного завдання учень має вміти порівнювати, оцінювати;  створювати певні стратегії вирішення проблем, що відносяться до моделі даного завдання.

Відповідь: 1) 1,25 год; 2) не більше (26 + 2/3) км.

 

Задача 18. «Шкільна статистика» [5]

В школі відкриті класи з деяким освітніми напрямками:

Освітні напрямки	Показник (в%)
Гімназійні	12
Ліцейні	8
Художньо-естетичні	16
Санаторні	32
Загальноосвітні	32

 

Питання 1. Складіть упорядкований набір чисел. Обчисліть: середнє арифметичне, медіану, моду.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: невизначеність.

Ситуація: шкільне життя.

Відповідь: 1) 8, 12, 16, 32, 32;  2) 20;  3) 16;  4) 32.

 

Задача 19. «Чоловіче взуття» [8]

Нижче в таблиці представлено розподіл числа чоловіків за розміром використовуваного взуття:

Розмір взуття	Число чоловіків старше 16 років (% від виробленого)	Частота накопичення
До 37	1	1
38	5	6
39	12	18
40	23
41	28
42	21
43	8
44	2
і більше	-
Всього	100

 

Питання 1. Заповніть третій стовпець (частота накопичення) такої таблиці:

Розмір взуття	Число чоловіків старше 16 років (% від виробленого)	Частота накопичення
До 37	1	1
38	5	6
39	12	18
40	23
41	28
42	21
43	8
44	2
і більше	-
Всього	100

 

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й рівень.

Область змісту: невизначеність.

Ситуація: наукова.

Питання 2. Знайдіть розмір взуття, яке відповідає найбільшому відсотку чоловіків.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: невизначеність.

Ситуація: наукова.

Питання 3. Виділіть для покупки розмір взуття, яке відповідає члену частоти накопичення, що знаходиться вище середнього.

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань, поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: невизначеність.

Ситуація: наукова.

Відповідь: 1) 1, 6, 18, 41, 69, 90, 98, 100;  2) 28%, Мо = 41;  3) Ме = 41.

 

Задача 20. «Фрезерувальники» [4]

Перший фрезерувальник в день виготовляє х деталей, другий – у деталей. Застосувавши нову фрезу, перший фрезерувальник підвищив продуктивність праці на 45%, а другий – на 50,5%. 

Питання 1. Скільки деталей виготовить за день відповідно перший і другий фрезерувальники, застосовуючи нову фрезу? 

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань).

Рівень досягнення: 3-й.

Область змісту: змінні й залежності.

Ситуація: наукова.

Питання 2. Два фрезерувальники, один з яких працював 5 днів, а  інший – 8 днів виготовили 280 деталей. Застосувавши нову фрезу, перший фрезерувальник підвищив продуктивність праці на 62, 5%, а другий – на 50% і за 4 дні спільної роботи виготовили 276 деталей. Скільки деталей виготовили б вони з новою фрезою, якби, як і раніше, перший працював 5 днів, а другий – 8 днів?

Компетентність: 3-й рівень – міркування (широкий спектр математичних умінь: створення математичної моделі, математичне мислення, узагальнення, інтуїція).

Рівень досягнення: 5-й.

Область змісту: змінні й залежності.

Ситуація: професійна.

Розв’язання:

1. Перший фрезерувальник – 1,45х деталей. 

Другий фрезерувальник – 1, 505у деталей.

2. Перший етап: Складання математичної моделі задачі.

х – число деталей, виготовлених за день першим фрезерувальником зі старою фрезою, у – число деталей, виготовлених другим фрезерувальником зі старою фрезою. 

З першої умови задачі: 5х + 8у = 280. Застосовуючи нову фрезу, перший будеть виготовляти за день 1,625х деталей, а другий – 1,5 у деталей, а за 4 дні спільної роботи вони виготовлять 4(1, 625х + 1,5у)  = 6,5х + 6у деталей. 

З другої умови: 6,5х + 6у = 276.

Математична модель ситуації, описаної в даному питанні:

Другий етап: Робота з складеної моделлю.

Розв’язуючи систему рівнянь, знаходимо:

х = 24, у = 20.

Третій етап: Відповідь на питання завдання (переклад мови математики на мову завдання). 

Перший фрезерувальник зі старою фрезою за день виготовляв 24 деталей, а новою: 1,625 • 24 = 39 (деталей).

 Другий фрезерувальник зі старою фрезою за день виготовляв 20 деталей, а нової: 1,5 • 20 = 30 (деталей). 

Якщо перший працює 5 днів, а другий –  8 днів, то вони виготовлять

 5 • 39 + 88 • 30 = 435 (деталей).

 Відповідь: 435 деталей.

 

Задача 21. «Новини телеканалів» [5]

У таблиці зібрана інформація про  виході новин на чотирьох телеканалах

Канали	1-й випуск	2-й випуск і далі
Канал №1 (республіканський)	6-00	9-00 і далі через кожні 3 години
Канал №2 (республіканський)	8-00	11-00 і далі через кожні  3  години
Канал №3 (обласний)	6-00	10-00 і далі через кожні 4 години
Канал №4 (міський)	9-30	11-30 і далі через кожні 2 години

 

 Питання 1. Виберіть дерево з можливих варіантів вибору, яке відповідає  періоду з 18-00 до 23-45годин:

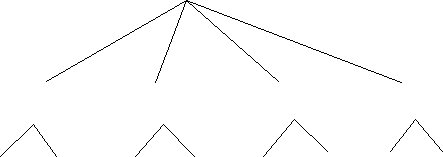А

 

 

ТВ-канал                  №1                     №2                      №3                      №4 

 

 

Новини          6-00      9-00         8-00     11-00     6-00      10-00    9-30     11-30

 

 

 

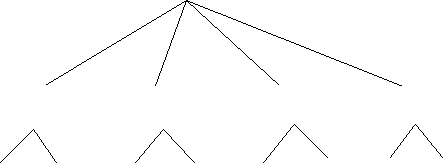В

 

 

ТВ-канал           №1                     №2                      №3                      №4 

 

 

Новини  18-00      21-00  20-00       23-00    18-00     22-00    19-00   21-30  23-30

 

 

 

 

С

 

 

 

ТВ-канал                 №1                     №2                        №3                      №4 

 

Новини     6-00          9-00     19-00   21-30  23-30    8-00     10-00   18-00    22-00   

 

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань).

Рівень  досягнення: 4-й.

Область змісту: змінні й відношення.

Ситуація: інформаційна.

Відповідь: 1) В.

 

 

 

Задача 22. «Контрольна робота» [4]

Вчителька підготувала до контрольної роботи чотири завдання на розв’язування лінійних нерівностей, п'ять текстових завдань (дві на рух і три на роботу) і шість завдань на розв’язування квадратних рівнянь (в двох завданнях дискримінант від’ємний). У контрольній має бути по одному завданню на кожну з трьох тем. 

Питання 1. Яка загальна кількість всіх можливих варіантів контрольної роботи? 

А) 20                      В) 24                    С) 30                             D) 120     

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: кількість.

Ситуація: професійно-методична.

Питання 2. Яка загальна кількість всіх можливих варіантів, у яких зустрінеться завдання на рух?

 А) 120                       В) 72                    С) 48                       D) 18

 Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: невизначеність.

Ситуація: професійно-методична.

Питання 3. Яка загальна кількість всіх можливих варіантів, у яких у квадратного рівняння буде хоча б один корінь? 

А) 80                          В) 120                       С) 48                           D) 56

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: невизначеність.

Ситуація: професійно-методична.

Питання 4. Яка загальна кількість усіх можливих варіантів, у яких не зустрінуться одночасно завдання на роботу і квадратне рівняння? 

Компетентність: 3-й рівень – міркування.

Рівень досягнення: 5-й.

Область змісту: невизначеність.

Ситуація: професійно-методична.

Відповідь:

1) D;  2) С;  3) А; 

4) Із загальної кількості варіантів ми віднімемо ті варіанти, в яких зустрінуться одночасно і завдання на роботу, і квадратне рівняння, що не має кореня. У порівнянні з аналогічним запитанням 1), для них змінюється число випадків при виборі текстової задачі (3 варіанти) і число випадків при виборі рівняння: тільки в двох випадках коренів немає.

Значить, таких контрольних можна скласти 4 • 3 • 2 = 24, а кількість, що є відповіддю на питання завдання становить 120-24 = 96.

Відповідь: 96.

 

 

 

 

 

Задача 23. «Урок» [4]

 Після уроків з теми «Статистика» на дошці залишилася таблиця:

Варіанта	4	7
Кратність	5	2	3

І відповідь: «Середнє значення = 10». 

Питання 1. Заповніть порожнє місце в таблиці.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 2-й.

Область змісту: невизначеність.

Ситуація: шкільне життя.

Питання 2. Вказати розмах і моду розподілу.

Компетентність: 1-й рівень – відтворення (простих математичних дій, прийомів, процедур).

Рівень досягнення: 1-й.

Область змісту: невизначеність.

Ситуація: шкільне життя.

Питання 3. Кожен член заданого ряду – ціле число.  Чи може у відповіді для середнього значення стояти число 15? «Так» / »НІ». Відповідь обґрунтуйте.

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань, поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: невизначеність.

Ситуація: шкільне життя.

Питання 4. Заповніть порожнє місце в таблиці, якщо у відповіді для середнього значення стоїть число х.

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 3-й.

Область змісту: невизначеність.

Ситуація: наукова.

Розв’язання:

1. Нехай в порожній клітці стоїть число а. 

За визначенням середнього значення отримаємо:

100 = 20 + 14 + 3а → 66а = 3а → а = 22.

Відповідь: 22.

2) Розмах: 22-4 = 18, Мода: 4.

3) Розв’яжемо  рівняння

а – не ціле число, отже, відповідь «Ні».

4) Розв’яжемо рівняння щодо а:

 

Задача 24. «Собівартість» [8]

У таблиці наведено собівартість одного квадратного метра  стіни з газоблоку товщиною 200 мм з утепленням мін. плити товщиною 140 мм і одного квадратного метра таркетованої і заштукатуреної по обидва боки стінової плити з армованого пінополістиролу товщиною 150 мм. 

Технологія приготування стін	Вартість матеріалів
Газоблок «Экотон» + мін.плита
Газоблок «Экотон» 1 м3	15000 тенге
Мін.плита «URSA» 1 м3	18000 тенге
Робота каменярі 1 м3	5500 тенге
Клей кафельний на  1 м 3 кладки	2200 тенге
Термопанель «Impac» товщ. 150 мм
Термопанель «Impac» 150 мм	27 $ США ≈ 4050 тенге  (курс 1$США = 150 тенге)
Ц/п розчин 1 м³(М200)	10000 тенге
Закладні (Ø8 и Ø10)	300 тенге
Робота: Монтаж термопанелі 1 м²	150 тенге
ц/п штукатурка 1 м³(з 2-х сторін)	1200 тенге

 

Примітка: У розрахунку не враховується швидкість роботи, а також використання механізації, кількість робочих. 

Питання 1. Знайдіть вартість стіни за 1 м² при використанні технології «Газоблок« Екотон » + мін. плити» (1-ша технологія).

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів і міркувань).

Рівень досягнення: 2-й.

Область змісту: кількість.

Ситуація: наукова.

Питання 2. Знайдіть вартість стіни за 1 м² при використанні технології «Термопанель «Impac» (армована пінополістирол)» (2-га технологія).

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів та міркувань).

Рівень досягнення: 2-й.

Область змісту: кількість.

Ситуація: наукова.

Питання 3. Яка з  технологій є економічною? Підкресліть. Перша технологія: так / ні. Друга технологія: так / ні. Скільки відсотків становить економія?

Компетентність: 2-й рівень – встановлення зв'язків (між даними з умов завдання, при розв’язуванні стандартних завдань і поясненні процесів та міркувань).

Рівень досягнення: 3-й.

Область змісту: кількість.

Ситуація: наукова.

Відповідь:

1. Вартість стіни за 1 м²:

(15000 + 2200) ˟ 0,2 + (18000˟0,14) + (5500˟0,2) = 7060 тенге.

2. Вартість стіни за 1 м²:

4050+(10000˟0,06)+300+150+1200 = 6300 тенге.

3. Перша система охолодження: так / ні.

Друга система охолодження так / ні.

Близько 11-12%. 

Задача 25. «Дача» [8]

Марат вирішив провести ремонт дачного будиночка.  Необхідно обклеїти стіни шпалерами і пофарбувати підлогу.  Розміри стін в кімнаті 3˟4˟2,5м, вікно – 2 м², двері – 2 м². 

Питання 1. Чому дорівнює площа підлоги?

Компетентність: 1-й рівень – відтворення.

Рівень досягнень: 2-й.

Область змісту: кількість.

Ситуація: особисте життя.

Питання 2. Скільки рулонів шпалер треба купити, якщо рулон шпалер має ширину 60см і довжину 10м?

Компетентність: 2-й рівень – встановлення зв'язків.

Рівень досягнення: 3-й.

Область змісту: кількість.

Ситуація: особисте життя.

Питання 3. Скільки банок фарби масою 1 кг потрібно купити в магазині, якщо витрата фарби на 1м² становить 150г.

Компетентність: 1- й рівень – відтворення.

Рівень досягнення: 2-й.

Область змісту: кількість.

Ситуація: особисте життя.

Відповідь: 1) 12 м²;  2) 6 рулонів; 3) 2 банки фарби.

 

 

Задача  26. «Купа щебеню» [4]

 

 Ви – керівник підприємства.  Постачальник пропонує вам за подібною ціною купу щебеню, називаючи її обсяг 900 м³.  Проведено наступні вимірювання: відстань від підніжжя гори до вершини – 13м, довжина кола основи – 72м. 

Питання 1. Яка висота H купи? 

Питання 2. Чи погодитеся ви з пропозицією постачальника, якщо ваше підприємство допускає в таких ситуаціях збитки не більше 3%?  Так / Ні.

Розв’язання:

1. Купа щебеню – конус.  Основа С = 2ПR;  R = C / 2П;

R = 72: 6 = 12м; L² = H²+R², H² = 169-144 = 25, H = 5м.

Відповідь: 5м.

2) V = 1/3ПR²H; V = 1/3 ˟ 3 ˟ 144 ˟ 5 = 720м³;

720 ˟ 0,03 = 21,6 720 + 21,6 = 741,6 м³. Щебеню менше.

Відповідь: НІ – не погоджуся.

 

Задача 27. «Поле» [5]

Селянське господарство відвело два поля під «зеленку» (овес з горохом) для заготівлі силосу на зиму. Одне поле площею 25,5 га, інше – в 1,5 рази більше. 

Питання 1: Скільки треба придбати насіння при нормі висіву 200 кг на один гектар?

Компетентність: 2-й рівень – встановлення зв'язків.

Рівень досягнень: 3-й.

Область змісту: кількість.

Ситуація: наукова.

Відповідь: 1) 12750 кг.

 

Задача 28. «Клумба» [10]

 

У дворі Марата є клумба, що має форму кола з діаметром 3м. 

Питання 1: Чому дорівнює довжина бордюру, що вимагається для огорожі клумби?  Відповідь округлити до десятих. 

А) 9,4                 B) 9                     C) 9,2                      D) 9,1

Компетентність: 1-й рівень – відтворення.

Рівень досягнень: 1-й.

Область змісту: кількість.

Ситуація: наукова.

Відповідь: 1) А.

 

 

 

 

 

 

 

 

 

 

 

Висновки

 

 В даній роботі розглянуто деякі особливості тестування PISA, з  математики зокрема.

Завдання PISA побудовані так, щоб перевірити уміння школярів вирішувати цілком реальні життєві ситуації.

Тести PISA покликані з'ясувати, наскільки людина володіє здатністю використати знання для вирішення суто практичних завдань. Більше того, завдання цього дослідження спеціально побудовані так, щоб перевірити уміння школярів вирішувати цілком реальні життєві ситуації.

 Одним з шляхів вирішення протиріччя між якістю навчання що 15-річних учнів і результатами міжнародного дослідження PISA є відповідна методична система навчання, ґрунтована на фундаментальних математичних знаннях і орієнтована на деякі "мета-уміння", уміння самостійно добувати нову для себе інформацію, освоювати нові види діяльності, сприяючі саморозвитку і самоосвіті.

 Підготовку до дослідження PISA в Україні розпочато. У межах Українського центру оцінювання якості освіти (УЦОЯО) створено Центр PISA. Його фахівці отримали від Міжнародного консорціуму тестові завдання, переклали їх, потім зібрали фахову комісію, фахівці якої проаналізували і надали свої рекомендації.  [7]

 Вважається, що це дослідження буде корисне не лише отриманими даними. Воно стане корисним й для вчителів, які побачать завдання іншого типу і для учнів. 

 Результати України в PISA-2018 можна очікувати в грудні 2019-го. 

Бібліографія

1.         PISA. Програма міжнародного оцінювання учнів. Український центр оцінювання якості освіти. – К., 2016. – 36 с.
2.         Бобак Н. В., Мартинюк О. В., Марочко Н. М. Моніторинг якості освіти: міжнародний досвід. – [Електронний ресурс] – режим доступу – http://www.ippo.if.ua/files/ІМ/MON/Bobak.pdf.
3.         Ломакович С. В. , Панченков А. О., Терещенко В. М. Участь у проекті PISA як потенційна можливість побачити вітчизняну освіту без «прикрас» / Вісник. Тестування і моніторинг в освіті. – 2015. № 11 – 12. – С.19 – 23.
4.         Методика конструирования тестовых заданий по математике в контексте с международными исследованиями PISA. Методическое пособие/ Кагазбаева А.К. – Актобе: ред.-изд.отдел филиала АО НЦПК «Өрлеу», 2015 – 120 с.
5.         Полат Е.С. Новые педагогические и информационные технологии в системе образования: Учебное пособие. – М.: Академия, 2003. – 272 с.
6.         Програма PISA (програма міжнародного оцінювання учнів) / Вісник. Тестування і моніторинг в освіті. – 2011. № 11 – 12. – С.39 – 68.
7.         Україна з 2018 року приєднається до міжнародної оцінки знань PISA // Незалежне бюро новин, 9.11.2015. – [Електронний ресурс] – режим доступу – http://nbnews.com.ua/ua/news/165426/.
8.         Ковалева Г.С., Краснянская К.А. Примеры заданий по математике. Центр оценки качества образования ИСМО РАО. – М: 2006 – 42 с.

Інтернет-ресурси

9.         ://zn.i./ei//.
10.    http://pisa.testportal.gov.ua/math1.