Методика розв'язання задач з теми "Чотирикутники"
Методика розв’язування окремих типів задач
Задачі на обчислення
Задача на обчислення з числовими даними є окремим випадком задачі з параметричними даними, тому часто виникає потреба розглядати саме їх.
Починаючи розв’язувати геометричну задачу на обчислення, щоразу необхідно враховувати особливості конфігурації, описаної в умові задачі. Зазвичай це складне завдання, яке вимагає високої культури обчислень і розуміння суті знайдених залежностей. Наведемо приклад.
Задача 1. У трикутник вписано паралелограм зі сторонами 3 і 5 см і діагоналлю, що дорівнює 6 см. Знайти сторони трикутника, якщо відомо, що діагоналі паралелограма паралельні бічним сторонам трикутника, а менша з його сторін лежить на основі трикутника.
Розв’язання DFGH – паралелограм(рис. 53), вписаний у ![]() ABC зазначеним способом HG=3см, DH=5cм. Нехай d1 і d2 - діагоналі паралелограма.
ABC зазначеним способом HG=3см, DH=5cм. Нехай d1 і d2 - діагоналі паралелограма. ![]()
Рисунок 53
Тоді
![]()
Оскільки d2![]() d1, то d2= HF діагональ, що лежить проти гострого кута, а
d1, то d2= HF діагональ, що лежить проти гострого кута, а
Діагональ, що лежить проти тупого кута. Оскільки DFHC і DFBG – паралелограми (мають дві пари паралельних сторін), то
CH=GB=DF=3, а значить CB=3+3+3=9см.
Маємо FB=DG=6; CD=HF=![]()
ADOF – також паралелограм, AF=DO=![]() DG=
DG=![]() і AB=AF+FB=3+6=9см.
і AB=AF+FB=3+6=9см.
тоді AD=OF=![]() HF=
HF=![]() і AC=AD+DC=
і AC=AD+DC=![]()
Відповідь 9см, 9 см, ![]()
Задача на обчислення з числовими даними є окремим випадком задачі з параметричними даними, тому часто виникає потреба розглядати саме їх.
Задача 2. У квадрат вписано другий квадрат, вершини якого лежать на сторонах першого, а сторони утворюють зі сторонами першого кути в 600. Яку частину площі даного квадрата становить площа вписаного?
Розв’язання
Квадрат EFGH вписано у квадрат ABCD зазначеним способом. (Рис.54)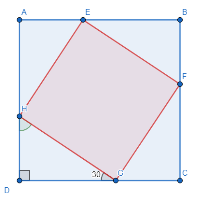
Рисунок 54
Позначимо EF=a. Тобто DC=DE+EC=![]() . Маємо
. Маємо
![]() =
=![]()
Відповідь: ![]()
Задачі на доведення
Задача на доведення в курсі геометрії виражає собою вимогу обгрунтувати конкретне математичне твердження, яке визначено в її умові. Розв’язком геометричної задачі на доведення є виведене твердження задачі з аксіом та раніше доведених теорем або наслідків з них. В курсі геомерії задачі на доведення бувають двох видів: а) такі, під час розв’язування яких допускають, що описані в їх умовах геометричні фігури існують; б) такі, в яких факт існування геометричної фігури, про яку йдеться в задачі, треба довести.
Задачі першого виду вважаються розв’язаними, коли, виходячи з умови, обґрунтовується її висновок. При цьому переформування умови зазвичай є засобом знаходження розв’язку задачі, оскільки дає можливість розв'язати іншу задачу, розв’язання якої є простішим, або відомим.
У ході розв’язування задач на доведення часто виникає потреба дослідити існування математичного об’єкта, описаного її умовою. Результати такого дослідження можуть суттєво впливати як на хід розв’язування задачі, так і на вираз у відповіді.
Задача. [7] Доведіть, що точка перетину бісектриси кутів, прилеглих до бічної сторони трапеції, належить прямій, яка містить її середню лінію.
![]()
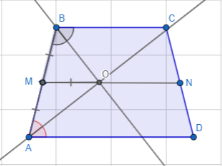
Розв’язання Нехай ABCD – трапеція, BC ǁAD. BO і AO –бісектриси, т.О –точка перетину бісектрис, MN – середня лінія трапеції ABCD. Доведемо, що т.О є MN. За властивістю бісектрис трапеції, ПРОВЕДЕНИХ з бічних кутів при бічних сторонах, перетинаються під прямим кутом (∠AOB =900) .
Проведемо медіану з DM. За властивістю медіани, проведеної з вершини прямого кута до гіпотенузи. ![]() Так як OM=BM, то ∆OMB- рівнобедрений з основою BO, тоді ∠BOM=∠MBO; ∠MBO=∠OBC. А так як ці кути є внутрішніми різносторонніми при OMǁBC і січною BC. Таким чином пряма OMǁBC (основа трапеції) і проходить через середину бічної сторонни AB. Отже, т.О лежить на середній лінії трапеції. Доведено.
Так як OM=BM, то ∆OMB- рівнобедрений з основою BO, тоді ∠BOM=∠MBO; ∠MBO=∠OBC. А так як ці кути є внутрішніми різносторонніми при OMǁBC і січною BC. Таким чином пряма OMǁBC (основа трапеції) і проходить через середину бічної сторонни AB. Отже, т.О лежить на середній лінії трапеції. Доведено.
[17]Задача Доведіть, що навколо прямокутника можна описати коло
-
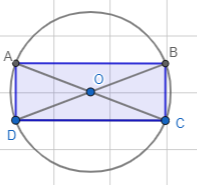 Нехай задано прямокутник ABCD, O-точка перетину його діагоналей.
Нехай задано прямокутник ABCD, O-точка перетину його діагоналей.
- Оскільки OA=OB=OC=OD, то коло центром якого є точка O, з радіусом OA буде проходити через всі вершини прямокутника, а тому буде описаним навколо прямокутника.
-
 Отже, навколо прямокутника можна описати коло, що й треба було довести.
Отже, навколо прямокутника можна описати коло, що й треба було довести.
Задачі на побудову
Розв’язання задачі на побудову здійснюється за таким алгоритмом:
1) аналіз; 2) побудова; 3) доведення; 4) дослідження.
Аналіз - це пошук способу розв’язання задачі на основі взаємозв’язків єдності аналізу та синтезу. Під час аналізу виконують план розв’язання задачі. Виконуючи план розв’язання задачі рекомендовано , щоб він базувався необхідних умовах, а саме на тих властивостях, які випливають безпосередньо з існування розв’язання. За таким планом можна здійснити дослідження задачі.
Побудова здійснюється відносно плану за допомогою вказаних елементів. Цей етап теоретично можна виконати, а ось при практичному виконанні треба врахувати вибір величин даних в умові кутів та відрізків.
Доведення це зазвичай усвідомлення та перевірка правильності.
При виконанні дослідження визначається за яких саме умов задача не буде мати розв’язків, а якщо буде мати то скільки.
Дотримання етапів розв'язування задач на побудову робить міркування учнів більш цілеспрямованими і логічно послідовними, привчає до повноти розв'язування будь-яких математичних задач. Проте не слід прагнути проводити їх у кожній задачі на побудову. В одній задачі заслуговує на увагу аналіз, у другій - цікава сама побудова, у третій - повчальним є доведення або дослідження
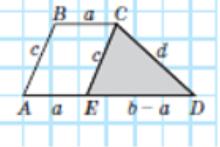 Задача [7] Побудуйте трапецію за чотирма сторонами.
Задача [7] Побудуйте трапецію за чотирма сторонами.
Розв’язання
Нехай а іb (a<b) – основи шуканої трапеції,c і b – її бічні сторони.
Аналіз
![]() Нехай шукану трапецію ABCDпобудовано (рис. 57) Проведемо через вершину С пряму СЕ, паралельну АВ. Тоді ABCE - паралелограм за означенням, отже, CE=AB=c. Крім того, AE=BC=a,отже, ED=b-a.
Нехай шукану трапецію ABCDпобудовано (рис. 57) Проведемо через вершину С пряму СЕ, паралельну АВ. Тоді ABCE - паралелограм за означенням, отже, CE=AB=c. Крім того, AE=BC=a,отже, ED=b-a.
Допоміжний трикутник ECDможна побудувати за трьома сторонами. Після цього для отримання вершин A i B треба відкласти на промені DE і на промені з початком C, паралельному DE, відрізки завдовжки a.
Побудова
- Побудуємо відрізок b-a.
- Побудуємо трикутник ECD за трьома сторонами (ED=c, CD=d, ED=b-a).
- Побудуємо промінь, який проходить через точку С і паралельний DE. При цьому побудований прoмінь DE мають лежати по один бік від прямої CD.
- На промені DEвід точки E відкладаємо відрізок EA=a, на промені з початком С - відрізок СВ=а
- Сполучимо точки А і В.
Доведення
За побудовою BC‖AD, BC=AE=а, отже ABCE-паралелограм за ознакою. Звідси AB = CE =c.Крім того, AD=a+b-a=b, CD=d. Отже, ABCD -шукана трапеція
Дослідження
Задача має єдиний розв’язок, якщо числа b-a, с і d задовольняють теорему про нерівність трикутника.
Задача.[6] Побудуйте паралелограм за двома діагоналями і кутом між ними.
Розв’язання
Нехай d1і d2 – дані діагоналі паралелограма, α – кут між ними.
Аналіз
Нехай паралелограм ABCD побудовано (рис. 58)
Трикутник AOBможна побудувати за двома сторонами і кутом між ними (AO=![]() α)Таким чином, ми отримаємо вершини AO i BO.
α)Таким чином, ми отримаємо вершини AO i BO.
![]()
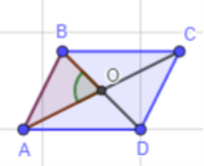 Побудова
Побудова
1. Розділимо відрізки d1 і d2 навпіл.
2. Побудуємо трикутник AOB за двома сторонами і кутом між ними.
3. На променях AO і BO відкладемо відрізки OC = AO і OD = BO.
4. Послідовно сполучимо точки B, C, D і A.
Доведення
ЧотирикутникABCD – паралелограм, оскільки за побудовою його діагоналей AC i BCточкою перетину діляться навпіл. У цьому паралелограмі∠AOB=α(за побудовою).
AC=![]() BD=
BD=![]()
Дослідження
Задача має єдиний розв’язок за будь-яких значень ![]() ,
, ![]() .
.
Задачі на дослідження
Задача. Чи вистачить 40 см дроту, щоб виготовити з нього паралелограм зі сторонами 14см і 8см.
Розв’язання
Для розв’язання цієї задачі учні мають практично застосувати формулу знаходження периметра паралелограма. І виконати обчислення.
а=14см, b=8см. Р=(a+b)∙2=(14+8)∙2=44cм.
44см>40см, тому 40 см дроту не вистачить.
Задача.[6] Квадрат і ромб мають рівні периметри. Дослідити площа якої фігури більша?
Оскільки учень буде мати справу з площами квадрата і ромба то доцільно записати формули. Площа квадрата S=a2, площа ромба S=a∙ha , де ha це висота ромба, а з іншої сторони це катет прямокутного трикутника з гіпотенузою а , тобто h < а . Провівши відповідне дослідження учень мав би сказати, що площа квадрата більша за площу ромба. Дослідження полягає у тому, що добуток висоти на сторону буде меншим за квадрат цієї сторони.
2.2 Задачі за готовими малюнками на уроках планіметрії
Від активності старшокласників у процесі пізнавальної діяльності під час вивчення шкільного курсу геометрії залежать результати їх знань, формування вміння діяти творчо, а також, у майбутньому, готовність виконувати професійну діяльність уже в нових життєвих умовах. [5]
У практиці навчання планіметрії спостерігається зростання інтересу учнів до розв‘язання задач, умову яких вони можуть одразу побачити на вже готових малюнках [14]. Часто, створивши рисунок за умовою задачі, учень не вміє його опрацювати – виділяти зорово необхідну частину задачі і залишати поза увагою інші елементи на зображенні, виконувати допоміжні позначення на рисунку. Тому такі вміння треба формувати в учнів протягом вивчення всього курсу планіметрії. Застосування задач за готовими малюнками допомагає краще організувати діяльність учнів на уроці, забезпечити активну самостійну діяльність старшокласників, може бути засобом контролю й самоконтролю знань, умінь, а також дозволяє значно економити навчальний час. [15]
Учитель може урізноманітнювати методики навчання. Наприклад, розпочинати розв’язування задач по новій темі із готових малюнків або ж демонструвати малюнок на відкидній дошці на екрані уже після того, як учні самі зробили потрібні зображення у своїх зошитах. Розв’язування задач бажано проводити письмово. Рисунок можна не копіювати , якщо цього не вимагається.
Можна підбирати такі задачі, коли один рисунок буде супроводжувати декілька завдань.
У курсі планіметрії за допомогою усних вправ на готових кресленнях вирішуються такі дидактичні завдання:
- Засвоєння теоретичних знань із поточного матеріалу.
- Формування навичок практичного застосовування відповідних теорем до розв'язування задач.
- Узагальнення і систематизація базових геометричних знань та вмінь .
- Організація самостійного розв'язування задач.
- Розвиток математичної мови учнів [16].
Для прикладу, під час вивчення теми «Паралелограм» для усного колективного розв’язування на уроці або для проведення перевірочної самостійної чи контрольної роботи можна використати завдання всіх рівнів складності, позначені зірочками, для яких умова одна, а малюнки різні:
![]()
Використання завдань за готовими малюнками дозволяє істотно збільшити кількість задач, розв’язаних на уроці, розглянути різні типи задач по темі(рис.58) [15].
2.3 Задача одного уроку
Розв‘язування задач різними способами дає змогу:
- активізувати пізнавальну діяльність учнів;
- розвивати гнучкість мислення та здатність прогнозувати;
- обрати найраціональніший спосіб розв‘язання;
- перевірити правильність розв‘язання даної задачі;
- сприяти мобілізації всіх знань учнів, виявленню винахідливості й оригінальності мислення;
- систематизувати й узагальнити навчальний матеріал, установити міжпредметні зв‘язки;
- отримати моральне задоволення учневі, який знайшов інший спосіб розв‘язання задачі
Розв‘язування задач різними способами формує в дітей звичку самостійно висувати гіпотези і перевіряти їх, порівнювати отримані результати, доходити висновків, а головне, вона вчить мислити логічно та критично.[11]
Проводити урок одніє задачі доцільно, коли учні вже навчилися використовувати кожну із запропонованих теорем чи ознак. Це сприяє систематизації знань та умінь, набутих на попередніх уроках, глибшого дослідження властивостей геометричних фігур.
Коли учні навчилися використовувати кожну із запропонованих теорем та ознак, варто, для систематизація знань та умінь, представити задачі, які можна розв‘язати кількома способами, використовуючи набуті знання.[4]
Задача. На сторонах AB I AD квадрат ABCD позначили точки K і M відповідно так, що AK +Am=AB. Знайти ∠KOM, де О- центр квадрата.
1 спосіб:
![]()
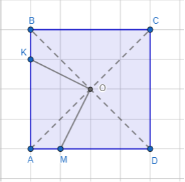 AK+AM=AB; KB=AB-AK;
AK+AM=AB; KB=AB-AK;
AK+KB=AB; KB=AB-AK
Оскільки AB-AK= AB-AK то AM=KB (рис.59)
- Розглянемо ΔKOB і ΔMAO: ΔKOB= ΔMOA за двома сторонами AM=KB, AO=OB і кутом між ними ∠KBO=∠MAO.
- Розглянемо чотирикутник KOMA. Нехай ∠KBO=∠MAO=α, тоді ∠AKO=∠AMO=1800-α(як суміжні кути), а ∠KAM=900: отже, ∠KOM=3600-1800+α-α-900.
2 спосіб
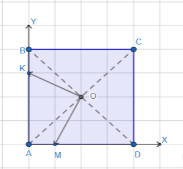 Виберемо систему координат так, що дві сторони квадрата лежать на осях абсцис і ординат(рис. 60) Нехай сторона квадрата дорівнює а см, тоді
Виберемо систему координат так, що дві сторони квадрата лежать на осях абсцис і ординат(рис. 60) Нехай сторона квадрата дорівнює а см, тоді
A(0;0), B(0;x), M(m;0), O(![]() , D(a;0)K(0,a)
, D(a;0)K(0,a)
![]() Тоді
Тоді ![]()
![]()
Отже, OK⊥OM⇒∠KOM=900
Відповідь: 900


про публікацію авторської розробки
Додати розробку
