Методика вивчення арифметичної та геометричної прогресії у 9 класі

БЕРЕСЬКА ГІМНАЗІЯ ДОРОСИНІВСЬКОЇ СІЛЬСЬКОЇ РАДИ ВОЛИНСЬКОЇ ОБЛАСТІ

 

 

 

Юлія Мазелюк

 

 

Методика вивчення арифметичної та геометричної прогресії у 9 класі

 

(методичні рекомендації)

 

 

 

 

 

 

Доросині -2022

Мазелюк Юлія Анатоліївна, вчитель математики. «Методика вивчення арифметичної та геометричної прогресії у 9 класі» (методичні рекомендації). –Береська гімназії Доросинівської сільської ради, 2022. – 29с.

 

    Визначне місце при вивченні алгебри у 9 класі має тема «Арифметична та геометрична прогресія».

          В даній роботі сформульовано означення арифметичної та геометричної прогресія; розглянуті зв’язки прогресії з біологією, фізикою, економікою; наведені приклади задач пов’язаних з  прогресіями та методика їх розв’язування.

 

Видання розраховане для вчителів математики при викладанні алгебри у 9 класі, а також для позакласної роботи.

 

 

 

 

 

 

 

 

 

Рецензенти:

 Дацюк Н. М.- заступник директора з навчально-виховної роботи Береської гімназії Доросинівської сільської ради

Рощук Н.В. – директор гімназії Доросинівської сільської ради

 

Схвалено  педагогічною радою

Береської гімназії Доросинівської сільської ради

(протокол № 8 від 14 лютого  2022 року)

ЗМІСТ

прогресія арифметичний геометричний алгебра

Вступ ……………………………………………………………………………...4

Розділ 1. Теоретичні основи ……………………………………………………6

1.1.Історія виникнення арифметичної та геометричної прогресії……….6

1.2 Арифметична та геометрична прогресії та основні поняття пов’язані з ними …………………………………………………………………………….8

1.3 Методика вивчення формул n-го члена та формул суми перших членів арифметичної та геометричної прогресії …………………………..12

1.4. Прогресії та їх практичне застосування ……………………………..16

Розділ 2. Задачі пов’язані з прогресіями та методика навчання їх розв’язання ……………………………………………………………………..17

2.1. Методика навчання учнів розв’язання задач пов’язаних арифметичною прогресією …………………………………………………17

2.1.1. Задачі на знаходження членів арифметичної прогресії, використовуючи формулу n-го члена і властивості арифметичної прогресії. ………………………………………………………………………17

2.1.2. Задачі на відшукання суми перших послідовних n членів арифметичної прогресії ………………………………………………………19

2.1.3. Прикладні задачі пов’язані з арифметичною прогресію…………21

2.2. Методика навчання учнів геометричної прогресії……………………23

2.2.1 Задачі на знаходження членів геометричної прогресії, використовуючи формулу n-го члена і властивості геометричної прогресії……………………………………………………………………….23

2.2.2 Задачі на відшукання суми n перших членів геометричної прогресії………………………………………………………………………..24

2.2.3 Задачі на відшукання суми нескінченно спадної геометричної прогресії …………………………………………………………………………25

Висновки………………………………………………………………………27

Список використаної літератури ……………………………………………28

Вступ

 

Одним з актуальних завдань, що стоять перед сучасною шкільною математичною освітою, є формування інтелектуального потенціалу учнів, розвиток їхніх пізнавальних інтересів і творчої активності. Матеріал, пов'язаний з прогресіями, починає вивчатися в 9 класі в шкільному курсі алгебри. У школі арифметичним і геометричним прогресіям приділяється досить мало уваги. Актуальність даної теми полягає в широкому використанні прогресій при дослідженнях в таких науках як економіка, фізика, проектування, біологія. Розв’язуючи задачі з біології, фізики, економіки можна використати властивості і формули арифметичних та геометричних прогресій, що приведе, іноді, до єдиного вірного шляху розв’язування цих задач.

Об’єкт дослідження – процес навчання курсу алгебри 9 класу.

Предметом дослідження є арифметична і геометрична прогресії та їх властивості.

Метою даної роботи є: на основі опрацьованої навчально–методичної літератури систематизувати теоретичні відомості про арифметичну та геометричну прогресії та їх властивості, розробити ефективну методику навчання учнів розв’язування задач пов’язаних з арифметичною та геометричною прогресією під час навчання курсу алгебри 9 класу.

Завдання  роботи:

1) провести аналіз проблеми дослідження в навчально – методичній літературі.

2) розглянути методику навчання теоретичних питань пов’язаних з арифметичною та геометричною прогресіями

3) підібрати диференційовану систему задач пов’язаних з арифметичною та геометричною прогресіями

4) розробити методику навчання учнів розв’язування задач запропонованої в роботі системи.

Робота складається з двох розділів. Перший розділ - присвячений загальним відомостям про арифметичні та геометричні прогресії та їх практичне застосування. У другому розділі наведена методика навчання учнів розв’язування задач пов’язаних з арифметичною та геометричною прогресіями різних рівнів складності.

 

Розділ 1. Теоретичні основи

1.           Історія виникнення арифметичної та геометричної прогресії.

Числові послідовності – явище  унікальне. Історія їх виникнення губиться в глибині віків. Вже у клинописних табличках вавилонян, у єгипетських папірусах, датованих ІІ тисячоліттям до н.е., зустрічаються задачі на арифметичну і геометричну прогресії. Впродовж століть людей приваблювала внутрішня гармонія і краса числових рядів.

На зв’язок між прогресіями першим звернув  увагу великий АРХІМЕД (бл. 287 -212рр. До н.е.)

Слово “прогресія” походить від латинського слова “progression” і означає “ рух уперед”. Уперше цей термін як математичний вживається у працях римського вченого Боеція (V - VIст).

Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е.

Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса: “Нехай тобі сказали: розділи десять мір ячменю між 10 чоловіками так, щоб різниця між кожним чоловіком і його сусідом становила 1/8 міри ячменю”.          

В XVIII ст. в англійських підручниках з’явилися позначення арифметичної і геометричної прогресії.

Коли німецькому математику К.Ф. Гауссу було 9 років, учитель, прагнучи надовго зайняти дітей, задав на уроці наступну задачу: “порахувати суму всіх натуральних чисел від 1 до 100”. Але один із учнів ( це був Гаусс) через хвилину викрикнув: ”Я вже розв’язав”. У  зошиті Гаусса було тільки одне число, але зате вірне.

Помітивши, що суми 1+100, 2+99 і т. д. рівні, він помножив 101 на 50, тобто 1+2+3+4+…+98+99+100=101∙50=5050. Інакше кажучи, він помітив закономірність, яка властива арифметичній прогресії. К. Гаусс знайшов суми членів арифметичної прогресії.

Ось іще одна дуже відома задача з того ж папірусу:  «У семи людей по сім кицьок; кожна кицька з'їдає по сім мишей, кожна миша з'їдає по сім колосків, з кожного колоска може вирости по сім мір ячменю. На  скільки великі числа цього ряду та їх сума?»

 

       Ця ж задача багато разів з різними варіаціями повторювалась і у інших народів в інші часи. Наприклад, у книзі XIII ст. «Книга абакa» Леонардо Пізанського(Фібоначчи) є задача, в якій фігурують 7 старух, що направились до Риму (імовірно, паломниць), у кожної з яких 7 мулів, на кожному з яких по 7 мішків, і в кожному з яких по 7 хлібів, в кожному з яких по 7 ножів, і кожен з яких в 7 ножнах. В задачі питають, скільки всього предметів.

  Дослідники стверджують, давні вавілоняни також добре були знайомі з обома прогресіями.

 

 

 

 

 

1.2. Арифметична та геометрична прогресії та основні поняття пов’язані з ними

Арифметичною прогресією називають послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називають різницею арифметичної прогресі.

Введення властивостей арифметичної прогресії найзучніше показати на конкретних прикладах, а потім записати в загальному вигляді.

Наприклад, в арифметичній прогресії 1; 3; 5; 7; 9; ... кожний член, починаючи з другого, є середнім арифметичним двох сусідніх з ним членів:

 

3 ₌ ;             5 ₌ ;           7 ₌ ;

 

Покажемо, що таку властивість має будь-яка арифметична прогресія. Нехай маємо арифметичну прогресію (а_n) з різницею d. Тоді для натуральних значень n > 1 виконуються рівності:

 

a_n – a_n–1 = d, a_n+1 – a_n = d.

Звідси: a_n – a_n–1 = a_n+1 – a_n;

 2a_n = a_n–1 + a_n+1;

 a_{n = .}

 

Властивість 1. Будь-який член арифметичної прогресії, починаючи з другого, є середнім арифметичним двох сусідніх з ним членів. З цією властивістю арифметичної прогресії і пов’язана її назва.

 Розглянемо скінченну арифметичну прогресію (x_n), яка має 7 членів:       3; 5; 7; 9; 11; 13; 15. Знайдемо суму крайніх членів прогресії і суми членів, рівновіддалених від крайніх:

x₁ + x₇ = 3 + 15 = 18;

 x₂ + x₆ = 5 + 13 = 18;

 x₃ + x₅ = 7 + 11 = 18;

 x₄ + x₄ = 9 + 9 = 18.

Сума будь-яких двох членів арифметичної прогресії, які рівновіддалені від її крайніх членів, дорівнює сумі крайніх членів.

Використаємо ці міркування для довільної скінченної арифметичної прогресії a₁; a₂; …; a_n з різницею d. Нехай a₁ + a_n = m. Тоді:

а₂ + а_n-1 = (a₁+d) + (a_n – d) = a₁+a_n = m;

а₃ + а_n-2 = (a₂+d) + (a_n-1 – d) = a₁+a_n = m і т.д.

 

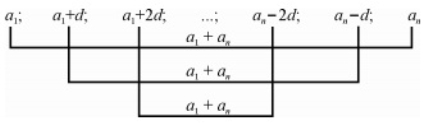
Властивість 2. Сума будь-яких двох членів скінченної арифметичної прогресії, які рівновіддалені від її крайніх членів, дорівнює сумі крайніх членів цієї прогресії. (Рис. 1)

Ввести поняття геометричної прогресії в 9-му класі можна так:

- Досі ми розглядали арифметичну прогресію, тобто числову послідовність, в якої різниця між кожним членом, крім першого, і попереднім однакова. А тепер розглянемо таку числову послідовність, в якої частка від ділення кожного члена, крім першого, на попередній однакова. Такі послідовності називають геометричними прогресіями.

Після цього можна навести приклади геометричних прогресій:

3, 6, 12, 24, 48, 96, … (b₁=3, q=2);

1, -3, 9, -27, 81, -243, …(b₁=1, q=-3);

7, 7, 7, 7, 7, 7, 7, 7, …(b₁=7, q=1),

ввести поняття знаменника прогресії і т. д. Означення можна дати аналогічне означенню арифметичної прогресії: «Геометричною прогресією називають послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне і те саме число. Це стале для даної послідовності число q називають знаменником геометричної прогресії».

Треба добитися, щоб учні вільно записували будь-яку геометричну прогресію у вигляді

b₁ , b₁·q, b₁·q², b₁·q³, …, b₁·q^n-1, … 

Ввести властивості геометричної прогресії можна аналогічно властивостям арифметичної.

Наприклад, у геометричній прогресії 1; 3; 9; 27; 81; ... квадрат кожного члена, починаючи із другого, дорівнює добутку двох сусідніх з ним членів: 3² = 1 · 9; 9² = 3 · 27; 27² = 9 · 81;... .

Покажемо, що таку властивість має будь-яка геометрична прогресія. Нехай маємо геометричну прогресію (b_n) зі знаменником q. Тоді для n > 1 виконуються рівності: , .

 Звідси: ; .

Властивість 1. Квадрат будь-якого члена геометричної прогресії, починаючи із другого, дорівнює добутку двох сусідніх з ним членів.

Якщо всі члени геометричної прогресії є додатними числами, то з рівності випливає, що . Отже, кожний член такої прогресії, починаючи із другого, є середнім геометричним двох сусідніх з ним членів. З цією властивістю геометричної прогресії і пов’язана її назва.

Розглянемо скінченну геометричну прогресію (x_n), яка містить шість членів: –1; 2; –4; 8; –16; 32. Знайдемо добуток крайніх членів цієї прогресії та добутки членів, рівновіддалених від крайніх:

x_{1 ·} x₆ = (−1) ⋅ 32 =− 32;

x₂ ⋅ x₃ = 2 ⋅ (−16) = − 32;

x₃ ⋅ x₄ = (−4) ⋅ 8 =− 32.

Бачимо, що добутки членів прогресії, рівновіддалених від її крайніх членів, однакові й дорівнюють добутку крайніх членів.

Використаємо ці міркування для довільної скінченної геометричної прогресії b₁; b₂; …; b_n. Нехай b₁· b₂ = m_.

 

Тоді:

…,

 

 

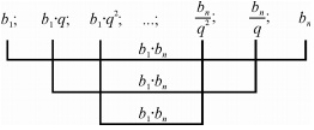
Властивість 2. Добуток будь-яких двох членів скінченної геометричної прогресії, рівновіддалених від її крайніх членів, дорівнює добутку крайніх членів. (Рис. 2)

Нескінченно спадною геометричною прогресією називають таку геометричну прогресію (b_n), у якої знаменник | q | < 1 і яка містить нескінченне число доданків.

 

 

 

 

 

 

 

 

 

 

 

1.3. Методика вивчення формул n-го члена та формул суми перших членів арифметичної та геометричної прогресії

Після введення поняття арифметичної прогресії учнів приводять до формули n-го члена та формул суми перших членів прогресії. Формулу n-го члена арифметичної та геометричної прогресії дістають в 9 класі індуктивним методом використавши неповну індукцію. Спочатку пригадують спосіб задання арифметичної прогресії, потім переконуються, що він є незручним для відшукання членів прогресії. Відомо a_n+1 = a_n + d.

Учням пропонується знайти декілька членів арифметичної прогресії у якій a₁=4, d=3. Виявляється, що наприклад a₅₀ незручно знаходити, використаємо метод неповної індукції складемо наступні рівності:

а₂ = a₁ + d,

a₃ = a₂ + d = (a₁ + d)+ d = a₁ + 2d,

a₄ = a₃ + d = (a₁ +2 d)+ d = a₁ + 3d,

… … … … … … … … … … … … … …

a_n = a₁ +(n – 1)d.

Цей метод приводить до формули n-го члена прогресії, але не є строгим доведенням.

Щоб задати геометричну прогресію досить вказати її перший член і знаменник, а наступний член геометричної прогресії можемо знайти за наступною формулою b_n+1= b_n · q.

Учням пропонується знайти кілька членів геометричної прогресії, в якій

b₁=-5, q=2. Прийдемо до висновку, що b₅₀ шукати не зручно і за означенням геометричної прогресії з’ясовуємо

b₂= b₁ · q,

b₃= b₂ · q = (b₁ · q) · q = b₁ · q²,

b₄= b₃ · q = (b₁ · q²) · q = b₁ · q³,

… … … … … … … … … … … …

b_n = b₁ · q^n-1.

Перед введенням суми перших n членів арифметичної прогресії у загальному вигляді розглядають приклад знаходження суми натуральних чисел від 1 до 100.

Приклад.

Знайти суму натуральних чисел від 1 до 100.

 S = 1 + 2 + 3 + … + 98 + 99 + 100

+

 S = 100 + 99 + 98 + … + 3 + 2 + 1

 2S = 101 + 101 + 101 + … +101 + 101 + 101

 2S = 101 · 100

 S = 101 · 50 = 5050.

Цей же прийом використовують для виведення формули суми n-перших членів арифметичної прогресії. З попереднього прикладу учні розуміють, що в розглянутому прикладі

a₁ = 1; n = 100; d = 1.

В загальному виді ми будемо шукати суми S_n

 S_n = a₁ + a₂ + a₃ + … + a_n-2 + a_n-1 + a_n

+

 S_n = a_n + a_n-1 + a_n-2 + … + a₃ + a₂ + a₁

Додавши одержані рівності отримаємо

 2S_n = ( a₁ + a_n ) + ( a₂ + a_n-1 ) + ( a₃ + a_n-2 ) + … + ( a_n-1 + a₂ )+ ( a_n + a₁ ).

 За властивістю арифметичної прогресії сума двох членів скінченної арифметичної прогресії, рівновіддалених від початку і кінця, дорівнює сумі першого і останього членів, отримаємо формулу

S_n = (1)

Другу форму для обчислення суми дістають підставивши у формулу (1) формулу a_n = a₁ +(n – 1)d отримаємо

S_n = .

Аналогічно можна вивести формулу суми n перших членів геометричної прогресії в загальному вигляді:

S_n = b₁ + b₁q + b₁q² + … + b₁q^{n -1};

S_n = b₁ + q ( b₁ + b₁q + … + b₁q^{n -2});

S_n = b₁ + q (S_n - b₁q^{n -1});

S_n = b₁ + qS_n - b₁qⁿ;

qS_n - S_n = b₁qⁿ - b₁;

S_n ( q – 1) = b₁ (qⁿ - 1);

S_n = , q ≠ 1.

Урахувавши, що b₁ = , одержимо S_n = .

Ознайомлення учнів з формулою суми нескінченної геометричної прогресії, у якій |q| < 1 краще за все почати з розв’язання задачі.

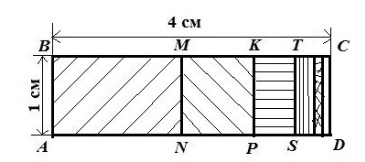Нехай маємо прямокутник ABCD зі сторонами 1 см і 4 см (Рис. 3). Його площа дорівнює 1 · 4 = 4 (см²).

Знайдемо площу цього прямокутника по-іншому.

Відрізком MN, що з’єднує середини протилежних сторін BC і AD прямокутника, поділимо його навпіл. Площі утворених прямокутників ABMN і NMCD дорівнюють по 2 см². Утворений праворуч прямокутник знову поділимо навпіл, з’єднавши середини K і Р протилежних сторін. Площі утворених прямокутників NMKP і PKCD дорівнюють по 1 см². Аналогічно утворений прямокутник PKCD знову поділимо навпіл відрізком TS на два прямокутники з площами по см² і т.д.

Знайдемо суму площ прямокутників ABMN, NMKP, PKTS і т. д. Числове значення суми площ цих прямокутників дорівнюватиме сумі чисел

2; 1; ; ... . Послідовність 2; 1; ; ... є нескінченною геометричною прогресією, перший член якої дорівнює 2, а знаменник - .

Знайдемо суму перших n членів цієї прогресії:

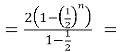
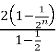
S_n 4 · .

Якщо число n доданків суми S_n необмежено збільшується, то значення

дробу наближається до нуля, а різниця наближається до числа 4, кажуть: прямує до числа 4. Число 4 називають сумою нескінченної геометричної прогресії 2; 1; ; ... і записують 2 + 1 + + ... = 4. Отже, сума площ прямокутників ABMN, NМKP, PKTS і т. д. дорівнює 4 см², тобто дорівнює площі прямокутника ABCD.

Узагальнимо розглянутий приклад.

Нехай b₁; b₂; b₃; … – довільна нескінченна геометрична прогресія, у

якій |q| < 1. Сума перших n членів цієї прогресії обчислюється за формулою S_n = , q ≠ 1. Перетворимо вираз у правій частині останньої рівності: S_n = . Оскільки |q| < 1, то при необмеженому збільшенні n множник qⁿ прямує до нуля, а, отже, до нуля прямує і добуток .

Тоді сума S_n прямує до числа . Число називають сумою нескінченної геометричної прогресії зі знаменником |q| < 1 і записують:

 b₁ + b₂ + b₃ + … = .

Позначимо цю суму через S. Тоді S = .

Одержану формулу називають формулою суми нескінченної геометричної прогресії, у якій |q| < 1.

 

 

 

 

1.4.  Прогресії та їх практичне застосування

Внутрішня гармонія, строга краса роблять теорію арифметичної і геометричної прогресії відображенням фундаментальних властивостей об’єктивного світу, що існує незалежно від нас. Тривале життя прогресій зумовлене не тільки їх цікавими властивостями, а й широкими можливостями їх застосування в інших наукових галузях.

Прогресії у фізиці. Прогресії виражають закони деяких фізичних явищ. Наприклад, за законом геометричної прогресії здійснюється поділ нейронів при середній ланцюговій реакції. У фізиці є таке поняття як «рівноприскорений рух». Якщо кажуть, що тіло рухається рівноприскорено, то це означає, що відстань, яку воно проходить за кожну наступну одиницю часу збільшується на одну й ту саму величину. Рух також може бути і рівноповільним. Таким чином, відрізки шляху, які проходить тіло за 1-шу, 2-гу, 3-тю, 4-ту одиницю часу, утворюють арифметичну прогресію.

Прогресії в біології. В біології також є явища, які можна охарактеризувати за допомогою прогресій. Одним з таких явищ є розмноження живих організмів. Знаючи такі характеристики організму, як періодичність відтворення та кількість потомства, можна за допомогою прогресій спрогнозувати кількість популяцій за певний проміжок часу.

Прогресії в проектуванні. Аналогічно в соціальних науках теорія прогресій дає змогу обчислити приріст населення. В проектуванні стає питання, на яке може дати відповідь математика.

Прогресії а економіці. Існує думка, що разом з винаходом колеса, створення банків стало одним з найважливіших винаходів людства. Перший банк був заснований 1171 року, з того часу банківська система розширюється і вдосконалюється. Якщо розмістити до ощадбанку грошовий вклад, то банк виплачує вкладнику деяку суму грошей за те, що користується його капіталом для надання позик. За кожний рік початковий внесок збільшується в одне й те саме число разів. Тобто приріст вкладу зростає за законом геометричної прогресії.

Розділ 2. Задачі пов’язані з прогресіями та методика навчання їх розв’язання

2.1. Методика навчання учнів розв’язання задач пов’язаних арифметичною прогресією

2.1.1 Задачі на знаходження членів арифметичної прогресії, використовуючи формулу n-го члена і властивості арифметичної прогресії.

При розв'язуванні вправ крім закріплення термінології та формул, що виражають властивості, проводиться відпрацювання таких ключових моментів: як перевірити, чи є задана послідовність арифметичною прогресією (за означенням, або за характеристичною властивістю, або за теоремою, залежно від умови); як знайти різницю арифметичної прогресії (від будь-якого члена, починаючи з другого, відняти попередній до нього член); як знайти член, наступний за даним членом арифметичної прогресії (знайти різницю арифметичної прогресії й додати її до даного члену).

Наприклад, можна розпочати роботу з нескладних вправ:

Вправа 1.

Дано скінченну послідовність: (х_n): 3; 0; -3; -6; -9; -12. Укажіть:

1) перший, третій, шостий члени цієї послідовності;

2) чи є ця послідовність зростаючою, спадною;

3) формулу її n-го члена.

Розв’язання.

1) перший член послвдовності = 3 , третій = -3, шостий = -12;

2) послідовність є спадною, тому що кожний наступний член менший за попередній.

3) формулу її n-го члена - (х_n) = 3 - 3п , де п = 0, 1, 2, ….

Вправа 2.

Чи є послідовність чисел 3; 0; –3; –6; –9 арифметичною прогресією?

Розв’язання.

 Позначимо члени заданої послідовності: a₁ = 3; a₂ = 0; a₃ = –3; a₄ = –6; a₅ = –9. Знайдемо різниці наступного та попереднього членів послідовності:

a₂ – a₁ = 0 – 3 = –3; a₃ – a₂ = –3 – 0 = –3;

a₄ – a₃ = –6 – (–3) = –3; a₅ – a₄ = –9 – (–6) = –3.

Оскільки одержані різниці дорівнюють одному й тому ж числу –3, то ця послідовність є арифметичною прогресією.

Вправа 3.

Перший член арифметичної прогресії дорівнює -3, а різниця 2. Чому дорівнює другий член цієї прогресії?

Розв’язання.

Щоб задати арифметичну прогресію, досить вказати її перший член і різницю. Тоді кожний наступний член можна обчислити через попередній за рекурентною формулою a_n+1 = a_n + d.

Використавши рекурентну формулу а₂ = а₁ + d отримаємо:

а₂ = -3 + 2;

а₂ = -1.

Відповідь: -1.

При розв’язанні вправ учні повинні знати відповіді на запитання:

1. Що називається арифметичною прогресією?

2. Як знайти різницю арифметичної прогресії?

3. Сформулюйте властивості арифметичної прогресії.

Для усвідомлення учнями необхідності вивчення формули п-го члена арифметичної прогресії та подальшого її застосування можна запропонувати їм виконати таку вправу: знаючи перший член та різницю арифметичної прогресії, знайти її деякий член (номер якого є достатньо великим).

Усвідомивши нераціональність розв'язування задачі відомим учням способом (через застосування рекурентної формули), вони приходять до запитання: чи не існує способу знаходження будь-якого члена арифметичної прогресії без необхідності знаходити попередні кілька її членів? Пошук відповіді на це запитання – формула n-го члена прогресії.

Приклад 1.

В арифметичній прогресії а₁ = 4, d = 3. Знайдіть а₂₀.

Розв’язання.

а₂₀ = а₁ + 19d = 4+ 19·3 = 61.

Відповідь 61.

Запропонувати учням розв’язати інші задачі для закріплення означення та формули, уже вивчених, а також для вироблення оперативних умінь із застосування формул при розв'язуванні задач в різних ситуаціях.

Приклад 2.

Знайти дев’ятий член арифметичної прогресії (a_n): 5; 4,2; 3,4; ... .

Розв’язання.

Маємо: a₁ = 5.

Знайдемо різницю прогресії: d = 4,2 – 5 = –0,8.

Тоді a₉ = a₁ + 8d = 5 + 8 · (–0,8) = –1,4.

Відповідь. –1,4.

 

 

 

2.1.2 Задачі на відшукання суми перших послідовних n членів арифметичної прогресії

Вивчення матеріалу починається з виведення формули суми перших n членів арифметичної прогресії через перший і n-й члени та другої формули для обчислення суми перших n членів арифметичної прогресії через перший її член і різницю. Після вивчення обох формул слід наголосити на тому, що вибір формули для розв'язування конкретної задачі зумовлений даними задачі.

Приклад 1.

Знайти суму перших дев’яти членів арифметичної прогресії (a_n): 3; 7;11;...

Розв’язання.

1-й спосіб. Маємо: a₁ = 3, d = a₂ – a₁ = 7 – 3 = 4.

Знайдемо а₉:      a₉ = 3  + 8 · 4 = 35.

За першою формулою суми перших n членів арифметичної прогресії через перший і n-й члени знаходимо:

S₉ = = 171.

2-й спосіб. Знаючи, що a₁ = 3, d = 4, за другою формулою для обчислення суми перших n членів арифметичної прогресії через перший її член і різницю знаходимо:

S₉ = = 171.

Відповідь. 171.

Приклад 2.

Знайти суму непарних натуральних чисел, які не перевищують 71.

Розв’язання.

Непарні натуральні числа утворюють арифметичну прогресію 1; 3; 5;..., у якій a₁ = 1, d = 2, a_n = 1 + (n – 1) · 2 = 2n – 1.

Знайдемо, який порядковий номер має член 71 цієї прогресії:

71 = 2n – 1; n = 36.

Отже, потрібно шукати суму перших тридцяти шести членів прогресії. Знаходимо:

S = · 36 = 1296.

Відповідь. 1296.

Приклад 3.

Знайти перший член арифметичної прогресії (а_n), якщо сума другого і дванадцятого її членів дорівнює 20,4, а сума перших одинадцяти – 121.

Розв’язання.

 За умовою маємо: a₂ + a₁₂ = 20,4; S₁₁ = 121. Використавши формули n-го члена та суми перших n членів арифметичної прогресії, одержимо систему рівнянь

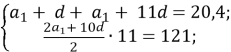Звідси :

Відповідь. 15.

При розв'язуванні вправ закріплюється знання формул та усвідомлення відмінності ситуацій, у яких виправдане застосування однієї з вивчених формул, а також формуються вміння працювати із вивченими формулами в різних напрямках: як для відшукання значення суми арифметичної прогресії, так і для відшукання за даною сумою інших даних (першого члена арифметичної прогресії, або її різниці, або кількості перших членів, для яких відома їхня сума).

 

2.1.3 Прикладні задачі пов’язані з арифметичною прогресію

В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, формені елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії. За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

Задача.

Кількість еритроцитів ( з розрахунку на 1 мм³) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест 

(4800 м) .

Розв’язання.

Проаналізуємо цю задачу. Склавши математичну модель цієї задачі ми отримаємо, що кількість еритроцитів в крові людини збільшується за арифметичною прогресією.

З умови нам дано a₁=5, d = 1, h = 4800, h₁ = 600. Потрібно знайти a_n.

Спочатку знайдемо значення n.

n = = = 8

Підставимо відомі значення у формулу              a_n = a₁ + (n – 1)d,

 отримаємо

a₈ = a₁ + 1(n – 1) = 5 + 7 = 12 (млн).

Відповідь: 12 млн.

Задача пов’язана з фізикою.

Гальмуючи, автомобіль за першу секунду проїхав 15 м, а за кожну наступну – на 3 м менше, ніж за попередню. Знайдіть гальмівний шлях автомобіля.

Розв’язання.

Для того, щоб правильно розв’язати задачу потрібно уважно прочитати умову. Ми побачимо, гальмівний шлях утворює арифметичну прогресію.

З умови ми бачимо, що нам дано a₁ =15, d = -3, a_n = 0.

Нам потрібно знайти S_n – гальмівний шлях.

Спочатку потрібно знайти п. Використаємо формулу a_n = a₁ + d(n – 1), отримаємо

15 – 3(n -1) = 0,

n = 6.

Тепер можемо порахувати S_n – гальмівний шлях, використавши першу формулу відшукання суми перших послідовних n членів арифметичної прогресії.

S₆ = · 6 = 15 · 3 = 45 (м) – гальмівний шлях автомобіля.

Відповідь: 45 м.

 

 

 

 

 

 

 

2.2 Методика навчання учнів геометричної прогресії

2.2.1 Задачі на знаходження членів геометричної прогресії, використовуючи формулу n-го члена і властивості геометричної прогресії

При розв'язуванні вправ, крім закріплення термінології та формул, що виражають властивості геометричної прогресії, проводиться відпрацювання схем дій у таких стандартних ситуаціях: перевірити, чи є задана послідовність геометричною прогресією (за означенням, або за характеристичною властивістю, або за теоремою, залежно від умови); знайти знаменник геометричної прогресії, якщо відомі два сусідні її члени; знайти член, наступний за даним членом геометричної прогресії. Так само, як при вивченні питання про формулу n-го члена арифметичної прогресії, роботу на цьому етапі організуємо як колективний пошук розв'язання задачі: як найраціональнішим способом знайти значення n-го члена геометричної прогресії, знаючи її перший член і знаменник. Розпочати вивчення геометричної прогресії можна з таких завдань.

Приклад 1.

Знайти знаменник і третій член геометричної прогресії (b_n): 1; 1,5; … .

Розв’язання:

У цій прогресії b₁ = 1, b₂ = 1,5. Тому: q = = = 1,5;

b₃ = b₂ · q = 1,5 ·1,5 = 2,25.

Відповідь. 1,5; 2,25.

Приклад 2.

Довести, що послідовність 8; –4; 2; –1; є геометричною прогресією.

Доведення:

Позначимо члени послідовності: b₁ = 8; b₂ = –4; b₃ = 2; b₄ = –1; b₅= . Знайдемо частки від ділення наступного члена послідовності на попередній:

;

;

;

.

Оскільки одержані частки дорівнюють одному й тому ж числу , то задана послідовність є геометричною прогресією зі знаменником .

Приклад 3.

Знайти знаменник геометричної прогресії (b_n), у якій b₇ = –12, b₉ = –108

Розв’язання:

Використавши формулу n-го члена геометричної прогресії, одержимо:

b₉ = b₁q⁸ = –108, b₇ = b₁q⁶ = –12. Звідси:

; q ² = 9; q = –3 або q = 3.

Відповідь. –3 або 3.

 

 

 

2.2.2 Задачі на відшукання суми n перших членів геометричної прогресії

Запропонований набір вправ спрямований на закріплення формул для обчислення суми перших n членів геометричної прогресії, на вироблення оперативних умінь щодо їх застосування в стандартних ситуаціях як в прямому, так і в зворотному напрямі.

Приклад 1.

Знайти суму восьми перших членів геометричної прогресії (b_n):

3; –6; 12; ... .

Розв’язання:

Маємо: b₁ = 3; q = = -2. Тоді за формулою S_n = знаходимо: S₈ = = = –255.

Відповідь. –255.

Приклад 2.

Знайти перший член геометричної прогресії (b_n), якщо четвертий її член утричі більший від третього, а сума перших п’яти членів дорівнює -12,1.

Розв’язання:

Оскільки b₄ = 3b₃, то q = 3. За умовою S₅ = –12,1, тому:

–12,1 = ; –12,1 = 121 · b₁; b₁ = -0,1.

Відповідь. -0,1.

 

 

 

 

2.2.3 Задачі на відшукання суми нескінченно спадної геометричної прогресії

При ознайомленні учнів з формулою знаходження суми нескінченної геометричної прогресії краще спочатку розглянути кілька нескінченних геометричних прогресій зі знаменником, модуль якого менший за одиницю, і звернути увагу на те, що зі збільшенням номера члена прогресії його знаменник стає все ближчим до нуля. Далі запропонувати розглянути суму нескінченної геометричної прогресії, якщо |q| < 1. Вивчення матеріалу будується на наочно-інтуїтивних уявленнях учнів про границю послідовності. Важливо підкреслити, що формула виведена для суми всіх членів нескінченної геометричної прогресії зі знаменником | q | < 1, а тому відрізняється від формули суми перших n членів геометричної прогресії.

Приклад 1.

Знайти суму нескінченної геометричної прогресії (b_n): 6; –2; … .

Розв’язання:

За умовою маємо: b₁ = 6; b₂ = –2. Тоді маємо геометричну прогресію, у якій |q| < 1. За формулою S = знаходимо:

S = 4,5.

Відповідь. 4,5.

Приклад 2.

Запишіть число 0,(7) у вигляді звичайного дробу.

Розв’язання:

Запис 0,(7) означає нескінченний періодичний дріб 0,7777....

Його можна подати як нескінченну суму  + + + … .

Доданки цієї суми є членами нескінченної геометричної прогресії, у якої b₁ = , q = : = , |q| < 1. Тоді ця сума дорівнює:

S = . Тому 0,(7) = .

Відповідь. .

Приклад 3.

Знайдіть перший член нескінченної геометричної прогресії, у якій q = , S = 50.

Розв’язання:

У формулу суми нескінченної геометричної прогресії підставимо відомі значення та виразимо перший член прогресії.

50 = ; 50 = ; 50 = ; = 20;

20.

 

 

 

 

 

 

 

 

Висновки

 

Дана робота присвячена методиці вивчення арифметичної та геометричної прогресії в шкільному курсі алгебри.

Вивчення навчально–методичної літератури дозволило нам виконати такі завдання:

1) систематизувати теоретичні відомості про арифметичні та геометричні прогресії, їх властивості;

2) дослідити методику навчання учнів розв’язування задач пов’язаних з арифметичною і геометричною прогресією на різних рівнях навчання;

3) підібрати систему задач пов’язаних з прогресіями.

 Створена технологія навчання прогресій в курсі алгебри містить у собі методи, що стимулюють формуванню інтелектуального потенціалу учнів, розвитку їхніх пізнавальних інтересів і творчої активності. Запропонована методика є ефективною тому, що в ній вдало використано пояснювально – ілюстративний та конкретно-індуктивний методи для глибокого і міцного засвоєння учнями знань, а також підібрана система задач, пов’язаних з арифметичною і геометричною прогресією, місить задачі початкового, середнього, достатнього і восокого рівня складності.

 

Список використаної літератури

1. Алгебра для загальноосвітніх навчальних закладів з поглибленим вивченням математики: підруч. для 9 кл. Загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х. : Гімназія, 2017. – 416с.

2. Бевз Г.П. Алгебра: підруч. для 9 кл. загальноосвіт. навч. закл./ Г.П. Бевз, В.Г. Бевз. –К.: Зодіак-ЕКО, 2009. – 281с.

3. Бевз Г.П. Методика викладання математики 3-тє вид., доп. та перероб. – К.: Вища школа, 1989. – 367 с.

4. Гошина, Н. А. Арифметична прогресія. Сума перших n членів арифметичної прогресії : алгебра, 9 клас / Н. А. Гошина // Математика в шк. України. – 2013. – №10. – С. 21-23.

5. Давиденко, С. Сума n перших членів геометричної прогресії: (Урок алгебри у 9-му класі) / С. Давиденко // Математика. – 2005. – №2(січень). – С. 9 - 11.

 6. Дудар, Г. Арифметична і геометрична прогресії : алгебра, 9 клас / Г. Дудар // Математика. – 2011. – №18 (травень). – С. 13-14.

7. Кравчук В., Підручна М., Янченко Г. Алгебра. Підручник для 9 класу. Тернопіль: Підручники і посібники, 2004.-248с. – С. 170-200.

8. Левус, О. І. Числові послідовності. арифметична прогресія. 9 клас : [система уроків із теми] / О. І. Левус // Математика в шк. України. – 2017. – № 7-8. – С. 40-46.

9. Лисенко, Н. Г. Розв'язування вправ і задач на прогресії. 9 клас / Н. Г. Лисенко // Математика в шк. України (наук.-метод. журн.). – 2017. – № 12. – С. 15-22.

10. Методика викладання математики в середній школі: [Навч. посібник для пед. ін.-тів. Пер. з рос./ О.Я. Блох, Є.С. Канін та ін.]; Упоряд. Р.С. Черкасов, А.А. Столяр.- Х.: Вид.-во ”Основа” при Харк. ун-ті. -1992.-304с.

11. Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра : Підручник для 9 класу. – Х.: Гімназія, 2009. – С. 35-39.

12.Мерзляк А.Г., Полонський В.Б., Якір М.С. Збірник задач і контрольних робіт з алгебри для 9 класу. – Х.: Гімназія. 2009. – 128 с. – С. 69-74.

13. Моргун О.О., Фурман М.С. Алгебра 9.-Х.: Вид. група ”Основа”, 2006.-224с.

14. Навчальні програми для загальноосвітніх навчальних закладів: Математика; Інформатика. 5-9 класи. - К.: Видавничий дім «Освіта», 2013.-96с.

15. Никитчук, Л. П. Арифметична прогресія / Л. П. Никитчук // Все для вчителя. – 2011. – №1. – С. 10.

16. Ніколаєнко, В. М. Прогресії та їх практичне застосування / В. М. Ніколаєнко // Все для вчителя. – 2011. – №1. – С. 70-71.

17. Попадюк, І. Розв'язування задач на арифметичну та геометричну прогресії : урок алгебри в 9-му класі / І. Попадюк // Математика. – 2015. – №3(лют.). – С. 43-47.

Размещено на Allbest.ru