Метоодичний посібник для вчителів та учнів "Многокутники. Площі многокутників"
Н. Г. Ювковецька
МНОГОКУТНИКИ.
ПЛОЩІ МНОГОКУТНИКІВ
Методичний посібник
для учителів та учнів
У методичному посібнику розроблено рекомендації щодо вивчення теми «Многокутники. Площі многокутників». Основна мета її вивчення - забезпечити засвоєння учнями істотних властивостей і ознак окремих видів чотирикутників, правильних багатокутників і навчити застосовувати здобуті знання до розв'язування різних видів задач.
Посібник містить нестандартні ситуації, роботу в групах та малих групах, цікаві та історичні задачі, задачі підвищеного рівня складності, кросворди, математичні диктанти та тестові завдання, для контролю навчальних досягнень призначена добірка рівневих самостійних робіт та тематична контрольна робота. Може використовуватись як для індивідуальної, так і для колективних форм роботи у загальноосвітніх школах.
Автор посібника:
Наталія Григорівна Ювковецька
ЗМІСТ
Вступ…………………………………………………………………………………………….4
Зміст програми з геометрії (8 клас)…………………………………………………………..5
Календарне планування з геометрії по темі «Многокутники. Площі многокутників»…..6
Тема 1. Многокутник та його елементи. Сума кутів опуклого многокутника……………9
Тема 2: Поняття площі многокутника. Площа прямокутника……………………………16
Тема 3. Розв’язування задач. Самостійна робота………………………………………...22
Тема 4. Площа паралелограма………………………………………………………………25
Тема 5. Площа трикутника………………………………………………………………….31
Тема 6. Площа трапеції……………………………………………………………………...39
Тема 7. Розв’язування задач. Самостійна робота………………………………………...45
Тема 8. Систематизація знань. Підготовка до контрольної роботи………………………49
Тема 9. Тематична контрольна робота……………………………………………………..54
Многокутники навколо нас………………………………………………………………….57
Висновок…………………………………………………………………………………...…60
Список літератури……………………………………………………………………………61
ВСТУП
Розумова праця на уроках математики – пробний камінь мислення.
В. О. Сухомлинський
Значне місце в системі формування інтелектуальної та творчої особистості школяра приділяється вивченню геометрії як дисципліни, яка володіє величезним гуманітарним та світоглядним потенціалом. Вона розвиває логічне мислення і просторову уяву школярів, має великі можливості для показу сили наукових методів у пізнанні навколишнього світу, з'ясування процесу формування понять і шляхів виникнення, представляє важливу складову математики і є одним з основних компонентів загальнолюдської культури.
Процес навчання геометрії учнів передбачає досягнення двох самостійних, але взаємозв’язаних завдань: оволодіння учнями змістом конкретного розділу та цілеспрямоване формування у них прийомів розумової діяльності, помітне місце у якій займає дослідження розвитку просторового мислення. Це здійснюється у процесі розв’язування різних геометричних задач, через використання унаочнення а також прикладів із оточуючого середовища.
Для того щоб у дітей розвивалось просторове мислення, потрібно щоб вони вміли аналізувати фігуру, виділяти її елементи, встановлювати взаємне розміщення, та з’ясовувати властивості відношень між елементами фігур і т. д.
Серед задач які є в геометрії існують задачі на дослідження. Саме в цих задачах розглядають взаємне розміщення величин, умови існування фігур, властивості відношень між елементами фігур, що є основою розвитку просторового мислення школярів основної школи Для досягнення високого рівня геометричної підготовки учнів необхідно забезпечити можливість придбання ними глибоких фундаментальних знань, розвитку просторової уяви, прагнення до самостійного вивчення нового матеріалу. Вирішенню цієї проблеми сприяє розв’язування геометричних задач на дослідження що є ефективним засобом управління пізнавальною діяльністю і формуванням просторового мислення учнів.
У посібнику пропоную розглянути тему «Многокутники. Площі многокутників» - це одна з найважливіших тем геометрії та найбільших тем курсу планіметрії 8 класу. Основна мета її вивчення - забезпечити засвоєння учнями істотних властивостей і ознак окремих видів чотирикутників, правильних багатокутників і навчити застосовувати здобуті знання до розв'язування різних видів задач.
Під час вивчення цієї теми створюються сприятливі умови для розвитку логічного мислення учнів, для формування вміння проводити класифікацію понять, вказуючи структурні зв’язки між ними, використання вивченого навчального матеріалу для розв'язування різних задач, зокрема практичних, оволодіння методами розв'язування задач і доведення теорем. Аналізуючи наочний матеріал і виконуючи безпосередні вимірювання, учні мають можливість значну кількість властивостей многокутників встановити самостійно. Оскільки більшість терем теми нескладні для доведення і безпосередньо спираються на вивчені ознаки рівності трикутників і паралельності прямих, то є можливість організувати самостійний пошук доведень. Варто зважати на те, що деякі види чотирикутників, формули для обчислення їх периметрів та площ учні вивчають на наочно-інтуїтивному рівні ще у 1 – 6-х класах. На цьому етапі відбувається пропедевтика вивчення чотирикутників і вони переважно є дидактичним засобом засвоєння арифметичного матеріалу та метричної системи мір. У 7 – 9-х класах многокутники вже є безпосередніми об’єктами вивчення.
Готуючись до уроків, я намагаюсь подати матеріал так, щоб він пройшов через емоційну сферу учня, яку збуджують нестандартні уроки, проблемні ситуації, цікаві та ігрові моменти, історичні факти, поезія, самостійні дослідження. Такий підхід робить процес навчання захоплюючим, цікавим і ефективним.
Зміст програми з геометрії (8 клас)
Тема. Многокутники. Площі многокутників (12 год)
|
Очікувані результати навчально-пізнавальної діяльності учнів |
Зміст навчального матеріалу |
|
Учень/учениця: наводить приклади геометричних фігур, указаних у змісті; пояснює, що таке: многокутник та його елементи; площа многокутника; многокутник, вписаний у коло та описаний навколо кола; формулює:
записує та пояснює формули площі геометричних фігур, указаних у змісті; зображає та знаходить на малюнках: многокутник і його елементи; многокутник, вписаний у коло; многокутник, описаний навколо кола; співвідносить з об’єктами навколишньої дійсності вказані у змісті фігури; обчислює площі вказаних у змісті фігур; застосовує вивчені означення, властивості та формули до розв’язання задач, зокрема знаходження площ реальних об’єктів; розв’язує задачі на: розбиття многокутника на рівновеликі; дослідження рівноскладеності многокутників тощо |
Многокутник та його елементи.
Многокутник, вписаний у коло, і многокутник, описаний навколо кола.
Поняття площі многокутника.
Площі прямокутника, паралелограма, ромба, трикутника, трапеції |
|
Розв’язує задачі практичного змісту на: визначення відстані до недоступної точки; висоти предмета; знаходження кутів (кута підйому дороги, відкосу, кута, під яким видно деякий предмет) тощо |
|
Календарне планування з геометрії по темі «Многокутники. Площі многокутників»
|
№п/п |
Кількість годин |
Тема уроку |
Мета уроку |
|
1 |
2 |
Многокутник та його елементи. Сума кутів опуклого многокутника. Многокутник, вписаний у коло, і многокутник, описаний навколо кола |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
2 |
2 |
Поняття площі многокутника. Площа прямокутника |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
3 |
1 |
Розв’язування задач. Самостійна робота |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
4 |
2 |
Площа паралелограма |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
5 |
3 |
Площа трикутника |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
6 |
3 |
Площа трапеції |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
7 |
1 |
Розв’язування задач. Самостійна робота |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
8 |
1 |
Систематизація знань. Підготовка до контрольної роботи |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
|
9 |
1 |
Тематична контрольна робота |
Навчальна складова:
Розвивальна складова:
Виховна складова:
|
Многокутники. Площі многокутників
Тема 1: Многокутник та його елементи. Сума кутів опуклого многокутника. Многокутник, вписаний у коло, і многокутник, описаний навколо кола.
Мета:
Навчальна складова:
- Сформувати в учнів поняття замкненої ламаної, многокутника, елементів многокутника, рівних фігур, ознайомити з видами многокутників;
- навчити розпізнавати многокутники, наводити приклади рівних фігур, використовувати набуті знання до розв'язування практичних задач.
Розвивальна складова:
- розвивати вміння виділяти головне, аналізувати та розвивати просторову уяву.
Виховна складова:
- Виховувати комунікативність, математичне мовлення, графічну культуру учнів.
Зміст теоретичного матеріалу
- Означення замкненої ламаної.
- Означення многокутника та його елементів.
- Означення многокутника вписаного у коло та многокутника, описаного навколо кола.
- Теорема про суму кутів опуклого n-кутника.
Методичні поради
Під час викладання теоретичного матеріалу пропоную використати слайди презентації «Многокутники»
Ламана
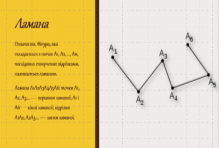 Означення. Фігура, яка складається з точок А1, А2, ..., Аn, послідовно сполучених відрізками, називається ламаною.
Означення. Фігура, яка складається з точок А1, А2, ..., Аn, послідовно сполучених відрізками, називається ламаною.
Ламана А1А2А3А4А5А6: точки А1, А2, А3.... — вершини ламаної; А1 і А6 — кінні ламаної; відрізки А1А2, А2А3.... — ланки ламаної.

Фігура, утворена кінцевим набором відрізків, розташованих так, що кінець першого є початком другого, кінець другого - початком третього і т.д., називається ламаною лінією або простою ламаною (рис. 1). Відрізки називаються сторонами ламаної, а їх кінці - вершинами ламаною.
Ламана позначається послідовним зазначенням її вершин. Наприклад, ламана АВС DE, ламана A 1 A 2 ... A n.
Ламана називається простою, якщо вона не має точок самоперетинання (рис. 2).
Ламана називається замкнутою, якщо початок першого відрізка ламаної збігається з кінцем останнього. Замкнуту ламану, у якої точками самоперетинання є тільки початкова та кінцева точки, також називають простий (рис.3).
Довжиною ламаної називається сума довжин її сторін.
 Многокутник (багатокутник, полігон) — геометрична фігура, замкнена ламана (сама, або разом із точками, що лежать усередині). Вершини цієї ламаної називають вершинами многокутника, а відрізки ламаної — сторонами многокутника.
Многокутник (багатокутник, полігон) — геометрична фігура, замкнена ламана (сама, або разом із точками, що лежать усередині). Вершини цієї ламаної називають вершинами многокутника, а відрізки ламаної — сторонами многокутника.
Дві вершини, що сполучаються відрізком ламаної, називаються суміжними вершинами. Дві сторони, що мають спільну вершину називаються суміжними. Якщо дві несуміжні сторони не мають спільних точок (тобто ламана, що обмежує многокутник, не перетинається), многокутник називається простим.
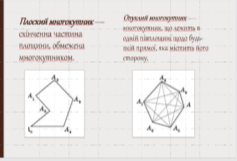 Плоский та опуклий многокутники
Плоский та опуклий многокутники
Плоский многокутник — скінченна частина площини, обмежена многокутником
Опуклий многокутник — многокутник, що лежить в одній півплощині щодо будь-якій прямої, яка містить його сторону.
 Кутом многокутника при даній вершині називають кут, утворений його сторонами, які сходяться в цій вершині.
Кутом многокутника при даній вершині називають кут, утворений його сторонами, які сходяться в цій вершині.
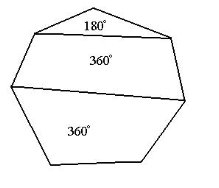
Сума кутів опуклого многокутника дорівнює.
Зовнішнім кутом многокутника при даній вершині називають кут, суміжний із внутрішнім кутом многокутника при цій вершині.
Сума зовнішніх кутів опуклого n-кутника, взятих по одному при кожній вершині, дорівнює 360°.

Многокутник називається вписаним у коло, якщо всі його вершини належать колу. Це коло називається описаним навколо многокутника.
Центром такого кола є точка перетину серединних перпендикулярів, проведених до всіх сторін многокутника.
Правильним є обернене твердження: якщо серединні перпендикуляри, проведені до всіх сторін многокутника, перетинаються в одній точці, то навколо даного многокутника можна описати коло.
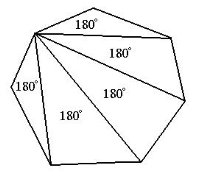
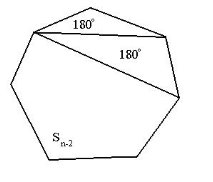
Теорема (про суму кутів опуклого n-кутника). Сума кутів опуклого n-кутника дорівнює 180º(n-2).
Доведення
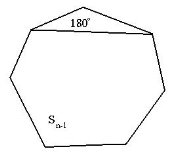
І спосіб
1-й крок. п-кутник розбивається діагоналлю, що виходить з вершини, на трикутник і п-1-кутник.
Тоді сума кутів п-кутника Sn=180° + Sn-1, де Sn-1– сума кутів п-кутника.
2-й крок. Знаходимо Sn-1, розбиваючи п-1-кутник другою діагоналлю, що виходить із тієї ж вершини многокутника, на трикутник і п-2-кутник.
Тоді
Sn-1= 180°+ Sn-2,
Sn = 180°+ (180° + Sn-2),
І так розбиваємо п-кутник доти, доки останній із многокутників п-3-ю діагоналлю не буде розбитий на п-2 трикутники:
Sn= 180° (n-3) + 180°;
Sn= 180° (n-2).
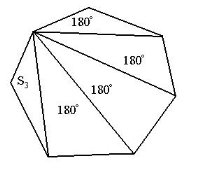
ІІ спосіб
Якщо п – кількість сторін многокутника, то п-2 – кількість утворених трикутників діагоналями, що виходять з однієї вершини.
Сума кутів даного многокутника дорівнює сумі усіх цих трикутників:
Sn= 180° (n-2).
ІІІ спосіб
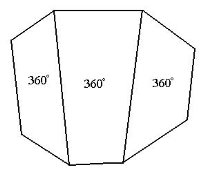
1.Нехай в опуклому п-кутнику парна кількість сторін. Розіб’ємо його діагоналями на чотирикутники.
- кількість утворених чотирикутників. Сума кутів даного п-кутника дорівнює сумі цих чотирикутників:
Sn = 360°,
Sn = 180° (n-2).
 2. Нехай в опуклому п-кутнику непарна кількість сторін. Розіб’ємо його діагоналями на чотирикутники та один трикутник.
2. Нехай в опуклому п-кутнику непарна кількість сторін. Розіб’ємо його діагоналями на чотирикутники та один трикутник.
Сума кутів даного п-кутника дорівнює сумі кутів усіх чотирикутників та кутів трикутника:
Sn = 360°· + 180°,
Sn = 180° (n-2).
ІV спосіб
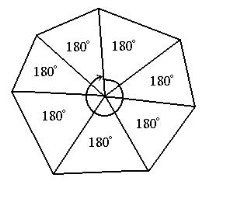
Виберемо довільну внутрішню точку опуклого п-кутника і з’єднаємо її з усіма вершинами.
Отримаємо п трикутників зі спільною вершиною у точці О. Сума всіх кутів при вершині - 360°. Сума кутів усіх трикутників 180°×п. Тоді 180°п = Sn + 360°, де Sn – сума кутів п-кутника. Отже,
Sn = 180°п-360°,
Sn = 180° (n-2).
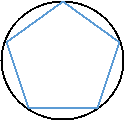 Многокутник називають вписаним у коло, якщо всі його вершини лежать на колі. Коло при цьому називають описаним навколо многокутника.
Многокутник називають вписаним у коло, якщо всі його вершини лежать на колі. Коло при цьому називають описаним навколо многокутника.
Навколо многокутника не завжди можна описати коло. Якщо ж це можна зробити, то центром такого кола є точка перетину серединних перпендикулярів до сторін многокутника.
 Многокутник називають описаним навколо кола, якщо всі його сторони дотикаються до кола. Коло при цьому називають вписаним у многокутник.
Многокутник називають описаним навколо кола, якщо всі його сторони дотикаються до кола. Коло при цьому називають вписаним у многокутник.
Вписати коло можна не в кожний многокутник. Якщо ж це можна зробити, то центром такого кола є точка перетину бісектрис внутрішніх кутів многокутника.
Інтерактивне спілкування з учнями
Учні отримують конверти (по одному на парту) з готовими паперовими моделями різних за видами многокутників та інших геометричних фігур (коло, еліпс тощо).
Практична робота
1. Серед наявних фігур виберіть шестикутник.
2. Накресліть у зашить фігуру, яка рівна обраній вами.
3. Назвіть многокутник.
4. Виміряйте його сторони й кути. Зробіть відповідні записи.
5. Знайдіть периметр многокутника.
6. Проведіть дві різні діагоналі та виміряйте їх. Зробіть відповідні записи.
Розв'язування задач
Задача 1. Накресліть чотирикутник, у якого два сусідні кути прямі, та побудуйте поруч з ним рівний йому чотирикутник.
Задача 2. Накресліть чотирикутник, у якого два протилежні кути тупі.
Задача 3. Чому дорівнює периметр многокутника АВСМР, якщо АВ=10 см, ВС=13 см, СМ=7 см, МР=9 см, АР=11 см?
Задача 4. Обчисліть периметр шестикутника, кожна з трьох сторін якого дорівнює 6 см, а кожна з трьох інших — 9 см.
Задача 5. У п'ятикутнику одна сторона дорівнює 17 см; друга на 8 см більша, ніж перша; третя в 3 рази менша, ніж сума першої й другої; четверта дорівнює п'ятій і на 5 см менша за другу. Обчисліть периметр п'ятикутника.
Задача 6. Проведіть олівцем по лініях фігури, не відриваючи його від паперу. Проводити двічі по лінії не можна.
Для кращого засвоєння учнями вивченого матеріалу можна провести математичний диктант (пропоную вибрати один з диктантів на вибір)
Математичний диктант №1
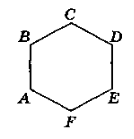 1. За рисунком назвіть:
1. За рисунком назвіть:
а) фігуру;
б) сторони фігури;
в) вершини фігури;
г) діагоналі фігури;
д) кількість діагоналей;
є) кількість кутів фігури;
ж) загальну кількість зовнішніх кутів фігури.
2.Закінчіть речення.
- Замкнена проста ламана, сусідні ланки не лежать на одній прямій, називається...
- Якщо кінці ламаної збігаються, то вона називається...
- Відрізок, які сполучає несусідні вершини многокутника, називається...
- Якщо ламана не має самоперетинів, то вона називається...
- Кут, суміжний із внутрішнім кутом многокутника при даній вершині, називається...
- n-кутник має ... діагоналей.
Математичний диктант №2
Закінчить речення: «Ламаною називається фігура, яка складається з…»
- Дано просту незамкнену ламану ABCDE. Виконайте її зображення. Назвіть усі вершини та ланки ламаної.
- Закінчить речення: « Многокутником називається..»
- Скільки всього діагоналей можна провести в опуклому п’ятикутнику ?
- За якою формулою обчислюється сума кутів опуклого многокутника ?
- Знайдіть суму кутів опуклого 12- кутника.
- Знайдіть градусну міру внутрішнього кута правильного 12-кутника.
- Чому дорівнює сума зовнішніх кутів 6-кутника?
- Чи залежить сума зовнішніх кутів многокутника від кількості його кутів?
- Знайдіть зовнішній кут правильного 9-кутника.
Робота в групах



![]()
![]()
![]()
Цікаві задачі для учнів неледачих
Задача про форму вічок бджолиних стільників
Чому бджоли використовують для побудови вічок на стільниках форму правильного шестикутника?

Розв'язання: З усіх правильних многокутників тільки трикутниками, квадратами й шестикутниками можна заповнити площину без прогалин і накладань. У цих випадках сума кутів, що сходяться в одній вершині, дорівнює 360°: для трикутника — 60°∙6; для квадрата — 90°∙4, для шестикутника — 120°∙3. Тому бджоли повинні були «вибрати» одну з цих фігур.
Порівняємо периметри цих многокутників за умови, що їхні площі рівні:
S3=S4=S6=S.
Для трикутника маємо: ![]() .
.
Для квадрата маємо: ![]() .
.
Для шестикутника маємо: ![]() .
.
![]() .
.
Отже, бджоли, не знаючи математики, інтуїтивно визначили, що правильний шестикутник має найменший периметр серед розглянутих фігур з рівною площею. Будуючи шестикутні вічка, бджоли найбільш ощадливо використовують площу усередині невеликого вулика й віск для виготовлення вічок.
Чому дорівнює периметр фігури?
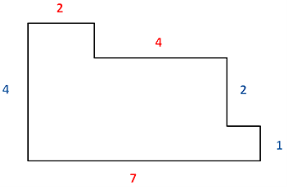
Додаткові завдання
Задача 1. Накресліть коло, впишіть у нього п҆ятикутник та опишіть навколо нього семикутник.
Задача 2. Усі внутрішні кути n-кутника дорівнюють по 135̊. Знайдіть n.
Задача 3. Як зміниться сума внутрішніх кутів опуклого многокутника, якщо кількість його сторін збільшити на дві?
Задача 4. Сума кутів опуклого n-кутника у k разів більша за суму кутів опуклого (n - 1)-кутника (k – натуральне число). Знайдіть k.
Розв҆язання задач підвищеної складності
№ 1014 (О. С. Істер Геометрія 8 клас)
Діагоналі опуклого чотирикутника розбивають його на чотири трикутники, периметри яких однакові. Визначте вид чотирикутника.
Розв҆язання: Розглянемо два випадки.
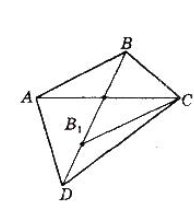 І випадок. Точка О – середина однієї діагоналі і не є серединою іншої діагоналі. Нехай АО = ОС, ВО < ОD. Позначимо на відрізку ОD точку В1 так, що ОВ1 = ОВ.
І випадок. Точка О – середина однієї діагоналі і не є серединою іншої діагоналі. Нехай АО = ОС, ВО < ОD. Позначимо на відрізку ОD точку В1 так, що ОВ1 = ОВ.
Оскільки ∆АВО = ∆СВ1О (за двома сторонами і кутом між ними: АО = СО, ВО = В1О, ![]() АОВ =
АОВ = ![]() СОВ1 як вертикальні), то АВ = СВ1.
СОВ1 як вертикальні), то АВ = СВ1.
За умовою Р∆АВО = Р∆СDО або АВ + АО + ОВ = ОВ1 +В1D + DС + СО. Звідси, враховуючи, що АО = ОС і ОВ = ОВ1, отримаємо, що АВ =В1D + DС або СВ1 = В1D + DC.
Але в ∆CB1D CB1 < B1D + DC. Отримали суперечність, отже перший випадок неможливий.
ІІ випадок.
Точка О не є серединою жодної з діагоналей. Нехай АО < ОС, ВО < ОD.
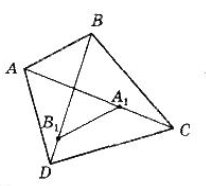 Позначимо точки А1 і В1 на відрізках ОС і ОD так, що ОА1 = ОА, ОВ1 = ОВ і розглянемо ∆ОА1В1.
Позначимо точки А1 і В1 на відрізках ОС і ОD так, що ОА1 = ОА, ОВ1 = ОВ і розглянемо ∆ОА1В1.
Оскільки ∆АОВ = ∆А1ОВ1, то АВ = А1В1.
За умовою Р∆АВО = Р∆СDО або АВ + АО + ОВ = ОВ1 +В1D + СА1 + А1О.
Звідки, враховуючи рівності ОА1 = ОА і ОВ = ОВ1,
отримаємо АВ = В1D + DC + CA1 або A1B1 = B1D + DC + CA1.
Але в чотирикутнику А1В1DC A1B1 < B1D1 + DC + CA1.
Отримали суперечність, значить випадок 2 також не може бути. Отже, АО = ОС, ВО = ОD, тому ABCD – паралелограм. А з умови Р∆АВО = Р∆СDО випливає, що АВ = ВС, тобто сусідні сторони паралелограма рівні. Тоді ABCD – ромб.
Відповідь: ромб.
Тема 2: Поняття площі многокутника. Площа прямокутника
Мета:
Навчальна складова:
- Сформулювати і довести теорему про площу многокутника та площу прямокутника;
- вчити учнів застосовувати формулу площі прямокутника до розв’язування задач.
Розвивальна складова:
- Розвивати пізнавальну діяльність учнів, логічне мислення, вміння шукати аналогії під час розв’язування задач за допомогою готових малюнків з умовами; комп’ютерну грамотність учнів.
Виховна складова:
Виховувати вміння слухати інших, співпереживати, формувати сприятливий моральний клімат.
Зміст теоретичного матеріалу
- Поняття площі многокутника.
- Основні властивості площі.
- Теорема про площу прямокутника та наслідок з теореми.
- Виведення формули на знаходження площ многокутника, прямокутника;
- Застосування формул до розв'язування задач.
Методичні поради
Під час викладання теоретичного матеріалу пропоную використати слайди презентації «Поняття площі многокутника. Площа прямокутника»
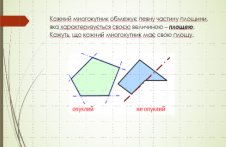
Опуклий та неопуклий многокутники
Кожний многокутник обмежує певну частину площини, яка характеризується своєю величиною – площею. Кажуть, що кожний многокутник має свою площу.
Площа многокутника
Площа многокутника — це величина тієї частини площини, яку займає многокутник.
Вимірювання площі пов'язано з порівнянням займаної частини площини з деякими одиницями вимірювання площі.
Одиниці вимірювання площі
 Для вимірювання площ ділянок на поверхні Землі користуються такими одиницями площ:
Для вимірювання площ ділянок на поверхні Землі користуються такими одиницями площ:
1 см2 = 100 мм2;
1 дм2 = 100 см2;
1 м2 = 100 дм2 = 10 000 см2;
1 ар = 100 м2;
1 га = 10 000 м2.
Площа квадрата
 Щоб знайти площу квадрата, треба його сторону помножити саму на себе, тобто підвести до квадрата.
Щоб знайти площу квадрата, треба його сторону помножити саму на себе, тобто підвести до квадрата.
Формула площі квадрата: S = a2, де a — сторона квадрата.
 Площа прямокутника
Площа прямокутника
Щоб знайти площу прямокутника, треба помножити його ширину на довжину.
Формула площі прямокутника: S = ab, де a і b – сторони прямокутника.
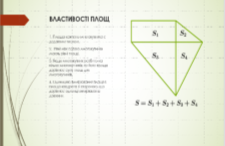 Властивості площ
Властивості площ
1. Площа кожного многокутника є додатним числом.
2. Рівні між собою многокутники мають рівні площі.
3. Якщо многокутник розбито на кілька многокутників, то його площа дорівнює сумі площ цих многокутників.
4. Одиницею вимірювання площі є площа квадрата зі стороною, що дорівнює одиниці вимірювання довжини.
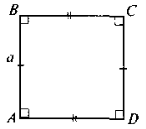
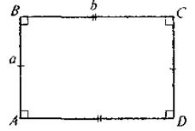
Теорема (про площу прямокутника). Площа S прямокутника зі сторонами a і b обчислюється за формулою
S = a * b
Доведення. Нехай ABCD – довільний прямокутник, у якого АВ = а, AD = b. Доведемо, що S = ab.
Якщо довжини відрізків АВ і AD є раціональними числами (цілими або дробовими), то існує відрізок такої довжини h, який можна відкласти ціле число разів і на відрізку АВ, і на відрізку AD.
D C
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a
1/n
A b 1/n B
Зведемо числа a і b до спільного знаменника п. Матимемо: ![]() ,
, ![]() . Тоді
. Тоді ![]() . Маємо a = ph, b = qh. Розіб’ємо відрізок АВ на р рівних частин завдовжки h, а AD – на q рівних частин завдовжки h. Через точки поділу проведемо прямі, паралельні сторонам прямокутника. Ці прямі розіб’ють увесь прямокутник на pq рівних між собою квадратів зі стороною
. Маємо a = ph, b = qh. Розіб’ємо відрізок АВ на р рівних частин завдовжки h, а AD – на q рівних частин завдовжки h. Через точки поділу проведемо прямі, паралельні сторонам прямокутника. Ці прямі розіб’ють увесь прямокутник на pq рівних між собою квадратів зі стороною ![]() (один з таких квадратів зафарбовано на малюнку). Оскільки одиничний квадрат вміщує рівно п2 квадратів зі стороною
(один з таких квадратів зафарбовано на малюнку). Оскільки одиничний квадрат вміщує рівно п2 квадратів зі стороною ![]() , то площа одного квадрата з такою стороною дорівнює
, то площа одного квадрата з такою стороною дорівнює ![]() . Площа прямокутника дорівнює сумі площ усіх квадратів. Маємо:
. Площа прямокутника дорівнює сумі площ усіх квадратів. Маємо:
![]()
Наслідок. Площа S квадрата зі стороною а обчислюється за формулою S = a2.
Для кращого засвоєння матеріалу доцільно запропонувати учням розглянути таблицю.
|
Площа. Властивості площ. Площа прямокутника |
|
|
Для площі S многокутника М справедливо, що: 1) S > 0. 2) Якщо M розбити на частини з площами S1 і S2, то S = S1 + S2. 3) Одиниця вимірювання площі в одиничних квадратах: 1 мм2 1 см2 і т. д. |
|
|
4) Якщо M1 = М2, то S1 = S2. 5) Якщо S1 = S2, то M1, і M2 — рівновеликі. 6) Нарис, а, б, в фігури є рівноскладеними. |
|
|
|
|
|
Многокутники, складені з однакової кількості відповідно рівних многокутників, називаються рівноскладеними. 7) Якщо M1, М2 — рівноскладені. То S1 = S2. |
|
|
Площа прямокутника |
|
|
|
|
|
Для ABCD — прямокутника АВ = а , ВС = b, S = ab. Для ABCD — квадрата (АВ = а), S = a2 |
|
З метою закріплення термінології (рівновеликі фігури, рівноскладені многокутники, властивість рівновеликих многокутників) та формул площ прямокутника і квадрата пропоную учням розв'язати усні вправи.
Виконання усних вправ
1. Площі двох многокутників рівні. Чи означає це, що самі многокутники також рівні?
2. Два прямокутники мають рівні периметри. Чи є вони рівновеликими?
3. Через середини двох протилежних сторін паралелограма проведено пряму. В якому відношенні вона ділить площу паралелограма?
4. Визначте, які з наведених тверджень правильні:
а) якщо діагоналі двох квадратів рівні, то ці квадрати рівновеликі;
б) два рівновеликі прямокутники рівні;
в) два рівновеликі квадрати рівні.
5. Сторона квадрата дорівнює меншій стороні прямокутника. Яка з цих фігур має більшу площу?
6. У трикутнику ABC проведено середні лінії. Вони поділили трикутник на 4 частини. Площа однієї з частин дорівнює 10. Чому дорівнюють площі інших частин?
7. Як розрізати на частини два рівних маленьких квадрати, щоб із цих частин можна було скласти один великий квадрат?
8. Визначте площу квадрата, описаного навколо кола, радіус якого R.
9. Квадрат і прямокутник мають рівні площі. Сторона квадрата дорівнює 12, а одна зі сторін прямокутника — 9. Чому дорівнює друга сторона прямокутника?
10. Периметр квадрата дорівнює 32. Чому дорівнює площа цього квадрата?
Розв'язування задач
Задача 1. Знайдіть площу прямокутника ABCD, якщо:
а) АВ = 9 см, ВС = 4 см;
б) АВ:ВС = 5:1, PABCD = 48 см;
в) AD = 12 см, АС = 13см.
Задача 2. Діагональ квадрата дорівнює ![]() м. Знайдіть площу квадрата.
м. Знайдіть площу квадрата.
Задача 3. Площа прямокутника дорівнює 128 см2. Знайдіть сторони прямокутника, якщо одна з них удвічі більша за іншу.
Задача 4. Бісектриса кута прямокутника ділить його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки розв'язків має задача?
Робота в малих групах
Даний метод інтерактивного навчання передбачає об҆єднання учнів у невеликі групи змішаного типу (слабкі, середні та сильні учні), для спільного виконання задачі.

![]()


![]()
![]()
Цікаві задачі для учнів неледачих
Задача 1. Скільки дошок потрібно, щоб настелити підлогу в кімнаті довжиною 7,5 м і шириною 5 м, якщо довжина дошки 6 м, а ширина 0,25 м?
Розв’язання: Поверхня підлоги має форму прямокутника, для знаходження площі, потрібно довжину помножити на ширину: S=7.5∙5=37.5(m2). Оскільки дошка теж має форму прямокутника, то її площа : S2=6∙0.25=1.5(m2). Для того, щоб дізнатись, скільки потрібно дошок, треба: k=S:S2 =37.5:1.5=25 (дошок). Відповідь: 25 дошок.
Задача 2. Довести, що із всіх прямокутників з однаковим периметром найбільшу площу має квадрат.
Розв’язання: Нехай квадрат ABCD та прямокутник AKLM, такі, що PABCD=PAKLM.
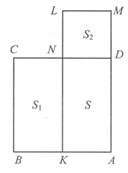
Порівняємо їх площі:
SABCD=S+S1; SAKLM=S+S2.
Порівняємо S1=KN∙KB i S2=DN∙DM.
Але KN>DN i KB=DM, тоді S1>S2.
Отже, SABCD>SAKLM, що й треба було довести.
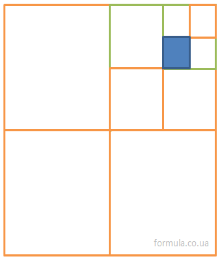
Задача 3. Яка частина квадрата зафарбована?
Задача 4. Задача царівни Дідони
Легенда розповідає, що фінікійська царівна Дідона, рятуючись від своїх ворогів, залишила рідне місто і в супроводі невеликого загону воїнів подалася у пошуках щастя на кораблі вздовж берегів Середземного моря. Обравши зручне місце на південному узбережжі Африки (нинішня Туніська затока), вона вирішила заснувати тут місто і звернулася до вождя місцевого племені з проханням дати їй ділянку землі, яку можна охопити «шкурою бика». Той відразу погодився.
Як Дідоні охопити найбільшу площу для заснування міста? Дідона повелася дуже хитро. Вона наказала розрізати шкуру бика на вузенькі смужки і зв’язати їх в один довгий ремінь. Оточивши ремнем досить значну територію, Дідона заснувала на ній місто Карфаген. Легенда датує цю подію 825 р. до н. е. Очевидно, Дідона розв’язала цікаву математичну задачу, яку часто називають її іменем.
Загальне формулювання такої задачі звучить так: «Серед усіх плоских фігур із заданим периметром знайти таку, що має найбільшу площу».
 ІСТОРИЧНА ДОВІДКА
ІСТОРИЧНА ДОВІДКА
Дещо про вимірювання площ було відомо геометрам багато тисячоліть тому.
2-3 тисячі років до н. е. вавилоняни вже вміли обчислювати площі прямокутника і трапеції у квадратних одиницях. Еталоном обчислення площ для них був квадрат зі стороною, що дорівнює одиниці довжини.
Для обчислення площ прямокутника, трикутника і трапеції давні єгиптяни 4000 років тому використовували ті самі формули, що й ми зараз.
У «Началах» Евклід не вживав термін «площа», оскільки під терміном «фігура» мав на увазі частину площини, що обмежена замкненою лінією, тобто площу. Евклід не подавав результат вимірювання площі різних фігур між собою, використовуючи термін «рівновеликі». Так, наприклад, у першій книзі «Начал» можна зустріти задачу 16: «Паралелограми, що знаходяться на різних основах і між тими самими паралельними, рівновеликі. Доведіть!».
Як і інші вчені, Евклід досліджував питання перетворення одних фігур в інші, їм рівновеликі. Так, наприклад, він розв҆язав задачу про побудову квадрата, рівновеликого даному многокутнику.
Тема 3. Розв’язування задач. Самостійна робота
Мета:
Навчальна складова:
- Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал до розв’язування задач.
Розвивальна складова:
- розвивати навички та вміння самостійної пізнавальної роботи, розвивати вміння аналізувати, робити висновки.
Виховна складова:
- Виховувати працелюбність, самостійність та вміння сконцентруватися.
Методичні поради
Урок можна провести методом розв҆язування доцільних завдань.
КРОСВОРД
По горизонталі:
- Чотирикутник, у якого всі кути прямі.
- Скільки вершин у многокутнику АВСD?
- Суміжні сторони прямокутника.
- Сума довжин усіх сторін многокутника.
- Кількість пар однакових сторін в прямокутнику.
По вертикалі:
- Сторони прямокутника рівні між собою.
- Прямокутник, в якого всі сторони рівні.
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
п |
р |
я |
м |
о |
к |
у |
т |
н |
и |
к |
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
2 |
ч |
о |
т |
и |
р |
и |
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
д |
|
3 |
п |
е |
р |
п |
е |
н |
д |
и |
к |
у |
л |
я |
р |
н |
і |
|
|
р |
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
4 |
п |
е |
р |
и |
м |
е |
т |
р |
|
|
|
т |
|
|
|
|
|
|
|
|
|
ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
д |
в |
і |
|
|
|
|
|
|
|
|
|
|
Самостійна робота (з подальшою взаємоперевіркою)
І варіант.
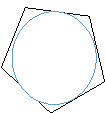
- (0,5 бали)На якому з малюнків зображено п҆ятикутник, описаний навколо кола.
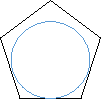
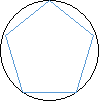
а б в г
2. (0, 5 бали) У якій з властивостей прямокутника допущено помилку:
а) протилежні сторони прямокутника мають однакову довжину, тобто вони рівні;
б) прилеглі сторони прямокутника завжди перпендикулярні;
г) всі чотири кути прямокутника прямі;
д) сума кутів прямокутника дорівнює 180 градусів;
- (За кожну відповідність 0,5 бала) Установити відповідність між сторонами фігур (1-4) і їх периметрами (А - Д).
|
1. |
Знайдіть периметр прямокутника, сторони якого дорівнюють 7 см і 4 см.
|
а |
24см |
|
32. |
Периметр квадрата 24см. Його сторона дорівнює |
б |
4 см |
|
43. |
Сторона прямокутника 5см, друга на 3см більша. Знайти периметр |
в |
24 см |
|
44. |
Відстань від точки перетину діагоналей квадрата до однієї з його сторін 3см. Знайти периметр квадрата |
г |
26 см |
|
|
|
д |
6 см |
4.(1 бал) В опуклому шестикутнику всі кути між собою рівні. Знайдіть ці кути.
5. (2 бали) Сторони прямокутника відносяться як 3:5, периметр дорівнює 32см. Знайти сторони прямокутника.
- (2 бали) Бісектриса кута А прямокутника АВСD ділить сторону ВС на частини 3см і 4см, починаючи від вершини В. Знайти периметр прямокутника.
7. (3 бали) Площа квадрата чисельно дорівнює периметру. Знайдіть сторону квадрата.
ІІ варіант.
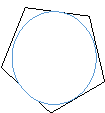
- (0,5 бала)На якому з малюнків зображено п҆ятикутник, вписаний в коло.
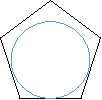
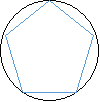
а б в г
2. (0, 5 бала) У якій з властивостей квадрата допущено помилку:
а) усі сторони квадрата мають однакову довжину, тобто вони рівні;
б) у квадрат завжди можна вписати коло;
г) діагоналі точкою перетину діляться у відношенні 1:2;
д) сума кутів прямокутника дорівнює 360 градусів;
3.(За кожну відповідність 0,5 бала) Установити відповідність між сторонами фігур (1-4) і їх периметрами (А - Д).
|
1. |
Знайдіть периметр прямокутника, сторони якого дорівнюють 5 см і 6 см.
|
а |
8см |
|
32. |
Периметр квадрата 32см. Його сторона дорівнює |
б |
24 см |
|
43. |
Сторона прямокутника 5см, друга на 2см більша. Знайти периметр |
в |
32 см |
|
44. |
Відстань від точки перетину діагоналей квадрата до однієї з його сторін 2см. Знайти периметр квадрата |
г |
6 см |
|
|
|
д |
16 см |
4.(1 бал) В опуклому восьмикутнику всі кути між собою рівні. Знайдіть ці кути.
5. (2 бали) Сторони прямокутника відносяться як 4:6, периметр дорівнює 40см. Знайти сторони прямокутника.
6. (2 бали) Бісектриса кута А прямокутника АВСD ділить сторону ВС на частини 4см і 5см, починаючи від вершини В. Знайти периметр прямокутника.
7. (3 бали) Площа квадрата дорівнює S см2. Знайдіть периметр квадрата.
Додаткові завдання
№ 1. Точка перетину діагоналей прямокутника розташована від більшої сторони на 5 см ближче, ніж від меншої сторони. Знайдіть сторони прямокутника, якщо його периметр дорівнює 44 см.
№ 2. Доведіть, що прямокутник, діагоналі якого перпендикулярні, є квадратом.
№ 3. На діагоналі АС квадрата ABCD позначено точки К і М так, що АК = СМ. Доведіть, що BMDK - ромб.
Тема 4. Площа паралелограма.
Мета:
Навчальна складова:
- Сформулювати і довести теорему про площу паралелограма;
- вчити учнів застосовувати формулу площі паралелограма до розв’язування задач.
Розвивальна складова:
- розвивати навички мислення, спостережливість, вміння шукати аналогії під час розв’язування задач за допомогою готових малюнків з умовами; комп’ютерну грамотність учнів.
Виховна складова:
- Виховувати інтерес до геометрії, графічну культуру учнів, математичне мовлення.
Зміст теоретичного матеріалу
- Теорема про площу паралелограма;
- Виведення формули на знаходження площі паралелограма
- Застосування формули до розв'язування задач.
Методичні поради
Вивчення даної теми пропоную розпочати з інтерактивного спілкування, з метою сформулювати теорему площі паралелограма разом з учнями на основі завдань, виконаних у практичній роботі.
Практична робота
Учні отримують конверти (по одному на парту) з готовими паперовими моделями паралелограмів та ножиці.
Завдання:
1. За допомогою ножиць і моделі паралелограма зробити фігуру, площу якої ви вмієте знаходити.
2. Як знайти площу?
3. Маркером наведіть ті сторони, які треба помножити.
4. Складіть знову паралелограм і дайте відповіді на питання: чи зміниться площа фігури? Згідно якої вивченої нами властивості можна це стверджувати?
5. Чим для паралелограма є зафарбовані сторони?
6. Спробуйте сформулювати теорему про площу паралелограма.
Теорема (про площу паралелограма). Площа паралелограма дорівнює добутку його сторони на висоту, проведену до цієї сторони.
Доведення
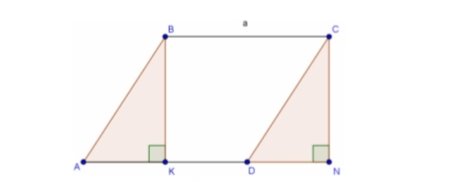
- Проведемо висоти паралелограма ВК (ВК┴АD) i CN (CN┴АD).
- Розглянемо ∆АВК і ∆DCN.
- ∆АВК = ∆DCN (за двома сторонами): АВ = DC, як сторони паралелограма; ВК = CN, як висоти.
- Якщо ∆АВК = ∆DCN, то їх площі також рівні.
- Площа паралелограма ABCD дорівнює площі прямокутникаKBCN, тобто S = BC * BK = aha.
Теорему доведено.
Наслідок (із формули площі паралелограма)
Запишемо площу паралелограма двома способами:
S = aha i S = bhb;
aha = bhb;
![]()
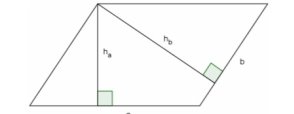
Висновок. Сторони паралелограма обернено пропорційні його відповідним висотам.
Розв҆язування задач
Задача 1. Сторона паралелограма дорівнює 6 см, висота, проведена до цієї сторони - 3 см. Знайдіть площу паралелограма.
Задача 2. Діагональ паралелограма завдовжки 5 см перпендикулярна до сторони паралелограма, що дорівнює 6 м. Знайдіть площу паралелограма.
Задача 3. Сума кутів паралелограма дорівнює 1300. Знайти найбільший кут паралелограма.
Задача 4. Периметр паралелограма дорівнює 84 см, а сума двох його сторін – 58 см. Знайти меншу сторону паралелограма.
Задача 5. Бісектриса гострого кута паралелограма поділяє сторону на відрізки завдовжки 7 см і 10 см, починаючи від вершини тупого кута. Знайти периметр паралелограма.
Розв҆язання: Нехай маємо паралелограм ABCD, AB||DC і AD||BC, AК – бісектриса.
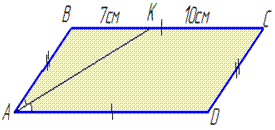
За умовою: BK = 7 см, КC = 10 см, тому маємо BC = BK + KC = 7 + 10 = 17 см. За властивістю паралелограма: AD = BC = 17 см. Оскільки AK – бісектриса, то ∠BAK = ∠KAD.
За ознакою паралельності прямих (AD||BC), як перетнуті січною AK, маємо ∠AKB=∠KAD. Тому ∠BAK=∠AKB. Звідси слідує (за теоремою), що ΔABK– рівнобедрений з основою AK і бічними сторонами AB і BK, тому (за означенням) AB=BK=7 см. За властивістю паралелограма: CD = AB = 7 см. Знайдемо периметр паралелограма (сума всіх його сторін): P = AB + BC + CD + AD = 2(AB + BC) = 2(7 + 17) = 48 см.
Задача 6. Сторони паралелограма дорівнюють 18 см і 30 см, а висота, яка проведена до більшої сторони, - 6 см. Знайти іншу висоту паралелограма.
Розв҆язання: 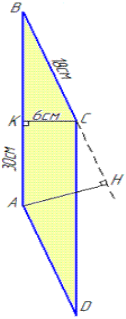 Виконаємо побудову паралелограма у якого AB||DC і AD||BC, CK ⊥AB, AH ⊥BC,
Виконаємо побудову паралелограма у якого AB||DC і AD||BC, CK ⊥AB, AH ⊥BC,
Де CK і AH – висоти паралелограма, опущені на сторони AB і BC, відповідно
За умовою: AB=30 см, BC=18 см, CK=6 см. Площа паралелограма дорівнює добутку сторони на висоту, проведену до неї. Обчислимо площу паралелограма ABCD: SABCD=AB•CK=30•6=180 cм2. Але площу паралелограма можна обчислити також за формулою: SABCD=BC•AH, звідси ![]()
Інтерактивна вправа «Дай відповіді на знаки питання»
|
S = ab ?
S =
?
|
|
?
?
|
Цікаві задачі для учнів неледачих
Задача 1. У басейні дуже паралелограмної форми плаває Гіпотенузопотам. Він плаває з кута в кут по діагоналі, яка утворює зі сторонами басейну кути 90̊ і 30̊. Обчисліть довжини сторін басейну, якщо його периметр дорівнює 180 м.


Задача 2. Ось Паралелозавр. Він бігав по периметру паралелограмної клітки, одна сторона якої менша за периметр на 24 м, а друга – на 33 метри. Визначте периметр клітки.

Задачі підвищеної складності
№ 1. Периметр паралелограма більший від однієї з його сторін на 23 см і більший на 19 см від іншої його сторони. Знайти периметр паралелограма.
Розв҆язання: Побудуємо паралелограм зі сторонами a см і b см.
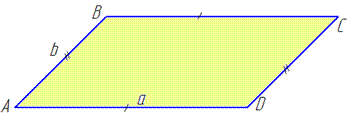
Оскільки протилежні сторони паралелограма рівні (за властивістю), то його периметр визначаємо через подвоєну суму сусідніх сторін:
P=2a+2b.
За умовою задачі, маємо:
2a+2b-a=23 (*) і
2a+2b-b=19 (**).
Отримали систему двох рівнянь з двома невідомими:
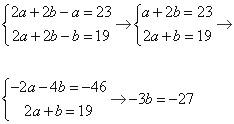
Звідси b=9 і a=5.
Знаючи сторони, без проблем знаходимо периметр паралелограма за формулою:
P=2a+2b=2•5+2•9=28 см
№ 2. Одна з діагоналей паралелограма дорівнює 6 √6 і утворює зі стороною паралелограма кут 600. Знайти іншу діагональ, якщо вона утворює з тією ж стороною кут 450.
Розв҆язання: Маємо паралелограм ABCD, AB||CD і AD||BC, AC=6 √6, ∠CAD=60, ∠BDA=45, де AC і BD – діагоналі паралелограма, які перетинаються в точці O.
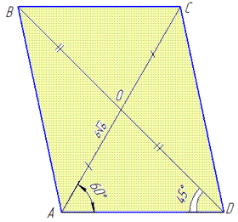 Тоді, за властивістю паралелограма
Тоді, за властивістю паралелограма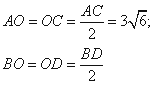
Розглянемо трикутник AOD, у якого![]()
За теоремою синусів знайдемо сторону OD: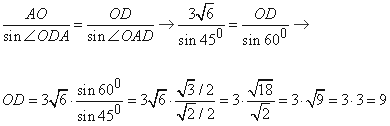
Знайдемо діагональ BD паралелограма ABCD: оскільки BO=OD=BD/2=9, то BD=2•OD=2•9=18.
Тема 5.Площа трикутника
Мета:
Навчальна складова:
- Сформулювати і довести теорему про площу трикутника, у тому числі прямокутного, рівностороннього;
- вчити учнів застосовувати формули площ трикутників до розв’язування задач;
Розвивальна складова:
- розвивати творче мислення, спостережливість, вміння шукати аналогії під час розв’язування задач за допомогою готових малюнків з умовами.
Виховна складова:
- Виховувати старанність, охайність та графічну культуру учнів.
Зміст теоретичного матеріалу
- Теорема про площу трикутника та наслідки з неї;
- Виведення формули на знаходження площі трикутника, у тому числі прямокутного, рівностороннього;
- Застосування формул до розв'язування задач.
Методичні поради
Під час викладання теоретичного матеріалу пропоную використати слайди презентації «Площа трикутника»
 Трикутник у евклідовій системі –геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що їх сполучають.
Трикутник у евклідовій системі –геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що їх сполучають.
Трикутник є многокутником і 2-симплексом. В евклідовій геометрії трикутник однозначно задає площину. Всі трикутники двовимірні.
 Види трикутників: рівносторонній, рівнобедрений, прямокутний, різносторонній
Види трикутників: рівносторонній, рівнобедрений, прямокутний, різносторонній
 Ейлерова діаграма видів трикутників
Ейлерова діаграма видів трикутників
 Рівносторонній трикутник — трикутник, усі сторони якого рівні.
Рівносторонній трикутник — трикутник, усі сторони якого рівні.
В Евклідовій геометрії всі три кути рівностороннього трикутника також рівні. Тому рівносторонні трикутники є правильними многокутниками і мають назву правильних.
Усі кути правильного трикутника дорівнюють 60°
Площа рівностороннього трикутника:
S = ![]()
 Рівнобедрений трикутник - трикутник, в якому дві сторони рівні між собою. Рівні сторони називаються бічними, а остання — основою.
Рівнобедрений трикутник - трикутник, в якому дві сторони рівні між собою. Рівні сторони називаються бічними, а остання — основою.
За означенными, правильний трикутник також є рівнобедреним, але обернене твердження не є правильним.
Площа трикутника може бути обчислена за формулами:
![]() ;
; ![]()
Прямокутний трикутник — трикутник, один із кутів якого прямий.
Прямокутний трикутник займає особливе місце в планіметрії, оскільки для нього існують прості співвідношення між сторонами і кутами.
 Сторони прямокутного трикутника мають власні назви. Дві сторони, що утворюють прямий кут називаються катетами, а третя сторона — гіпотенузою. Традиційно катети позначаються літерами a та b, а гіпотенуза — літерою c. За теоремою Піфагора можна знайти будь-яку сторону прямокутного трикутника, якщо відомі дві інші сторони.
Сторони прямокутного трикутника мають власні назви. Дві сторони, що утворюють прямий кут називаються катетами, а третя сторона — гіпотенузою. Традиційно катети позначаються літерами a та b, а гіпотенуза — літерою c. За теоремою Піфагора можна знайти будь-яку сторону прямокутного трикутника, якщо відомі дві інші сторони.
За теоремою Піфагора квадрат гіпотенузи дорівнює сумі квадратів катетів.
![]()
Площа прямокутного трикутника:
![]()
 Різностороннім називається трикутник, у якого всі сторони мають різну довжину. Внутрішні кути різностороннього трикутника різні.
Різностороннім називається трикутник, у якого всі сторони мають різну довжину. Внутрішні кути різностороннього трикутника різні.
Площа трикутника:
![]()
Площа трикутника може бути показана як половина площі паралелограма, який має таку саму основу та висоту.
Неплощинні трикутники — це трикутники, що знаходяться не на (плоскій) площині. Прикладом такого трикутника в неевклідовій геометрії є сферичний трикутник, що вивчається в сферичній геометрії та гіперболічний трикутник в гіперболічній геометрії.
 Точки і лінії пов’язані з трикутником
Точки і лінії пов’язані з трикутником
Додаткові відомості:
- Будь-яка медіана трикутника поділяє його на два рівні за площею трикутники(рівновеликі трикутники).
- Три медіани трикутника перетинаються в одній точці і при цьому утворюють шість трикутників, площі яких рівні.
- Якщо основи двох трикутників рівні, то відношення площ цих трикутників дорівнює відношенню їх висот, і навпаки якщо у двох трикутників висоти рівні, то відношення їх площ дорівнює відношенню їх основ.

Створення проблемної ситуації
Для створення ситуації, що допоможе учням зрозуміти ідею доведення теореми про площу трикутника, варто запропонувати задачу.
Задача. На дошці зображено дві фігури: паралелограм ABCD і трикутник MNK такі, що AD = МК, і висоти проведені до цих сторін (ВН, NF), також рівні (див. рис).
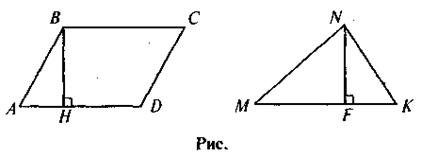
Площа паралелограма відома. Як знайти площу трикутника?
Пошук відповіді на питання задачі допоможе учням усвідомити:
- існування протиріччя між набутими знаннями та змістом задачі (учні вміють знаходити площі прямокутника і паралелограма, а за змістом задачі слід знайти площу трикутника);
- зміст задачі містить «підказку» — обчислення площі трикутника слід якось пов'язати з обчисленням площі паралелограма.
Теорема (про площу трикутника). Площа трикутника дорівнює половині добутку його сторони на висоту, проведену до цієї сторони.
Доведення
 В D
В D
А С
Н
Нехай АВС – довільний трикутник, ВН – його висота. Доведемо, що ![]() .
.
- Проведемо через вершину В пряму, паралельну АС, а через вершину С – пряму, парлельну АВ. Одержимо паралелограм АВСD.
-
∆АВС =∆DВС (за трьома сторонами). Тому S АВСD = 2 S АВС, звідки S АВС =
 SАВСD,
SАВСD,
-
Оскільки SАВСD = АС*ВН, то S АВС =
 АС*ВН.
АС*ВН.
У загальному вигляді формулу площі трикутника S можна записати так:
![]() a
a
де а – сторона трикутника, ha – висота, проведена до неї.
Наслідок 1. Площа прямокутного трикутника дорівнює половині добутку катетів.
Наслідок 2. Якщо сторона одного трикутника дорівнює стороні другого, то площі таких трикутників відносяться як їх висоти, проведені до цих сторін.
Наслідок 3. Якщо висота одного трикутника дорівнює одній з висот другого трикутника, то площі цих трикутників відносяться як сторони, до яких проведено ці висоти.
Виконання усних вправ
1.Площа трикутника ABC дорівнює S. Чому дорівнює площа паралелограма ABCD, три вершини якого збігаються з вершинами даного трикутника?
2. За якою формулою доцільно обчислювати площу прямокутного трикутника, якщо відомі:
а) довжини гіпотенузи і проведеної до неї висоти;
б) довжини двох катетів?
3. Два рівновеликі трикутники мають рівні висоти. Чи означає це, що основи даних трикутників також рівні?
4. Доведіть, що більшій стороні трикутника завжди відповідає менша висота.
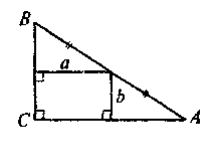
5. Яка площа трикутника ABC на рисунку?
6. У паралелограмі провели діагоналі. Чи рівні площі всіх утворених чотирьох трикутників?
Розв’язування задач
Задача 1. Дано три трикутники: гострокутний, прямокутний і тупокутний. Який з цих трикутників має найбільшу площу, якщо вони мають по дві відповідно рівні сторони, які утворюють ці кути?


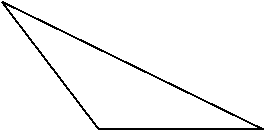
Розв҆язання: ![]() . Оскільки найбільше значення sin 90̊ = 1, то
. Оскільки найбільше значення sin 90̊ = 1, то ![]() – площа прямокутного трикутника.
– площа прямокутного трикутника.
Задача 2. Дослідити чи можливо це?
5 14
15
Розв҆язання: 1. За формулою Герона знайдемо площу трикутника ![]() ,
,
S = 84 см2.
-
Оскільки
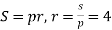 (см)
(см)
Отже, коло, радіус якого 5 см, у такий трикутник вписати неможливо.
Задача 3. Дослідити як зміниться площа трикутника, якщо всі його сторони збільшити у два рази.
Розв҆язання: Нехай даний трикутник має сторони a, b, c. Його площа рівна S. Якщо всі сторони збільшити у два рази, тобто подіяти на трикутник перетворенням подібності з коефіцієнтом 2, то довжини стануть рівними 2a, 2b, 2c. Площа трикутника S зміниться на k2S. Отже, площа збільшиться у 4 рази.
Для закріплення та кращого засвоєння учнями вивченого матеріалу пропоную розгадати кросворд або провести тестування (на вибір вчителя).
КРОСВОРД
|
|
|
1 |
г |
о |
с |
т |
р |
о |
к |
у |
т |
н |
и |
й |
|
|
|
|
|
2 |
п |
р |
о |
с |
т |
а |
|
|
|
|
|
|
|
|
3 |
є |
г |
и |
п |
е |
т |
с |
ь |
к |
и |
й |
|
4 |
п |
р |
я |
м |
о |
к |
у |
т |
н |
и |
й |
|
|
|
|
|
|
|
|
5 |
к |
у |
т |
|
|
|
|
|
|
|
|
|
|
|
6 |
к |
о |
т |
а |
н |
г |
е |
н |
с |
|
|
|
|
|
7 |
р |
і |
в |
н |
о |
в |
е |
л |
и |
к |
і |
|
|
|
|
|
8 |
о |
д |
и |
н |
и |
ц |
я |
|
|
|
|
|
|
9 |
б |
і |
с |
е |
к |
т |
р |
и |
с |
а |
|
|
|
- Якщо всі кути трикутника рівні між собою, то такий трикутник…(гострокутний).
- Геометрична фігура, яку можна розбити на нескінченне число плоских трикутників називається… (проста).
- Прямокутний трикутник, сторони якого відносяться як 3:4:5 називається… (єгипетський).
- Якщо один кут трикутника дорівнює сумі двох інших кутів, то такий трикутник…(прямокутний).
- Лупа не збільшує геометричну фігуру…(кут).
- Відношення косинуса кута до його синуса називається…(котангенс).
- Трикутники, які мають рівні площі називаються…(рівновеликі).
- Функція синус може набувати найбільшого значення…(одиниця).
- Центр кола, вписаного в трикутник, лежить у точці перетину…(бісектрис)
Тестові завдання
 Варіант І
Варіант І
1. Назвіть формулу площі прямокутника зі сторонами а і b
а) ![]() ; б)
; б) 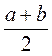 ; в) а2 + b2; г) ab.
; в) а2 + b2; г) ab.
2. Знайдіть площу ромба ABCD, якщо АС = 5 см, BD = 8 см.
а) 20 см2; б) 40 см2; в) 10 см2; г) 13 см2.
3. За даними рисунка знайдіть площу трикутника ABC.
а) 42; б) 84; в) 13; г) 21.
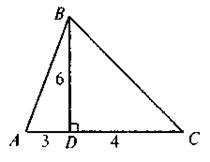
4. Знайдіть площу прямокутника зі стороною 5 м і діагоналлю 13 м.
а) 60 см2; б) 60 м2; в) 65 м2; г) 156 м2.
5. Дві сторони трикутника дорівнюють 8 см і 12 см, а висота, проведена до меншої з них, — 3 см. Знайдіть висоту, проведену до більшої сторони.
а) 4 см; б) 2 см; в) 4.5 см; г) 10 см.
6. Знайдіть площу ромба зі стороною 12 см і гострим кутом 30°.
а) 144 см2; б) 36см2; в) ![]() см2; г) 72 см2.
см2; г) 72 см2.
Варіант 2
1. Назвіть формулу площі квадрата зі стороною а.
а) 2а2; б) 4а; в) а2; г) 4а2.
2. У паралелограмі ABCD до сторони AD проведено висоту ВК. Знайдіть площу паралелограма, якщо ВС = 8 см, ВК = 5 см.
а) 20 см2; б) 40 см2; в) 80 см2; г) 13 см2.
3. За даними рисунка знайдіть площу три кутника ABC.
а) 30; б) 60; в) 15; г) 11.
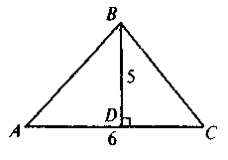
4. Знайдіть площу прямокутного трикутника з катетом 15 м і гіпотенузою 17 м.
а) 127,5 м2; б) 60 м2; в) 120 м2; г) 60 см2.
5. Сторони паралелограма дорівнюють 12 см і 16 см, а менша висота – 3 см. Знайдіть більшу висоту паралелограма.
а) 4 см; б) 2,25 см; в) 6 см; г) 14 см.
6. Знайдіть площу паралелограма зі сторонами 8 м і 12 м та гострим кутом 30°.
а) 48 м2; б) 96 м2; в) 24 м2; г) інша відповідь.
Після закінчення роботи — перевірка і корекція.
Додаткові завдання
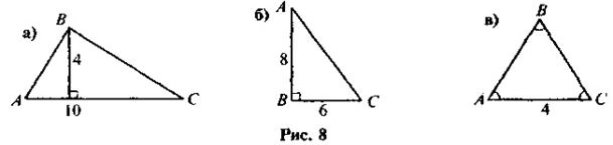
Задача 1.За даними рисунка 8 знайдіть площу трикутника ABC.
Задача 2. Знайдіть площу:
а) рівнобедреного трикутника з основою 10 см і бічною стороною 13 см;
б) трикутника ABC, в якому АВ = 17 см, а висота ВН ділить сторону АС на відрізки АН = 8 см і НС = 2 см.
Задача 3. Площа трикутника дорівнює 72 см2. Знайдіть периметр трикутника, якщо його висоти дорівнюють 9 см, 12 см і 24 см.
Задача 4. Знайдіть площу ромба, діагоналі якого дорівнюють 8 м і 20 м.
Задача 5. Знайдіть площу:
а) трикутника ABC з висотою ВН , якщо АВ= 13 см, ВС = 15 см, ВН = 12 см, а точка Н лежить на відрізку АС;
б) прямокутного трикутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см;
в) рівностороннього трикутника з висотою2 ![]() см.
см.
Задача 6. На рисунку 9 подано одиничний квадрат. Знайдіть площу заштрихованої фігури.
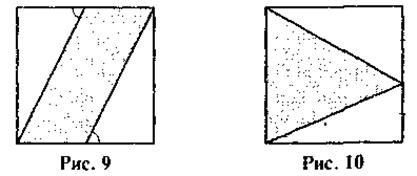
Задача 7. На рисунку 10 подано одиничний квадрат. Знайдіть площу заштрихованої фігури.
Тема 6. Площа трапеції
Мета:
Навчальна складова:
- Сформулювати і довести теорему про площу трапеції та наслідок з неї;
- вчити учнів застосовувати формулу площі трапеції до розв’язування задач;
Розвивальна складова:
- Розвивати в учнів логічне мислення, вміння аналізувати і робити висновки
Виховна складова:
- Виховувати дисципліну, звичку до систематичної розумової праці, культуру математичних висловлювань.
Зміст теоретичного матеріалу
- Теорема про площу трапеції та наслідок з неї
- Виведення формули на знаходження площі трапеції;
- Застосування формули до розв'язування задач.
Методичні поради
Під час викладання теоретичного матеріалу пропоную використати слайди презентації «Площа трапеції»
 Трапеція — це чотирикутник, дві протилежні сторони якого паралельні.
Трапеція — це чотирикутник, дві протилежні сторони якого паралельні.
Паралельні сторони називаються основами трапеції (сторони AB та DC на малюнку). Інші сторони називаються бічними сторонами (сторони AD та CB).
Окремі види трапеції
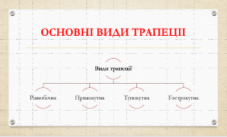

Площа трапеції рівна добутку півсуми основ на висоту
Середня лінія трапеції рівна півсумі основ, тому формулу площі можна перефразувати
Площа трапеції 
Якщо задано діагоналі трапеції та кут між ними
І ВИПАДОК
Якщо трапеція рівнобічна, і в неї діагоналі перпендикулярні, то площа такої трапеції буде рівна квадрату її висоти. S =h²


ІІ ВИПАДОК
Якщо трапеція рівнобічна, то площа трапеції рівна сумі коренів із площ утворених подібних трикутників піднесена до квадрату.
ІІІ ВИПАДОК
Якщо трапеція прямокутна, і в неї можна вписати коло, то площа такої трапеції буде рівна добутку її основ.

ІV ВИПАДОК
 Якщо трапеція рівнобічна, і в неї можна вписати коло, то площа такої трапеції буде рівна добутку півсуми основ, на корінь із добутку основ.
Якщо трапеція рівнобічна, і в неї можна вписати коло, то площа такої трапеції буде рівна добутку півсуми основ, на корінь із добутку основ.

V ВИПАДОК
Якщо трапеція рівнобічна, і в неї можна вписати коло, то площа цієї трапеції буде рівна добутку подвоєної суми відрізків на які ділить бічну сторону вписане коло, на корінь із їх добутку.
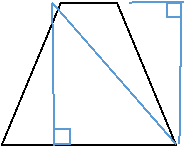
Теорема (про площу трапеції). Площа трапеції дорівнює добутку півсуми її основ на висоту.
 B C N
B C N
А К D
Доведення
Нехай АВСD – довільна трапеція з основами АD і ВС, ВК – її висота. Доведемо, що площу трапеції S можна знайти за формулою:
![]() .
.
- Діагональ BD розбиває трапецію на два трикутники ABD i BDC. Тому S = SABD +SBDC.
-
ВК – висота трикутника ABD, тому SABD =
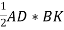 .
.
-
Проведемо у трапеції висоту DN, вона є і висотою трикутника BDC, тому SBDC =
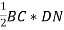 .
.
-
DN = BK (як висота трапеції). Отже, S = SABD +SBDC =
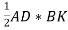 +
+ 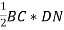 =
= 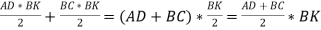 .
.
У загальному вигляді формулу площі трапеції S можна записати так:
![]() ,
,
де a і b – основи тапеції, h – її висота.
Наслідок. Площа трапеції дорівнює добутку її середньої лінії на висоту.
Для перевірки основних понять з теми «Трапеція» доцільно запропонувати учням розгадати кросворд.
КРОСВОРД
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
3 |
б |
і |
ч |
н |
і |
|
|
|
|
|
|
|
|
|
о |
|
|
|
1 |
|
|
|
|
|
4 |
в |
и |
с |
о |
т |
а |
|
|
|
|
|
и |
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
5 |
с |
е |
р |
е |
д |
н |
я |
|
Питання
1. Чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні. (Трапеція)
2. Як називаються паралельні сторони трапеції? (Основи)
3. А непаралельні? (Бічні)
4. Перпендикуляр, опущений з будь-якої точки прямої, яка містить одну з основ, на пряму, яка містить другу основу. (Висота)
5. Лінія, яка сполучає середини бічних сторін трапеції. (Середня)
Інтерактивне спілкування з учнями
„Асоціативний кущ”
Ключовим словом „Асоціативного куща” є трапеція. Учні по черзі на гілках „куща” записують слова, фрази , що пов’язані з ключовим словом. Далі учні розкривають зміст кожної гілки.





![]()


![]()

![]()
![]()





Завдання на кмітливість
1) Одного разу Петрик П'яточкін склав трапецію із чотирьох прямокутних трикутників. Чи зможете ви повторити його досягнення? «покращити» (тобто скласти трапецію з меншої кількості прямокутних трикутників)? Що спільного мають усі трикутники в кожному із зображених випадків?
2) Який із випадків можливий для будь-якої трапеції?
Розв'язуючи завдання, учні можуть прийти до конфігурацій, зображених на малюнку
Виконання усних вправ
1. Дві рівновеликі трапеції мають рівні висоти. Чи означає це, що основи даних трапецій також відповідно рівні?
2. Чи може діагональ трапеції ділити її на два рівновеликі трикутники? Відповідь обґрунтуйте.
3. Дано: ABCD — трапеція (BC || AD). Знайдіть S, якщо:
а) ВС = 2 см; AD = 10 см; h = 5 см;
б) BC + AD = 16 см; h = 6 см;
в) середня лінія дорівнює 10 см; висота 5 см;
г) r = 5 см; AB + CD = 18.
Розв’язування письмових задач
Задача 1. Знайти площу трапеції, основи якої 12см та 18см, а висота 6 см.
Задача 2. Основи трапеції 9см та 11см, а її площа – 150см2. Знайдіть висоту трапеції .
Задача 3. Площа трапеції дорівнює 96см2, а її висота – 8см. Знайдіть основи трапеції, якщо їх різниця дорівнює 9 см.
Задача 4. Бісектриса тупого кута трапеції, що дорівнює 150°, поділяє більшу основу на відрізки 12см та 8см. Знайдіть площу трапеції, якщо її менша основа дорівнює 14см.
Задача 5. Знайдіть площу рівнобічної трапеції, основи якої 7см та 25 см, а діагональ перпендакулярна до бічної сторони.
Задача 6. В трапеції ABCD AB = 26 cм, CD = 32см – бічні сторони. Кут CDA дорівнює 30![]() Знайдіть площу трапеції, якщо відомо, що в неї можна вписати коло.
Знайдіть площу трапеції, якщо відомо, що в неї можна вписати коло.
Виконання практичного завдання
Уявіть, що ви будівельники. Як знайти довжину паркану (тобто периметр трапеції ABXC), яким огороджено дитячий майданчик, якщо вершина X недоступна та купою піску частково присипано сторони BX і XC (див. рис.)? Ви повинні поміркувати та розв'язати цю проблему. (Учні працюють у парах.)
Розв'язання:
- Поділити сторону AB на три рівні частини та провести прямі KK1, MM1 паралельно AC.
- Виміряти M1C, тоді XC=3M1C
- Виміряти AC, MM1 та знайти BX.
 В Х
В Х
К К1
М М1
А С
Для закріплення та перевірки вивченого матеріалу з теми «Площа трапеції» можна використати тестові завдання.

Тестові завдання
- Чи існує трапеція, у якої лише один кут прямий?
а) так; б) ні; в) неможна визначити;
2. Визначте вид трикутника, у якого дві середні лінії перпендикулярні і рівні
а) рівнобедрений прямокутний;
б) рівнобедрений тупокутний;
в) рівнобедрений гострокутний;
3. Чи існує трапеція, у якої три кути прямі?
а) так; б) ні; в) неможна визначити;
4. Визначте вид трикутника, у якого дві середні лінії рівні і перетинаються під кутом 60°.
а) різносторонній; б) рівнобедрений; в) рівносторонній;
5. Чи існує трапеція, у якої два протилежні кути гострі?
а) так; б) ні; в) неможна визначити;
6. Чи можуть середні лінії трикутника відноситись як 1:2:3?
а) так; б) ні; в) неможна визначити;
7. Чи існує трапеція, у якій два протилежні кути тупі?
а) так; б) ні; в) неможна визначити;
8. Чи може середня лінія трикутника бути вдвічі більшою за кожну з двох інших середніх ліній?
а) так; б) ні; в) неможна визначити;
Тема 7. Розв’язування задач. Самостійна робота
Мета:
Навчальна складова:
- Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал , до розв’язування задач,
Розвивальна складова:
- розвивати навички та вміння самостійної пізнавальної роботи,
- розвивати вміння аналізувати, робити висновки.
Виховна складова:
- Виховувати графічну культуру, старанність та самостійність.
Методичні поради
Урок можна провести методом розв҆язування доцільних завдань.
Бліц опитування (закінчити речення)
- Чотирикутник, у якого кожні дві протилежні сторони паралельні називають …..
- У паралелограма протилежні сторони….
- У паралелограма протилежні кути ….
- Перпендикуляр опущений з будь-якої точки прямої, яка містить сторону паралелограма, на пряму, що містить протилежну сторону, називається….
- Сума будь-яких двох сусідніх кутів паралелограма дорівнює…
- Якщо в чотирикутнику діагоналі точкою перетину діляться пополам, то цей чотирикутник називається….
- Прямокутником називається паралелограм, у якого ….
- В прямокутника діагоналі ….
- Якщо один з кутів паралелограма прямий, то цей паралелограм називається….
- Паралелограм у якого всі сторони рівні називається….
- Діагоналі ромба….
- Прямокутник у якого всі сторони рівні називається ….
- Паралелограм у якого діагональ є бісектрисою його кута називають….
- Діагоналі в квадрата ….
- Геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з’єднують ці точки ….
- Трикутник, який має дві рівні сторони ….
- Трикутник, у якого є прямий кут ….
- Площа трикутника дорівнює ….
- Якщо сторона одного трикутника дорівнює стороні другого, то площі таких трикутників відносяться як ….
- Відрізок, що сполучає середини бічних сторін трапеції - ….
- В трапецію можна вписати коло, якщо сума основ трапеції дорівнює….
- Точка перетину діагоналей трапеції, точка перетину продовжень її бічних сторін та середини основ лежать ….
- Площа трапеції дорівнює добутку її півсуми….
- Трапеція, у якої бокові сторони рівні ….
- Трапеція, у якої одна із бокових сторін перпендикулярна основа ….
- Добуток середньої лінії трапеції на її висоту ….
Самостійна робота
Варіант І
1.(0,5 бала) Вибрати невірне твердження.
а) Многокутник опуклий, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону;
б) рівні фігури мають рівні площі;
в) сума кутів опуклого n-кутника дорівнює 360°;
г) площа паралелограма дорівнює добутку його сторони на висоту, проведену до цієї сторони.
2.(0,5 бала) Скільки діагоналей в опуклого п’ятикутника?
а) 4; б) 5; в) 6; г) 8.
3. (0,5 бала) Сума внутрішніх кутів опуклого шестикутника
а) 360°; б) 540°; в) 720°; г) 1080°.
4.(0,5 бала) Центр описаного навколо многокутника кола лежить на перетині
а) бісектрис;
б) висот;
в) діагоналей;
г) серединних перпендикулярів.
- (0.5 бала) Діагоналі ромба 6см і 8см. Його площа
а) 48см2; б) 14см2; в) 28см2; г) 24см2.
6. (0,5 бала) Яка з формул є формулою для обчислення площі трикутника?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
7. ( 1 бал) У квадрат, площа якого 64см2 вписано коло. Чому дорівнює радіус даного кола?
а) 16см; б) 8см; в) 32см; г) 4см.
8.( 1 бал) В опуклому многокутнику сума його внутрішніх кутів дорівнює 2340°. Знайти кількість його сторін.
а) 15; б) 12; в) 13; г) 14.
9. ( 1 бал) Основи трапеції дорівнюють 9см і 11см, а її площа – 150см2. Знайти висоту трапеції.
а) 7,5см; б) 15см; в) 30см; г) інша відповідь
- (2 бали) Знайти площу паралелограма, висоти якого дорівнюють 16см і 20см, а сторони відрізняються на 2см.
- ( 2 бали) В трикутнику АВС ∠А=75°, ∠В=30°, АВ=10см. Знайти площу трикутника.
12. ( 2 бали) В рівнобедреній трапеції, висота, проведена з вершини тупого кута, ділить більшу основу на відрізки, більший з яких 20см. Знайти площу трапеції, якщо її висота 12см.
Варіант ІІ
1.(0,5 бала) Вибрати невірне твердження.
а) Многокутник опуклий, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону;
б) рівні фігури мають рівні площі;
в) площа кожного многокутника є невід’ємним числом;
г) площа паралелограма дорівнює добутку його сторони на висоту, проведену до цієї сторони.
2.(0,5 бала) Скільки діагоналей в опуклого шестикутника?
а) 4; б) 9; в) 6; г) 8.
3. (0,5 бала) Сума внутрішніх кутів опуклого п’ятикутника
а) 360°; б) 540°; в) 720°; г) 1080°.
4.(0,5 бала) Центр вписаного в многокутник кола лежить на перетині
а) бісектрис;
б) висот;
в) діагоналей;
г) серединних перпендикулярів.
- (0.5 бала) Діагоналі ромба 8см і 4см. Його площа
а) 48см2; б) 16см2; в) 28см2; г) 24см2.
6. (0,5 бала) Яка з формул є формулою для обчислення площі трапеції?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
7. ( 1 бал) У квадрат, площа якого 81см2 вписано коло. Чому дорівнює радіус даного кола?
а) 16см; б) 8см; в) 4,5см; г) 32см.
8.( 1 бал) В опуклому многокутнику сума його внутрішніх кутів дорівнює 1980°. Знайти кількість його сторін.
а) 15; б) 12; в) 13; г) 14.
9. ( 1 бал) Основи трапеції дорівнюють 15см і 11см, а її площа – 182см2. Знайти висоту трапеції.
а) 7,5см; б) 15см; в) 14см; г) інша відповідь
- (2 бали) основи трапеції дорівнюють 7 см і 13 см, а її площа – 40 см2. Знайдіть висоту трапеції.
- ( 2 бали) В трикутнику АВС ∠А=65°, ∠В=30°, АВ=10см. Знайти площу трикутника.
- 12. ( 2 бали) Сторони квадратів 14 см і 16 см. Чому дорівнює сторона квадрата, площа якого дорівнює різниці площ даних квадратів?
Додаткові завдання
№ 1. Середня лінія трапеції дорівнює 23 см, висота – 10 см. Знайти площу трапеції.
№ 2. Площа трикутника 85 м2, а його висота – 17 м. Знайти сторону трикутника, до якої проведена висота.
№ 3. Площа трапеції дорівнює 84 см2, а висота – 8 см. Знайти основи трапеції, якщо одна з них на 5 см більша за другу.
№ 4. Сторони паралелограма дорівнюють 21 см і 12 см, а менша висота 4 см. Знайти більшу висоту.
№5. У паралелограмі бісектриса кута, що дорівнює 30°, ділить його сторону на відрізки 24 см і 16 см, починаючи від вершини тупого кута. Знайти площу паралелограма.
№6. У ромбі діагоналі відносяться як 3:5. Знайти діагоналі ромба, якщо його площа 32 см2.
Тема 8. Систематизація знань. Підготовка до контрольної роботи
Мета:
Навчальна складова:
- Закріпити та узагальнити знання учнів з теми «Многокутники. Площі многокутників»
- вдосконалювати вміння застосовувати теоретичні знання при розв’язуванні задач.
Розвивальна складова:
- розвивати творчі здібності, вміння аналізувати, робити висновки.
Виховна складова:
- Виховувати відповідальність, почуття колективізму.
Методичні рекомендації
Урок можна провести методом розв҆язування доцільних завдань.
Індивідуальні завдання
Учням потрібно заповнити таблицю, у розданих учителем індивідуальних картках.
|
Види чотирикутника
Властивості |
Паралелограм |
Прямокутник |
Ромб |
Квадрат |
|
Протилежні сторони попарно паралельні |
|
|
|
|
|
Всі кути рівні |
|
|
|
|
|
Всі сторони рівні |
|
|
|
|
|
Діагональ поділяє на два рівних трикутники |
|
|
|
|
|
Діагоналі в точці перетину поділяються навпіл |
|
|
|
|
|
Діагоналі рівні |
|
|
|
|
|
Протилежні сторони і кути рівні |
|
|
|
|
Розв҆язування задач за готовими рисунками
Задача 1. За готовим рисунком знайти площу трапеції АВСD. Пояснити, як знайшли висоту АН.
Розв'язання:
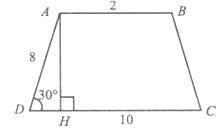
У трикутнику АDН із прямим кутом Н проти кута 30° лежить катет, що дорівнює половині гіпотенузи.
Отже, АН = 4 см.
![]() (см2).
(см2).
Задача 2. За готовим рисунком знайти площу трапеції АВСD. Пояснити, як знайшли висоту і більшу основу трапеції.
Розв’язання:
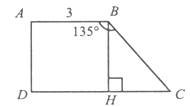
![]() (см2).
(см2).
Задача 3. Кожній зображеній фігурі (додаток 1) поставити у відповідність формулу обчислення площі (додаток 2).
(Список формул надається учневі, якщо у нього виникають проблеми виконати завдання самостійно!)
Додаток 1
Додаток 2
![]()
Розв’зування комбінованої задачі
Розв’зування комбінованої задачі передбачає:
- диференціацію (у роботі беруть участь учні з достатнім та високим рівнями навчальних досягнень);
- нестандартний підхід у поданні матеріалу;
- ігрову ситуацію з елементами пошуку та аналізу.
На дошці малюнок «Корабель». Учні по черзі виходять до дошки, називають фігуру, яку розглядають, називають формулу для знаходження площі цієї фігури, виконують обчислення, записують відповідь.
Задача. Знайти Sфігури. Відомо, що AV=VH, НЕ=EN, BH=CK, SRSQ=SVNH (Рис. 1).
Розв’язання:
1. Чи є всі дані для обчислення площі чотирикутника ABCD?
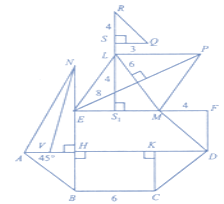
Рис. 1
2. Що це за фігура? (Трапеція ABCD.)
3. Що необхідно знайти для знаходження площі трапеції? (Основи і висоту.)
4. З якої фігури почнемо розв’язувати задачу? (З трикутника SQR.)
![]() (см2).
(см2).
5. Яка наступна фігура? (Ромб ELPM.)
6. Яким чином ви визначили, що це ромб? (Ознака ромба за діагоналями.)
![]() (см2).
(см2).
7. Як знайти ЕМ? (Використаємо другу формулу для обчислення площі ромба через основу і висоту.)
SELPM=LS1∙EM;
24=4EM;
ЕМ=6 см.
8. Яку фігуру розглядатимемо далі? (Прямокутник HEFD.)
9. Як знайти виміри HEFD?
EF=EM+MF=6+4=10 см.
DM – бісектриса кута FDK, ∠FDK=45°, ∠F=90°.
Отже, ∠FMD=45°.
ΔMFD – рівнобедренний з основою MD, FD=FM=4 см.
Тоді ЕН=FD=4 см.
10. Якими будуть ваші подальші міркування? (Можна знайти NH=8 см, розглянути трикутники NVH i NHA.)
За умовою задачі SRSQ=SVNH=6 см2. За теоремою про відношення площ двох трикутників, що мають рівні кути: ![]() см2.
см2.
Звідси можна знайти АН: ![]() ; АН=3 (см).
; АН=3 (см).
11. Чи можна перейти до розгляду трапеції ABCD? (Так.)
AD=AH+HD=3+10=13 см; HD=EF=10 см; ΔAHB – рівнобедренний з основою АВ. АН=ВН= 3 см – висота трапеції ABCD. Тоді
![]() (cм2).
(cм2).
Зауваження: під час розв’язування комбінованої задачі класом з учням із початковим та середнім рівнями навчання запропоновані 6 задач ( кожна на одну формулу). До них додається набір формул, які можна використати під час розв’язування цих задач.
ля узагальнення та систематизації вивченого матеріалу з теми «Многокутники. Площа многокутників» пропоную розгадати кросворд.
КРОСВОРД
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
|
|
|
ш16 |
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
і |
|
п2 |
е |
р |
и |
м1 |
е |
т |
р |
|
|
о |
|
|
|
|
|
|
|
|
ш3 |
е |
с |
т |
и |
к |
у |
т |
н |
и |
к |
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
т |
|
д4 |
і |
а |
г |
о |
н |
а |
л |
ь |
|
у |
|
|
|
|
|
|
п14 |
҆ |
я |
т19 |
ь |
|
|
|
|
|
г |
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
п5 |
р |
о |
т |
и |
л |
е |
ж |
н |
і |
|
|
|
|
|
|
|
|
и |
|
|
|
о6 |
п |
у |
к |
л |
и |
й |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к15 |
у |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
ч7 |
о |
т |
и |
р |
и |
к |
у |
т |
н |
и |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
т9 |
р |
и |
к |
у |
т |
н |
и |
к |
|
|
|
|
|
|
|
|
|
|
|
п10 |
р20 |
я |
м |
о |
к |
у |
т |
н |
и |
к |
|
|
п21 |
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
к11 |
в |
а |
д |
р |
а |
т22 |
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
я |
|
р |
|
|
|
|
|
|
|
|
н13 |
е |
в |
и |
п |
у |
к |
л |
и |
й |
|
|
м |
|
а |
|
|
|
|
|
|
|
р12 |
і |
в |
н14 |
о |
б |
і |
ч23 |
н |
а |
|
|
|
і |
|
п |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
о |
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
т |
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
и |
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
р |
|
|
|
|
|
|
|
я |
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п8 |
а |
р |
а |
л |
е |
л |
о18 |
г |
р |
а |
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
По горизонталі:
1. Одиниця виміру шляху.
2. Сума довжин усіх сторін.
3. Назва многокутника з шістьма вершинами.
4. Відрізок, що з'єднує дві не сусідні вершини многокутника.
5. Дві несуміжні сторони чотирикутника називаються ... . Або дві вершини, які не є сусідніми, називаються ... .
6. Як називається многокутник, якщо він лежить по одну сторону від кожної прямої, що проходить через дві сусідні вершини.
7. Назва многокутника, сума кутів якого дорівнює 360 градусів.
8. Чотирикутник, у якого протилежні сторони попарно паралельні.
9. Сума кутів будь-якого ... дорівнює 180 градусів.
10. Паралелограм, у якого всі кути прямі.
11. Прямокутник, у якого всі сторони рівні.
12. Як називається трапеція, що має рівні сторони?
13. Вид чотирикутника (рис. 2)
рис.2.
- Скільки сторін має многокутник, кожен кут якого дорівнює 108 градусів.
По вертикалі:
1. Фігура, складена з відрізків АВ, ВС, СД, ... , ЕF, FA, так що суміжні відрізки не лежать на одній прямій, а не суміжні відрізки не мають спільних точок.
15. Один з елементів трикутника. Або геометрична фігура, яка складається з двох променів, що мають спільний початок.
16. Скільки сторін має многокутник, кожен кут якого дорівнює 120 градусів.
17. Трапеція, у якої один з кутів прямий.
18. Назва паралельних сторін трапеції.
19. Скільки сторін має многокутник, кожен кут якого дорівнює 60 градусів.
20. Властивість прямокутника: діагоналі прямокутника ... .
21. Властивість квадрата: всі кути квадрата ... .
22. Чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні.
23. Скільки сторін має многокутник, кожен кут якого дорівнює 90 градусів.
Тема 9. Тематична контрольна робота
Мета:
Навчальна складова:
- перевірити навчальні досягнення учнів з теми «Многокутники. Площа многокутників»
Розвивальна складова:
- розвивати зосередженість, розумові здібності, впевненість у своїх силах.
Виховна складова:
- Виховувати зібраність, сумлінність, здатність до переборення труднощів.
КОНТРОЛЬНА РОБОТА
Варіант І
- (0,5 бала)Укажіть малюнок, на якому зображено п҆ятикутник, вписаний у коло.
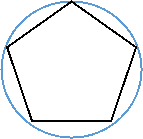
А. Б. В. Г.
2. (0,5 бала)Знайдіть площу прямокутника, сторони якого дорівнюють 6 см і 7 см.
А. 13 см2 Б. 42 см2 В. 26 см2 Г. 21 см2
3.(0,5 бала)Знайдіть площу паралелограма, одна зі сторін якого дорівнює 9 см, а висота проведена до неї – 4 см.
А. 18 см2 Б. 13 см2 В. 36 см2 Г. 26 см2
4.(1 бал) Обчисліть суму кутів опуклого 13-кутника.
5.(1 бал) Площа трикутника дорівнює 45 см2, а одна з його сторін – 18 см. Знайдіть висоту трикутника, проведену до цієї сторони.
6.(1,5 бала)Площа трапеції дорівнює 24 см2, одна з її основ – 5 см, а висота – 4 см. Знайдіть другу основу трапеції.
7.(2 бала) Прямокутник зі сторонами 10 дм і 9,5 дм розрізали на квадрати, сторона кожного з них 0,5 дм. Скільки утворилося квадратів?
8.(2 бала) Знайдіть площу ромба, одна з діагоналей якого дорівнює 24 см, а сторона – 13 см.
9.(3 бала) Більша основа рівнобічної трапеції дорівнює 12 см. Точка перетину діагоналей трапеції віддалена від основ на 6 см і 5 см. Знайдіть площу трапеції.
Варіант ІІ
- (0,5 бала)Укажіть малюнок, на якому зображено шестикутник, описаний навколо кола.
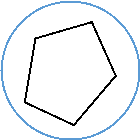
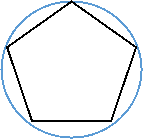
А. Б. В. Г.
2. (0,5 бала)Знайдіть площу прямокутника, сторони якого дорівнюють 4 см і 9 см.
А. 13 см2 Б. 18 см2 В. 26 см2 Г. 36 см2
3.(0,5 бала)Знайдіть площу паралелограма, одна зі сторін якого дорівнює 8 см, а висота проведена до неї – 5 см.
А. 40 см2 Б. 20 см2 В. 13 см2 Г. 26 см2
4.(1 бал) Обчисліть суму кутів опуклого 9-кутника.
5.(1 бал) Площа трикутника дорівнює 30 см2, а одна з його висот – 12 см. Знайдіть довжину сторони, до якої проведена ця висота.
6.(1,5 бала)Площа трапеції дорівнює 24 см2, одна з її основи - 5 см і 11 см. Знайдіть висоту трапеції.
7.(2 бала) Прямокутник зі сторонами 8 дм і 4,8 дм розрізали на квадрати, сторона кожного з них 0,4 дм. Скільки утворилося квадратів?
8.(2 бала) Знайдіть площу ромба, сторона якого дорівнює 17 см, а одна з діагоналей – 30 см.
9.(3 бала) Точка перетину діагоналей рівнобічної трапеції віддалена від основ на 3 см і 5 см. Знайдіть площу трапеції, якщо її більша основа дорівнює 20 см.
Варіант ІІІ
- (0,5 бала)Укажіть малюнок, на якому зображено шестикутник, вписаний у коло.
А. Б. В. Г.
2. (0,5 бала)Знайдіть площу прямокутника, сторони якого дорівнюють 6 см і 8 см.
А. 14 см2 Б. 24 см2 В. 48 см2 Г. 28 см2
3.(0,5 бала)Знайдіть площу паралелограма, одна з висот якого дорівнює 7 см, а сторона, до якої вона проведена – 5 см.
А. 11 см2 Б. 22 см2 В. 28 см2 Г. 14 см2
4.(1 бал) Обчисліть суму кутів опуклого 8-кутника.
5.(1 бал) Одна зі сторін трикутника дорівнює 8 см. Знайдіть висоту трикутника, проведену до неї, якщо площа трикутника дорівнює 12 см2.
6.(1,5 бала)Площа трапеції дорівнює 36 см2, а висота трапеції – 6 см. Знайдіть основу трапеції, якщо друга її основа дорівнює 7 см.
7.(2 бала) Прямокутник зі сторонами 4 дм і 3,6 дм розрізали на квадрати, сторона кожного з них 0,2 дм. Скільки утворилося квадратів?
8.(2 бала) Сторона ромба дорівнює 10 см, а одна з діагоналей – 16 см. Знайдіть площу ромба.
9.(3 бала) Менша основа рівнобічної трапеції дорівнює 8 см. Точка перетину діагоналей трапеції віддалена від основ на 2 см і 3 см. Знайдіть площу трапеції.
Варіант ІV
- (0,5 бала)Укажіть малюнок, на якому зображено п҆ятикутник, вписаний у коло.
А. Б. В. Г.
2. (0,5 бала)Знайдіть площу прямокутника, сторони якого дорівнюють 6 см і 5 см.
А. 30 см2 Б. 15 см2 В. 11 см2 Г. 22 см2
3.(0,5 бала)Знайдіть площу паралелограма, одна з висот якого дорівнює 8 см, а сторона, до якої проведена ця висота –10 см.
А. 18 см2 Б. 13 см2 В. 36 см2 Г. 26 см2
4.(1 бал) Обчисліть суму кутів опуклого 11-кутника.
5.(1 бал) Площа трикутника дорівнює 26 см2. Знайдіть сторону трикутника, якщо висота, проведена до неї, дорівнює 4 см.
6.(1,5 бала)Основи трапеції дорівнюють 9 см і 3 см. Знайдіть висоту трапеції, якщо її площа дорівнює 30 см2.
7.(2 бала) Прямокутник зі сторонами 9 дм і 7,5 дм розрізали на квадрати, сторона кожного з них 0,5 дм. Скільки утворилося квадратів?
8.(2 бала) Одна з діагоналей ромба дорівнює 40 см, а сторона – 25 см. Знайдіть площу ромба.
9.(3 бала) Точка перетину діагоналей рівнобічної трапеції віддалена від основ на 4 см і 7 см. Знайдіть площу трапеції., якщо її менша основа дорівнює 8 см.
МНОГОКУТНИКИ НАВКОЛО НАС
Математика володіє не тільки істиною, але й вищою, відточеною, суворою, піднесеною чистою красою і прагне до справжньої досконалості, що притаманна найбільшим зразкам мистецтва.
Бертран Рассел










ВИСНОВОК
Дослідження даної теми дало підстави зробити висновок, що у процесі вивчення многокутників розвивається:
- просторове мислення (вид розумової діяльності, що забезпечує створення просторових образів i оперування ними в процесi розв’язання рiзних теоретичних i практичних задач),
- логічне мислення (здатність мислити точно й послідовно, не допускаючи протиріч в своїх міркуваннях, та вміння викривати логічні помилки),
- формування вмінь проводити класифікацію понять, вказуючи структурні зв’язки між ними;
- вміння використовувати вивчений навчальний матеріал для розв'язування різних задач, зокрема практичних.
У даному посібнику запропоновано нестандартні ситуації, роботу в групах та малих групах, цікаві та історичні задачі, задачі на дослідження та підвищеного рівня складності, кросворди, математичні диктанти та тестові завдання, для контролю навчальних досягнень призначена добірка рівневих самостійних робіт та тематична контрольна робота.
Поданий матеріал є досить великим за обсягом і не завжди може бути використаний повністю за відведений час. Учитель на свій розсуд може вибрати те, що найбільше відповідає навчальним можливостям класу, що вважає корисним і необхідним. Матеріал посібника можна використовувати під час вивчення теми «Многокутники. Площі многокутників», це допоможе зробити уроки математики ще більш результативними та цікавими як досвідченому, так і молодому вчителеві.
Структура посібника й зміст завдань дозволяють використовувати його під час роботи за будь-яким чинним підручником з геометрії.
СПИСОК ЛІТЕРАТУРИ
- Навч. програма для загальноосвіт. навч. закл. для 5-9 кл.: Математика. Затверджена Наказом Міністерства освіти і науки України від 07. 06. 2017 р. №804.
- Істер О. С. Геометрія: підр. для 8 кл. загальноосвіт. навч. закл. / О. С. Істер. – Київ: Генеза, 2016.
- Істер О. С. Геометрія: зошит для самост. та темат. контрол. робіт: 8-й кл. / О. С. Істер. – Київ: Генеза, 2016.
- http://oipopp.ed-sp.net/taxonomy/term/637
- http://svyatodumok.blogspot.com/2012/10/blog-post_18.html
- https://ru.osvita.ua/school/lessons_summary/edu_technology/24922/
- http://wotthismaphimaphix.blogspot.com/
1
-
Дякую!


про публікацію авторської розробки
Додати розробку