Міні-підручник "Вписані і описані чотирикутники"

Гімназія № 107 «Введенська» Кафедра математики     Тренувально-узагальнюючий збірник завдань з геометрії _________________________________ _________________________________                 Київ – 2020

 оцінно-смисловий етап

 «Де тонко – там і рветься»

 (Народна мудрість)

Мета: з’ясувати «де тонко»

Коло, описане навколо чотирикутника

 Коло називається описаним навколо

 чотирикутника, якщо всі його вершини лежать на

 цьому колі.

Властивості вершин чотирикутника, вписаного в коло:

1. Усі вершини чотирикутника, вписаного в коло, є рівновіддаленими від центра кола.
2. Відстань від центра описаного кола до будь-якої вершини чотирикутника є радіусом цього кола.

 

Коло, вписане в чотирикутник

 Коло називається вписаним в  чотирикутник, якщо

 воно дотикається до всіх сторін чотирикутника.

 

Властивості сторін чотирикутника, описаного навколо кола:

1. Усі сторони описаного чотирикутника є дотичними до кола.
2. Перпендикуляр, опущений із центра вписаного кола до сторони чотирикутника, є радіусом вписаного в цей чотирикутник кола.

 

 системно-узагальнюючий етап

Завдання (виконується у зошиті)

Задача 1

Доведіть, що якщо в трапецію можна вписати коло, то кут, утворений бісектрисами кутів, прилеглих до бічної сторони, прямий.

Задача 2

Доведіть, що в паралелограм можна вписати коло тоді і тільки тоді, коли він є ромбом. Визначте розміщення центра цього кола.

Задача 3

Доведіть, що радіус вписаного в ромб кола у два рази менший за його висоту.

 

 

 

 

 

Наслідки:

1. Якщо в трапецію можна вписати коло, то кут, утворений бісектрисами кутів, прилеглих до бічної сторони трапеції, - прямий.

2. У ромб і квадрат можна вписати коло. Його центр є точкою перетину діагоналей.

3. Радіус вписаного в ромб кола у два рази менший за його висоту.

 

 адаптивно-перетворювальний  етап

Твердження:

Якщо в чотирикутнику суми протилежних сторін рівні, то в нього можна вписати коло. (Для того, щоб довести це твердження, потрібно пригадати властивість бісектриси кута рівнобедреного трикутника, проведеної до її основи).

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

Обернене твердження:

Сума протилежних сторін чотирикутника, у який вписане коло, рівні. (Для того, щоб довести це твердження, потрібно пригадати властивість дотичних, проведених з однієї точки до кола).

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

 оцінно-смисловий етап

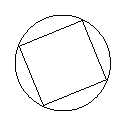
1. Серед запропонованих фігур вибери чотирикутник вписаний в коло:

а)  в) 

 б)

 г)

 

 

2. З’ясуй як правильно закінчити речення

Усі вершини вписаного в коло чотирикутника розташовані на _________________________________________ .

3. Опиши кола навколо довільного паралелограма, ромба, прямокутника

 

 

 

 

 

 

 

Висновок:

______________________________________________________________

______________________________________________________________

 оцінно-смисловий етап

4. З’ясуй як правильно закінчити речення

а) Сторони чотирикутника, описаного навколо кола, є _______________

______________________________________________________________

б) Центр кола, описаного навколо чотирикутника, є точкою перетину ___________________________________

в) Коло не можна вписати в чотирикутник, якщо ___________________

______________________________________________________________

г) Центр кола, вписаного в чотирикутник, є точкою перетину ____________________________________

д) У паралелограм можна вписати коло за умови, що цей паралелограм є ___________________________________

 

5. Серед запропонованих фігур вибери чотирикутник описаний навколо кола. Відповідь обґрунтуй.

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

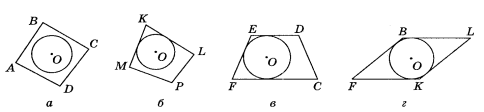
 адаптивно-перетворювальний  етап

6. Впиши коло у довільний паралелограм, ромб, прямокутник, квадрат.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок:

______________________________________________________________

______________________________________________________________

______________________________________________________________

Цікаво знати!

Де зустрічаються вписані і описані чотирикутники в навколишньому світі?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Завдання: Поглянь навкруг себе і спробуй відшукати в оточуючому світі аналогічні фігури. Сфотографуй і поділися враженнями.

 

Тренувально-узагальнюючий збірник завдань розроблено на кафедрі природничо-математичних дисциплін.

Автор Бережна Юлія Миколаївна – вчитель математики.