Многочлен. Подібні члени многочленна та їх зведення

Тема. Многочлен. Подібні члени многочленна та їх зведення

Мета: домогтися свідомого сприйняття учнями змісту понять «много­член», «подібні члени многочлена», «многочлен стандартного вигляду», «степінь многочлена» та вдосконалити вміння зводити подібні доданки (подібні члени многочлена).

Тип уроку: засвоєння знань, формування вмінь.

Хід уроку

І. Організаційний етап. Аналіз тематичної контрольної роботи

 Оскільки за браком часу приділити цілий урок аналізу помилок, допущених під час виконання тематичної контрольної роботи, неможливо, це питання розв'язуємо індивідуально, тобто під час перевірки тематичної контрольної роботи аналізуємо роботи учнів за планом:

1. тема, яку учень не засвоїв на належному рівні;
2. питання, які треба повторити.

Після оголошення оцінок роздати учням рекомендації (до речі, вико­нана учнями вдома після тематичної контрольної роботи (див. попередній урок) «рефлексія» може бути оцінена і врахована як корекція знань учнів). Подальша робота організовується за бажанням вчителя: або це буде індивідуальний залік (можна залучити учнів-консультантів), або робота з корекції знань, або, можливо, яка-небудь інтерактивна гра (у позаурочний час).

II. Робота з випереджальним домашнім завданням

 Якщо вдома учні успішно попрацювали із текстом підручника (тема «Многочлени» за планом), то робота, яку треба здійснити в класі, полягає в корекції виконаних учнями завдань.

III. Засвоєння знань

 Попередній етап уроку поступово переходить у етап формування знань, бо серед незрозумілих на початку роботи із текстом підручника термінів учням залишається виділити «нові поняття» і систематизува­ти їх (встановити логіку). Дістанемо зміст нового матеріалу, який треба опрацювати на цьому уроці, зокрема складаємо план:

1. Поняття про многочлен.
2. Поняття про члени многочлена та їм подібні.
3. Многочлен стандартного вигляду.
4. Степінь многочлена стандартного вигляду.

1) Досить складним є питання про правильне означення членів много­члена, тобто часто-густо учні під членами многочленів розуміють модулі цих виразів, тобто знаки членів многочлена сприймають як знак арифметичної дії. Тому під час формулювання означення многочлена акцентуємо увагу учнів на тому, що многочлен — це «алгебраїчна сума», тобто сума, записана в більш короткому вигляді, про який докладно го­ворилося у 6 класі.

2) Обговорюючи зміст поняття «подібні члени многочлена», слід зверну­ти увагу на той момент, що для порівняння членів многочлена на предмет виявлення подібності, слід записати їх у відповідному вигляді, а саме: буквені множники в алфавітному порядку, а числовий множник — на 1-му місці, і показати, що саме з необхідності спростити процес порівняння, «стандартизувати його», випливає необхідність виконання дії, яку ми називаємо «зведення многочлена до стандартного вигляду».

Оскільки тотожні перетворення цілих виразів зводяться до перетво­рення многочлена в многочлен стандартного вигляду, учні добре повинні засвоїти алгоритм перетворення многочлена в многочлен стандартного вигляду, а саме:

1) кожний член многочлена (одночлен) звести до стандартного вигляду;

2) виконати зведення подібних членів многочлена, якщо такі є.

Важливо, щоб учні усвідомили, що названі перетворення були вивчені на попередніх уроках (тема «Одночлени» у 7 класі та тема «Перетворення виразів» 6-7 класи), тобто на уроці ми активізуємо відповідні знання й уміння, залучивши більш широкий термінологічний апарат.

Оскільки теоретичні відомості виписані й відпрацьовані учнями на початку уроку, окремо записувати конспект на уроці не має сенсу. Бажано більше навчального часу приділити саме розв'язуванню вправ.

IV. Застосування знань, засвоєння вмінь

 Система завдань, запропонованих для розв'язування на цьому уроці, складається з двох основних блоків: 1) завдання на закріплен­ня термінології; 2) завдання на формування навичок застосовувати алгоритм зведення многочлена до стандартного вигляду (закріп­люємо знання відповідного алгоритму та вдосконалюємо навички перетворення одночлена в одночлен стандартного вигляду та на­вички зведення подібних доданків, тобто застосування розподіль­ної властивості множення відносно додавання).

Виконання усних вправ

1. Які з наведених виразів є многочленами? Чому?

1) 3а³ + bc² – ab;  2) 3х + 5; 3) а; 4) а² + а; 5) т(2п – k); 6) (х - 3у)³;

7) ;  8) -2k; 9) 4,5.

 Бажано, щоб під час виконання цього завдання учні повторили, як читаються вирази (тобто спочатку прочитати), а також види виразів (класифікація на цілі та дробові вирази).

2. Чи є подібні члени в таких многочленах:

1) 4а – 3 – а + 1,5;   2) 4ху + 4х + 4у;

3) 3п² + 4п – 2п² + п – 1;   4) а² + ab + b² + ba?

3. Назвіть многочлени стандартного вигляду та знайдіть їхні степені:

1) с² + 4с – 2; 2) х + у +1; 3) х;  4) 6а – а² + 5а + 2; 5) 4у – у ∙ 2у; 6) bс+3.

4. Які дії треба виконати, щоб записати даний многочлен у стандартному вигляді: 1) 4а + 3 + а – 2;  2) 2aba + 3; 3) х + у + 2х – у?

Виконання письмових вправ

1. Зведіть подібні члени многочлена:
   1) 4a²b – 3ab² – a²b + 2ab²; 2) x² + 4х – 5 – 3х + 2;

3) 10a – 6b + 5c – 4d + 9a – 2b – 8c – 2d;

4) 2а⁴ – 8а³b – 2а²b² – 4ab³ – 3а⁴ + 8а³b + 9а²b² + ab³.

2. Зведіть многочлен до стандартного вигляду та вкажіть його степінь:
   1) 3a²ab – 4a²b²b² – 6ab ∙ 2a + 5a³b ∙ 0,4ab³;

2) 12x² ∙ 3ху – 2ху ∙ 3у³х + 12хух;

3) .

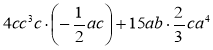3. Зведіть многочлен до стандартного вигляду та знайдіть його значення
   при вказаних значеннях змінних:

1) -4а³ + 10а² + 8а³ – 12а² + 5а, якщо а = -2;

2) 3а²b – аb² + 2а²b – 6аb² + 9аb², якщо а = 0,2; b = -5;

3) -4а²b³ +7аb³ – аb³а + b²аb – 8аb³, якщо а = - 0,5; b = 2.

4*. Запишіть у вигляді многочлена (і в позиційному запису) число, яке має: 1) а сотень, b десятків, с одиниць; 2) т тисяч, п сотень, k одиниць;

3) а тисяч, b десятків, с одиниць.

5. Повторення. Розкрийте дужки і зведіть подібні доданки.

1) 4а – 3 + (3а + 5 – 2а); 2) (-3а + 4b) – (2а – 1) + 6b;

3) (-4х + 4) – (3х – у) – (2 + 2у).

V. Підсумки уроку. Рефлексія

Наведіть приклади та контрприклади (якщо це можливо) до названих понять: 1) многочлен; 2) члени многочлена; 3) подібні члени многочлена; 4) многочлен стандартного вигляду; 5) степінь многочлена стандартного вигляду.

VI. Домашнє завдання

№ 1. Зведіть многочлен до стандартного вигляду:

1) 7т³тр² – 6тр²р⁴ + 11т²п ∙ 3п – 0,2тп³ ∙ 5т³п;

2) 16aa²a ∙ a²b + 12ab ∙ a²b³;

3) 2a³b – 5ab³ – 7a³b + ab³;

4) 7a⁴ + 12a³b + 3a²b² – 7ab³ + 5a⁴ – 9a³b – 3a²b² – ab⁵.

№ 2. Зведіть многочлен до стандартного вигляду та знайдіть його зна­чення при вказаних значеннях змінної х:

1) 0,4b³ - 0,2b² + 0,5b - 0,3b³ – 0,5b + 7, якщо b = -2;

2) -4а² b + 3аb² + 3а²b – 5аb² + 5а²b, якщо а = 5, b = -0,4.

№ 3. Випереджальне домашнє завдання. Запишіть у вигляді виразу:

1) суму двох виразів: суми х і у та їх різниці:

2) різницю двох виразів: суми х і у та їх різниці.

Які, користуючись текстом підручника та (або) конспектом, перетво­рення виразів і в якому порядку треба виконати, щоб спростити ці вирази?