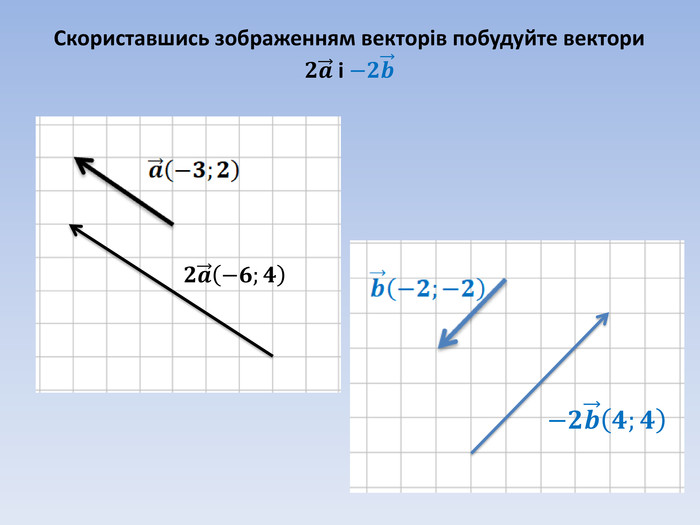
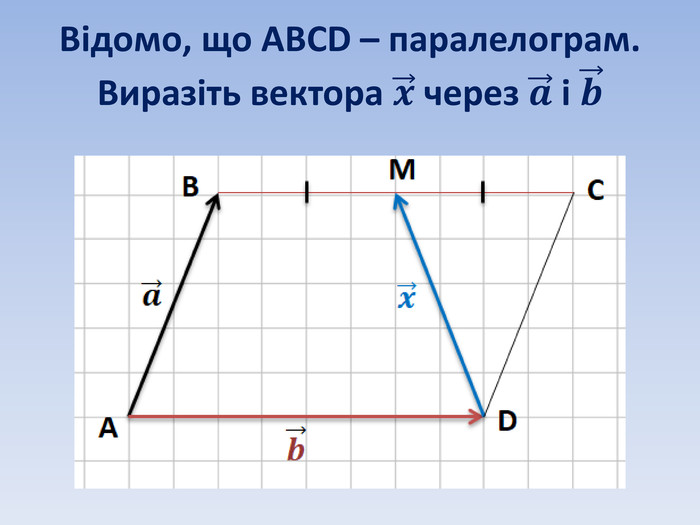
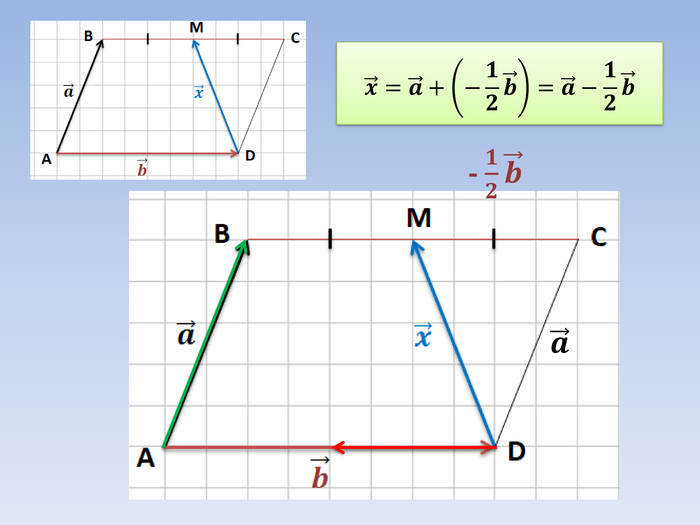
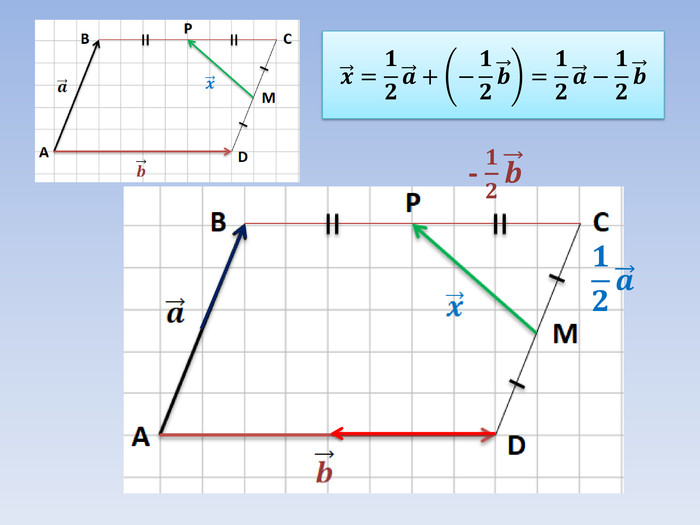
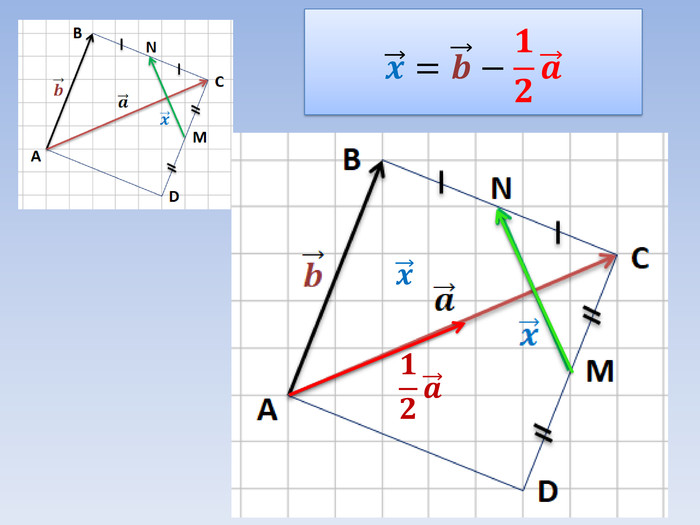
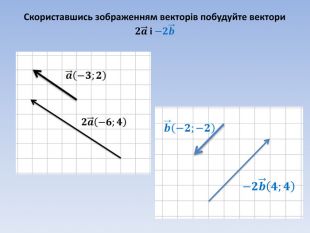
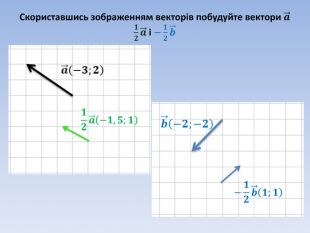
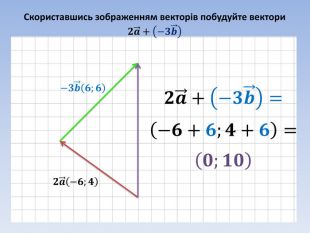
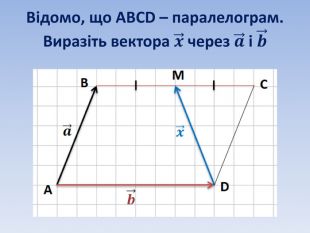
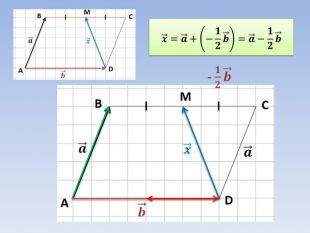
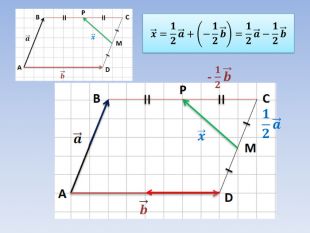
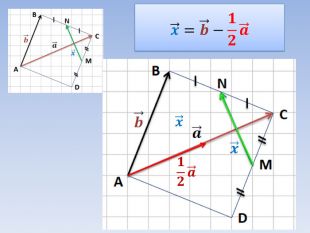
Вектори. Дії з векторами. Підготовка до самостійної роботи
Про матеріал
Матеріал може бути використаний як до уроку з теми так і до уроку при дистанційному навчанні Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку