Департамент освіти і науки України

Дніпропетровської обласної державної адміністрації

Управління освіти і науки виконкому Криворізької міської ради

Відділ освіти виконкому Покровської районної у місті ради

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підготували:

Вчитель математики,

КЗШ І-ІІІ ступенів №97

Люта Ганна Петрівна.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

м. Кривий Ріг - 2021

Тема уроку: Підмножина. Операції над множинами.

Формування компетентностей:

• предметна компетентність:
• сформувати поняття операції над множинами, а саме: дати означення підмножини, перерізу, об’єднання, різниці й доповнення множини;
• навчати учнів здійснювати операції над множинами;
• вміти застосовувати означення операції над множини при розв’язування вправ, при розв’язуванні рівнянь, систем рівнянь, нерівностей;
• уміння вчитися впродовж життя;
• розвивати логічне і абстрактне мислення;
• розвивати знання учнів про множину та її елемен­ти, порожню множину, способи задання множин та про операції над множинами: об'єднання, переріз, різниця множин.
• спілкування державною мовою;
• виховувати культуру математичного запису та мови.

 

Тип уроку: засвоєння нових знань.

Обладнання та наочність: презентація, множини, операції над множинами

Хід уроку

1. Організаційний момент
2. Актуалізація опорних знань

    

     І. «Дерево знань»

 

1. Навести приклади множин;
2. Як позначають множину та її елементи?
3. Які числа називаються натуральними, цілими?
4. Дати означення раціональних та ірраціональних чисел;
5. Ознаки подільності на 2, 5, 10, 3, 9;
6. Які множини називаються рівними?
7. Способи завдання множин;
8. Яку множину називають порожньою? Як її позначають?

  

 

 

 

     ІІ. «Заморочки із бочки» (самостійна робота, робота в парах)

  1. Дано функцію f(x) = x²+1. Поставте замість зірочки знак або так, щоб отримати правильне твердження:

 1) 3 * D(f);   3) 0 * E(f);  5) 1,01 *E(f).

 2) 0 * D(f);   4) ½ * E(f); 

  Розв’язки:

 1. f(3) = 3² + 1 = 10; 3 D(f).    5. 1,01 = x² + 1; x = 0,1;  1,01 E(f) 

 2. f(0) = 1; 0 D(f).    4. ½ = х² + 1; х² = -½; ½ Е(f).

 3. 0 = x² + 1; x² = -1; 0 Е(f).  

  2. Запишіть множину коренів рівняння:

 1) х(х – 1) = 0;   3) х = 2;

 2) (х – 2)(х² – 4) = 0;  4) х² + 3 = 0. 

 Розв’язки:

 1. х(х – 1) = 0; х = 0 або  х =1; В: {0;1}.

 2. х – 2 = 0 або (х – 2)(х + 2) =0; В: {-2;2}.

 3. В: {2}.

 4. х² = – 3. В: Ø .

 3. Записати множини, перелічивши їхні елементи:

  Додатні числа, кратні числу 7 і менші від 60.

 В: {7,14,21,28,35,42,49,56}.

3. Повідомлення теми і мети уроку

Сьогодні ми маємо познайомитися з поняттям підмножини, її елементами, навчитися виконувати операції над ними

4. Вивчення нового матеріалу.

Якщо кожен елемент однієї множини A є елементом множини B, то кажуть, що перша множина A є підмножиною  множини B. Це записують так: A ⊂ B.

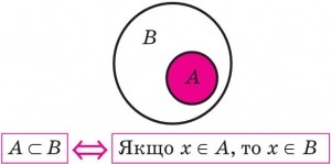Наприклад, {1; 2} ⊂ {0; 1; 2; 3}, N ⊂ Z  (оскільки будь-яке натуральне число — ціле), Z ⊂ Q  (оскільки будь-яке ціле число — раціональне),  Q  ⊂  R  (оскільки будь-яке раціональне число — дійсне).

Вважають, що завжди ∅ ⊂ A, тобто порожня множина є підмножиною будь-якої не порожньої множини.

Інколи замість запису A ⊂ B використовують також запис A ⊆ B, якщо множина A або є підмножиною множини B, або дорівнює множині B. Наприклад, A ⊆ A.

Співставимо означення рівності множин з означенням підмножини.

Якщо множини А і В рівні, то:

1. кожний елемент множини А є елементом множини B, отже,

А — підмножина В

(A ⊆ B);

2. кожний елемент множини В є елементом множини А, отже,

В — підмножина А

(B ⊆ A).

Таким чином, дві множини рівні, якщо кожна з них є підмножиною іншої. Інколи співвідношення між множинами зручно ілюструвати за допомогою кругів (які часто називають кругами Ейлера-Венна).

Наприклад:

Записати всі підмножини М = {5;12;6}.

М = {5;12;6}.

Ø ⊂ М, {5}⊂М, {12}⊂М, {6}⊂М,

{5,12}⊂М, {5,6}⊂М, {12,6}⊂М, М⊆М.

Операція перетину множин

Перетином множин А і В називають їхню спільну частину, тобто множину C усіх елементів, що належать як  ,  так і множині В. Перетин множин позначають знаком  ∩ (на рисунку наведено ілюстрацію означення перетину множин).

Наприклад, якщо A = {2; 3; 4}, B = {0; 2; 4; 6}, то A ∩ B = {2; 4}.

Нехай А множина розв’язків рівняння х + у = 5, а В – множина розв’язків рівняння х – у = 3. Тоді множина С розв’язків системи рівнянь

            

 

    2х = 8; х = 4; у = 1. В: {(4;1)}.

 Можна записати С = А∩В = {(х;у)|х + у = 5)∩{(х,у)|х – у =3} = {(4;1)}.

 

Операція об’єднання множин

Об’єднанням множин А і В називають множину С, що складається з усіх елементів, які належать хоча б одній із цих множин (А або В). Об’єднання множин позначають знаком ∪ (на рисунку  наведено ілюстрацію означення об’єднання множин).

Наприклад, для множин A і B з попереднього прикладу A∪B = {0; 2; 3; 4; 6}.

Якщо позначити множину ірраціональних чисел через M, то M∪Q = R.

Наприклад, щоб розв’язати систему рівнянь треба знайти перетин трьох множин

х = 5 – у; х = 3 + у; 5 – у = 3 + у, у = 1, х² = 16, х = ±4.

В: А∪В∪С = {(х,у)|х + у = 5},{(х,у)|х – у =3} i {(x,y)|x² + y² = 17} = {(-4;1;4)}

Об’єднання множин А, В, С – це множина всіх елементів, які належать хоча б одній з цих множин: або множині А, або множині В, або множині С.

 

Об’єднання множин зручно ілюструвати за допомогою діаграм Ейлера.

 

 

 

 

 

Операція різниці множин

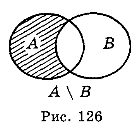
Різницею множин А і В  називається множина С, яка складається з  усіх елементів, які належать множині А  і не належать множині В.

Різницю множин позначають знаком \ (на рисунку наведено ілюстрацію означення різниці множин).

Розглянемо приклади.

а) Якщо А = {a, b, c, d}, В = {а, с, m, n, p}, то А\В = {b, d}, В\А = {m, п, р}.

б) Якщо А — множина учнів вашого класу, В — множина дівча­ток вашого класу, С — множина хлопчиків вашого класу, то А\В = С, А\С = В. У випадку, якщо В — частина множини А (В А), то А\B називається доповненням до В у множині А і позначають С_AВ.

в) Знайти   різницю множин  К={1,2,3,4,5,6,7} і L={2,4,6}:

К = {1,2,3,4,5,6,7};

L = {2,4,6};

K\L = {1,3,5,7}.

Доповнення множини

Якщо B — підмножина A, то різницю A \ B називають доповненням множини B до множини A (рис. 1).

Наприклад, якщо знову позначити множину ірраціональних чисел через M, то
R \ Q = M: кажуть, що множина M ірраціональних чисел доповненням множини A називається множина, яка складається з усіх елементів, які не належать множині А,але які належать універсальній множині U.

Доповнення множини А позначають  Ā  (читають: «А з рискою» або «доповнення А»).

Наприклад, якщо U = R і A = [0; 1], то  Ā = (−∞; 0) ∪  (0; +∞) (Для цього прикладу зручно використати традиційну ілюстрацію множини дійсних чисел на числовій прямій — рис. 3).

 

Сприймання і усвідомлення матеріалу про операції над множинами.

1. Нехай А – множина коренів рівняння х² – 5х + 6 = 0. Які із поданих записів вірні?

а) -5 А;    б) 6 А;     в) 2 А;      г) 3 А .

2. Задайте переліченням елементів множини:

а) А — множину голосних букв українського алфавіту; (А-Я)

б) В — множину коренів рівняння x⁴ - 4х² = 0; (0; 2)

в) С — множину простих парних чисел; (2Z = {…, −6, −4, −2, 0, 2, 4, 6, …})

г) D — множину пір року. (Весна, літо, осінь, зима)

3. Задайте кілька елементів кожної множини:

а) А = {х : х = 2т, де m — ціле число};

б) В = {x : x = 2n + 1, де n — ціле число};

в) С = {х : О < х < 1}.

3. Задано множини:

а) А — множина учнів вашого класу;

б) В — множина учнів вашої школи;

в) С — множина учнів України;

г) D — множина учнів країн земної кулі. Випишіть букви, що позначають вказані множини, в такому порядку, що кожна наступна буква позначала підмножину попередньої множини.

4. Задано множини:

а) множина А всіх трапецій;

б) множина В всіх прямокутників;

в) множина С всіх чотирикутників;

г) множина D всіх квадратів;

д) множина Η всіх паралелограмів;

є) множина F всіх багатокутників.

Запишіть за допомогою знаку с ці множини в такому поряд­ку, що кожна наступна множина була б підмножиною попе­редньої.

5. Зобразіть за допомогою діаграми Ейлера: якщо А В і В С, то А С.

 

Виконання вправ на переріз множин

1. Дано: А = {а, b, с, 1, 3}, В = {b, d, б, 3}, С = {b, 1, 6}. Знайдіть:

а) АB;(b,3)      б) АС; (b,1,)     в) ВС; (b)      г) АВС. (b)

2. Дано: А = {х: х² – 5x + 6 = 0}, B = {x: x² – 3х + 2 = 0}.

Знайдіть: А B. (2)

3. Доведіть: (АB)С = А(BС) = АВС.

4. Доведіть, якщо В А, то А В = В.

5. Доведіть: а) А А = А;   б) А = ;   в) АB = ВА.

 

Виконання вправ на об єднання множин

1. Дано: А = {1, 3, 5, 7}, B = {1, 5, 7, 9}, C = {2, 4}. Знайдіть:

а) АUВ; (1, 3, 5, 7, 9)     6) AUC; (1, 2, 3, 4, 5, 7)      в) BUC; (1, 2, 4, 5, 7, 9)   

г) AUBUC. (1, 2, 3, 4, 5, 7, 9)

2. Дано: А = {x: x² – 5x + 6 = 0}, В = {x: x² – 3х + 2 = 0}. Знайдіть А U В. (1, 2, 3)

3. Доведіть:

а) АUА = А;  б) АU = А;  в) АUВ = ВUА;   г) (АUВ)UС = АU(ВUС).

4. Доведіть: якщо B А, то AUB = А.

 

Виконання вправ на різницю множин

1. Дано: Μ == {a, b, с, d}, N = {b, d}. Знайдіть:

a) M\N; (a, b, c)     б) N\M; (0)       в) (Μ \ Ν) U (Ν \ Μ). (a,b,c)

2. Доведіть:  а) А \ А = ;        б) А \ = А.

V. Підведення підсумків уроку.

1. Що таке множина? (Сукупність будь-яких предметів, об'єктів, об'єднаних між собою деякою загальною для них усіх ознакою)

2. Що таке об’єднання множин? (Об'єднанням множин А і В називається множи­на, яка складається з усіх елементів, які містять­ся хоч в одній з двох множин А, В і тільки їх)

3. Що таке переріз множин? (Перерізом множин А і В називається множина, яка містить усі спільні елементи множин А і В, і тільки їх)

4. Що таке різниця множин? (Різницею множин А і В називається множина всіх таких елементів множини А, які не містять­ся у множині В)

5. Вкажіть серед вказаних нижче множин порожню:

а) множина коренів рівняння х² - 4 = 0;

б) множина коренів рівняння х = х + 2;*

в) множина коренів рівняння х + 1 = 1 + x;

г) множина кіл, в яких діаметр менший від радіуса.

6. Доведіть, що, якщо А В, а В С, то А С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

VI. Домашнє завдання.

А.Г. Мерзляк, В.Б. Полонський, Алгебра 8 клас, Підручник для класів з поглибленим вивченням математики.

п. 5, стор. 28, №№ 5.30, 5.23.

Для самостійного опрацювання: М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук, Алгебра і початки аналізу, 10-11 клас. Розділ 12, сторінка 455, Рівень А, №№ 1-4, Рівень Б, №№ 5-8, Рівень В, №№ 9-12.

 

 

Використана література

1. Мерзляк А.Г. Алгебра: Підручник для 8 класів з поглибленим вивченням математики/ Мерзляк А.Г., Полонський В.Б, Якір М.С. - Х.: Гімназія, 2008. – 368 с.

2. Шкіль М.І. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів/ М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчик. – 2-ге вид. – Зодіак-ЕК, 2001. – 656 с.

3. Алгебра і початки аналізу в таблицях. 7-11 клас. Навчальний посібник. Науково методичний центр, 2003. – 248 с.

4. Алгебра в таблицах (с приложеним). Учебное пособие для учащихся 7-11 классов. – Н49 Х.: Мир детства, 1998. – 116 с. Приложение 56 с.

5. Об`єднання вчителів математики [Електронний ресурс]/ http://matematik.org.ua/