Модуль числа та його застосування

Про матеріал

Важливим завданням вчителя є виявлення і розвиток здібностей і навчальних можливостей кожного учня. Цього можна досягти впровадженням різних форм навчання. Однією з таких форм є нетрадиційні уроки, які активізують діяльність учнів, зацікавлюють їх, розвивають здібності і нахили, самостійність у діях і мисленні, сприяють розвитку творчості, виявленню індивідуальних особливостей. Саме тому я пропоную один із таких уроків, який може бути використаний для роботи з учнями у 6 класі.

Перегляд файлу

Тема. Модуль числа.

Мета: навчальна: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв'язування рівнянь.

Розвиваюча: розвивати пізнавальний інтерес, потребу в самоосвіті.

Виховна: виховувати розуміння ролі математики в житті, розуміння важливості математичних знань.

Тип уроку: застосування знань, умінь і навичок

Обладнання: комп’ютер, презентація, підручник

Хід уроку

І. Організаційний етап.

Організація уваги учнів.

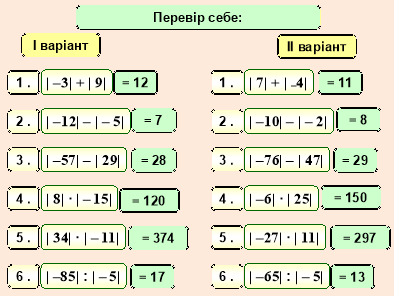
ІІ. Перевірка домашнього завдання.

Домашнє завдання перевірити, викликавши кількох учнів до дошки (заздалегідь).Потім взаємоперевірка за зразком.

ІІІ. Формування мети і завдань уроку

Основна мета уроку — сформувати вміння учнів розв'язувати рівняння, використовуючи означення модуля.

IV. Мотивація навчальної діяльності

Історична довідка:

V. Актуалізація опорних знань

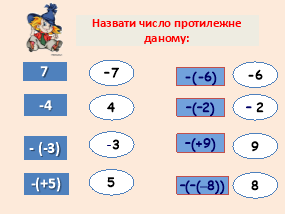
VI. Актуалізація опорних знань

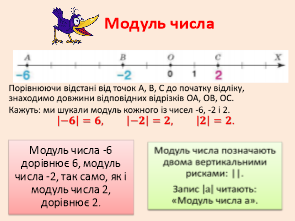
Математичний диктант

Запишіть рівність: модуль числа -5 дорівнює 5. Чи правильна ця рівність?
Чому дорівнює модуль числа ?
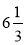Чому дорівнює модуль числа 0 ?
Чому дорівнює модуль числа -3 ?
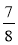Модуль числа х дорівнює 4,1. Чому дорівнює модуль числа, протилежного до х?

VII. Поглиблення знань

Розв’язання рівнянь : слайд 14, 15, 16

Робота із підручником № 1011

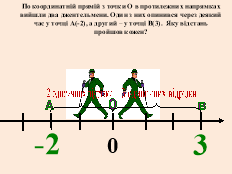
Відстань між двома точками на координатній прямій

а)

Нехай дано А(а) і B(b) і нехай b > а додатні; тоді

АВ = ОВ - ОА = b – а = |b| - |а|.

Наприклад, якщо A(5,3); В,то

АВ = 7 – 5,3 = 7,25 – 5,30 = 1,95 (од. відр.)

б)

Нехай дано А(а) і B(b), причому а – від'ємне, b – додатне. Тоді

АВ = AO + OB = |a| + |b|.

Наприклад, якщо А (-5,3), В , то АВ = |-5,3| + = 5,3 + 7,25 = 12,25 (од. відр.)

в)

Нехай дано А(а) і B(b), причому а і b — від'ємні, тоді якщо а ближче до О (|a| < |b|), то AB = |a| - |b|.

Якщо ж а далі від 0, ніж b, то AB = |b| - |а|.

Наприклад, A(-5,3), В, тоді оскільки |-5,3| < , то

АВ= - |-5,3| = 7 - 5,3 = 1,95 (од. відр.).

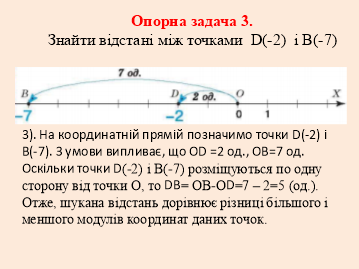
Висновок

знаходження відстані між двома точками на координатній прямій.

IV. Відпрацювання навичок№ 1011, 1016

VІІІ. Підсумки уроку.

Дидактична гра «Опиши число»

На дошці записано ціле від'ємне число, наприклад 9. Учні (або 1 учень-експерт) повинні швидко відповісти на запитання, які вчитель ставить у короткій формі:

1) Яке це число?

2) Його модуль?

3) Йому протилежне?

4) Йому обернене?

5) Де розташовано на координатній прямій?

6) Відстань від початку відліку?

7) Відстань між ним і йому протилежним?

8) Число, що має менший модуль.

ІХ. Домашнє завдання

1015, 1016, 1026