Розв'язування вправ на тему «Співвідношення між сторонами і кутами трикутника»

УРОК № 3

Тема уроку. Розв'язування вправ.

Мета уроку: формування вмінь учнів застосовувати вивчені формули та означення до розв'язування задач.

Тип уроку: комбінований.

Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника» [13], посібник [14].

Вимоги до рівня підготовки учнів: застосовують вивчені формули до розв'язування задач.

Хід уроку

І. Перевірка домашнього завдання

Правильність виконання домашніх завдань учні перевіряють за записами, зробленими на дошці до початку уроку.

Завдання 2. Розв'язання

Оскільки sin²α + cos²α = 1 і sinα = , то  cosα = = = = = .

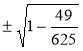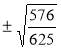Ураховуючи, що 90° < α < 180° і cosα < 0, маємо cosα = , тоді .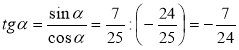

Відповідь. cosα = , tgα = .

Завдання 3. Розв’язання

sin⁴α + sin²αcos²α – sin²α + 1 = (sin⁴α + sin²αcos²α) – sin²α + 1 = sin²α(sin²α +  + cos²α) – sin²α + 1 = sin²α · 1 – sin²α+1 = sin²α – sin²α + 1 = 1.

Відповідь. 1.

Фронтальне опитування

1. Сформулюйте означення sinα, cosα, tgα, якщо α — тупий кут.
2. Запишіть основну тригонометричну тотожність.
3. Запишіть формули для знаходження значення тригономе­тричних функцій тупих кутів.

II. Закріплення й осмислення матеріалу

Виконання вправ

1. Доведіть тотожність:

а) 1 + sin²α + cos²α = 2;   б) 1 – sin²α – cos²α = 0;

в) 2sin²α + cos²α – 1 = sin²α;  г) (1 – cosα)(1 + cosα) = sin²α;

д) sin⁴α – cos⁴α + 1 = 2sin²α.

2. Знайдіть:

а) cosα і tgα, якщо sinα = 0,6 і 90° < α < 180°;

б) sinα і tgα, якщо cosα = і 90° < α < 180°.

III. Самостійна робота

Самостійну роботу навчального характеру можна провести за посібником [14], тест 1 «Тригонометричні функції кутів від 0° до 180°».

Наприкінці уроку слід зібрати зошити для перевірки само­стійної роботи.

IV. Домашнє завдання

1. Вивчити формули та значення тригонометричних функцій деяких кутів (табл. 1).
2. Розв'язати задачі.

1) Знайти sinα і tgα, якщо cosα = -0,6 і 90° < α < 180°.

2) Скоротити вираз:

а) 1 – sin²α;  б) (1 – sinα)(1 + sinα);

в) 2cos²αsin²α + cos⁴α + sin⁴α.

V. Підбиття підсумків уроку

Завдання класу

1. Запишіть основну тригонометричну тотожність.
2. Чи можуть одночасно справджуватися рівності:

а) cosα = і sinα = ; б) sinα = і cosα = – ?

3. Визначте знак виразу:
   а) sin 141° cos141° tg141°; б)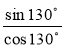 + tg 130°.