Наслідки з теореми про вписаний кут. Розв'язування задач
Тема. Наслідки з теореми про вписаний кут. Розв'язування задач
Мета: домогтися засвоєння учнями змісту наслідків із теореми про вписаний кут та способів їх доведення. Сформувати вміння:
- відтворювати зміст вивчених тверджень;
- знаходити на рисунку об'єкти, властивість яких описується цими наслідками;
- використовувати вивчені твердження під час розв'язування задач на обчислення кутів у колі.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: конспект «Кути в колі».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірку опанування учнями способів дій, вивчених на попередніх уроках, можна провести у формі самостійної роботи.
 Самостійна робота
Самостійна робота
Варіант 1
- Вершини трикутника ABC ділять коло у відношенні 2:3:4. Знайдіть кути цього трикутника.
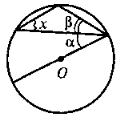
- За рисунком знайдіть кут х (О — центр кола), α = 21°, β = 49°.
 Варіант 2
Варіант 2
- Вершини трикутника ABC ділять коло у відношенні 1:3:5. Знайдіть кути цього трикутника.
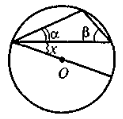
- За рисунком знайдіть кут х (О — центр кола), α = 19°, β = 47°.
III. Формулювання мети і завдань уроку
Задача. Три футболісти пробивають штрафні удари по воротах із точок А, В і С (рис. 1). У кого з них кут обстрілу воріт найбільший?
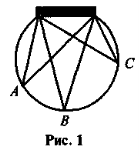 Під час обговорення розв'язання задачі необхідно перейти до її математичної моделі та сформулювати проблему (як порівняти вписані кути, що спираються на одну й ту саму дугу?)
Під час обговорення розв'язання задачі необхідно перейти до її математичної моделі та сформулювати проблему (як порівняти вписані кути, що спираються на одну й ту саму дугу?)
Зрозуміло, що розв'язання цієї проблеми у вигляді деякого правильного твердження для вписаних кутів із наступним доведенням цього твердження, а також оволодіння способами застосування цього твердження і є основною метою уроку.
IV. Актуалізація опорних знань
Фронтальна бесіда
- Вершина кута лежить на колі. Чи обов'язково цей кут є вписаним у коло?
- Сторони кута перетинають коло. Чи обов'язково цей кут є вписаним у коло? Чи може цей кут бути центральним кутом?
- АВ і ВС — хорди кола із центром у точці О. Що можна сказати про кут ABC і АОС? Запишіть правильну рівність для градусних мір цих кутів.
- Точки А і В лежать на колі. Вписаний кут АСВ дорівнює 90°. Чим є хорда АВ?
V. Засвоєння знань
План вивчення матеріалу
- Наслідок 1.
- Наслідок 2.
- Наслідок 3.
4*. Додаткові наслідки. Кути в колі.
Зміст та послідовність вивчення наслідків теореми про вписаний кут логічно обумовлені: наслідок 1 (про вписані кути, що спираються на одну й ту саму дугу) ґрунтується безпосередньо на твердженні теореми про вписаний кут. Доведення наслідку 2 (про вписаний кут, що спирається на півколо) можна розглядати як особливий випадок наслідку 1 (коли дуга кола має градусну міру 180°). Що стосується наслідку 3 (про центр кола, описаного навколо прямокутного трикутника, та довжину медіани прямокутного трикутника, проведеної до гіпотенузи), то доведення цього твердження стає очевидним під час розгляду рисунка до наслідку 2 (див. рис. 64 підручника). Після доведення наслідку 3 бажано розглянути цікавий факт для прямокутного трикутника (медіана прямокутного трикутника, проведена до гіпотенузи, ділить прямий кут на кути, що дорівнюють гострим кутам прямокутного трикутника), який бажано зафіксувати в зошитах учнів як опорний факт. Зміст основних наслідків з теореми про вписаний кут міститься в конспекті «Кути в колі».
|
Конспект 9 |
|
|
Кути в колі |
|
|
|
|
|
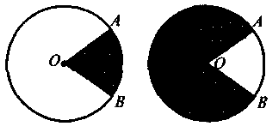
Центральний кут вимірюється дугою, на яку він спирається |
Вписаний кут вимірюється половиною дуги, на яку він спирається, і дорівнює половині центрального кута, що спирається на ту саму дугу |
|
|
|
|
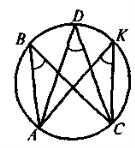
Вписані кути, які спираються на одну й ту саму дугу, рівні між собою |
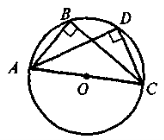
Вписаний кут, який спирається на діаметр, дорівнює 90° |
|
|
|
|
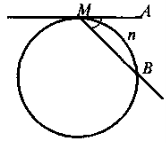
MA — дотична, MB — січна
|
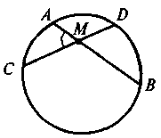
AB і CD — хорди
|
VI. Формування первинних умінь
Виконання усних вправ
- Чи можуть два вписані кути дорівнювати один одному, якщо вони не спираються на одну дугу?
- Чи можуть вписані кути ABC і АВ, С не дорівнювати один одному? Наведіть приклад.
- Чи може: а) кут, сторони якого перетинають коло в кінцях діаметра, бути гострим; б) кут із вершиною на колі, сторони якого перетинають коло в кінцях діаметра, бути гострим?
-
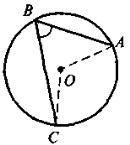
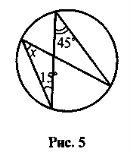
Дано: АВ — діаметр, АС = AD (рис. 2). Доведіть, що
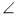 1 =
1 = 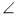 2.
2.
-
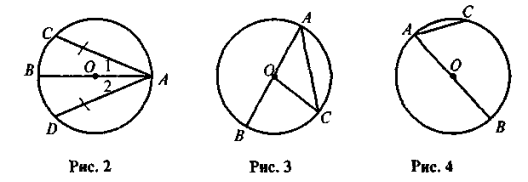
Дано: АВ — діаметр, АС — хорда (рис. 3). Доведіть, що
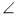 BOC = 2
BOC = 2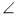 BAC.
BAC.
- Дано: О — центр кола, АС = АО (рис. 4). Знайдіть кут ВАС.
Виконання письмових вправ
-
Трикутник ABC вписаний у коло, центр якого лежить на відрізку АВ. а) Знайдіть кут В, якщо
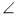 A = 65°. б) Знайдіть медіану, проведену з вершини С, якщо АВ = 12 см.
A = 65°. б) Знайдіть медіану, проведену з вершини С, якщо АВ = 12 см.
- За даними рисунка 5 знайдіть кут х (точка О — центр кола).
-
На колі позначено точки А, В і С, причому АС — діаметр кола,
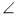 BCA = 60°, ВС = 4 см. Знайдіть радіус кола.
BCA = 60°, ВС = 4 см. Знайдіть радіус кола.
4* (опорна). Кут між хордою і дотичною до кола, проведеною через кінець хорди, вимірюється половиною дуги, яка лежить усередині цього кута. Доведіть.
5* (опорна), а) Дуги кола, які містяться між двома паралельними хордами, рівні. Доведіть, б) Рівні хорди стягують дуги з однаковою градусною мірою, і навпаки: дуги з однаковою градусною мірою стягуються рівними хордами. Доведіть.
VII. Підсумки уроку
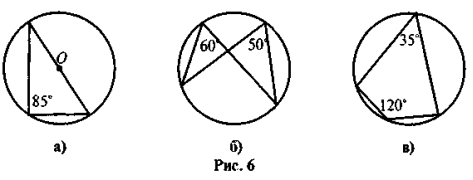
Знайдіть на рисунку 6 помилки.
VIII. Домашнє завдання
Вивчити зміст наслідків. Розв'язати задачі.
-
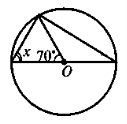 Гіпотенуза прямокутного трикутника дорівнює 10. Чи може висота, проведена до неї, дорівнювати 6? Відповідь обґрунтуйте.
Гіпотенуза прямокутного трикутника дорівнює 10. Чи може висота, проведена до неї, дорівнювати 6? Відповідь обґрунтуйте.
- За даними рисунка знайдіть кут х (точка О — центр кола).
- Знайдіть менший катет прямокутного трикутника, якщо його медіана дорівнює 9 см і утворює з гіпотенузою кут 60°.


про публікацію авторської розробки
Додати розробку