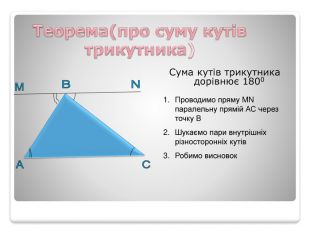
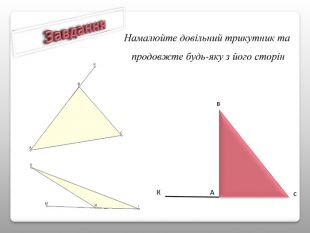
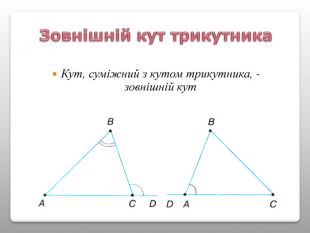
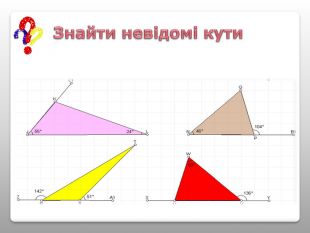
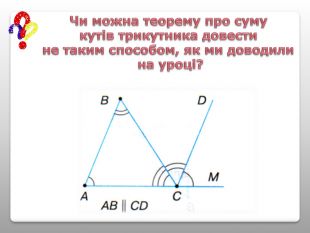
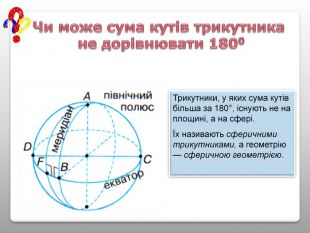
Презентація "Властивості кутів трикутника"
Про матеріал
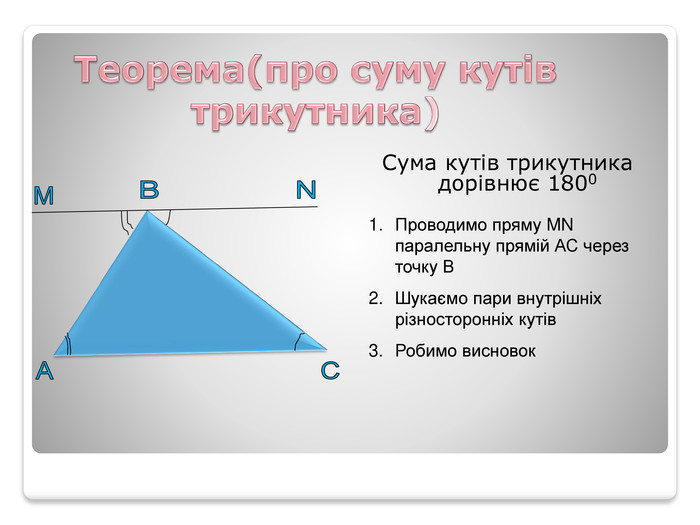
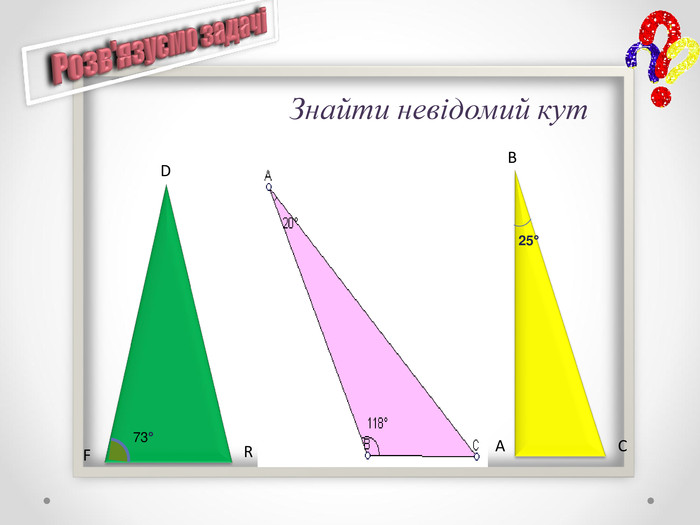
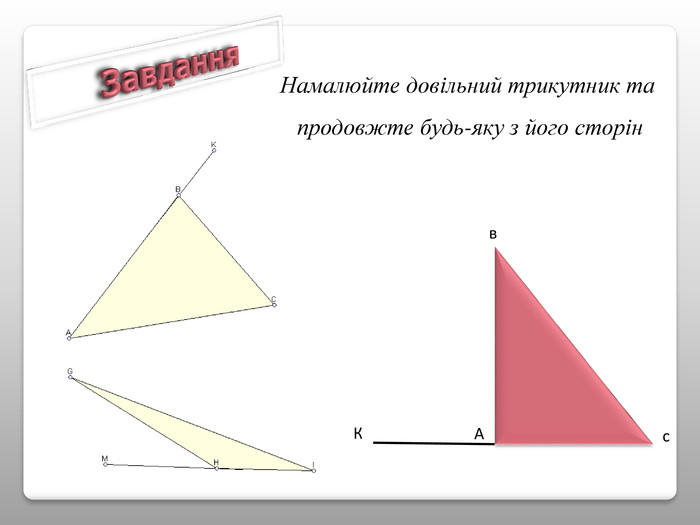
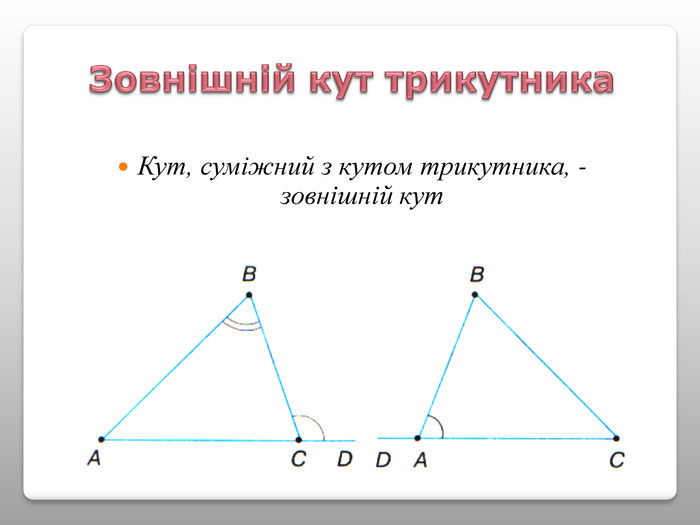
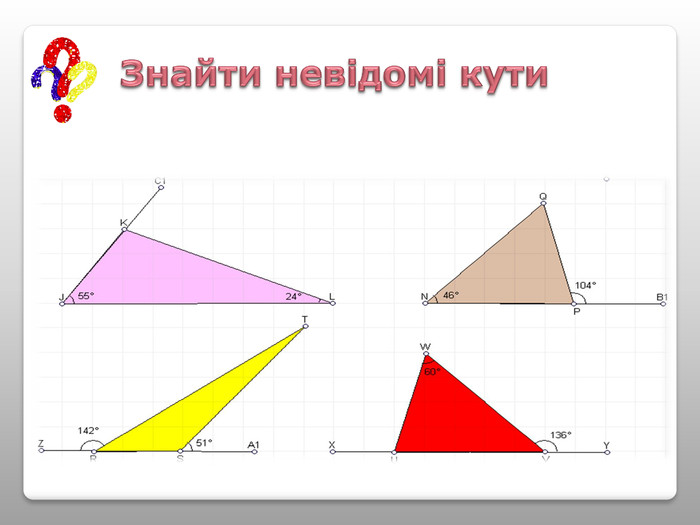
Презентація теми “Властивості кутів трикутника” містить необхідний матеріал для проведення уроку (проблемні питання, практична робота, графічні задачі для первинного закріплення вивченого матеріалу) Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку