Наукова робота з математики
Міністерство освіти і науки України
Департамент освіти і науки Полтавської облдержадміністрації
Управління освіти виконавчого комітету Полтавської міської ради
Полтавське територіальне відділення МАН України
Полтавське міське наукове товариство учнів «Мала академія наук»
Відділення: математики
Секція: прикладної математики
Стрічка Мебіуса та її незвичайні властивості
Роботу виконала:
Піскова Катерина Сергіївна
учень 11-А класу
Комунальний заклад
«Полтавська загальноосвітня школа
І-ІІІ ступенів №34 Полтавської
міської ради Полтавської області»
Науковий керівник:
Крупка Олена Валентинівна
учитель математики
вищої категорії
Полтавської ЗОШ №34
Полтава-2018
Тези
Науково-дослідницької роботи «Стрічка Мебіуса та її незвичайні властивості». Автор: Піскова Катерина Сергіївна, учениця 11-А класу Полтавської ЗОШ № 34 Полтавського територіального відділення МАН України. Науковий керівник: Крупка Олена Валентинівна, учитель математики вищої категорії Полтавської ЗОШ №34.
Мета нашого дослідження – ознайомитись з стрічкою Мебіуса та вивчити її властивості, поглибити свої знання з топології, як розділу математики. Показати особливості цієї загадкової геометричної фігури та велике практичне застосування в науці, техніці, мистецтві та інших галузях.
Для досягнення цієї мети нами вирішувались наступні завдання:
- дослідити задачі, що спонукали до появи такої науки як топологія;
- вивчити основні поняття і аксіоматику розділу « Топологія»;
- ознайомитись з біографією Мебіуса та інших вчених математиків та їх науковими працями;
- описати властивості топологічних об`єктів;
- систематизувати інформацію про стрічку Мебіуса та дослідити її властивості;
- зібрати інформацію та розглянути приклади практичного застосування цієї фігури в науці, техніці і навіть в мистецтві;
- провести досліди зі стрічкою Мебіуса;
- обґрунтувати актуальність і важливість обраної теми.
Дані завдання розв`язуються методами комплексного аналізу, аналітично-описово та експериментально.
Результати дослідження: визначили властивості стрічки Мебіуса, яка має лише одну поверхню ,якщо рухатися по цій поверхні, то неможливо дістатись кінця; зібрали інформацію про практичне застосування цієї фігури ;описали і вивчили розділ математики- топологія, який ще доволі молодий та має перспективу подальшого дослідження.
ЗМІСТ
ВСТУП………………………………………………………………………… 5
РОЗДІЛ 1. Задачі, що призвели до появи топології………………………… 8
- Проблема чотирьох фарб………………………………………………..8
1.2 Геометрія гумової плівки……………………………………………… 9
1.3Ще одна легенда з сивої давнини……………………………………… 10
РОЗДІЛ 2. Топологія як наука та її властивості……………………………... 13
РОЗДІЛ 3. Стрічка Мебіуса……………………………………………………17
3.1 Що ж таке стрічка Мебіуса?...................................................................18
3. 2Властивості стрічки Мебіуса……………………………………… 19
3.3 Наукове використання……………………………………………… 20
3.4 Джерело творчого натхнення……………………………………… 22
3.5 Лист Мебіуса в техніці……………………………………………… 23
РОЗДІЛ 4.Дослідження властивостей стрічки Мебіуса……………….… 26
4.1 Досліди з листом Мебіуса…………………………………………… 26
4.2 Робимо самі, своїми руками!................................................................ 27
ВИСНОВКИ…………………………………………………………………… 28
Список використаних джерел…………………………………………………30
ВСТУП
У повсякденній роботі і в процесі наукових досліджень людина весь час міркує, прагнучи із уже відомих їй знань дістати нові. В цьому полягає процес еволюції, руху вперед, а також специфіка вивчення математики. У своїй роботі ми прагнули дослідити досить молодий розділ математики- топологію, зокрема на прикладі такої незвичайної фігури як стрічка Мебіуса.
Об`єкт дослідження - топологія та стрічка Мебіуса.
Предмет дослідження - математичне моделювання, властивості та прикладне застосування стрічки Мебіуса.
Мета нашого дослідження – ознайомитись з стрічкою Мебіуса та вивчити її властивості, поглибити свої знання з топології, як розділу математики. Показати особливості цієї загадкової геометричної фігури та велике практичне застосування в науці, техніці, мистецтві та інших галузях.
Для досягнення цієї мети нами вирішувались наступні завдання:
- дослідити задачі, що спонукали до появи такої науки як топологія;
- вивчити основні поняття і аксіоматику розділу « Топологія»;
- ознайомитись з біографією Мебіуса та інших вчених математиків та їх науковими працями;
- описати властивості топологічних об`єктів;
- систематизувати інформацію про стрічку Мебіуса та дослідити її властивості;
- зібрати інформацію та розглянути приклади практичного застосування цієї фігури в науці, техніці і навіть в мистецтві;
- провести досліди зі стрічкою Мебіуса;
- обґрунтувати актуальність і важливість обраної теми.
Методами дослідження ми обрали: наукова абстракція, метод факторного аналізу, синтезу та прогнозування. Тема « Дослідження стрічки Мебіуса» актуальна в наш час, так як саме на листі Мебіуса можна спостерігати такі властивості, як зв`язність, неперервність, неорієнтовність, односторонність, а також хроматичне число, що дорівнює 6.
Практична значущість та актуальність роботи полягає в необхідності вивчення властивостей стрічки Мебіуса та, її різноманітного використання.
Топологія- один із найсучасніших і молодих розділів математики. Історія її розвитку налічує всього декілька століть. Властивості геометричних фігур, які не змінюються при їх деформаціях, і вивчає топологія.
Задача Семи мостів Кенігсбергу є показовою при вивченні математики, також вона дала поштовх до створення розділу математики, що називається теорія графів. Ейлер показав, що всі ребра графа можна обійти лише по одному разу по неперервному замкненому маршруту, якщо граф містить тільки парні вершини.
В даний час проблеми топології посилено розробляються математиками багатьох країн. Топологічні простори природно з'являються в багатьох розділах математики. Це робить топологію надзвичайно універсальним інструментом для математиків. Щоб зрозуміти, для чого потрібна топологія, можна навести такий приклад: в деяких геометричних задачах не так важливо знати точну форму об'єктів, як знати як вони розташовані.
Відомий і таємничий листок Мебіуса винайшов 1858 року німецький геометр Август Фердінанд Мебіус, учень «короля математиків» Карла Гаусса. Так, аж до 1858 року вважалося, що будь-яка поверхня повинна мати дві сторони. Однак Йоганн Бенедикт Лістинг і Август Фердинанд Мебіус відкрили геометричний об'єкт, у якого була всього одна сторона, і описали його властивості.
Практично кожній людині відомо поняття стрічки Мебіуса. У цього тривимірного вигнутого плоского об'єкта є лише одна сторона та грань, що дуже важко піддається розумінню людьми з погано розвиненим просторовим уявою. А нещодавно групі вчених з Кільського університету (Kiel University), очолюваної професором хімії Рэйнером Херджесом (Rainer Herges), вперше в історії науки вдалося синтезувати складну молекулу, структура якої являє собою відразу потрійну стрічку Мебіуса. І слід зауважити, що вчені зробили це не заради розваги, такі молекули володіють набором унікальних квантово-механічних властивостей, які можна використовувати в областях молекулярної електроніки та оптоелектроніки.
РОЗДІЛ 1
Задачі, що призвели до появи топології
Топологія- один із найсучасніших і молодих розділів математики. Історія її розвитку налічує всього декілька століть. Спробуємо дослідити шлях створення цієї цікавої науки.
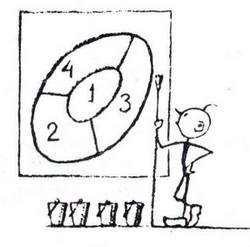
1.1 Проблема чотирьох фарб
Видатний фізик Макс Борн у спогадах про свого вчителя, відомого математика Германа Міньковського, наводить такий епізод: «Мінковський почав розповідь про нову математичну дисципліну з викладу так званої проблеми чотирьох кольорів. При виготовленні географічних карт з’ясувалося, що для зафарбовування будь-якої карти так, щоб дві сусідні країни були різні за кольором, необхідно і цілком достатньо мати чотири кольори(Рис.1.1).
 (Рис.1.1)
(Рис.1.1)
Він додав: «На жаль, це не вдалося довести. Але цим займалися тільки математики третього рангу. Я сподіваюся цей доказ отримати», і тут він почав свої дедукції… Минуло два-три тижні, справа все ускладнювалася; і навіть через три-чотири тижні рішення не було. Коли ми одного ранку зібралися в аудиторії, вибухнула сильна гроза, виблискували блискавки, лив дощ. У той момент, коли Мінковський входив в аудиторію, пролунав страшний удар грому. Мінковський спокійно пройшов до кафедри і сказав цілком серйозно: «Небо гнівається на мою зухвалість: мій доказ проблеми чотирьох кольорів теж невірний». Потім по його обличчю пробігла усмішка, і він знову приступив до читання лекції».
1.2 Геометрія гумової плівки
Завдання, яке безуспішно намагався вирішити Мінковський, здається, дуже простим. Чимало й інших настільки ж простих на вигляд завдань розглядає особлива математична дисципліна – топологія. Цікаво, що її виникнення пов’язане з рішенням «життєвого» завдання.
 (Рис.1.2)
(Рис.1.2)
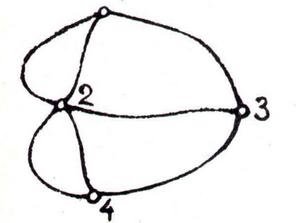
У Кенінсбергу було сім мостів, по яким любили прогулюватися міські жителі. Розповідають, що когось із них зацікавило питання: як вибрати шлях для прогулянки, щоб пройти по всім семи мостах і при цьому жоден з них не перетнути двічі(Рис.1.2). Звістка про цю проблему дійшла до знаменитого математика Ейлера, який в цей час працював у Петербурзі. Ейлер вирішив її в 1735 році, довівши, що неможливо пройти по семи мостах по одному разу.
Однак він зробив більше, ніж просто вирішив завдання про сім мостів. Займаючись проблемою семи мостів, Ейлер зауважив, що у геометричних фігур є властивості, які не залежать від їх розмірів і форми, а залежать тільки від загального розташування крапок і ліній. Наприклад, суть завдання про сім мостів не зміниться, якщо ми замінимо кожну частину суші точкою, а кожен міст – лінією. Тоді ми отримаємо креслення, яке ви бачите на малюнку(Рис.1.3).
 (Рис.1.3)
(Рис.1.3)
Отриману конфігурацію Ейлер назвав графом, точки- його вершинами, а лінії- ребрами. Вершини він розділив на парні та непарні в залежності від того, парне чи непарне число ребер виходе із вершини. Ейлер показав, що всі ребра графа можна обійти лише по одному разу по неперервному замкненому маршруту, якщо граф містить тільки парні вершини. Так як в даному графі містяться тільки непарні вершини, то мости неможливо обійти по неперервному маршруту . А в 1752 р. Ейлер дав строге доведення формули V – E + F = 2, где V– число вершин, E – число ребер и F – число граней. Це співвідношення між числом вершин, ребер та граней многокутника вивів в 1640 р. французький філософ і математик Р.Декарт.
Отже, властивості геометричних фігур, які не змінюються при їх деформаціях, і вивчає топологія. А ця задача Семи мостів Кенігсбергу є показовою при вивченні математики, також вона дала поштовх до створення розділу математики, що називається теорія графів.
1.3Ще одна легенда з сивої давнини…
Завдання топологічного характеру виникали ще багато століть тому. Згідно стародавньої легенди, один халіф був так стурбований кількістю шанувальників своєї прекрасної дочки, що вирішив влаштувати для них випробування. Нареченим пропонувалося завдання: з’єднати однакові цифри на фігурах, які зображені на малюнку, непересічними лініями(Рис.1.4).
 (Рис.1.4)
(Рис.1.4)
Можна бути впевненим, що якби халіф не пом’якшав, його дочка ніколи не вийшла б заміж, так як це завдання не може бути вирішене. Ще в XIX столітті фізик Кірхгоф зрозумів важливість топологічних досліджень для вирішення проблем, що виникають при вивченні розгалужених електричних ланцюгів.
Цікаво, що багато важливих явищ у фізиці виявилися пов’язаними з такими ж настроями, як і ті, що фігурують в задачі халіфа. Ймовірно, самою знаменитою невирішеною проблемою після відомої теореми Ферма і, звичайно, найпростішою з вигляду є проблема чотирьох фарб, яку намагався вирішити Мінковський.
Парадоксально, що хоча проблема не була вирішена для карти, намальованої на площині або на поверхні глобуса, вона була вирішена для набагато більш складних поверхонь. Наприклад, доведено, що сім фарб необхідно і достатньо для розфарбовування будь-якої карти, намальованої на поверхні тора (фігури, що має вигляд «бублика»)(Рис.1.5)
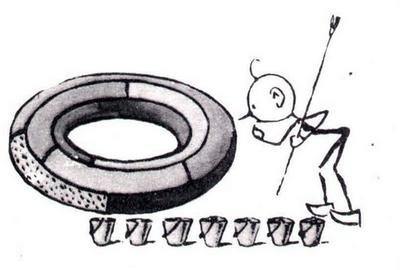 (Рис.1.5)
(Рис.1.5)
В даний час проблеми топології посилено розробляються математиками багатьох країн.
РОЗДІЛ 2
Топологія як наука та її властивості
Власне термін «топологія» («topologie» німецькою мовою) вперше з'явився лише в 1847 р. у статті Лістінга Vorstudien zur Topologie. Однак на той час Лістінг вже понад 10 років використовував цей термін в своїх листуваннях. «Topology», англійська форма терміну, була запропонована в 1883 в журналі Nature для того, щоб розрізнити якісну геометрію від геометрії звичайної, в якій превалюють кількісні співвідношення. Слово topologist — тобто тополог, в розумінні «спеціаліст з топології» було вперше використано в 1905 в журналі Spectator. Також топологія тривалий час була відома ще під назвою Analysis Situs (лат. аналіз місця). Засновниками сучасної топології є Г.Кантор (1845-1918), А.Пуанкаре (1854-1912) та Л.Брауер (1881-1966).
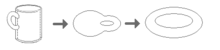
Топологічні простори природно з'являються в багатьох розділах математики. Це робить топологію надзвичайно універсальним інструментом для математиків. Щоб зрозуміти, для чого потрібна топологія, можна навести такий приклад: в деяких геометричних задачах не так важливо знати точну форму об'єктів, як знати як вони розташовані. Якщо розглянути квадрат і коло (контури), здавалося б такі різні фігури, можна помітити дещо спільного: обидва об'єкти є одновимірними та обидва розділяють простір на дві частини — внутрішність та зовнішність. Наведемо дуже поширений приклад з чашкою(Рис.2.1).
 (Рис.2.1) Неперервна деформація кавової чашки в бублик (тор). Таке перетворення називають гомотопією.
(Рис.2.1) Неперервна деформація кавової чашки в бублик (тор). Таке перетворення називають гомотопією.
Фази перетворення чашки в бублик)(Рис.2.2).
Інтуїтивно, два топологічних простори є еквівалентними (гомеоморфними), якщо один може бути перетворений в інший без відрізань або склеювань. Традиційним є такий жарт: тополог не може відрізнити чашку кави, з якої вона п'є, від бублика, який він їсть, оскільки достатньо гнучкий бублик можна легко перетворити у форму чашки, створивши заглиблення і збільшуючи його, водночас зменшуючи дірку до розмірів ручки.
Як просте початкове завдання можна класифікувати літери Латинської абетки в термінах топологічної еквівалентності. (Будемо вважати, що товщина ліній, з яких складено літери ненульова.) В більшості шрифтів що зараз застосовуються існує клас літер рівно з однією діркою: {a, b, d, e, o, p, q}, клас літер без дірок: {c, f, h, k, l, m, n, r, s, t, u, v, w, x, y, z}, та клас літер, що складаються з двох шматків: {i, j}. Літера «g» може належати або класу літер з однією діркою, або (в деяких шрифтах) це може бути літера з двома дірками (якщо її хвостик був замкнений). Для складнішого прикладу можна розглянути випадок нульової товщини ліній; можна розглянути різні топології в залежності від того, який шрифт обрати. Топологія літер має своє практичне застосування в трафаретній типографії: наприклад, шрифт Braggadocio може бути вирізаний з площини, не розпавшись після цього.
Аксіоматика топології побудована на засадах теорії множин, але провідну роль у дослідженнях з сучасної топології відіграють насамперед алгебраїчні і геометричні методи. Об'єктами дослідження топології є топологічні простори, спільне узагальнення таких структур як граф, поверхня у тривимірному просторі і множина Кантора, та відображення між ними. При цьому досліджуються властивості топологічних просторів як в малому (локальні), так і в цілому (глобальні). Серед різноманітних напрямків топології відзначимо наближену до теорії множин загальну топологію, яка вивчає такі загальні властивості абстрактних топологічних просторів як компактність або зв'язність, та алгебраїчну топологію, яка намагається описати топологічні простори за допомогою їхніх алгебраїчних інваріантів, наприклад чисел Бетті та фундаментальної групи. Геометрична топологія вивчає топологічні простори геометричного походження, зокрема вузли у тривимірному евклідовому просторі і тривимірні многовиди. До геометричної топології належить одна із найвизначніших і найвідоміших математичних проблем, гіпотеза Пуанкаре, яку нарешті (2003 р.) довів російський математик Григорій Перельман.
Поряд з алгеброю і геометрією, топологічні методи широко використовуються у функціональному аналізі, теорії динамічних систем і сучасній математичній фізиці.
Математична спільнота високо відзначила внесок топологів до розвитку математики. За період з 1936 по 2006 р., одна з найвищих відзнак у математиці, Медаль Філдса, була присуджена 48 математикам, 9 з них за дослідження саме у топології. У роботах ще декількох з лауреатів топологічні методи відігравали важливу роль.
- 2006 Григорій Перельман
- 1990 Едвард Віттен
- 1986 Майкл Фрідман
- 1982 Вільям Терстон
- 1970 Сергій Новіков
- 1966 Стівен Смейл
- 1966 Майкл Атія
- 1966 Олександр Гротендік
- 1962 Джон Мілнор
- 1958 Рене Том
- 1954 Жан-П'єр Серр
- 1936 Ларс Альфорс
Трьом з них премія була присуджена за розв'язання гіпотези Пуанкаре: Григорію Перельману за доведення оригінальної гіпотези стосовно тривимірної сфери, і Майклу Фрідману і Стівену Смейлу — за розв'язання аналогічного питання у чотирьох (Фрідман) і п'яти та більше вимірах (Смейл). Цікаво, що ще дві з Філдсовських премій було присуджено за результати про сфери: Джону Мілнору за відкриття 28 диференційовних структур на семивимірній сфері, та Жану-П'єру Серру за розробку методів обчислення гомотопічних груп сфер. Таким чином, п'ять з сорока восьми Філдсівських премій одержали дослідники сфер!
Отже, тополо́гія (грец. τόπος — місце, logos — наука) — розділ математики, який наближений до геометрії. У той час як алгебра починається з розглядання операцій, геометрія — фігур, а математичний аналіз — функцій; найфундаментальніше поняття топології — неперервність.
РОЗДІЛ 3
Стрічка Мебіуса
Не слід плутати те , що нам здається неймовірним і неприродним, з абсолютно неможливим.
К. Ф.Гаусс
 (Рис.3.1)
(Рис.3.1)
Август Фердінанд Мебіус
(1790-1868)
Відомий і таємничий листок Мебіуса винайшов 1858 року німецький геометр Август Фердінанд Мебіус(Рис.3.1), учень «короля математиків» Карла Гаусса. Мебіус починав як астроном. Того часу заняття математикою не знаходило належної підтримки, астрономія ж давала достатньо коштів, щоб не думати про них, і залишала вдосталь часу для власних роздумів. Мебіус став одним із найвидатніших геометрів XIX ст. У віці 68 років він зробив відкриття неймовірної краси — листок Мебіуса.
 (Рис.3.2)
(Рис.3.2)
3.1 Що ж таке стрічка Мебіуса?
Стрічка Мебіуса - загадка сучасності. Існують наукові знання і явища, які привносять в буденність нашого життя таємницю і загадку. Стрічка Мебіуса відноситься до них повною мірою.
Сучасна математика чудово описує за допомогою формул всі її властивості та особливості. Що це таке? Стрічка Мебіуса, яку також називають петлею, поверхнею або листом, - це об'єкт вивчення такої математичної дисципліни, як топологія, що досліджує загальні властивості фігур, що зберігаються при таких безперервних перетвореннях, як скручування, розтяг, стиск, згинання та інших, не пов'язаних з порушенням цілісності .
Дивовижною і неповторною особливістю такої стрічки є те, що вона має всього одну сторону і край ,які ніяк не пов'язані з її розташуванням в просторі. Лист Мебіуса є топологічним, тобто безперервним об'єктом з найпростішої односторонньої поверхнею з кордоном в звичайному Евклідовому просторі (3-вимірному), де можливо з однієї точки такій поверхні, не перетинаючи краю, потрапити в будь-яку іншу.
Такий непростий об'єкт, як стрічка Мебіуса, був і відкритий досить незвично. Насамперед відзначимо, що два математика, абсолютно не зв'язані між собою в дослідженнях, відкрили її одночасно - в 1858 році. Ще одним цікавим фактом є те, що обидва цих учених в різний час були учнями одного і того ж великого математика - Йоганна Карла Фрідріха Гаусса.
Так, аж до 1858 року вважалося, що будь-яка поверхня повинна мати дві сторони. Однак Йоганн Бенедикт Лістинг і Август Фердинанд Мебіус відкрили геометричний об'єкт, у якого була всього одна сторона, і описують його властивості.
Стрічка була названа на честь Мебіуса, а ось батьком-засновником «гумовою геометрії» топологи вважають Лістинга і його працю «Попередні дослідження по топології». Топологічно, стрічка Мебіуса може бути визначена як квадрат [0,1] x [0,1], верх якого з'єднаний з низом у співвідношенні (x, 0) ~ (1-x, 1) for 0 ≤ x ≤ 1
Тісно пов'язаним з стрічкою Мебіуса є загадковий об'єкт - пляшка Кляйна (Додаток А). Пляшка Кляйна може бути створена склеюванням двох стрічок Мебіуса один з одним уздовж їх кордонів. Ця операція не може бути здійснена в тривимірному просторі без створення перетинів всередині фігури.
Одна з базових неможливих фігур неможливий трикутник може бути представлений як стрічка Мебіуса, якщо згладити деякі його межі. При цьому вийде стрічка Мебіуса, що описує три витка.
3.2Властивості стрічки Мебіуса
Стрічці Мебіуса притаманні такі властивості, які не змінюються при її стисканні, розрізуванні уздовж або згинанні:
1. Наявність одного боку. Перевірити це досить просто: беремо стрічку або лист Мебіуса і намагаємося зафарбувати внутрішню сторону одним кольором, а зовнішню - іншим. Не має значення, в якому місці і напрямку було розпочато фарбування, вся фігура буде зафарбована одним кольором.
2. Безперервність виражається в тому, що будь-яку точку цієї геометричної фігури можна з'єднати з будь-якою іншою її точкою, не перетинаючи кордону поверхні Мебіуса.
3. Зв'язність, або двомірність, полягає в тому, що при розрізанні стрічки вздовж, з неї не вийде кілька різних фігур, і вона залишається цілісною.
4. У ній відсутня така важлива властивість, як орієнтованість. Це означає, що людина, що йде по цій фігурі, повернеться до початку свого шляху, але тільки в дзеркальному відображенні самого себе. Таким чином, нескінченна стрічка Мебіуса може призвести до вічної подорожі.
5. Особливий хроматичний номер, який показує, яке максимально можливе число областей на поверхні Мебіуса, можна створити так, щоб у будь-який з них був спільний кордон з усіма іншими. Стрічка Мебіуса має хроматичний номер – 6.
3.3 Наукове використання
Сьогодні лист Мебіуса і його властивості широко застосовуються в науці, та є основою для побудови нових гіпотез і теорій, проведення досліджень і експериментів, створення нових механізмів і пристроїв. Так, існує гіпотеза, згідно з якою Всесвіт - це величезна петля Мебіуса. Побічно про це свідчить і теорія відносності Ейнштейна, згідно з якою навіть полетів прямо корабель може повернутися в ту ж тимчасову і просторову точку, звідки стартував. Якщо космічний корабель летітиме весь час прямо, нікуди не звертаючи, то чи буде він ще більше віддалятися від Землі? «Не обов `язково, -- вирішив Енштейн. Корабель може повернутися, навіть якщо він летить прямо.»
Якщо корабель подорожує ніби по стрічці Мебіуса, то відбувається дещо дивне. Півоберта, на які перекручено лист ніби перевертають корабель на іншу сторону: повернувшись в початок подорожі, він виявляє у себе серце не ліворуч, а праворуч!
Якщо наш простір нагадує лист Мебіуса, то повернувшись на Землю, астронавт може виявитись власним дзеркальним відображенням. Але поки що це лише гіпотеза. Відповідь залежить від того, яка маса Всесвіту, бо саме вона призводить до викривлення простору - чим більше маса, тим більше й кривизна.
Інша теорія розглядає ДНК як частину поверхні Мебіуса, що пояснює складнощі з прочитанням і розшифровкою генетичного коду. Крім усього іншого, така структура дає логічне пояснення біологічної смерті - замкнута на самій собі спіраль призводить до самознищення об'єкта. На думку фізиків, багато оптичних законів грунтуються на властивостях листа Мебіуса. Так, наприклад, дзеркальне відображення - це особливе перенесення в часі і людина бачить перед собою свого дзеркального двійника.
Реалізація на практиці. У різних галузях промисловості стрічка Мебіуса застосування знайшла вже давно. Великий винахідник Нікола Тесла на початку століття винайшов резистор Мебіуса, що складається з двох скручених на 1800 провідних поверхонь, який може протистояти потоку електричного струму без створення електромагнітних завад. На основі досліджень поверхні стрічки Мебіуса і її властивостей було створено безліч пристроїв та приладів. Її форму повторюють при створенні смуги стрічкового конвеєра і фарбувальної стрічки в друкованих пристроях, абразивних ременів для заточування інструментів і автоматичної передачі. Це дозволяє значно збільшити термін їх служби, так як зношування відбувається більш рівномірно. Не так давно дивні особливості листа Мебіуса дозволили створити пружину, яка, на відміну від звичайних, що спрацьовують в протилежному напрямку, не міняє напрямок спрацьовування. Застосовується вона в стабілізаторі рульового приводу штурвала, забезпечуючи повернення колеса керма в початкове положення.
Крім того, знак стрічка Мебіуса використовується в різноманітних торгових марках і логотипах. Найвідоміший з них - це міжнародний символ вторинної переробки. Його проставляють на упаковках товарів або придатних для подальшої переробки, або зроблених з перероблених ресурсів.
3.4 Джерело творчого натхнення.
Стрічка Мебіуса і її властивості лягли в основу творчості багатьох художників, письменників, скульпторів і кінематографістів. Найвідоміший художник, котрий використовував в таких своїх роботах, як «Стрічка Мебіуса II (Червоні мурашки)», «Вершники» і «Вузли», стрічку і її особливості - Мауріц Корнеліс Ешер. Листи Мебіуса, або, як їх ще називають, поверхні мінімальної енергії, стали джерелом натхнення для математичних художників і скульпторів, наприклад, Брента Коллінза або Макса Білла. Найвідоміший пам'ятник стрічці Мебіуса встановлений біля входу в вашингтонський Музей історії та техніки. Російські художники також не залишилися осторонь від цієї теми і створили свої роботи. Скульптури «Стрічка Мебіуса» встановлені в Москві і Єкатеринбурзі. Література і топологія .
Незвичайні властивості поверхонь Мебіуса надихнули багатьох письменників на створення фантастичних і сюрреалістичних творів. Петля Мебіуса відіграє важливу роль у романі Р. Желязни «Двері в піску» і служить як засіб переміщення крізь простір і час для головного героя роману «Некроскоп» Б. Ламли. Фігурує вона і в оповіданнях «Стіна темряви» Артура Кларка, «На стрічці Мебіуса» М. Клифтона і «Лист Мебіус» А. Дж. Дейча. За мотивами останнього режисером Густаво Москера був знята фантастична кінокартина «Мебіус».
3.5 Лист Мебіуса в техніці
Стрічка Мебіуса використовується також в багатьох пристроях. Наприклад абразивні ремені для заточки інструментів, фарбуюча стрічка в друкарських пристроях(Рис.3.3), в магнітофонних касетах(Рис.3.4), тоді строк використання касети подвоюється(Рис.3.5).
(Рис.3.4)

 (Рис.3.5)
(Рис.3.5) (Рис.3.3)
(Рис.3.3)
А декілька років потому вона ще стала виконувати роль пружини. Як відомо , заведена пружина зпрацьовує в протилежному напрямку. А стрічка Мебіуса всупереч усім законам..напрямку не міняє, подібно до механізмів з двома положеннями. Її не можливо перекрутити, як звичайну- це свого роду вічний двигун.Такий же механізм знадобиться і в конструкції стабілізатора штурвала привода керма, забезпечивши повернення колеса керма в початкове положення. Такий стабілізатор можна створити на валу колеса керма, що зменшить навантаження та спростить конструкцію.
Автомобіль Toyota MOB(Рис.3.6)
 (Рис.3.6)
(Рис.3.6)
Боллід Мебіуса виконаний іспанським дизайнером Хорхе Марті Відала і уособлює в собі красу та загадку стрічки Мебіуса. Виняткова форма кузова забезпечує гоночній машині гарну аеродинаміку.
Резистор Мебіуса(Рис.3.7)
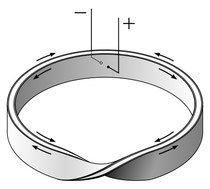 (Рис.3.7)
(Рис.3.7)
Це сучасний електронний елемент, що не має власної індуктивності.
Шлифовальная лента
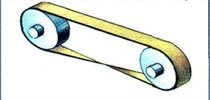 (Рис.3.8)
(Рис.3.8)
В 1969 році радянський винахідник Губайдулін запропонував нескінчену шліфувальну стрічку у вигляді стрічки Мебіуса(Рис.3.8).
А нещодавно групі вчених з Кільського університету (Kiel University), очолюваної професором хімії Рэйнером Херджесом (Rainer Herges), вперше в історії науки вдалося синтезувати складну молекулу, структура якої являє собою відразу потрійну стрічку Мебіуса. І слід зауважити, що вчені зробили це не заради розваги, такі молекули володіють набором унікальних квантово-механічних властивостей, які можна використовувати в областях молекулярної електроніки та оптоелектроніки.
Доречі, фізики стверджують, що всі оптичні закони спираються на стрічку Мебіуса, наприклад, відображення в дзеркалі -це своєрідне перенесення у часі, адже ми бачимо перед собою свого дзеркального двійника.
РОЗДІЛ 4
Дослідження властивостей стрічки Мебіуса
4.1 Досліди з листом Мебіуса
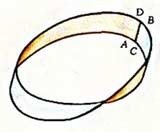
1. Візьмемо стрічку АВСD, розділемо її по ширині на дві однакові частини пунктирною лінією (паралельно сторонам АС і ВD) і, перекрутивши один раз, склеїмо листок Мебіуса. Розріжемо його
ножицями за пунктирною лінією. Ми одержали не два кільця, як можна було сподіватися, а одне: удвічі вужче, але удвічі довше від початкового, і до того воно перекручене не один раз, а двічі.
2. Розріжемо кільце, одержане в першому експерименті, ще раз. Ми одержали два зціплених одне з одним кільця, причому кожне з них двічі перекручене
3. Підготуємо два листки Мебіуса, попередньо розділивши стрічку лініями на чотири і п'ять рівних смуг пунктирними лініями. Розріжемо за цими лініями. Що ми одержали? Що буде, якщо перед склеюванням перевернути стрічку двічі, а потім розрізати вздовж посередині? Ми отримали два зціплених кільця, перекручених таким чином, що нагадали нам два серця…романтично.
4. Тепер виготовимо стрічку Мебіуса, яка перекручена на 3 півоберти (540 градусів) та розріжемо її навпіл. Ми отримали замкнену стрічку у формі трилистника. Приблизно такий вузел з трьома самоперетинами(Рис.4.1).  (Рис.4.1)
(Рис.4.1)
5. А якщо скласти папір як на малюнку(Рис.4.2), потім зкрутити з нього стрічку Мебіуса ( поворот на 360 градусів) та розрізати її навпіл або відступивши третину, то ми отримаємо 3 зціплених між собою кільця.
(Рис.4.2)
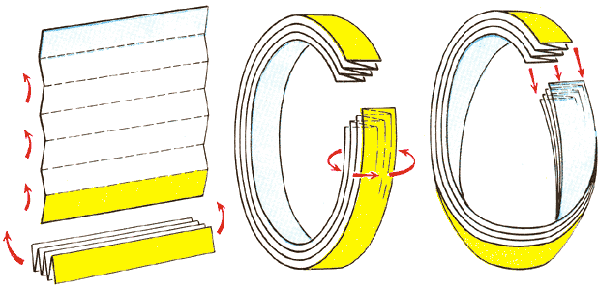
4.2 Робимо самі, своїми руками!
Якщо вас зацікавила стрічка Мебіуса, як зробити її модель, вам підкаже невелика інструкція: 1. Для виготовлення її моделі потрібні: - лист звичайного паперу; - ножиці; - лінійка. 2. Відрізаємо смугу від аркуша паперу так, щоб її ширина була в 5-6 разів менше довжини. 3. Отриману паперову смужку розкладаємо на рівній поверхні. Один кінець притримуємо рукою, а іншою повертаємо на 180 градусів так, щоб смуга перекрутилася і виворіт стала лицьовою стороною. 4. Склеюємо кінці перекрученої смуги так, як показано на малюнку. Стрічка Мебіуса готова.
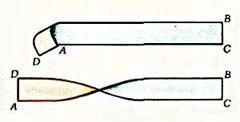
5. Візьміть ручку або маркер і посередині стрічки почніть малювати доріжку. Якщо ви зробили все правильно, то повернетеся в ту ж точку, звідки почали креслити лінію. Для того, щоб отримати наочне підтвердження того, що стрічка Мебіуса - односторонній об'єкт, олівцем або ручкою спробуйте зафарбувати яку-небудь її сторону. Через деякий час ви побачите, що зафарбували її повністю.
6.А тепер поміркуємо, чи з будь-якої стрічки можна виготовити лист Мебіуса? Адже не кожну полоску можна зкрутити як цю стрічку. Наприклад, з квадратного листа паперу лист Мебіуса не вийде. Тоді яке ж мінімальне відношення довжини до ширини стрічки має бути? Нехай ширина полоски дорівнює умовній 1. Тоді виявляється, що мінімальна довжина полоски дорівнює приблизно 1,73. Отримане значення дорівнює другому «золотому перерізу». Це ще одна загадкова властивість стрічки Мебіуса.
Отже, проведені дослідження ще раз довели, що стрічка Мебіуса - тривимірна поверхня, що має тільки одну сторону і одну межу, що володіє математичною властивістю неорієнтованості.
ВИСНОВКИ
- В науковій роботі описано причини виникнення топології як одного з розділів математики .
- Розглянуто задачі, що спонукали до становлення топології та вчених, що займались цим питанням.
- Описано стрічку Мебіуса як топологічний об`єкт та проаналізовано загадкові властивості цієї фігури.
- Досліджено застосування стрічки Мебіуса в різних галузях науки і техніки та навіть в мистецтві.
- Відзначено, що ця галузь математики доволі молода і знаходиться в стадії розвитку. Тому є необхідність в подальшому вивченні та дослідженні властивостей стрічки Мебіуса та інших топологічних об`єктів.
- Збираючи матеріали та проводячи експерименти зі стрічкою Мебіуса, ми значно розширили свої знання з топології, побачили незвичайні властивості цієї фігури.
- Отже, наша робота - це спроба не тільки розглянути топологічну фігуру, а й показати доцільність і важливість її використання.
- З`ясувавши основні аспекти топології, виконавши власні досліди зі стрічкою Мебіуса, ми дійшли висновку, що безумовно є перспектива дослідження цієї фігури і спектр її використання досить широкий.
- Тема, яку ми обрали для дослідження, дала можливість заглибитись в надра науки математики, осягнути її велич і красу, широту застосування математичних знань.
- Вважаю, що матеріал наукової роботи буде корисним і цікавим як для учнів старших класів так і для вчителів математики, а також може використовуватись ними на факультативних заняттях та при вивченні топології студентами технічних вищих навчальних закладів.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Енциклопедія "Я пізнаю світ ": «Ранок» 2014р.
- Ерохин М. А. Исследование листа Мёбиуса с точки зрения математики // Молодой ученый. — 2014. — №4. — С. 6-12.
- Дж.Франсис, Книжка с картинками по топологии, М., Наука, 1991р.
- Фукс Д. «Лента Мёбиуса. Вариации на старую тему» : «Наука» 1978 р., с. 43 - 48.
- Науково-популярний журнал "Квант" 1975году № 7, 1977 № 7.
- .https://uk.wikipedia.org/wiki/
- https://www.lektorium.tv/course/27206
- w.w.w.Rambler.ru
Відгук
на науково-дослідницьку роботу « Стрічка Мебіуса та її незвичайні властивості » учня 11-А класу Полтавської загальноосвітньої школи І-ІІІ ступенів № 34 Левковського Романа Юрійовича
У роботі дано всебічний аналіз поняття топології як розділу математики, з’ясовано, що стрічка Мебіуса є однією з топологічних фігур, що мають тільки одну поверхню. Дослідження базуються на результатах опрацьованих джерел. Для відтворення історичного контексту розвитку поняття наведено історичні, теоретичні відомості. Для дослідження використано такі наукові методи, як аналіз, порівняння і синтез. У роботі детально проаналізовано властивості стрічки Мебіуса та її застосування в математиці, фізиці та інших науках, природі, техніці , архітектурі. Дослідження проілюстровано репродукціями, фотографіями, схемами, витягами з публікацій.
Очевидно, що учень цікавиться математикою, прагне розширити свої знання з даного предмету. Оригінальним є його власне дослідження властивостей загадкової стрічки Мебіуса.
Звичайно, в зазначеній темі існує перспектива дослідження інших властивостей цієї фігури та їх можливого застосування.
Учень виявив вміння ретельно працювати з літературними джерелами з теми дослідження, критично їх оцінювати та узагальнювати, користуватися сучасними методами дослідження; проявив організованість, самостійність, творчий підхід та ініціативність під час підготовки дослідження. Висновки сформульовано чітко й конкретно, вони випливають зі змісту роботи, підкріплені експериментальними матеріалами. Робота написана доступно, на досить високому науковому рівні.
На підставі зазначеного вище вважаємо, що дана робота має наукове і практичне значення, відповідає вимогам до оформлення науково-дослідницьких робіт. Розглянуті в роботі питання підтверджують актуальність і практичну значимість обраної теми. Цінним є ґрунтовність та всебічність дослідження, що дозволило зробити висновки про те, що матеріали дослідження можна використати для більш детального вивчення теми « Стрічка Мебіуса та її незвичайні властивості »


про публікацію авторської розробки
Додати розробку