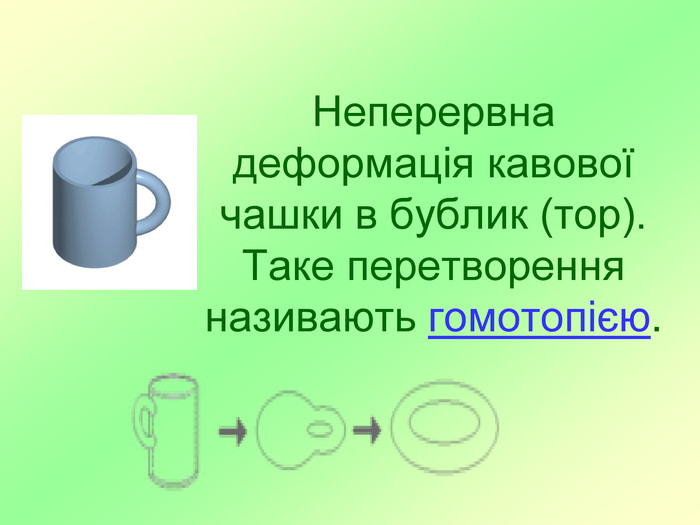
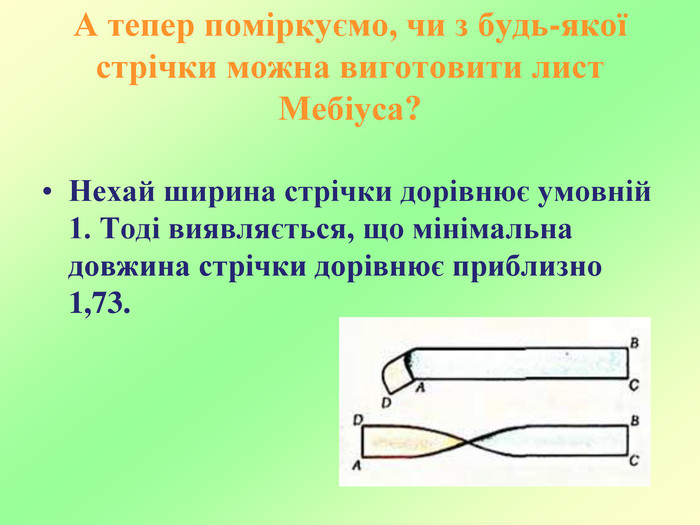
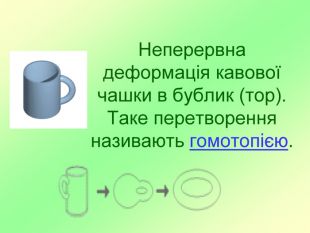
Презентація до наукової роботи " Стрічка Мебіуса"
Про матеріал
Презентація містить багато ілюстрацій, які висвітлюють практичне застосування стрічки Мебіуса, шлях її відкриття( історичний аспект), і навіть її місце у мистецтві. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку