Наукова робота "Звичайні дроби"

ЗМІСТ

ВСТУП

РОЗДІЛ I. Історія розвитку звичайних дробів

1.1. Поява звичайних дробів.

1.2 Дроби в стародавньому Єгипті.

1.3. Дроби в стародавньому Римі.

1.4. Дроби в Вавилоні

1.5 Нумерація і дроби в стародавній Греції

1.6. Дроби в інших державах давнини

1.8. Порівняння звичайних дробів

РОЗДІЛ IІ. Старовинні завдання з використанням звичайних дробів

РОЗДІЛ IІІ. Завдання з практичним змістом

РОЗДІЛ ІV. Застосування дробів у повсякденному житті

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ТЕЗИ

 науково-дослідницької роботи «Звичайні дроби»

Автор: Мироненко Юлія Олександрівна, учениця 9  класу Лубенської загальноосвітньої школи 

І-ІІІ ступенів №3 Лубенської районної ради Полтавської області

 

Науковий керівник: Гулак Тетяна Леонідівна, вчитель математики Лубенської загальноосвітньої школи  І-ІІІ ступенів №3

 

Мета дослідження: сформувати уявлення про виникнення і розвиток звичайних дробів; викликати інтерес до вивчення математики.

Для досягнення цієї мети були сформульовані завдання:

1) розвивати вміння працювати з додатковою літературою;

2) розглянути приклади застосування дробів в повсякденному житті;

3) прищепити інтересу до вивчення математики через розгляд історичних фактів;

4) навчитися узагальнювати отриману інформацію.

Структура роботи: робота складається із вступу, чотирьох розділів, висновків, списку використаних джерел та додатків.

Основними результатами роботи є:

• відшукання старовинних завдань з використанням звичайних дробів;
• розв’язання даних завдань за допомогою властивостей звичайних дробів;
• відшукання завдань із застосуванням звичайних дробі у повсякденному житті.

Гіпотеза: повсякденне життя людини не обходиться без дробів.

 

 

ВСТУП

На уроках математики при вивченні теми «Звичайні дроби» ми дізналися деякі історичні факти з появи і розвитку дробів. Мені захотілося розглянути це питання більш ґрунтовно: розглянути більш детально етапи розвитку звичайних дробів; знайти завдання з дробом, складені в далекому минулому. Хотілося в ході дослідження цього питання переконатися і переконати інших у необхідності дробів у повсякденному житті.

Актуальність і значимість моєї роботи бачу в тому, що буде цікавою для учнів і корисною для вчителів математики в якості додаткового матеріалу при проведенні уроків і заходів.

Мета дослідження: сформувати уявлення про виникнення і розвиток звичайних дробів; викликати інтерес до вивчення математики.

Дана мета може бути реалізована шляхом розв’язання наступних завдань, а саме:

• розвивати вміння працювати з додатковою літературою;
• розглянути приклади застосування дробів в повсякденному житті;
• прищепити інтересу до вивчення математики через розгляд історичних фактів;
• навчитися узагальнювати отриману інформацію.

Об’єкт дослідження – події, які розгорталися навколо звичайних дробів.

Предмет дослідження – звичайні дроби.

Наукова новизна полягає в систематизації різних матеріалів про звичайні дроби: історичних, математичних, інформаційних.

Практичне знання дослідження – у можливості застосування його для популяризації математичних знань, для розвитку мислення, для міжпредметних зв’язків.

Особистий внесок полягає в пошуці завдань, а також у самостійному розв’язанні старовинних задач з використанням звичайних дробів.

 

 

РОЗДІЛ I. Історія розвитку звичайних дробів

1.1. Поява звичайних дробів.

Що може бути простіше рахунку? Говорити поспіль: один, два, три, чотири, п'ять і т.д. зможе кожний. Рахунок увійшов в наш побут так міцно, ми з ним так зжилися, що не можемо собі уявити людину, яка не вміє рахувати. І все ж був час, коли люди рахувати не вміли. Наші віддалені предки, що населяли землю тисячі століть тому, які не знали вогню, не знали і рахунку.

У старовинних переказах згадуються пророки і герої, яким боги відкрили або які самі забрали у богів вогонь і число. Таких пророків і героїв, зрозуміло, ніколи не було. Люди навчилися рахувати самі, поступово протягом сотень століть, передаючи свій досвід і свої знання з покоління в покоління, розвиваючи та вдосконалюючи мистецтво рахунку.

На древніх гробницях, на руїнах старих храмів знаходять іноді дивні позначення. Вченим вдалося їх прочитати і дізналися, як жили люди чотири-п'ять тисяч років тому. З цих написів видно, що і тоді наші предки рахували непогано. Але як вважали вони ще раніше, коли не вміли писати? Про це ми можемо тільки здогадуватися.

У ті віддалені часи, коли люди ледь навчилися говорити і користуватися вогнем, вони знали тільки два числа: один і два. Число «два» пов'язувалося з органами зору і слуху та взагалі з конкретною парою предметів. Якщо перерахованих предметів було більше двох, то люди говорили просто «багато». «Багато» було зірок на небі, але і пальців на руці було теж «багато».

Поступово до перших двох чисел додавалися нові і нові. Люди навчилися рахувати до п'яти і з'єднувати дві «п'яти» в десяток. На перших щаблях розвитку суспільства люди рахували за допомогою десяти пальців рук. По сьогодні існує вислів «Перерахувати на пальцях». Так поступово збільшувався набір чисел, які вживали при рахунку предметів, тобто з'явилися натуральні числа.

В житті людині доводилося не тільки рахувати предмети, а й вимірювати величини. Люди зустрілися з вимірами довжин, площ земельних ділянок, обсягів, маси тіл. Наприклад, вимірюючи довжину ділянки кроками, людина зустрічалась з таким явищем: довжина складалася з десять кроків, і залишався залишок менше одного кроку. Поява дробів пов'язано у багатьох народів з розподілом добичі на полюванні. У зв'язку з цією необхідною роботою люди стали вживати вирази: половина, третина, два з половиною кроку. Звідки можна було зробити висновок, що дробові числа виникли як результат вимірювання величин.

1.2 Дроби в стародавньому Єгипті.

Перший дріб, з яким познайомилися люди, був, напевно, половина. За ним послідували   ..., потім і т.д., тобто найпростіші дроби, частки цілого, звані одиничними або основними дробами. У них чисельник завжди одиниця. Єгиптяни виражали будь-який дріб у вигляді суми тільки основних дробів. Наприклад, ;  ;

У стародавньому Єгипті архітектура досягла високого розвитку. Про це свідчать збережені до наших днів єгипетські піраміди. Зрозуміло, для того щоб будувати їх, щоб обчислити довжини, площі і обсяги фігур, необхідно було знати арифметику.

Єгиптяни писали на папірусі, тобто на свитках, виготовлених з стебла великих тропічних рослин, які мали таку ж назву.

Найважливішим за змістом є «папірус Ахмеса», по імені одного з найдавніших переписувачів, рукою якого він був написаний. Його довжина 544см, а ширина 33 см; зберігається він у Лондоні, в Британському музеї. Цей старовинний математичний документ має таку назву: «Способи, за допомогою яких можна дійти до розуміння всіх темних речей, всіх таємниць, які полягають в речах». У цьому папірусі є таблиці для представлення деяких дробів у вигляді суми одиничних дробів. [Додаток А]

1.3. Дроби в стародавньому Римі.

Римляни користувалися, в основному, тільки конкретними дробами, які заміняли частини відомих величин. Повільним і тривалим був перехід від конкретних до абстрактних дробів, не пов'язаними з певними мірами. Вони зупинили свою увагу на міру «ас», яка у римлян служила основною одиницею вимірювання маси, а також грошовою одиницею. Ас ділився на дванадцять частин - унцій. З них складали всі дроби зі знаменником 12, тобто і т. д.

Так виникли римські дванадцяткові дроби, тобто дроби, у яких знаменником завжди було число 12. Замість римляни говорили «одна унція»,  - «п'ять унцій» і т.д. Три унції називалися чвертю, чотири унції – третиною, шість унцій – половиною.

Для дробів, знаменник яких отримували шляхом ділення частки на більш дрібні, були особливі назви. Навіть зараз іноді кажуть: «Він скрупульозно вивчив це питання». Це означає, що питання вивчене до кінця, що жодної найменшої неясності не залишилося. А слово «скрупульозно» від римської назви аса - «скрупулус». Користувались і такими назвами: «семіс» - половина аса, «секстане» - шоста його частка, «семіунція» – полунця і т.д.

Щоб працювати з дробом, треба було пам'ятати для цих дробів і таблицю додавання, і таблицю множення. Для полегшення роботи складалися спеціальні таблиці, деякі з них дійшли до нас.      

Зараз «ас» – аптечний фунт.

1.4. Дроби в Вавилоні

Близько 4 тисяч років тому в Месопотамії – долину між Тигром і Ефратом на території нинішнього Іраку – прийшли два кочових населення: сумерійці і акадяни. Через два століття вони злилися в одну потужну державу – Вавилон.

На час злиття кожен з цих народів мав свої вагові та грошові одиниці. Основною одиницею у сумерійців була «міна», а у акадян - «шекель». «Шекель» була приблизно в 60 разів менше «міни». Наступній ваговій одиницею встановили «талант», вона була в 60 разів більше «міни».

Походження шістдесяткової системи обчислення у вавилонян пов'язано, як вважають вчені, з тим, що вавилонська грошова і вагова одиниця виміру поділялися в силу історичних умов на 60 рівних частин: 1 талант = 60 мін; 1 міна = 60 шекель.

У стародавньому Вавилоні високий рівень культури був досягнутий ще в третьому тисячолітті до н.е. там писали не на папірусі, а на глині. Шляхом натиску клиноподібної палички на м'які глиняні плитки наносилися рисочки, що мали вигляд клинів. Ось чому такий лист називався клинописом. Плитки сушилися на спекотному сонці і набували міцність. Виходили міцні цегляні «документи»; деякі з них збереглися і до нашого часу. Вчені знайшли при розкопках чимало цегляних актів, державних і торгівельних договорів, навіть підручників. Розкопками, проведеними в ХХ столітті серед руїн древніх міст південної частини Дворіччя, виявлено велику кількість клинописних математичних табличок. Вчені, вивчаючи їх, встановили, що за 2000 років до н. е. у вавилонян математика досягла високого рівня розвитку. [Додаток Б]

Письмова шістдесяткова нумерація вавилонян комбінувалася їх двох значків: вертикального клина ▼, так позначали одиницю, і кутового знака ◄, так позначали десять. У вавилонських клинописних текстах вперше зустрічається позиційна система числення. Вертикальний клин позначав не тільки 1, але і 60, , 60³ і т.д. Знака для нуля в позиційній шістдесятковій системі у вавилонян спочатку не було. Пізніше був введений знак, який замінює сучасний нуль, для відділення розрядів між собою.

Шістдесяті частки були звичні в житті вавилонян, вони записували всі  дроби зі знаменником 60 або його степеня.

Наприклад, запис у вавилонян 4; 52; 03 означає .

Сліди вавилонської шістдесяткової системи числення використовуються і в сучасній науці при вимірі часу і кутів. До наших днів збереглося розподіл години на 60 хвилин, хвилини на 60 секунд; кола на 360 градусів, градус на 60 хвилин, а хвилини на 60 секунд.

Вавилоняни внесли цінний внесок в розвиток астрономії. Шістдесятковими дробами користувалися в астрономії вчені всіх народів до XVII століття, називаючи їх астрономічними дробами. На відміну від них, дроби загального вигляду, якими користуємося ми, були названі звичайними.

1.5 Нумерація і дроби в стародавній Греції

У Стародавній Греції існували дві системи письмової нумерації: аттична і іонійська або алфавітна. Вони були так названі по давньогрецьким областям - Аттика й Іонія. В аттичній системі, названою також геродіановою, більшість числових знаків є першими буквами грецьких відповідних числівників, наприклад, ГЕNTE (генте або пенте) - п'ять, ΔЕКА (дека) - десять і т.д. Цю систему застосовували в Аттиці до I століття н.е., але в інших областях Стародавньої Греції вона була ще раніше замінена більш зручною алфавітної нумерацією, яка швидко поширилася по всій Греції.

У грецьких творах з математики дробів не зустрічалося. Грецькі вчені вважали, що математика повинна займатися тільки цілими числами. Возитися з дробом вони надавали купцям, ремісникам, а також астрономам, землемірам і іншим «чорним людям». У Стародавній Греції арифметику – вчення про загальні властивості чисел – відокремлювали від логістики – мистецтва обчислення. Греки вважали, що дроби можна використовувати тільки в логістиці. Тут ми вперше зустрічаємося із загальним поняттям дробу виду . Таким чином, можна вважати, що вперше область натуральних чисел розширилася до області додаткових раціональних чисел в Стародавній Греції не пізніше V століття до н. е. Греки вільно оперували всіма арифметичними діями з дробами, але числами їх не визнавали.

Греки вживали поряд з одиничними, «єгипетськими» дробами і загальні звичайні дроби. Серед різних записів вживалася і така: зверху знаменник, під ним – чисельник дробу. Наприклад, означало три п'ятих і т.д.

1.6. Дроби в інших державах давнини

Близько в II ст.н.е. в китайському трактаті «Математика в дев'яти книгах» вже мають місце скорочення дробів і всі дії з дробами. Ця книга була призначена для землемірів, техніків і рахункових працівників.

Індія, одна з найдавніших і величних країн світу, є батьківщиною позиційної десяткової нумерації (V-VII ст.н.е.).

Індійці широко вживали «звичайні» дробу. Наше позначення звичайних дробів за допомогою чисельника і знаменника було прийнято в Індії ще в VIII ст.н.е., проте запис був без дробової риски. Дробову риску стала застосовувати лише в XIII столітті.

Широко відомі математики давньої Індії Аріабхатта (V ст.), Брахмагупта (VII ст.), який виклав правила дії з дробами, мало відрізнялися від наших, і Бхаскара (X ст.). У них зустрічаються різні дроби: і основні, і довільні з будь-яким чисельником. Чисельник і знаменник записуються так само, як і у нас зараз, але без горизонтальної риски, а просто розміщуються один над іншим. Близько 1500 років тому індуси першими почали відокремлювати рискою чисельник від знаменника.

У VII ст.н.е. жив відомий вірменський вчений Ананій Ширакаці, він писав книги з математики, географії та астрономії. Він склав величезні таблиці додавання, віднімання і множення чисел. Серед книг Ананія є також арифметика і збірник задач, названий «Питання і відповіді». 1300 років тому Ананій розв’язував завдання з дробами, які навіть для багатьох вчених з Європи на той час здавалися важкими.

Леонардо Пізанський вже записує дроби, поміщаючи в разі змішаного числа, ціле число праворуч, але читає так, як прийнято у нас.

Йордан Неморарій (XIII ст.) виконує розподіл дробів за допомогою розподілу чисельника на чисельник і знаменник на знаменник, уподібнюючи ділення множенню. Для цього доводиться, члени першого дробу доповнювати множниками:

У XV - XVI століттях вчення про дроби набуває вже знайомий нам тепер вид і оформлюється приблизно в ті самі розділи, які зустрічаються в наших підручниках.

Слід зазначити, що розділ арифметики про дроби довгий час був одним з найбільш важких. Недарма у німців збереглася приказка: «Потрапити в дроби», що означало – зайти в безвихідне становище. Вважалося, що той, хто не знає дробів, не знає і арифметики.

В ході розвитку математики було помічено, що найзручнішими для обчислення є десяткові дроби. З XVII - XVIII ст. вони отримали загальне поширення, особливо після створення і введення в більшості країн метричної системи заходів.

1.8. Порівняння звичайних дробів

При порівнянні дробів з однаковими знаменниками ділили щось ціле на задану кількість частин і порівнювали потрібну кількість частин першого та другого дробів. Що більше або ? Ділимо пиріг на 5 рівних частин і бачимо, що дві таких частини менше трьох таких же частин.

При порівнянні дробів з однаковими чисельника міркували так: чим на більшу кількість частин ділимо одне і теж число, тим менший виходить дріб.

Але порівнювати доводилося і інші дроби, які не підходять під ці правила. Порівнювати дроби, використовуючи прийом зведення дробів до спільного знаменника, люди навчилися набагато пізніше, а до цього вони користувалися багатьма іншими способами, які приводили їх до вірного результату.

1 спосіб: порівняння з половиною.

Що більше або ? Якщо ці дроби порівнювати з , то менше , а більше . Це означає, що більше .

2 спосіб: порівняння шляхом додавання до одиниці.

Візьмемо дроби і . Перший дріб доповнюємо до одиниці дробом , а другий - . Але при порівнянні дробів з однаковими чисельника отримуємо, що менше , це означає, що більше .

3 спосіб: порівняння правильних і неправильних дробів: будь-який правильний дріб менший за неправильний.

РОЗДІЛ IІ. Старовинні завдання з використанням звичайних дробів

У різних посібниках я знайшла цікаві завдання, які були використані в різні історичні періоди.

1. Завдання Ейлера.

Леонард Ейлер (4 квітня 1707г.- 18 вересня 1783р.)  – є засновником російської наукової математичної школи. Повне зібрання його творів налічує понад 70 томів, а списки його праць – понад 850 назв.  

Вирішивши всі свої заощадження поділити порівну між усіма синами, склав заповіт. «Старший з моїх синів повинен отримати 1000 рублів і восьму частину залишку; наступний – 2000 рублів і восьму частину нового залишку; третій син – 3000 рублів і восьму частину наступного залишку і т.д. »

Визначте число синів і розмір заповіданого заощадження.

Розв’язання: оскільки всі сини отримали порівну, то восьма частина кожного нового залишку була на 1000 рублів менше восьмої частини попереднього залишку, а, значить, весь новий залишок був на 8000 рублів менший попереднього. Оскільки за умовою всі гроші були поділені повністю, то, коли молодший син отримав за заповітом, крім кількох тисяч рублів, ще восьму частину залишку, цього залишку не виявилося. Але тоді попередній залишок 8000 рублів. З нього передостанній син отримав восьму частину, рівну 1000 рублів, а решта 7000 рублів отримав молодший син, який, таким чином, був сьомим сином: синів було сім, а заповідана сума 49000 рублів.

2.     Цю задачу більш 200 років тому задавав своїм учням учитель математики Йоганн Хемелінг.

Від числа одну восьму

Взявши, додай ти до неї будь-яку

Половину від трьохста,

І вісьмірка перевершить

Чи не трохи – на п'ятдесят

Три четвертих. Буду радий,

Якщо той, хто знає рахунок,

Мені число те назве.

Рішення: той, хто знає рахунок, складе рівняння                    

3.               Історія зберегла нам мало рис біографії чудового стародавнього математика Діофанта. Все, що відомо про нього, почерпнуто з напису на його гробниці – напису, складеної в формі математичної задачі.

Подорожній! Тут прах був похований Діофанта. І числа розповісти можуть, про диво, як довгий був вік його життя.

Частину шосту його представляло прекрасне дитинство.

Дванадцята частина життя протекла  – покрилось пухом тоді  і підборіддя. Сьому в бездітному шлюбі провів Діофант.

Минуло п'ятиріччя; він був ощасливлений народженням прекрасного сина первістка.

Якому доля половину лише життя прекрасної і світлої дала на землі в порівнянні з батьком.

І в печалі глибокої старець земного спадку кінець сприйняв, переживши чотири роки з тих пір, як сина позбувся.

Скажи, скільки років життя досягнувши, смерть прийняв Діофант?

Розв’язання: прийнявши все життя Діофанта за х, можна скласти рівняння        

Це означає, він одружився в 21 рік, став батьком на 38 році, втратив сина на 80-му році і помер в 84 роки.

4.     Відомий фізик А.В. Цингер в своїх спогадах про Л.Н. Товстого розповідає в наступній задачі, яка дуже подобалася відомому письменнику:          

«Артілі косарів треба було скосити два луги, один вдвічі більший іншого. Половину дня артіль косила великий луг. Після цього артіль розділилася навпіл: перша половина залишилася на великій галявині і докосили його до кінця вечора; друга ж половина косила малий луг, на якому до вечора ще залишилася ділянка, яка була скошена косарем на інший день за один день роботи. Скільки косарів було в артілі? »

Розв’язання: якщо великий луг півдня косила вся артіль і півдня пів артілі, то за пів дня пів артілі скошує лука. Отже, на малому лузі залишилася нескошена ділянка . Якщо один косар скошує в день лука, а скошено було , то косарів було вісім.

5.     Завдання зі збірки «Питання і відповіді» вірменського вченого Ананія Ширакаці.      

Один купець пройшов через 3 міста, і стягували з нього в першому місті мита половину і третину майна, і в другому місті половину і третину майна, що залишилося, і в третьому місті половину і третину майна, що залишилося. І коли він прибув додому, у нього залишилося 11 грошиків.

Дізнайся, скільки всього грошиків було спочатку у купця.      

Рішення: приймаємо все майно купця за х, в кожному місті він віддавав свого майна. Це означає, що в першому місті він віддав х, і у нього залишилося х.

У другому місті він віддав свого майна, і у нього залишилося, і у нього залишилося  

Аналогічно обчислюється залишок майна після проходження третього міста І цей залишок дорівнює 11, отже . У купця було 2376 грошиків.

6.     У місті Афінах була водойма, в який проведено три труби. Перша могла наповнити водойму за 1 годину, друга – за 2 години, а третя – за 3 години. Дізнайся, за який час всі 3 труби разом наповнили водойму.

Розв’язання: перша труба за одну годину заповнює всю водойму, що дорівнює х, а друга труба за одну годину заповнює половину водойми, тобто , а третя - . Знайдемо час заповнення водойми трьома трубами

За годин три труби заповнять водойму.

7)  Задача знаменитого індійського математика XII століття Бхаскари.

Є кадамба-квітка; на одну пелюстку бджілок п'ята частина сіла. Поряд росла вся у цвіту семиндга, і на ній третя частина розмістилася. Різницю їхню ти знайди, тричі її ти додай, на кумай цих бджіл посади. Лише бджілка одна не знайшла собі місця ніде, усе літала туди-сюди та скрізь пахощами квітів тішилася. Тепер скажи мені: скільки бджілок усього тут зібралося?

Розв’язання: Нехай усього зібралося х бджілок. Складаємо рівняння:

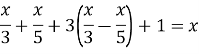
Отже, всього зібралося 15 бджілок. 

РОЗДІЛ IІІ. Завдання з практичним змістом

1. З метою пожежної безпеки агрегати з приготування трав'яного борошна повинні знаходитися на відстані не менше 30 м від скирт соломи, ємності з пальним – не менше ніж на цієї відстані, тваринницькі приміщення – не менше ніж на останньої відстані. Визначте ці відстані.

2. Вирощування бичків складається з трьох періодів: це молочний, дорощування і заключний відгодовування. До кінця першого періоду бичок досягає маси 120кг, що становить маси бичка, що досягається до кінця другого періоду, маса в кінці другого періоду становить маси бичка, що досягається до кінця третього періоду. Визначте масу бичка, що досягається до кінця третього періоду.

3. Перше підгортання картоплі проводиться тоді, коли бадилля досягає висоти дм, при цьому підгортання проводиться на висоти гички. Визначте висоту першого підгортання картоплі.

4. Житловий будинок повинен розташовуватися на відстані не менше 6 м від проїжджої частини вулиці. Приміщення для тварин повинні знаходитися від будинку в рази. А сміттєві контейнери в рази далі, ніж будинок від проїжджої частини вулиці. Визначте ці відстані.

5. При вибухових роботах на відкритій місцевості підривники для безпеки повинні відійти від місця вибуху на 300м, при корчування пнів – не менше ніж на цієї відстані, а при дробленні валунів зарядами повинні відійти на відстань, в рази більше, ніж при корчування пнів. Визначте безпечну відстань при цих вибухових роботах.

6. Мінімальна температура для проростання насіння огірка 15⁰, у кукурудзи , а у буряка температури проростання насіння огірка. Визначте мінімальну температуру проростання насіння кукурудзи та буряка.

7. Комплекс з виробництва свинини має 5200 га посівних площ. З них 65% займають зернові культури, залишку – кормові культури, а решта площі зайнята картоплею. Визначте цю площу.

8. Від однієї корови в рік було отримано 5000кг молока при жирності 3,7%, а від іншої 4600 кг при жирності 4,5%. У молоці якої корови і на скільки більше містилося молочного жиру?

9. При розпилюванні колоди на дошки його об’єму перетворюється в тирсу, а при обробці дощок ще об’єму колоди йде в стружку. Яка частина об’єму колоди йде в стружку?

10. всіх витрат підприємства становили витрати на сировину, на заробітну плату і на паливо і освітлення. Яку частину всіх витрат підприємства становили ці витрати?           

11. Як, не маючи ніяких вимірювальних засобів, відміряти 50 см від шнурка, довжина якого 2/3 метра?         

12. Господиня спекла для гостей пиріг. До неї може прийти або 10, або 11 чоловік. На яку найменшу кількість шматків їй потрібно заздалегідь розрізати пиріг так, щоб його можна було поділити порівну як між 10, так і між 11 гостями?          

13. Як розділити 7 яблук між 12 хлопчиками, якщо ні одне яблуко не можна різати більш ніж на п'ять частин?        

14. У класі навчається менше 50 школярів. За контрольну роботу сьома частина учнів отримала п'ятірки, третя – четвірки, половина – трійки. Решта робіт були оцінені як незадовільні. Скільки було таких робіт?           

15. Петя витрачає свого часу на гру у футбол, - на навчання в школі, - на перегляд кінофільмів, - на розв'язання олімпіадних завдань, і - на сон. Чи можна так жити?           

16. Ощадбанк нараховує вкладнику 12% річних. Вкладник поклав на рахунок 30 000 грн. і не знімав гроші з рахунку протягом трьох років і не брав процентні нарахування. Скільки гривень буде на рахунку вкладника через рік? Через три роки?          

17. Холодильник коштував 12 600 грн. У травні ціна холодильника була знижена на 20%, а в червні – ще на 5%. Яка стала вартість холодильника в червні?         

18. На початку року тариф на електроенергію становив 72 коп. за 1 кВт / год. В середині року він збільшився на 50%, а в кінці року ще на 40%. Як ви вважаєте, чи збільшився тариф на 90%? Менш ніж на 90%? Більш ніж на 90%?

РОЗДІЛ ІV. Застосування дробів у повсякденному житті

1.     Дроби і музика.      

Ноти відрізняються за тривалістю їх звучання. Знаком позначають цілу ноту, ноту вдвічі коротшу (половинну) - , четвертну - ,  восьму - , шістнадцяту - .

2.     Золотий переріз.      

Золотий переріз — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d.

Предмети, які нас оточують, також часто дають приклади золотого перерізу. Наприклад, палітурки багатьох книг мають відношення ширини і довжини, близьке до значення 0,618.       

Гарний витвір давньогрецької архітектури – Парфенон - побудовано в V ст. до н.е. відношення висоти будівлі до його довжини рівне 0,618. [Додаток В]

3.     Географія.

Ділянки земної поверхні зображуються на карті в зменшеному вигляді. Для цього використовується поняття масштабу: відношення довжини відрізка на карті до довжини відповідного відрізка на місцевості.

Наприклад: масштаб карти означає, що 1 см на карті відповідає 10000см на місцевості.

4.         Архітектура.

Звичайні дроби дуже широко застосовуються в будівництві та архітектурі. Одним з найважливіших методів побудови виразної і цілісної архітектурної форми є дотримання певних правил: співмірність, певне співвідношення частин архітектурної споруди між собою. [Додаток Г]

5. Людина і дроби тісно пов’язані між собою.

маси тіла людини становить кров;

  всієї крові міститься в кровоносних судинах;

  у печінці;

  у селезінці;

  у підшкірних судинах;

л крові виштовхується за одне скорочення серця;

6.  Земля і дроби.

– покрито водою

– суша

– поверхня Землі на якій можна жити

-  пустелі, гори, ліси,

– місця , де можуть жити люди

– поля, де вирощують врожай.

Уявіть собі, що яблуко – це наша Земля . Розріжте його на частинки і ви побачите, яка мала частина Землі  придатна для життя  людини.

7. Ігри.  

Починаючи знайомити дитину з грою, використовуйте ті завдання, які враховують вік і рівень її розвитку.

• Дістаньте ціле коло і задайте  питання: "На що це схоже?" (Наприклад: коло - на яблуко, пиріг, м'яч і т.д.). Потім покажіть друге коло, що складається з двох половинок. Чим відрізняються кола? Скільки частин у другому колі? Чи однакові кола?

• Гра "Магазин": дитина в ролі продавця, дорослий – покупець, кола – це фрукти. Дорослий просить: "Дай мені, будь ласка, ціле яблуко, половинку яблука, одну другу яблука". Потім міняються ролями. Гра стане більш цікавою, якщо додати кола, розділені на 3,4,5 частин і т.д.

• Запропонуйте дитині обвести ціле коло і "перетворити" його в сонечко, кавун, колесо, використовуючи папір і кольорові олівці. Половинку кола – в гриб, парасольку і т.д.

• У грі можна використовувати вірші-загадки.

• Можна створити ситуацію, при якій виникає необхідність розділити предмет на дві рівні частини (допомогти двом мишкам розділити сир).

• Розділити 1-2 кола на дві і більше частини. Перевірити накладенням чи рівні отримали  частини, порахувати їх і, з'єднавши разом, знову отримати цілий круг. Обвести контури цілого кола і його частини. Порівняти розміри цілого кола і частини, 1 = = . Скільки частин у кожному колі?

• Взяти 3 кола. Один цілий, другий розділити на дві частини, третій - на чотири частини. Порівняти розмір однієї другої і однієї четвертої частини і їх кількість. Питання які можна задати дитині: що більше - половинка або ціле коло?  що менше - ціле коло або половинка?  що більше - половинка або одна з чотирьох частин (одна чверть)? Чому?

Висновок. Чим на більшу кількість частин ділиться предмет, тим менше ці частини.

• Скільки разів треба скласти коло, щоб розділити його на дві (чотири) рівні частини? Якщо коло скласти один (два, три ...) рази навпіл, скільки частин отримаємо? Тут можна використовувати також кола, попередньо вирізані з паперу.

• Показати одну частину круга (одну третину, одну четверту та ін.). Нехай дитина спробує здогадатися, скільки частин було в колі?

ВИСНОВКИ

Крім нуля і натуральних

Є ще числа "незвичайні"!

Половина і третина,

Чверть години, півхлібини -

Все, що ділимо щоднини

На рівнесенькі частини

Записати маєм спробу,

Тут нам допоможуть дроби.

 

В результаті роботи над дослідженням ми дізналися історію розвитку звичайних дробів, зуміли розглянути завдання давнини, пов'язані з дробом і завдання з практичним змістом. В ході їх вирішення, закріпили алгоритми виконання дій над дробами, знаходження числа від його частини і частини від числа.      

Особливий інтерес при роботі над дослідженням ми випробували при розв’язанні старовинних завдань з використанням дробів.      

Різноманітність запропонованих завдань переконали нас в необхідності застосування дробів в повсякденному житті і для багатьох професій.      

Вважаємо, що матеріали моєї роботи будуть цікавими для інших учнів. Вони можуть бути використані як на уроці, так і для проведення позакласних заходів з математики.

Хотілося б продовжити роботу по знаходженню застосування дробів в різних професіях і в життєвих ситуаціях.

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Григорьева Г.И. Математика. Предметная неделя в школе. – М.: Глобус, 2008г.
2. Захарійченко Ю. О., Школьний О. В., Захарійченко Л. І., Школьна О. В. Поний курс математики в тестах – Х.: Вид-тво «Ранок», 2015.
3. Каплун О. І. математика. Навчально-практичний довідник – Х.: ТОРСІНГ ПЛЮС, 2012.
4. Міжнародний математичний конкурс «Кенгуру – 2007». Інформаційний вісник. – Львів: Каменяр, 2007. – 47 с.
5. Міжнародний математичний конкурс « Кенгуру – 2008». Інформаційний вісник. – Львів: Каменяр, 2008. – 52 с. 13.
6. Міжнародний математичний конкурс « Кенгуру – 2009». Інформаційний вісник. – Львів: Каменяр, 2009. – 56 с.
7. Сарана О. А. Математичні олімпіади: просте і складне поруч/О.А. Сарана. – К.: « А.С. К.», 2004. – 344 с.
8. Федак І. В. Готуємося до олімпіади з математики/І.В. Федак. – Кам'янець – Поділ.: Абетка, 2006. – 420 с.
9. Якишеляк В. Й. Цікава математика.// Математика. – 2002.- № 17.

 

ІНТЕРНЕТ-РЕСУРСИ

• Використання дробів у повсякденному житті [Електронний ресурс] http://tatyana2112.blogspot.com
• Історія виникнення дробів [Електронний ресурс] http://bloguchnivistoriki.blogspot.com

Додаток А

Частина папіруса Ахмеса

Додаток Б

Вавилонські таблички

Додаток В

Парфенон у Греції

Додаток Г

Спасо-Преображенський Мгарський монастир