Науково-дослідна робота "Математика в мистецтві"

Експериментальний загальноосвітній

навчальний заклад Всеукраїнського рівня

Міністерство освіти і науки України

«Навчально-виховний комплекс: загальноосвітня

школа І-ІІ ступенів – ліцей №7

Вінницької міської ради»

 

 

 

 

 

ПРОГРАМА

 «Колективний

науковий

проект»

 

 

 

 

Науково-дослідницька робота

 

 

 

 

Вінниця 2019

Математика в мистецтві

Проект 11-ЕК класу закладу «НВК:ЗШ І-ІІ ст. – ліцей №7 ВМР»

 

Куратор: Сороколіта Ірина Миколаївна, учитель математики та фізики, учитель вищої категорії, старший вчитель

 

Науковий консультант: Бондар Марина Валеріївна, кандидат наук, доцент кафедри економічної кібернетики та інформаційних систем ВТЕІ КНТЕУ

 

Актуальність теми. Вся сучасна наука: фізика, хімія, економіка тощо не лише використовує математичні методи, а й будується за математичними законами. Шлях в сучасну науку й техніку, просто в сучасне життя пролягає крізь математику. Справа полягає не тільки в тому, що людина в сучасному світі має орієнтуватися у кількісних і просторових співвідношеннях, виконувати елементарні арифметичні обчислення, а, й у тому, що вивчення насамперед математики формує культуру логічного мислення, яка потрібна і тим, хто планує повязати себе у майбутньому з гуманітарною та творчою діяльністю.

 

Мета роботи. З’ясувати, чи може мистецтво існувати без математики, чи існує зв'язок між математикою та музикою, літературою, образотворчим мистецтвом, архітектурою, живописом. Через ряд заходів показати учням закладу, що математика присутня навіть в художній  літературі. Дослідити як математика впливає на здібності учнів до музики та образотворчого мистецтва. Показати важливість рівня знань з математики при вступі до ВНЗ.

 

В ході роботи над проектом ми провели опитування ліцеїстів спеціальності «комп’ютерний дизайн». З метою підвищення інтересу до вивчення математики, провели позакласний захід для учнів 6-х класів. Здійснили порівняльний аналіз якості знань з математики учнів, які займаються музикою, з тими , які музикою не займаються. Зробили підбірку ВНЗ для учнів, які у майбутньому планують повязати себе з архітектурою. Відкрили для себе новинку у мистецтві – теорію фракталів. Для кафедри учителів математики зібрали серію мультфільмів та художніх фільмів, які пов’язані з математикою, а також ряд презентацій , що стануть в пригоді учителям, які викладають математику в класах комп’ютерного дизайну.

 

ЗМІСТ

ЗМІСТ……………………………………………………………………………...3

ВСТУП…………………………………………………………………………….4

РОЗДІЛ І. Магія математики в мистецтві……………………………………....6

1.1. Математика і живопис………………………………………………..6

1.2. Математика в архітектурі………………………………………….....9

1.3. Математика і музика…………………………………………………12

1.4. Фрактал – математика мистецтва…………………………………...19

РОЗДІЛ ІІ. Математика і мистецтво – фундаменти освіти…………………...27

2.1. Математика та кіно…………………………………………………..27

2.2. Математичні вірші…………………………………………………...30

2.3. Математика в художніх творах……………………………………..32

2.4. Нумеризм Сієни Моріс………………………………………………36

2.5. Математика і спеціальність комп’ютерного дизайну……………...41

ВИСНОВОК……………………………………………………………………...45

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………………….46

ВСТУП

Світ, у якому ми живемо, прекрасний і гармонійний. Безперечно, у Творця бездоганний естетичний смак: від малюсінького павучка, що тче в траві свою павутину, до незлічимих галактик, загадкових зірок, планетних систем, що здійснюють свій шлях у безмежному просторі.

Світобудова, будь-який досліджуваний об’єкт, видимий предмет, явище можна, в принципі (чи буде коли-небудь можна!), описати мовою математики. Створюючи прилади, апарати різного призначення, ми давно вже звертаємося за підказками до природи. Вивчаючи (відкриваючи) для себе ці закони, ми пізнаємо світ, поступово вивчаємо його й розширюємо межі нашого пізнання. Тим часом розвивається математична наука, як один із наймогутніших засобів пізнання навколишнього світу.

Питання про роль математики в мистецтві хвилювало ще стародавніх греків (потрібно згадати школу піфагорійців). Слід зазначити , що свій інтерес греки успадкували від попередніх цивілізацій , так загострений інтерес Піфагора до математичної теорії музики був запозичений ним від давніх вавилонян. Більше того , можна припустити , що математика і мистецтво виникли майже одночасно. Їх походження було пов’язане з релігійно-філософськими пошуками людини , зі спробами якось «пояснити світ». Можливо, найдавніші пам’ятки мистецтва і математики належать кроманьйонцям (епоха давнього неоліту). Так звані петрогліфи (наскельні малюнки) в печерах Іспанії і південної Франції відрізняються прекрасними художніми якостями і неперевершеним відчуттям форми. Не виключено , що від цих часів веде свій початок властивий піфагорійцям погляд на математику і мистецтво , як на ті основи , які допомагають зрозуміти закони природи , розкрити гармонію і бездоганність Всесвіту , і цей , здавалося б примітивний погляд на світ , не такий уже й відмінний від наукового світосприйняття наших днів. І якщо математика і мистецтво з самого початку були пов’язані з релігією , то  потім вони виросли в основні інструменти всякого знання. Не випадково особливу увагу до мистецтва звертали

багато видатних учених , в тому числі деякі з найвизначніших математиків ХХ ст. Герман Бейль та Альберт Ейнштейн. З іншого боку, наявність математики в мистецтві зацікавила багатьох творців прекрасного, в тому числі таких гігантів, як Леонардо да Вінчі і Альбрехта Дюрера, які здійснили так звану «особисту унію» між математикою і мистецтвом.

Глибокий сенс має вислів «Шукайте мистецтво в математиці». Математика красива: естетичні критерії грають в ній дуже важливу роль. Кожний математик знає , що зовнішня непривабливість того чи іншого доказу сама по собі служить достатньою основою , щоб засумніватися в ній: частіше за все вона свідчить про незавершеність , про неповноту мислення , якщо не просто про його хибність. Навпаки , внутрішня досконалість та чіткість математичної побудови майже завжди гарантують його важливу істину.

 Ще здавна геометрія належала до семи вільних мистецтв , які входили до складу тривіума (граматика , риторика і діалектика) і квадривіума (арифметика , геометрія , астрономія , музика). Звичайно , сім вільних мистецтв з часом змінювалися. Так в епоху Відродження особливого розквіту набув квадривіум. Так арифметика і геометрія, доповнені алгеброю, перетворились в математику. Можна впевнено сказати, що геометрія до недавнього часу вважалась невід’ємною частиною загальної освіченості — освіченості , не пов’язаної з надбанням певної професії. Математика (особливо геометрія) несе великий історичний інтерес , практичне застосування і володіє внутрішньою красою.

РОЗДІЛ І

Магія математики в мистецтві

 

1.1.Математика і живопис

Геометричні мотиви нерідко присутні в картинах великих живописців. Хоча художник часто діє інтуїтивно, але мистецтвознавець, досліджуючи мистецький витвір, зводить весь художній арсенал картини до спрощеної геометричної схеми. Найчастіше художні полотна створюються на основі двох геометричних конструкцій - «золотого перерізу» і спіралі Архімеда. «Золотий переріз» часто пов'язують з ім'ям Піфагора. У його школі, як відомо, вивчали властивості геометричних фігур. На підставі спостережень була виведена математична залежність гармонії АВ:СВ = СВ:АС.

 

Рис.1.1. "Корабельний гай" Шишкін

Вони назвали це «золотим перерізом». Архітектори стародавності знали, що від будівель, споруджених за таким типом, віє теплом і спо­коєм. Навпаки, відчуття динаміки проявляється найсильніше в спіралі. Спіраллю називають плоску лінію, утворену точкою, що рухається, від початку координат за визначеним законом і рівномірно обертається нав­коло свого початку. Перед вами дві картини - «Корабельний гай»  Шишкіна (рис.1.1) і «Побиття малят» Рафаеля Санті (рис.1.2): одна дихає спокоєм і гармонією, друга викликає тривогу, прагнення кудись сховатися.

Рис.1.2. «Побиття малят» Рафаель Санті

Бачите сосну, що стоїть на передньому плані? Вона візуально поділяє картину на два фрагменти - яскраву залиту сонцем галявину і півтінь. Якщо виміряти картину, то виявиться, що довжина картини до сосни так відноситься до довжини всієї картини, як менша відстань до сосни до більшої. Якщо уважно дивитися далі, можна побачити, що кожний із фрагментів картини теж побудований за тим же принципом. Ось відкіля цей урівноважений характер.

Рис.1.3. «Побиття малят» Рафаель Санті

За життя Рафаель не реалізував задум своєї картини до кінця, однак її ескіз був гравірований італійським графіком Маркантоніо Раймонді.

Подивіться на картину і знайдіть її центр, тобто найбільш драматич­ний епізод. Це жінка з лівої сторони, що закриває дитину своїм тілом від удару. Проведіть подумки лінію: руки, голова дитини, голова жінки, голова ката, нога жінки, ще одна жінка, що закриває дитину, і ще одна піднята для удару рука. Ось ця лінія і є «золотою спіраллю» Архімеда (рис.1.3). Ми не знаємо, чи малював її Рафаель, але те, що її побачив Раймонді, - це достеменний факт. Ще одним підтвердженням думки про те, що математика і живопис взаємозалежні, можуть служити роботи голландського художника Ешера.

За минуле XX століття людством накопичений значний досвід наукового прогнозування близьких і віддалених подій. Тому художники все частіше звертають свій погляд у бік зухвалих фантазій. Мистецтвознавці усе впевненіше говорять  про виникнення в наші дні самостійного, двоєдиного жанру наукової фантастики і космічного мистецтва. Зараз у цьому жанрі працюють десятки професіоналів: перші художники-космонавти О. Леонов і

В. Джанібеков, професор математики МДУ А. Фоменко. Він сказав колись: «Живопис прийшов до мене як прекрасний ка­талізатор  наукового  пошуку,   що допомагає  зруйнувати  первинний зв'язок стандартних уявлень і в іншому - асоціативному - світі шукати ключ до розгадування наукових таємниць. У науці лише той, хто здатний фантазувати, хто не відкидає «з порога» парадоксальних ситуацій, може досягти результатів, відкрити несподівані закономірності. Люди, що уміють фантазувати, найчастіше і не підозрюють, яким чудовим дарунком наділила їх природа».

Коли в березні - квітні 1982 року в Москві була відкрита виставка «Учені малюють», преса писала: «За дуже рідкісним винятком художні цінності аматорами не створюються. На виставці «Учені малюють» таким винятком стали роботи А. Фоменка і М. Стерлігової.

Математик Фоменко представив графічні листи, що відрізняються високою оригінальністю і виразністю, фізик Стерлігова - морські пей­зажі і натюрморти. Роботи Фоменка виконані чорною тушшю на папері, Стерліговою - так званою сухою кистю на полотні. І в тому, і в іншому ви­падку техніка дуже складна.

Виставка стала подією тому, що в наш час цікаво і важливо зро­зуміти, як бачать світ і його красу вчені, авіаконструктори, космонав­ти - люди, що беруть активну участь у науково-технічній революції. Навіть на рівні аматорства за наявності відомої художньої культури мож­на написати картини, що виражають це бачення. Але для створення справжніх художніх творів необхідно, як і в науці, набагато більше. Ди­летанти не спроможні нічого.

 

1.2.Математика в архітектурі

До архітектури за всіх часів висувалися три основні вимоги — доцільність, міцність і краса. Ніхто не влаштує собі спальню у високому залі, а для танцювального вечора не вибере кімнатку. Стадіон, театр, бібліотека відрізняються одне від одного і зовнішнім виглядом, і внутрішнім обладнанням. Доціль­ність — обов'язкова відповідність будівлі своєму призначенню.

Про міцність архітектурних споруджень добре сказано в казці про трьох поросят. Краса, гармонія в різні віки була різна. У Єгипті будували колонами. Прикладом цього може служити гіпостильний зал у Карнаку (рис.1.4).  Величезні. Високі колони стоять близько, а стеля ніби тисне згори. У такому «лісі» добре лякати, а людині в ньому моторошно. Так само будували і греки. Балка, балка, а зверху перекриття. Такі будинки могли рости в довжину і ширину. Йшли часи. Цивілізація просувалася на північ. Росли міста, і стала виникати потреба у високих будинках. Цю функцію взяла на себе арка-дуга.

Поставимо руки ліктями на стіл і переплетемо пальці обох рук, — вийде арка. Місце переплетення рук - замок арки. Натисніть підборіддям на нього — і відчуєте легкий біль у ліктях. Тиск по арці розподіляється в усі сторони і дозволяє будувати другий поверх. Крім того, ряди напівкруглих арок дозволяють створити напівкруглий звід. Прикладом такої будівлі може служити Колізей.

З початку свого існування такі споруди не мали даху, оскільки не була розв'язана головна математична задача — як покрити круглий будинок. І от наприкінці 50-х років професор Московського архітектурного інституту М. С. Туполев розробив конструкцію кристалічних куполів, що монтують­ся з рівносторонніх багатокутних пластин. Потім їх розробкою зайнявся доцент Горьківського інженерно-будівельного інституту Г. Н. Павлов. Галузь застосування куполів найрізноманітніша: їх можна використовувати і як виставкові павільйони, і як торго­вельні  зали,   кафе,   ресторани,   складські  приміщення.   А  розміри приміщень є практично необмеженими. Так, у м. Істрі під Москвою по­будований купол із прольотом у 237 метрів. У такий споруді-велетні можна розмістити цілий мікрорайон. Ідея використання кристалічних куполів дозволила архітекторам будувати гігантські 60-метрові круглі будівлі. Таким, наприклад, є виставковий павільйон неподалік від Орландо (Флорида).

Архітектура сьогодні рухається в двох напрямах: 1) конструювання необхідних форм на основі математичних методів; 2) запозичення цих форм у живої природи. Гаслом останнього є такий вислів: «Живі прототипи — ключ до нової архітектури біоніки».

Архітектура другого напрямку втрачає поезію прямого кута, легких округлих обрисів. Але всі ці обриси потрібно обчислити. На допомогу архітекторам приходить геометрія. Вона — посередник між природою й архітектурою. В Україні розробкою геометрії природних форм зай­маються в Київському інженерно-будівельному інституті. У чому ж секрет гармонії природних форм? Ми знаємо, що відрізок — найкоротша відстань між двома точками, а куля — найкомпактніша геометрична фор­ма. Чому ж у живій природі вони не зустрічаються? Проте вони зустріча­ються у своїх похідних. Наповніть кульку водою і покладіть на стіл — вона набуде форми морського їжака. Візьміть кілька однакових кульок, по­кладіть на рівну поверхню так, щоб вони торкалися одна одної, а зверху покладіть на них прозоре скло. Притисніть. Бачите? Кульки перетвори­лися в бджолині стільники.

Архітектурна біоніка розглядає усе: павутину, крило кажа­на - і виникають тенти на гнучкому контурі; симетрію квітів, морських зірок, вітрильників — і виникає, наприклад, будинок оперного театру в Сіднеї (Австралія); розкроюють двостулкові раковини молюсків — одержують купол виставкового залу в Ейндховені (Голландія). Форма крил метелика надихає архітекторів на створення аеропорту в Нью-Йорку.

Архітектурна біоніка має давні корені. Структурними закономірно­стями рослин цікавився ще Леонардо да Вінчі. Рене Декарт на основі ме­тоду координат досліджував криву, що одержала назву «пелюсток жасми­ну», рівняння її х³ +у³ =3аху. У 18 столітті італійський геометр Г. Гранді описав рівняннями сімейство квіток. Німецький математик Б. Хабеніт одержав рівняння листів, плодів, жуків.

Не можна обійтися без геометрії і при перевірці архітектурно-біонічної моделі на міцність. Тут необхідно визначити серединну по­верхню природної оболонки. Неточно побудована серединна поверхня є поганим показником для розрахунку її на міцність. Неабияке значення геометрія має й у художній обробці архітектурних деталей на зразок при­родних форм.

Архітектурна біоніка ще тільки розпочинає свій шлях. Але вже сьо­годні зрозуміло, що це перспективний напрямок в архітектурі.

 

1.3.Математика і музика

Без музики немає фантазії і натхнення. Вона не тільки живе й дихає в серці композитора й артиста, а й рухає поезію та архітектуру, непомітно присутня в усіх глибоких та інтимних почуттях людини.

Просто неможливо уявити собі наше життя без музики. Ми зустрічаємося з нею буквально на кожному кроці.

Послухай: музика навкруг,

Вона невидима в природі

Та для незлічених мелодій

Народжує найкращий звук.

Математика і музика. На перший погляд здається, що нічого спільного в них немає. Але це тільки на перший погляд. Варто лише досконаліше попрацювати над цією темою, і зв'язок відразу відшукається.

Нам, людям XXI століття, життя, що нас оточує, і численні приклади  з історії дають можливість переконатися в тому, яка насправді велика  і різноманітна роль музики. Ми всі добре знаємо, що музика здатна надихати  людей на великі подвиги.

Музика допомагає людям у найважчі хвилини. Як найближчий друг вона втішає в печалі, дає приклад мужнього ставлення до життя.

Німецький математик, фізик і філософ Лейбніц Готфрід Вільгельм (1946-17І6) писав, що «музика є радість душі, яка обчислює, сама того не усвідомлюючи Учення про відношення та пропорції стародавні греки називали му­зикою, яку вважали галуззю математики. Вони знали, що чим слаб­кіше натягнуто струну, тим нижчий («грубіший») звук вона дає, а чим тугіше натягнуто струну, тим звук виший. Але в музичному інстру­менті не одна, а кілька струн. Щоб усі вони під час гри звучали злагод­жено, їх довжини повинні перебувати у певному відношенні. Тому вчення про відношення та пропорції у греків називалось музикою. А музика може справляти на нас незабутнє враження.

Одним із перших, хто спробував дати визначення краси, був Піфагор,той самий Піфагор, теорему якого вивчають у школі. Жив він у VI сто­річчі до н. е., був філософом, астрономом і математиком. Виходячи зі своєї філософії, проблему краси він пов'язував з проблемою гармонії, а гармонія для нього поєднувалася з досконалістю. Він намагався знайти гармонію в числових відношеннях, і звідси пішли музичні гармонії: октава —1:2, кварта — 3: 4, квінта — 2: 3. Відкриття Піфагора поклало початок науці про акустику. Перші звукові прилади було, створено у театрах Стародавньої Греції і Стародавнього Рима: актори вставляли у свої маски маленькі рупори для підвищення звуку.

Евклід (III ст. до н. с.) — видатний старогрецький математик, автор перших теоретичних трактатів, що дійшли до нас. Евклід був невибагливою, навіть скромною людиною, але незалежною. Про останнє свідчить такий факт. Одного разу цар Птолемей запитав Евкліда,чи немає в геометрії коротшого шляху, ніж той, що його пропонує Евклід у своїх книжках. На це Евклід відповів: «Для царів немає окремого шляху в геометрії!» Евклід був різностороннім ученим. До нас дійшли його твори, зокре­ма «Переріз канону», присвячений теорії музики.

   Розмір у музиці — це чергування наголошених і ненаголошених часток, виражених певними тривалостями. Розмір позначається дробом , чисельник якого показує кількість часток у такті, а знаменник – тривалість однієї частки.

Найпростішим розміром, що має найменшу кількість часток, є розмір   , який являє собою чергування однієї наголошеної й однієї ненаголошеної часток.

Дослідженню музики присвячували свої роботи багато відомих математиків: Рене Декарт, Готфрід Лейбніц, Християн Гольдбах, Жан Д'Аламбер, Леонард Ейлер, Данило Бернуллі. Перша праця Рене Декарта - "Compendium Musicae" ("Трактат про музику"), перша велика робота Леонарда Ейлера - "Дисертація про звук». Ця робота 1727 року починалася словами: «Моєю кінцевою метою в цій праці було те, що я прагнув представити музику як частину математики і вивести в належному порядку з правильних підстав все, що може зробити приємним об'єднанням і змішуванням звуків". Лейбніц в листі Гольдбаху пише: «Музика є прихована арифметична вправа душі, що не вміє рахувати". І Гольдбах йому відповідає: "Музика - це прояв прихованої математики»  

Чому ж прихованої? Адже в Стародавній Греції музика прямо вважалася частиною математики, а ще точніше, розділом теорії чисел. Першим, хто спробував висловити красу музики за допомогою чисел, був Піфагор - той самий, чиїм ім'ям названа знаменита теорема. І в XVII столітті французький філософ, фізик, математик Марен Мерсен в трактаті «Істина наук проти скептиків або піроніків" також розглядав музику як галузь математики.

Піфагор був не лише математиком і філософом, а й теоретиком музики. Він займався пошуками музичної гармонії, оскільки вірив у те, що така музика необхідна для очищення душі і лікування тіла і здатна допомогти розгадати будь-яку таємницю. Одного разу, проходячи повз кузню, Піфагор випадково почув, як удари молотів створюють цілком певне співзвуччя, і після цього зайнявся експериментами, намагаючись знайти співвідношення між висотою тону і числами. За допомогою чаші з водою і однострунної арфи він вивчив взаємозв'язок між рівнем води і довжиною струни і виявив, що половина довжини струни піднімає ноту на одну октаву вгору.

Піфагорова теорія музики досягла навіть небес. Піфагор поділяв уявлення про сферичності світобудови і при цьому першим назвав Всесвіт «космосом». У ті часи крім Землі, Місяця і Сонця були відомі тільки Меркурій, Венера, Марс, Юпітер і Сатурн. Але ще Піфагор припустив існування «анти-Землі» і при цьому виділяв 10 небесних тіл. Зрозуміло, це твердження було тоді чисто теоретичним: число «10» для нього символізувало гармонію Всесвіту. Пізніше він захопився ідеєю «музики сфер», прагнучи пов'язати консонантні (гармонійні) звуки з планетарними сферами. Він виходив з того, що інтервал в просторі між планетами - той же, що і шкала висоти музичного звуку. Кожна планета, рухаючись з постійною швидкістю, проходить певну відстань, створюючи звук. У міру того як відстань планет від центру збільшується, а обертання планет прискорюється, звук стає вище. Саме так Піфагор уявляв собі музику, яка звучить по всьому Всесвіті.

Співучі зорі? Дивовижно! Йдеться про звуки, які могли б видавати планети Сонячної системи під час ідеального руху по своїх орбітах, звуки, які нині вченим вдалося записати на платівку за допомогою синтезатора. Можна сказати, що народженню такої музики сприяли багаторічні пошуки музикантів, мистецтвознавців, математиків, ас­трономів, кібернетиків. Вони синтезували музику зоряного неба за допомогою обчислень, які провів у XVII столітті один з найвидатніших астрономів і математиків — Йоганн Кеплер.             

Коли Кеплер відкрив закони руху світил, він висунув гіпотезу про існування пов'язаної з ними... музики! Вчений обчислив швидкості планет і переклав їх на тони. Кеплер намагався переконати сучас­ників, що музика зірок є «безперервною піснею для кількох голосів, і які вловлюються розумом, а не вухом». За допомогою електрон­но-обчислювальної техніки вчені дали можливість нам цю музику почути.

«Пісня» кожної планети — це результат її розмірів, форми і зміни швидкості руху. Меркурій, наприклад, тихо посвистує. Венера звучить у діапазоні четверті тону, а Земля «співає» трохи сумну полутонову ме лодію. У той же час Марс видає звуки зі швидкими переходами, що охоплюють широкий діапазон тонів. Треба зазначити, що не лише Кеплер цікавився музикою зоряного неба. Схожі передбачення робилися ще за часів Піфагора. Проте деякі  математики, які брали участь в «озвученні» математичних величин;, стверджують, що ніякої гармонії тут немає, а є тільки точне об'єднання формул Кеплера, перетворених на абстрактні звуки музики .

 Про вплив музики на людину з давніх давен було добре відомо багатьом     Піфагор стверджував, що «музика дуже благотворно діє на здоров'я, якщо займатися нею належним чином». Тому піфагорійці, «відходячи до сну, ... очищали розум від денного сум'яття і шуму певними піснями й особливого роду мелодіями і цим забезпечували собі спокійний сон з небагатьма і приємними сновидіннями ». Одного разу Піфагору вдалося вгамувати гнів п'яного дебошира юнака просто тим, що він звелів флейтисту зіграти урочисту мелодію. Тим самим філософ не тільки відкрив цілий ряд музичних ефектів, але і знайшов їм практичне застосування в навчанні та медицині.

З давніх пір до нас дійшов афоризм, що математика і музика - сестри. А здавалося б, що спільного між наукою, що користується суворої логікою доказів при вивченні природи і музикою - одним з прекрасних видів мистецтва, твори яких створюються в пориві натхнення?

Давньогрецький філософ Піфагор, один з найперших встановив зв'язок між музикою і математикою. Він створив вчення про звук, вивчав філософський і математичний аспекти звуку, навіть намагався пов'язати музику з астрономією. Використовуючи особливий інструмент - монохорд, Піфагор вивчав інтервали, відкривав математичні співвідношення між окремими звуками. Піфагор розвинув вчення про лікуванні хвороб за допомогою музики. Він вважав, що певні мелодії можуть позбавити людину від заздрості, ревнощів, гордині та інших вад.

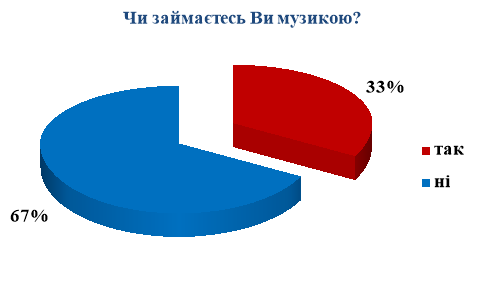
Отже, музика математична, а математика музична. І там, і тут панує ідея числа і відношення. В грандіозному обстеженні 25000 американських школярів, що займаються за арт-програмами, було особливо відмічено, що діти, які навчаються музиці, показали в математичних тестах бали вищі, ніж діти, що музиці не навчались.

Ми теж вирішили перевірити як музика впливає на успішність учнів нашого закладу з математики і отримали такі результати.

Діаграма 1.1

 

Діаграма 1.2

 

 

 

 

Діаграма 1.3

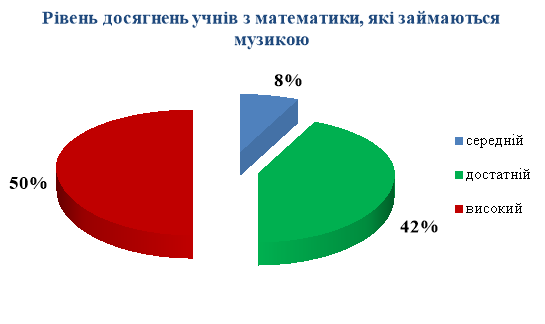
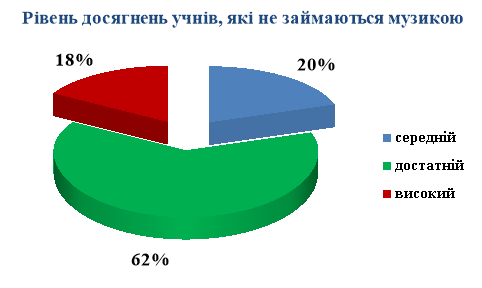
З діаграм 1.2 та 1.3 бачимо, що кращий рівень досягнень мають ті учні, які займаються музикою. Що і потрібно було довести.

1.4. Фрактал – математика мистецтва

У  другій  половині  минулого століття  Бенуа Мандельброт  виявив,  що  в  природі практично всюди присутня одна загальна властивість її компонентів, на яку до нього майже не звертали уваги, –  самоподібність.  Вона  полягає  в  тому,  що ціле  складається з  частин,  які  є  його  власними точними або приблизними зменшеними копіями.

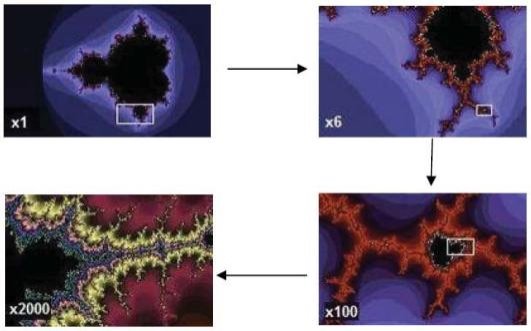
Рис.1.7. Генерування фракталів – множина Мандельброта

Самоподібність характерна як для природних об'єктів, так і для більшості процесів, що відбуваються в природі (розмноження сарани з вибухами і провалами в їх чисельності, потоком рідини разом з виникаючими при  цьому  завихреннями), включаючи навіть ті процеси, які пов'язані з діяльністю людини, або нею викликані(як, наприклад, коливання ринкової вартості цінних паперів). Ця  властивість  і  стала  основною, характерною  ознакою  фракталів (рис.1.8).  Нова властивість  виявляє  своєрідну  симетрію  фракталів.

Звичні види симетрії дозволяють відображати частини відносно прямої або точки. Майкл Барнслі, що розробив метод фрактального стиснення зображення, почав свою книгу ״Фрактали всюди״  так: ״Фрактальна  геометрія  змусить  Вас  на все дивитись іншими очами. Далі читати небезпечно, Ви  ризикуєте  втратити  все  дитяче  уявлення  хмар, лісів, галактик, листя, квітів, скель, гір та багато чого іншого. Ваше сприйняття цих речей ніколи більше не буде як колись. Дійсно, різновиди живої природи,  множина рослин та ландшафтів, простір та космос,  середовище людського існування– усе це складене з  малих  елементів,  частинок,  що  повторюючись,  утворюють сукупність, систему.

 

                                  Рис.1.8. Фрактальні структури

Фрактал (лат. Fractus – подрібнений, дробовий) сама по собі нерегулярна, самоподібна структура. В широкому розумінні він означає фігуру, малі частини якої  в  довільному  збільшенні  є  подібними  до  неї самої. Термін фрактал було введено у1975 р. Бенуа Мандельбротом. Фрактали по своїй суті відображають усі  органічні  структури  живої природи,  показують,  як із дуже малих структур утворюються рослини і тварини. Приблизні фрактали можна легко знайти в природі. Ці об'єкти мають самоподібну структуру при великих, але обмежених діапазонах збільшень.

На  сьогоднішній  день  фрактали  широко використовуються у комп’ютерній графіці для побудови зображень природних об’єктів, таких як дерева, кущі,  гірські ландшафти,  поверхні  морів  і  т.  д.  Подібну до  фрактальної  має система  кровоносних  судин.  Геометричні фрактали застосовуються для отримання зображень  дерев,  кущів,  берегових  ліній  тощо. Алгебричні та стохастичні – для побудови ландшафтів,  поверхні морів, моделей біологічних та інших об'єктів.

 Дослідження  і  глибоке  вивчення  геометрії фракталів та можливостей їх художнього використання почалося вже в ХХ ст. з появою достатньо потужних обчислювальних  машин.  Виникли  напрямки  в сучасному мистецтві, які, базуючись на математичних формулах, створюють емоційно и кольорово насичені фрактальні картини.

Фрактальна  графіка  є  досить  багатогранною.  Фрактали (фрактальні  структури,  множини)  використовуються у мистецтві для створення художніх творів  у  стилі  імпресіонізму (зокрема  Джексон Поллок, митець 50-х  років,  малював  об’єкти,  дуже схожі на фрактали), графічному дизайні, індіанському та  африканському  мистецтві. Принцип  фрактальної самоподібності був також використаний при створенні Ейфелевої вежі.

Водночас  слід  зазначити,  що  перші  згадки про фрактал з’явилися ще в Середні віки. В 1525 р.  німецький митець Альбрехт Дюрер опублікував свою працю ״Керівництво Художника״, один із розділів якої має назву ״Черепичні шаблони, утворені пентагонами״.  Пентагон Дюрера багато в чому є схожим на один з фракталів,  але  замість  квадратів  використовуються п’ятикутники. В роботах Рона Еглаша ״Африканські фрактали״ задокументовано  поширені  фрактальні геометричні структури мистецтва тубільців.

Найглибші  дослідження  фрактальних  множин на  той  час  провів Удо  Аахен,  відомий  в  історії  як поет, літописець та теоретик-іезуїт. Дата народження та  смерті  цього  бенедегтинського  монаха  були невідомі. Вірогідно, він жив приблизно у1200-1270 рр. н.е. Нове вивчення його праць представило Удо, як  високоосвідченого  та нестандартно  мислячого  і талановитого математика і митця.

На сьогоднішній день Удо не є таким відомим як одна з його робіт. Цей монах ХІІІ ст. – автор поеми ״Fortuna ״Imperatrix Mundi״ (״Вдача ״Імператриця світу״), що відома сьогодні як mina Burana. Вперше не вивченні можливості Удо були відкриті математиком Бобом  Шипку, професором  комбінаторики.  Під  час відвідання  Аахенського собору,  вчений  побачив те,  що  його  вразило.  На  одному  з манускриптів ХІІІ  ст.  він  помітив  Зірку  Віфлеєму,  що  виглядала дивно. Придивившись до деталей, побачив Фрактал (мандельборську функцію) – одну  з  ікон  нашого комп’ютерного часу (рис. 1.9.а,б).

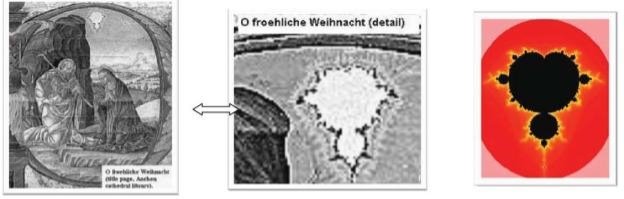
Рис. 1.9. а – ікона «Imperatrix Mundi», б –Imperatrix Mundi, наближений фрагмент,в – Множина Мандельброта –фрактал

Відкритий  у 1976  р.  науковцем  компанії ІВМ  Бенойтом Мандельбортом,  цей  фрактал –  математичний об’єкт з властивостями геометричної прогресії. Тільки з появою швидкісних комп’ютерів його визначення стало можливим (рис.1.9. в)

Монах  Удо  займався  вивченням  математики, простих  і  складних чисел,  дослідженням  теорії вірогідності,  правилами  їх  множення  та  поділу  за кількома категоріями. Спочатку мета Удо була в тому, щоб  розробити  метод  для  визначення  можливості досягти небес. Він припускав: душа кожної людини складається  з  двох  незалежних частин, «profanus» (мірське)  і«Animi» (духовне),  які  представляв  за допомогою  пари  чисел.  Згодом  монах  розробив правила для складання та маніпулювання цими парами чисел,  що,  по  суті, являли собою  складні  правила арифметики, духовна і мирська частини, відповідали дійсним і уявним числам сучасної математики. 

Таким чином,  шляхом  безкінечної  кількості розрахунків, складання та множення, крапка за крапкою була  створена  множина Мандельброда. Удо  вдалося визначити цю множину за сім віків до, власне, її відкриття в сучасній науці. Монах тлумачив її як щось Божественне, Вищу Сутність, наукове вираження духовного початку.

Він  не  зміг завершити  працю,  довести  свої пошуки  до  логічного кінця, працюючи  один.  Та  й суспільство було не готове сприйняти ці дослідження.  І все ж таки ця знахідка є унікальною. Будучи водночас і науковцем, і художником, Удо Аахен поєднав свої знання і відобразив їх у такий специфічний спосіб, як у нікому незрозумілий і невідомий фрактал, як зірка Віфлієму, символ божественного початку.

На  рисунках 1.10-1.13  наведені  фотографічні зображення  елементів природи  та  поряд  з  ними –  утворенні автором за допомогою комп‘ютерної графіки через  программу Tierazon – малюнки самоподібних фракталів (вони вже містять в собі художній задум та творчі елементи).

        Порівняймо їх. Так, наприклад, морські мушлі є одним з найяскравіших прикладів фракталу в природі. Вони закручені, елементи повторюють один одного,  збільшуються або зменшуються в геометричній  прогресії (рис.1.10).

Космос, незвідані галактики, їх системна структура, шароподібність, планети, що рухаються  по колу – все це є фрактальною самоподібністю у вселенському масштабі  (рис.1.11).

Найменші клітині живого організму – хромосоми та атоми – є прикладами

фракталів. Будова людського тіла заснована на повторенні атомів та молекул, що складаються в органи, тканини та кістки. ДНК – має спіральну самоподібну будову, в якій кожен елемент є важливим. Зміщення навіть одного елементу призводить до втрати всієї структури (рис.1.12, а-б).

Рис. 1.10. Спіраль

                       Рис.1.11. Космос, а – метеорит, б – всесвіт

Наша планета придатна до життя завдяки зеленим лісам та рослинам. Подивимось на внутрішню структуру листка, в ньому все узгоджено та побудовано, елементи повторюються и складають єдине ціле (рис.1.13). Кожне дерево має стовбур та відгалуження – гілля та листя, без цього його існування  не можливе. За таким принципом повторюваності побудована флора нашої планети.

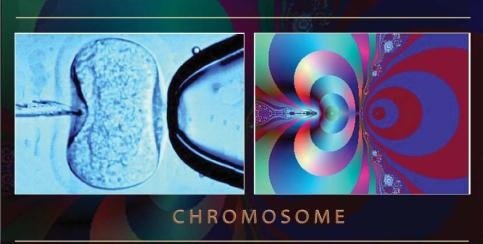
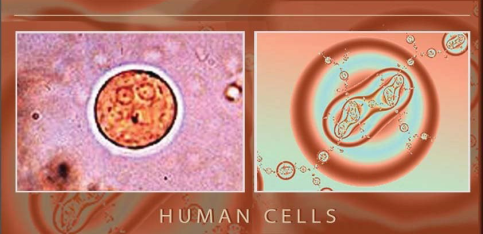
Рис.1.12. а – людська клітина, б – хромосома

     

Рис.1.13. Листя

Звернемося до фауни. Вчений-біолог та дослідник Геккель на своїх малюнках зобразив найпростіші мікроорганізми (радіолярії, губки та медузи), що є  частиною планктону (рис.1.14), порівнявши їх структурну організацію з типологіями відомих фракталів. Вони дійсно схожі. Так, можна зробити однозначні висновки стосовно самоподібності їх побудови та інваріантності. Прикладів самоподібності в живій природі існує багато: гордовий павич, завмерлі мінерали, гірські масиви та кришталі, льодові нарости та річкові басейни. Їх структура побудована в жорсткій послідовності елементів, молекул та атомів.

Рис.1.14. Зображення радіолярій, губок та медуз Геккеля

На основі проаналізованого матеріалу виявлено існування геометричних, алгебраїчних, стохастичних  фракталів, які широко використовуються у комп’ютерній графіці для побудови зображень як природних об’єктів, так і систем неприродного  походження.

Показано, що фрактальна сфера дії охоплює і процес художньої творчості, перехід від почуттів і уявлень – з внутрішнього світу митця – до кінцевої  картини – графічного твору.

РОЗДІЛ ІІ

Математика і мистецтво – фундаменти освіти

 

2.1.Математика та кіно

Математика завжди була однією з основ розвитку дитини. У сучасному світі уже неможливо уявити, щоб діти не знали що таке математика. А любов до такого логічного, розумного і трохи нудного, на перший погляд, предмету прививають дітям з самого малечку. Найкраще це роблять - мультфільми, адже діти обожнюють їх і залюбки дивляться.

Мультфільм у легкій і грайливій формі подає матеріал складних математичних задач. Таких прикладів мистецтва є безліч, деякі з них:  «Лунтик», «Даша-дослідниця», «Маша і ведмідь». Це мультики для малят, які навчають арифметики. Також дуже часто арифметика зустрічалася в радянських мультиках, наприклад: «Вовочка в тридев'ятому королівстві», «Дюймовочка»,  «Трям! Здравствуйте!» та інші. Ці мультики показують дітям, що математика є всюди, що без неї і будинок не побудуєш, і гроші не порахуєш і загалом це веселе заняття рахувати.

Математика - це спосіб вираження душі деяких людей, як малюнок для художника, як вірш для поета. Ось таку математичну душу показують глядачам фільми, які привертають вже доросле покоління: «Гра в імітацію»,  «Ігри розуму» та інші. Дорослі дивлячись таку пригодницьку математику, люблять її ще більше і коли в реальному житті вивчення її набридає, такі шедеври кіно знову по-новому демонструють дивовижний світ чисел і логіки, який допоможе їм у реальному житті.

Математика з таким частим використанням стала важливою частиною кіномистецтва. І перетворилася на мистецький шедевр, який створюють математики, використовуючи безліч чисел у своїй голові.  Математика в кіномистецтві стає сама мистецтвом, навчаючи, надихаючи і розвиваючи людей, а отже і цілий світ.

В ході пошукової роботи ми знайшля ряд художніх фільмів, в яких є персонажі - математики, або згадки про них:

-21 Grams (2003) - Випадок змінив багато життів, включаючи життя критично хворого профессора математики (Шон Пенн);

-Агора (2009) - Фільм про життя Гіпатії;

-Antonia (фільм) (1995) - Генеалогічна "лінія" п'яти поколінь жінок, включно з вундеркіндом, Терезою, яка виростає щоб стати математиком;

-Ігри розуму (2001) - Вигадана історія, яка базується на житті математика Джона Неша (Рассел Кроу), яки зробив прорив в теорії ігор що забезпечило йому Нобелівську премію з економіки;

-Банк (2001) - Математик відкриває формулу що передбачає флуктуації на біржевому ринку;

-Енігма (2001) - Історія романтичної та психологічної інтриги протягом другої світової війни, при спробах зламати німецький шифр Енігма;

-Кімната Ферма (2007) - Три математики та один винахідник запрошені в будинок під приводом розгадування великої загадки. Їх попросили використовувати псевдоніми які є іменами історично відомих математиків. В будинку вони попадають в пастку. Вони мають розв'язувати загадки господаря, який називає себе "Ферма", щоб втекти з будинку;

-Розумник Вілл Хантінг (1997) – Прибиральний Вілл Хантінг (Метт Деймон) починає змінювати своє життя з допомогою психолога (Робін Вільямс) та професора що отримав Медаль Філдса;

- I.Q. (1994) - Альберт Ейнштейн (Волтер Меттау) допомагає хлопцю (Тім Роббінс) притворятись фізиком щоб привернути увагу племінниці Ейнштейна (Мег Райан);

-Зараз мій хід (1980) - професорка математики (Джил Клейбург) закохується в сина нареченої свого батька (Майкл Дуглас);

-Парк Юрського періоду (1993) – математик (Джеф Голдблум) серед тих хто запрошені в тематичний парк з клонованими динозаврами, щоб оцінити його безпеку;

-Дзеркало має два обличчя (1996) - професор математики (Джефф Бріджес) одружується на професорі літератури (Барбра Стрейзанд), але вони хочуть від стосунків різного;

-N це число: Портрет Пола Ердеша (1993) документальний фільм про життя угорського математика Пола Ердеша;

-Вбивства в Оксфорді (2008) - студент (Елайджа Вуд) розгадує таємниці вбивства зі своїм профессором;

-Пі (1998) - Математик шукає число що відкриває все, від коливань фінансових ринків, до імені Бога в Каббалі;

- Доведення (2005) - Колишній студент (Джейк Гулленхал) математика що недавно захворів (Ентоні Гопкінс) знаходить записник в офісі, що містить доведення важливої теореми, проте донька математика (Гвінет Пелтроу) стверджує що він;

-Зростаючий геній (2004) - Фільм про хлопця (Джастін Лонг) який закрив себе в ванній щоб спокійно опрацювати рівняння;

-Кеди (1992) - збирається команда яка має вкрасти криптоаналітичний пристрій розроблений лихим математиком.

2.2.Математичні вірші

Ми відкрили для себе дивовижну новину. Виявляється, математика не лише цікава та захоплююча наука, а ще й поетична. Неймовірно, та вірші можна писати не тільки українською, російською чи англійською, але й мовою цифр.

На жаль, невідоме ім’я того умільця, котрий вперше вигадав творити поезію за допомогою цифр. Та від того вірші математичного генія не менш популярні.

Прочитай наступний цифровий шедевр та спробуй відгадати, вірші якого поета в ньому зашифровані.

17 20 48

140 10 01

126 138

140 3 501

Це знамениті рядки Олександра Пушкіна з листа Тетяни Євгенію Онєгіну:

 «Я к вам пишу — чего же боле?

Что я могу еще сказать?

Теперь, я знаю, в вашей воле

Меня презреньем наказать…»

А в цьому математичному вірші зашифрована пісенька.

2 15 42

42 15

37 08 5

20 20 20!

7 14 100 0

2 00 13

37 08 5

20 20 20!

Все просто! Це пісня «Кабы не было зимы» з нашого улюбленого мультфільму «Зима в Простоквашино».

 «Кабы не было зимы

В городах и сёлах,

Никогда б не знали мы,

Этих дней весёлых.

Не кружила б малышня

Возле снежной бабы

Не петляла бы лыжня,

Кабы, кабы, кабы...»

Наступний вірш відгадати не складно. Неймовірно, наскільки точно автор вирахував рими!

511 16

5 20 337

712 19

2000047

3 1512

16025

11 0 3 15

100006 0 2 3

Це вірш «Я помню чудное мгновенье» Олександра Пушкіна.

 «Я помню чудное мгновенье:

Передо мной явилась ты,

Как мимолетное виденье,

Как гений чистой красоты.

В томленьях грусти безнадежной

В тревогах шумной суеты,

Звучал мне долго голос нежный

И снились милые черты.»

2.3.Математика в художніх творах

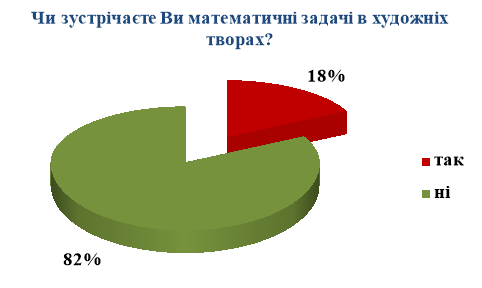
Ми провели цікаве дослідження в цьому напрямі серед учнів нашого закладу. Результати анкетування показали, що 82% опитаних респондентів не звертають увагу на задачі в літературі, а ті що їх зустрічають (18%) – не намагаються їх розв’язувати.

Діаграма 2.1

Діаграма 2.2

 

      

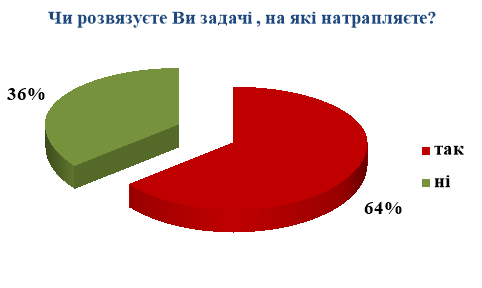
З метою підвищення інтересу до математики, ми вирішили провести позакласний захід на тему «Математика в художніх творах» для учнів 6-х класів. Наведемо деякі фрагменти даного заходу.

Рис.2.4.Уривок з твору про Гаррі Поттера

Рис.2.5. Жюлб Верн «Таємничий острів»

Рис.2.6. Мультфільм «Зарядка для хвоста»

Фото 2.1. Учениці 11ЕК класу проводять захід для учнів 6Б класу

Фото 2.2. Учні 6Б класу під час проведення заходу

Слід сказати, що ми зацікавили шестикласників. Деякі учні одразу захотіли прочитати твір «Таємничий острів». Багатьом було цікаво вимірювати зріст папугами та мавпами. Маємо надію, що в майбутньому ці діти будуть багато читати літератури та шукати математичні задачі в літературі, а в найкращому випадку – розв’язувати знайдені задачі.

Фото 2.3. Учні 6А  класу під час проведення заходу

2.4. Нумеризм Сієни Моріс

  Наскільки правий був Андре Моруа, який написав в 1919 році новелу «Народження знаменитості». Однією працею і талантом не досягнеш успіху.

«Щоб стати відомим, потрібно зважитися на якусь витівку або створити нову школу. Змішати в одну купу всілякі розумні слова, ну скажімо екстеріорізація, динамізм, підсвідомість, безпредметність - і скласти маніфест! Заперечувати рух або, навпаки, спокій, біле або чорне, коло або квадрат - це байдуже! Вигадати якийсь неогомеричний живопис», що визнає тільки червоні та жовті тони, «циліндричну» або «октаедричні», «чотиривимірну» яку завгодно! »...

Рис.2.7. Нумеризм Сієни Моріс

 Не знаємо, чи читала Сієнна Морріс (Sienna Morris) цю новелу, але пішла вона цим шляхом, придумавши техніку написання картин з використанням цифр і математичних рівнянь і назвала її нумеризм (numberism).

 У своїх роботах художниця прагне відобразити яскраві моменти життя і показати їх швидкоплинність. Одна з її картин, на якій зображений равлик, намальована числовою послідовністю Фібоначчі, де кожне наступне число дорівнює сумі двох попередніх чисел (рис.2.7).

 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 ....

 На думку художниці, це ідеальна спіраль, яка в природі зустрічається у равликів.

Інший приклад наукового підходу до мистецтва - зображення «Schröedinger s Cat» (рис.2.8), намальоване за принципом невизначеності Гейзенберга.

Рис.2.8 . Нумеризм Сієни Моріс

Ідея створення текстури за допомогою точки або символів не є новою , але це не було зроблено за допомогою цифр і символів, які мають значення для суб'єкта, каже професор художньої практики Пет Боаш

Сієна Морріс , яка завжди захоплювалася математикою і природничими науками, часто проводить час, досліджуючи числа і формули для майбутніх робіт

Рис.2.9. Нумеризм Сієни Моріс

«Вона не просто малює числа і формує з них зображення, вона дійсно відчуває їх , і цифри не просто цифри, це спектр шляху процесу людини».

Ця техніка роботи надихнула і ученицю нашого класу Самійленко Олену (фото 2.4) на творчість. Олена – наша Сієна Моріс, переможниця багатьох конкурсів, організаторка власної художньої виставки, за допомогою комп’ютерної графіки створила власні картини із цифр.

Рис.2.10. «Місяць» Самійленко Олена , учениця 11ЕК класу

Фото 2.4.Самійленко Олена, учениця 11ЕК класу

 

Рис.2.11. «Тигр» Самійленко Олена , учениця 11ЕК класу

2.5. Математика і спеціальність «комп’ютерний дизайн»

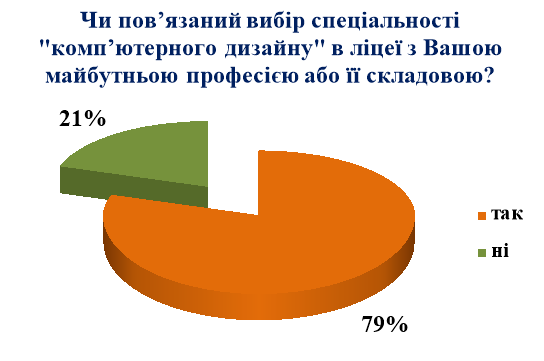
Ми провели анкетування серед дизайнерів закладу. Опитано було 29 учнів. Результати анкетування виявились такими:

Діаграма 2.3

Діаграма 2.4

Діаграма 2.5

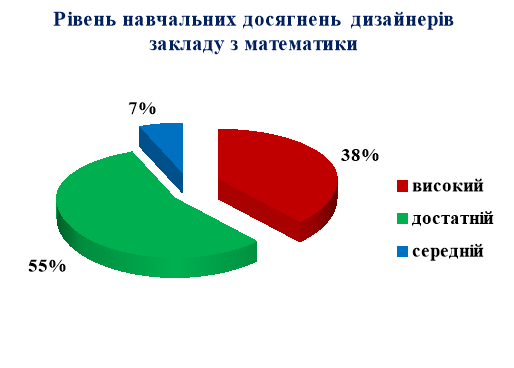
Діаграма 2.6

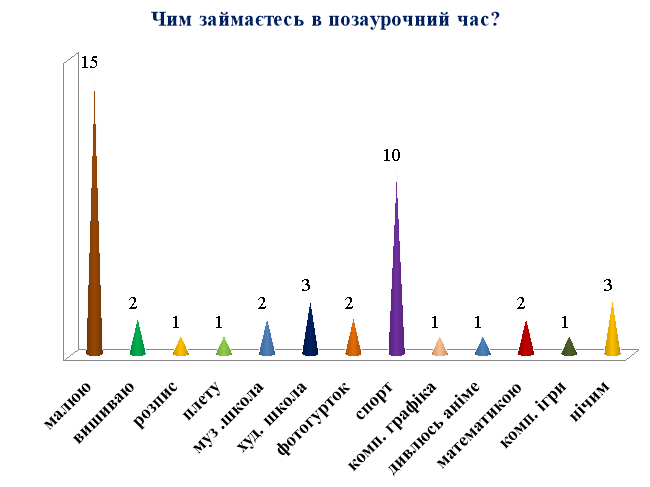
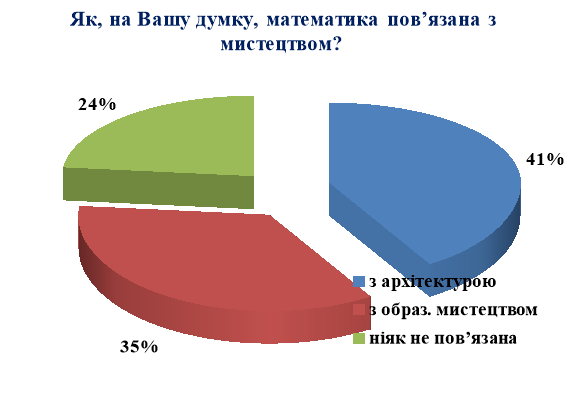
З діаграми 2.4 бачимо, що все ж таки більша частина учнів 79% свідомо обрали дану спеціальність, але 21 % учнів ще не визначились у виборі професії. Діаграма 2.5 показує, що ліцеїсти мало знайомі з різними видами мистецтва тому, що назвали лише архітектуру та образотворче мистецтво. Один учень вважає, що математика потрібна лише для того, щоб рахувати гроші зароблені за допомогою мистецтва. Оцінюючи рівень навчальних досягнень дизайнерів закладу, слід сказати, що високий рівень мають учні, які відвідують художню та музичну школи, займаються у фотогуртку, малюють, вишивають та плетуть.

Відповідаючи на питання про майбутній ВУЗ, дизайнери обирали КНУБА (Київський національний університет будівництва і архітектури), ДНУ(Дніпропетровський національний університет), ЛНАМ(Львівська національна академія мистецтв), ІДПМ ім.Бойчука (Київський державний інститут декоративно-прикладного мистецтва і дизайну імені Михайла Бойчука) та інші. Ми також поцікавились спеціальностями пов’язаними з архітектурою. Підібрали декілька вузів України і побачили, що на таку спеціальність для вступу потрібно у сертифікаті ЗНО мати  результати тестування з математики та при вузі абітурієнти беруть участь у творчому конкурсі (малюнок – комбінація геометричних тіл). Назвемо деякі зних:

• Київський національний університет будівництва та архітектури;
• Національний авіаційний університет;
• Одеська державна академія будівництва та архітектури;
• Львівський національний аграрний університет;
• Національний університет Львівська політехніка;
• Донбаська національна академія будівництва і архітектури;
• Національна академія образотворчого мистецтва і архітектури;
• Чернівецикий національний університет ім.Федьковича;
• Харківський національний університет будівництва і архітектури;
• Полтавський національний технічний університет;
• Придніпровська державна академія будівництва і архітектури м.Дніпропетровськ та інші.

Тому хочемо порадити майбутнім дизайнерам-архітекторам більше часу присвятити вивченню саме математики.
           Висновок

Для багатьох світ математики – це тільки задачі, формули, перпендикуляри, трикутники… (як говорять: сіра та суха наука). Але для декого цей світ здається різнокольоровим, яскравим, цікавим та загадковим. Тому їм вдається самим бачити світ людей у всіх кольорах веселки!!!! Хоча не всі їх  розуміють (можливо  через свою  «близорукість»).

З   докором в адресу математиків звучать слова Ешера - людини, яка він рахував, далека  від  математики: «Математики відкрили двері ,що ведуть в інший світ, але самі ввійти в цей  світ не наважились. Їх більше цікавить шлях , на якому стоять двері, ніж сад, що лежить  за нею...».

Можливо потрібно  приивідкрити  ці двері  та переконатись ,що  світ,що знаходиться за дверима зможе здивувати, вразити своєю красотою та незвичайністю, пробудить інтерес до нескінченно невідомого в математиці, чарівні таємниці якої   не видно за вереницею формул…

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Гринченко В. Т., Мацыпура В. Т., Снарский А. А. Фракталы : от удивления к рабочему инструменту. К.: Наукова думка, 2013. 270 с.
2. Михайленко В. Е. Природа. Геометрия. Архитектура.- К.: Будівельник, 1981.
3. Гозарян С. В мире музыкальных инструментов.— М.: Освіта, 1989.
4. Техника молодежи.- 1983.- № 1.- С. 3; № 7.- С. 23.
5. Квант.- 1988.- № 6.- С.11.
6. Квант.- 1984.-№9.
7. Квант.-1990.-№12.
8. Наука и жизнь.- 1986.-№ 5.-С 86.
9. http://matematichka.at.ua/publ/cikava_matematika/matematika_v_mistectvi
10. http://livescience.ru/Статьи:Музыка-математика-в-цифрах
11. http://alexfrost.ucoz.ru/index/music
12. http://kuncevo.ucoz.ru/load/uroki/matematika/matematika_i_muzika_vechir
13. http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
14. http://worldhobbies.ru/kreativnue-hobby/numerizm-siennyi-morris