Науково дослідницька робота

ДЕПАРТАМЕНТ ОСВІТИ І НАУКИ ЛЬВІВСЬКОЇ ОБЛДЕРЖАДМІНІСТРАЦІЇ

СОКАЛЬСЬКИЙ РАЙОННИЙ ВІДДІЛ ОСВІТИ

СОКАЛЬСЬКА МАЛА АКАДЕМІЯ НАУК УЧНІВСЬКОЇ МОЛОДІ

 

 

 

 

 

 

 

 

Науковий керівник: Кровіцька Лариса Ярославівна, вчитель математики Сокальської Малої академії наук учнівської молоді

ВИПАДКОВА ВЕЛИЧИНА ТА ГРА ЯК МОДЕЛЬ ПРОЦЕСУ ПРИЙНЯТТЯ РІШЕННЯ В УМОВАХ РИЗИКУ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

Вступ…………………………………………………………………………....3

Розділ 1.

Ймовірний простір як модель випадкового випробування………………………...………..………………………….....5

1.     Ймовірнісна модель випадкового випробування………………………….5
2.     Класичний імовірнісний простір…………………………………………...5

Розділ 2

Випадкова величина та ймовірнісний простір,який вона утворює на числовій осі………………………………………………..7

1. . Результат випадкових випробувань.……………………………………......7

2.     Функція X – випадкова величина ……………....……………..…………...8

Розділ 3.

Процес прийняття рішення в умовах ризику і в Ситуації невизначеності…………………………………………………..................10

3.1. Людська діяльність – процес з математичної точки зору………………....10

3.2. Випадкова гра як модель процесу прийняття рішення в умовах ризику...13

3.3. Математичне сподівання – прибуток салону азартних ігор………………16

3.4. Випадкова гра як модель деяких життєвих процедур……………………..18

Висновки……………………………………………………………………….21

Список використаних джерел…………………………………….......22

 

 

 

 

 

 

 

 

 

Вступ

«Розв’язування задач є найхарактернішим і

специфічним різновидом вільного мислення.»

В.Джеймс

Захоплення математикою здебільшого починається з роздумуванні над якоюсь цікавою задачею, над ідеєю її розв’язку. Вона може зустрітися на уроці або на занятті математичного гуртка, або у книжці. Завдання сучасної школи – виховати особистість, яка думає самостійно. Знання, навички й уміння – не реальні предмети, які можна передавати. Їх здобувають у результаті власної активної діяльності. Чимало своїх зусиль людина витрачає на пошук ідеї розв’язування поставленої задачі.

Мета: дослідити розв’язування життєвих проблемних ситуацій за допомогою комбінованих формул в класичних імовірнісних просторах, навчитися приймати рішення в умовах ризику і в ситуації невизначеності за допомогою математики.

Ідея: розв’язування нематематичних задач з теорії ймовірностей, що стосується навколишнього світу є ілюстрацією справжнього процесу застосування математики. Стратегічно випадкова гра моделює реальні ситуації, з якими має справу учень у своєму повсякденному житті.

Ідея роботи має практичне застосування, адже задачі, які досліджувалися, використовуються на факультативних заняттях, між предметних факультативах, на олімпіадах з математики.

Дидактика математики шукає джерела цікавих для школярів проблемних ситуацій, на фоні яких виникають справжні задачі з теорії ймовірностей. Йдеться про задачі, які дають учню відповідь на запитання: кому, в яких обставинах і навіщо можуть знадобитися стохастичні поняття й методи, в тому числі й висновки, специфічні для цього розділу математики?

Основними поняттями теорії ймовірностей є поняття ймовірнісного простору, поняття події та її ймовірності, випадкової величини, її розподілу та її математичного сподівання. Розглянемо декілька життєвих прикладів, а отже, нематематичних проблемних ситуацій, на фоні яких з’являються запитання, які можна перекласти на мову математики, а потім відповісти на них за допомогою математики.

Це, наприклад, такі запитання:

Яке прийняти рішення?

Яку встановити платню за участь у грі в салоні азартних ігор, щоб цей салон процвітав?

Тим самим згадані ситуації ілюструють, що яким чином і якими засобами, а передусім навіщо математизується в теорії ймовірностей.

Зміст шкільних задач з теорії ймовірностей можна знайти в навколишньому світі.

Усі проблеми розв’язуються в класичних ймовірнісних просторах. Ймовірність події обчислюється в такій ситуації за допомогою комбінаторних формул.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 1 Ймовірний простір як модель випадкового випробування

1.1. Ймовірнісна модель випадкового випробування

Ймовірнісним простором будемо називати пару, де - це довільна непорожня та скінченна множина, а р – функція, яка відображає множину в множину R дійсних чисел ( р :  R) і задовольняє систему умов:

для кожного і

Функція р називається розподілом ймовірності на множині . Ймовірнісні простори є моделями випадкових випробувань, тобто явищ, дослідів, результати яких випадкові.

Якщо множина ідентифікує всі можливі наслідки випадкового випробування і для кожного число є ймовірністю того, що випадкове випробування закінчиться результатом (наслідком) , то пара (, р) – це ймовірнісна модель випадкового випробування.

 

1.2. Класичний імовірнісний простір.

 Якщо - s-елементна множина і для кожного , то функцію р називають класичним розподілом ймовірності на множині , а пару(, р) – класичним ймовірнісним простором. Якщо всі можливі результати випадкового випробування однаково ймовірнісні, то його ймовірнісна модель – це класичний ймовірнісний простір.

Подія в теорії ймовірностей – це будь-яка підмножина множини . Якщо пара(, р) – це класичний ймовірнісний простір і А – подія (тобто ), то Р(А), тобто ймовірність події А, дорівнює дробу.

Елементи множини А – це результати випробування, які сприяють події А. Останнє висловлювання стосовно Р(А) складає зміст так званої класичної теореми Лапласа. Його часто (і, на жаль, не правильно) вважають означенням ймовірності події. Далі ми будемо посилатися на нього як на теорему теорії ймовірностей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 2 Випадкова величина та ймовірнісний простір,який вона утворює на числовій осі

2.1. Результат випадкових випробувань.

 Виграш гравця у багатьох випадкових іграх залежить від того, яким результатом закінчиться випадкове випробовування, яке проводиться в цій грі. Виграш залежить від випадку.

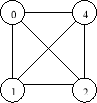
Випадково обираємо дві кулі зі скриньки, в якій чотири кулі, що позначені числами 0, 1, 2 і 4. Результат такого випробовування ми можемо тлумачити як двоелементну підмножину множини {0, 1, 2, 4}. Результат {j, k} позначимо через j-k. Маємо 6 можливих результатів На мал. 1 кожен результат зображено відрізком, який з’єднує два числа. Всі результати однаково ймовірні. Їх множина – це

= {0 – 1, 0 – 2, 0 – 4, 1 – 2, 1 – 4, 2 – 4}.

Функція р, для якої для кожного , є розподілом ймовірностей на множині . Пара (, р) є ймовірнісною моделлю випадкового випробовування, що розглядається.

Кожному результату зіставимо суму номерів обраних навмання двох куль. Таким чином на множині ми визначили деяку функцію Х. У нас Х(0 – 2) = 2, Х (2 – 4) – 6 Х (1 – 4) = 5 тощо.

Функція, яка кожному результату випадкового випробування ставить у відповідність число, називається випадковою величиною. Випадкову величину розглядатимемо в ймовірнісній моделі випадкового випробування, тобто в певному ймовірнісному просторі.

Через позначимо множину значень функції Х. Через {X = x} позначимо подію: {випадкова величина Х  набуває значення х}, для . Кожному значенню функції Х поставимо у відповідність ймовірність, з якою випадкова величина Х набуває цього значення. Через Р(Х=k) позначимо ймовірність, з якою випадкова величина Х може набути значення k.

 

 

2.2. Функція X – випадкова величина.

Функція Х, яка кожному результату випадкового вибору двох куль ставить у відповідність суму їх номерів, є випадковою величиною.

Розглянемо в цьому контексті таку проблему: потрібна гральна кістка, але вона кудись зникла. Що робити в цій ситуації?

Наведені раніше міркування підказують розв’язування цієї проблеми. У нас Р(Х = k) = для k = 1, 2, 3, 4, 5, 6. Гральну кістку можна «побудувати» з чотирьох куль, які позначені числами 0, 1, 2 і 4. Суму номерів двох навмання обраних куль можна інтерпретувати як число очок, що випали.

Кидаємо дві гральні кістки. Нехай одна з них біла, друга – чорна. Результат цього випадкового випробовування ми можемо зобразити у вигляді пари (х, у), де х – кількість очок, які випали на білій, у – кількість очок, що випали на чорній кістці. Пару (х, у) ми можемо зобразити у вигляді точки на площині. В такій інтерпретації множину всіх можливих результатів даного випробування зображає малюнок вище.

Пару (х, у) ми можемо тлумачити як число 10х+у. Наприклад пару (2, 3) ми запишемо як число 23. В такій інтерпретації множину зображає малюнок.

11	12	13	14	15	16
21	22	23	24	25	26
31	32	33	34	35	36
41	42	43	44	45	46
51	52	53	54	55	56
61	62	63	64	65	66

 

Усі результати кидання двох кісток однаково ймовірні. Ймовірність кожного дорівнює . На множині ми визначили, таким чином, функцію р, яка кожному результату кидання кісток ставить у відповідність ймовірність того, що саме ним закінчиться це кидання. У нас рдля кожного .Пара - це згідно з наведеним означенням, ймовірнісний простір. Він є моделлю кидання двох кісток.

Коли відбувається ця гра, то кидаєш дві кістки і отримаєш стільки очок, скільки їх випало. До кидання кісток твій виграш «в руках випадку». Цей виграш, з точки зору математики, є в такій ситуації функцією, яка кожному з можливих результатів кидання кісток ставить у відповідність суму очок, що випали. Ця функція визначена, таким чином, на множині всіх результатів кидання, тобто це випадкова величина. Позначимо її через Х.

У нас = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Нехай . Ймовірність, з якою випадкова величина Х може набути значення k. Наприклад, маємо чотири результатами кидання, для яких випадкова величина Х набуває значення 5, отже, Р (Х=5)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 3 Процес прийняття рішення в умовах ризику і в Ситуації невизначеності

3.1. Людська діяльність – процес з математичної точки зору

Людська діяльність – це неперервний процес прийняття рішень в обставинах ризику або невизначеності відносно стану навколишнього світу. Поглянемо на цей процес з математичної точки зору.

Ми говоримо про процес прийняття рішення, коли маємо справу не менш ніж з двоелементною множиною D можливих рішень. Нехай D = {}.  Результатом прийняття даного рішення є вигода (іноді втрата), яка виражається числом. Ця вигода (втрата) залежить від прийнятого рішення та від того, що трапиться пізніше, після прийняття рішення. Будемо говорити тут про стани навколишнього світу. Людина приймає рішення в той час, коли стани навколишнього світу ще невідомі, і вона не може визначити, при якому рішенні вигода буде максимальною, отже, яке з можливих рішень оптимальне. Стани навколишнього світу визначає випадок, отже ці стани є результатами випадкового випробовування (явища). Нехай = {} – це множина можливих станів навколишнього світу визначають їх ймовірності.

Математика створює свої засоби для встановлення критеріїв оптимальності рішення в ситуаціях, коли стани навколишнього світу є результатами випадкового явища (випробовування), для якого ми можемо побудувати ймовірнісну модель.

Нехай - ймовірність того, що станом навколишнього світу буде для k = 1, 2,..., s.

Вигода – це функція W двох змінних, яка визначена на множині D x . Число - це вигода, яка відповідає рішенню в ситуації, коли в майбутньому навколишній світ опиниться в стані .

З процесом прийняття рішення має справу продавець (наприклад, газет, хліба, квітів, напоїв тощо). Він приймає рішення, наприклад, стосовно кількості щоденних газет, придбаних на даний день. Через позначимо рішення «придбаю і примірників даної газети», через - стан навколишнього світу: «k осіб купить цю газету». Продавець купує газети в редакції і платить а грн. За примірник, а продає їх по b грн. (b>a). Ті газети, що залишилися непроданими – це втрати, хоча їх можна продати як макулатуру. Нехай в такому випадку один примірник коштує с грн. (с<а). Прибуток продавця залежить від кількості примірників, придбаних продавцем, а також від кількості покупців, які придбають цю газету. Те, скільки осіб купить газету, залежить від випадку. Попит, про який йдеться,  - це стан навколишнього світу. Попит в даний день, а інакше, кількість покупців, є випадковою величиною (її значення – це стани навколишнього світу). В описаній ситуації ми можемо визначити її розподіл, оскільки ми не знаємо, скільки (та з якою ймовірністю) буде в даний день покупців. Ми маємо тут справу з процесом прийняття рішення в обставинах невизначеності відносно станів навколишнього світу.

На малюнку зображено 28 кісток класичного доміно. Вибір навмання однієї кістки є випадковим випробуванням з 28 однаково ймовірними результатами. Результат випробовування – кістка, яку вибрали. Для кожної кістки шанси однакові. Мал. 5 фактично зображує множину . Розподілом ймовірності на множині є функція р така, що до кожного .

Розглянемо гру, в якій із 28 кісток доміно випадково обирається одна. Але раніше, ніж відбудеться це випадкове випробування, потрібно відгадати, яка сума очок буде на цій кістці. Якщо це вдалось, гравець отримає очко. Чи слід брати участь у цій грі? Яке прийняти рішення в такій ситуації?

У цій ситуації кожному результату випадкового випробовування ставиться у відповідність число (це сума очок на кістці, яку вибрали). На множині ми визначаємо випадкову величину Х.

У нас = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.

Можливі суми очок на кістках доміно складають тут можливі значення величини Х.

Нехай означає рішення: гравець робить ставку на  число і.  Серед можливих рішень слід виділити оптимальне. Питання стосується процесу прийняття рішення в умовах ризику, оскільки можна визначити апріорі ймовірності значень величини Х.

Через {X = k} позначимо подію {сума очок на вибраній кістці доміно дорівнює k}, або подію {випадкова величина Х набуває значення k}. Через  Р(Х=k } будемо позначати ймовірність події {X = k}. Число P (X = k) – це ймовірність, з якою випадкова величина набуває значення k. Ймовірнісний простір (, р) класичний, отже, беручи до уваги класичну теорему дістанемо, що:

У нас:

 

 

 

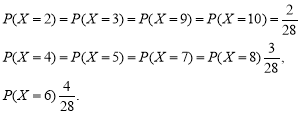
Для кожного значення випадкової величини Х ми знайшли ймовірність, з якою випадкова величина Х може набути це значення. На множині ми визначили таким чином функцією, яку позначимо через. У нас

k	0	1	2	3	4	5	6
	7	8	9	10	11	12

 

Зазначимо, що .Функція є розподілом ймовірності на множині - це імовірнісний простір, породжений випадковою величиною Х.

Через позначимо рішення: роблю ставку на число ,через - вигоду. Маємо = 1,коли i=k.

 При рішенні шанси отримати очко найбільші. Оптимальним рішенням є рішення .

У наведених ситуаціях гравець може отримати очко або ні.Вигода набуває тільки два значення: 0 або 1. Виникає тепер запитання: Як знайти оптимальне рішення в ситуації, коли вигода набуває не тільки значення 0 і 1?

 

3.2. Випадкова гра як модель процесу прийняття рішення в умовах ризику.

Розглянемо дії власника крамниці з товаром, який продається поштучно. Припустимо, що це товар, який швидко псується (квіти,фрукти, молоко в пакетах, напої) або товар, що зменшує свою вартість після деякого проміжку часу (булки, які можна на наступний день переробити на сухарі і продати, але дешевше, газети, які можна пізніше продати як макулатуру, але дешевше). Продавець щоденно замовляє цей товар у постачальника. Припустимо, що постачальник продає одиницю товару за a грн.., а в крамниці вона коштує b грн. і b > a. Прибуток продавця залежить від того, скільки одиниць товару він придбав (тобто від того, яке він прийняв рішення стосовно кількості одиниць товару, що слід придбати), а також від попиту, тобто від кількості покупців (припустимо що кожен покупець купує одну одиницю товару). Кількість покупців які прийдуть до крамниці у певний проміжок часу (наприклад, протягом дня) придбати одну одиницю товару, передбачити неможливо. Ця кількість випадкова. Невідома кількість покупців мовою теорії прийняття рішення є станом навколишнього світу. Розподіл цих станів визначити апріорі неможливо. Тут ми маємо справу з процесом прийняття рішення в умовах невизначеності, яка стосується станів навколишнього світу. З погляду математики ситуація продавця (залежно від типу товару) і процес прийняття рішення нагадують ситуацію гравця в деякій випадковій грі.
 Припустимо, що йдеться про продаж щоденної газети. Примірники, які не продали того дня, що розглядається, втрачають свою вартість, але їх можна продати на макулатуру за нижчу ціну. Продавець вирішує скільки примірників цієї газети слід придбати на даний день. У цей момент він не знає, скільки він матиме покупців. Це вирішує випадок. Кількість покупців є в даний момент випадковою величиною. Ми не в змозі знайти розподіл цієї випадкової величини, можна тільки визначити її можливі значення, але немає можливостей визначити, з якою ймовірністю ця величина набуває того або іншого значення. Така сама ситуація має місце і для продавця гамбургерів, він щоденно приймає рішення стосовно кількості булок, які варто купити для своєї закусочної. Тут ми не можемо засобами математики знайти оптимальне рішення оскільки ми не знаємо розподілу попиту.

Розглянемо таку гру.

 Біля входу в салон ігор можна купити будь яку кількість жетонів, один жетон коштує a грн. На цьому етапі гри стикаємося з необхідністю прийняти рішення стосовно кількості жетонів, які слід мати для гри. Гра полягає в киданні двох кісток доміно. У випадку, якщо гравець придбав i жетонів, а потім випало разом k очок, то:

якщо i ≤ k, тоді за кожний жетон каса салону сплачує гравцеві b грн., де b > a.
 якщо i > k, то за k жетонів сплачують по b грн. за жетон, а за інші по с

грн. за жетон, с < a. 

Виникає запитання: скільки жетонів варто купити біля входу? Питання стосується процесу прийняття рішення в умовах ризику. Рішення стосується кількості жетонів, які гравець купує біля входу. В цій ситуації сума очок, що випали під час кидання двох кісток, - це стани навколишнього світу. Можна визначити, з якою ймовірністю «навколишній світ» буде в тому чи іншому стані. Для кожної кількості придбаних жетонів можна знайти розподіл вигоди, яка відповідає прийнятому рішенню. Зазначимо, що ця гра добре відображає ситуацію продавця газет (один жетон – це один примірник газети). Ті газети, що не продали, - це жетони, за які отримають у грі по с грн. За жетон в ситуації, коли придбано жетонів більше, ніж потім випало очок. Ця гра імітує справжній процес прийняття рішення продавцем газет.

Виникає тепер запитання, яка гра імітує процес прийняття рішення в ситуації, коли товар, що продається, - це пакети молока.

Розглянемо ще таку задачу з теорії ймовірностей.

Необхідно розпалити багаття, але є тільки два сірники. Можна розпалити вогнище одним сірником, а якщо це не вдалося зробити, то використати другий сірник (рішення d₁), або обома сірниками одночасно (рішення d₂). Яке рішення оптимальне, якщо ймовірність розпалити вогнище одним сірником 0,7, а двома - 0,95?

Ця задача (це математична задача, хоча її сформулювали в нематематичних термінах) стосується процесу прийняття рішення в умовах ризику, оскільки відомі ймовірності станів навколишнього світу. Насправді ми цих ймовірностей не знаємо.

Фактично проблема, що розглядається, стосується процесу прийняття рішення в умовах невизначеності.

У наведеній вище задачі йдеться про два рішення: d₁ і d_2. З них кращим є те, при якому ймовірність того, що вогнище буде розпалено (подія А), буде більшою. Ймовірність події є в цій ситуації засобом прийняття рішення. Легко показати, що:

       - при рішенні d₁  P(A) = 0.7 + 0.7 – 0.7 * 0.7 = 0.91;

- при рішенні d₂ P(A) = 0.95.

З цих розрахунків випливає, що в даній ситуації рішення d₂ краще за рішення d₁.

Задача тільки з зовнішнього боку ілюструє процес застосування математики на практиці. Розв’язування задачі не охоплює фази математизації. Щоб розв’язування охоплювало також і цю фазу, розглянемо аналогічний процес прийняття рішення, який стосується раціональної участі у грі.
 В урні U₁ , є 7 чорних куль і 3 білі, в урні U₂ – 95 чорних куль і 5 білих. Необхідно з навмання вибраної урни витягти будь-яку чорну кулю. Можна витягати кулю з урни U₁ (рішення d₁), або з урни U₂ (рішення d₂), але якщо випадково витягуючи кулю з урни U₁ гравець потрапить на білу кулю, то можна цей вибір повторити (повертаючи кулю в урну). Яке варто прийняти рішення стосовно вибору урни?

Остання задача імітує проблеми з розпалюванням вогнища.

 

3.3. Математичне сподівання – прибуток салону азартних ігор
 Багато стохастичних проблем стосується організації азартних ігор, в тому числі і таких, в яких можна виграти гроші. Зрозуміло, що за участь в такій грі треба сплачувати. Прикладами таких випадкових ігор є спорт лото, гра в рулетку, а також російське лото. Такі ігри пропонують салони азартних ігор.

Розглянемо дуже просту випадкову гру. В скриньці U п’ять білих куль і одна чорна. Гравець навмання витягує дві кулі і за кожну вийняту білу кулю отримує 1 грн., за чорну – 10 грн. За участь в цій грі слід сплатити. При якій вартості цієї платні дана гра забезпечить прибуток власнику салону ігор.

Спробуємо розв’язати цю нематематичну проблему математичними засобами. Почнемо з фази математизації.
 Виграш гравця. Якщо його розглядати до випадкового вибору двох куль, є випадковою величиною W, яка набуває значення 2 і 11. Позначимо через x шукану платню за участь у грі. Відповідь x > 11, яку підказує інтуїція, не правильна. За такої платні ніхто не прийде грати (гра невигідна для гравця). Щоб знайти ймовірності, за якими випадкова величина W набуває своїх значень, треба побудувати ймовірнісний простір як модель випадкового вибору двох куль із скриньки U. Можливі два результати:

₀ : обидві вийняті кулі білі, ₁ : одна куля біла і дна чорна, отже, {_{0, 1}}

Ймовірність результату ₀ дорівнює , ймовірність результату ₁ дорівнює . Ймовірнісна модель випадкового вибору двох куль із скриньки U –пара  , де = {_{0, 1}};  p(₀) = ; p(₁) =;

Повернемося до випадкової величини W. Через { W = k } позначимо подію {випадкова величина  W набуває значення k },через P (W = k) – ймовірність цієї події. У нас { W = 2 } = {₀}, { W = 11} = {₁}, отже, P (W = 2) = p(₀) = ; P (W = 11) = p(₁) =.                            
 Ймовірність, з якою випадкова величина набуває значення a, тобто число P(W=a), будемо тлумачити як масу, яка зосереджена в точці а на числовій осі.
 

 

 

 

 

Чи приносить ця гра прибуток чи ні, можна говорити, підраховуючи гроші в касі салону після того, як у грі візьме участь багато гравців. Оцінимо прибуток салону після того, як у грі візьме участь, наприклад, 300 гравців. Розглянемо ситуацію, в якій один гравець візьме участь в цій грі 300 разів. Це теоретичний аналіз. Гравець покладе в касу салону 300x грн. Це прибуток салону. Оцінимо витрати, які може очікувати салон. Ймовірність отримати виграш, що дорівнює 2, дорівнює, отже з 300 ігор можна очікувати в середньому 200 ігор, в кожній з яких салон повинен буде сплатити 2 грн. Очікувані втрати складають грн. Ймовірність отримати виграш, що дорівнює 11 грн., дорівнює , отже можна очікувати, що приблизно в 100 іграх гравець отримає 11 грн. за кожну. Втрати, які можна очікувати від цих ігор, дорівнюють, таким чином, 2  200 +грн. Одночасно це очікуваний виграш гравця в цих 300 іграх.
 Гра, що розглядається. Принесе прибуток (тобто салон процвітатиме), якщо

 Права частина в останній нерівності – це очікуваний виграш гравця в одній грі.

Звернемо увагу на те, що:

 Остання сума – це очікуваний виграш гравця в одній грі. Він дорівнює 5 грн. Власник салону ігор може очікувати зиск, якщо x > 5 грн. Якщо платня за вхід дорівнюватиме 6 грн., то в середньому від кожного гравця 1 грн. залишиться в касі салону. Якщо в грі візьме участь 300 гравців, то салон може очікувати 300 грн. прибутку.
 Якщо платня за вхід дорівнює 5 грн., то очікується порожня каса. В такому випадку гру вважають несправедливою.
 Сума 2 P(W=2) + 11 P(W = 11) – це очікуваний виграш. Цю суму називають в теорії ймовірностей математичним сподіванням випадкової величини W і позначають через E(W). У нас E(W)=2P(W=2) + 11 P(W = 11). Гра, в якій виграш гравця є випадковою величиною, і за участь в якій треба сплачувати, вважається справедливою, якщо платня за вхід дорівнює математичному сподіванню виграшу.
 

3.4. Випадкова гра як модель деяких життєвих процедур
 У 80-ті роки в Польщі всі купюри (банкноти) біли однакових розмірів, тобто, нерозрізнювані на дотик. Розглянемо таку проблемну ситуацію: громадянин G хоча придбати газету, яка коштує 5 злотих. У нього в кишені п’ять купюр (банкнот) по 1 злотому і одна купюра в 10 злотих. У нього в руках валізи, отже, його руки зайняті. Громадянин G запропонував продавцеві газет, щоб він узяв з його кишені дві вибрані навмання купюри як платню за згадану газету. Чи варто продавцеві погодитися з цією пропозицією?
 Пропозиція не є безглуздою, оскільки за газету яка коштує 5 злотих, продавець може отримати 11 злотих. Виникає питання: Яке рішення в даній ситуації доцільно прийняти продавцеві газет і як його обґрунтувати засобами математики?
 Проаналізуємо ситуацію продавця. Фактично громадянин G запросив його до гри. За участь у грі громадянин вимагає платню 5 злотих (це ціна газети). Сума, яку за цю газету отримає продавець, є немов «виграш» продавця за результат випадкового вибору двох банкнот. «Виграш» продавця – це випадкова величина W. Оскільки E(W) = 5, то ця гра справедлива. Пропозицію громадянина можна вважати справедливою.
 Цей (дещо вигаданий, штучний) приклад вказує гру як модель деякої позаметематичної ситуації.
 Ось інша життєва подібна ситуація. Деякий товар (наприклад, фрукти, овочі, яйця) продають поштучно, хоча вартість різних екземплярів неоднакова. Зважувати і оцінювати вартість кожного окремо не зручно. Маса одиниці товару, яку вибрали навчання (якщо про неї говорити до покупки), є випадковою величиною. Позначимо її через W. Щоб товар продавати справедливо, потрібно встановити ціну одного екземпляру так, щоб отримана під час продажу сума дорівнювала справжній вартості всіх екземплярів. Спробуємо уточнити, як ця сума пов’язана зі згаданою випадковою величиною W.
 Якщо кількість усіх екземплярів дорівнює s, ціна одного кілограма дорівнює z грн., а маса всіх s екземплярів дорівнює c кг., то ціна одного екземпляра повинна складати грн. У наступній таблиці подані кількість і маса екземплярів товару, що є серед s екземплярів.

 

Маса	c1	c2	…	ck
Кількість екземплярів	s1	s2	…	sk

 

 Справжня вартість одного екземпляру масою в c₁ дорівнює. Вартість усіх екземплярів складає:
                                                 

Позначимо через m встановлену ціну одного екземпляра. Тоді

Зауважимо, що - це ймовірність того, що справжня вартість навмання вибраного екземпляра дорівнює , отже = P(W = ) для  і=1,2 …k.З цього випливає, що m = E(W).Таким чином, встановлена ціна одного екземпляра є математичним сподіванням випадкової величини W, яка випадково вибраному екземпляру ставить у відповідність його справжню вартість.
 Покупець одного екземпляра товару грає роль гравця, продавець – роль власника солону азартних ігор. Платня за участь у грі – це ціна одного екземпляру, виграш – це справжня вартість купленого екземпляра. Тут платня за участь у грі дорівнює математичному сподіванню виграшу. Отже, гра справедлива.
 

 

 

 

 

 

 

 

 

 

 

Висновки

 

У типових задачах з теорії ймовірностей часто потрібно обчислювати ймовірності «дивних» подій (наприклад, ймовірність того, що декілька осіб сідають так або інакше навколо круглого столу, або того, що неграмотна дитина складе з букв розрізаної азбуки правильне слово, або того, що мисливець застрелить зайця тощо). Виникають запитання: Хто і навіщо сформулював такі задачі? Хто потребує їх розв’язування?
 У цій роботі показано, що зміст задач з теорії ймовірностей може стосуватися навколишнього світу і що розв’язування цих задач може бути ілюстрацією справжнього процесу застосування математики. В роботі показано, як стратегічно-випадкова гра імітує (а тим самим моделює) реальні ситуації, з якими має справу учень у своєму повсякденному житті.
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

 

1. Бродський. Я. С. О прикладной направлености изучения вероятности и статистики в школе, Prace z Rachunku Prawdopodobie i jego Dydaktyki, Rocznik Naukowo-Dydaktyczny WSP, Zcszyt 191, Krakow 1997.
2. Плоцки. А. Вероятность в задачах для школьников, - М.:Просвещение, 1996.
3. Плоцки. А. Вероятность события в стохастической линии школьного математичиского образованиия//Математика в школе. – 1997. №2 (март –апрель 1997)
4. Плоцки. А. Стохастика в математике для всех. – Wydawnictwo Naukove WSP.: Krakow 1991.
5. Plocki. A. Propedeutyka rachunku prawdopodobienstwa i statystyki matrmatycznej dla nauczycieli, PWN, Warszawa, 1992/