Науково-дослідницька робота МАН "ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ"
1
Міністерство освіти і науки України
Департамент освіти і науки Івано-Франківської облдержадміністрації
Івано-Франківське обласне відділення Малої академії наук України
Відділення математики
Секція : математика
Дослідження функцій та побудова їх графіків
Роботу виконав:
Чаплінський Віталій Андрійович
учень 10 класу
Тлумацької міської ради
Івано-Франківського району
Івано-Франківської області
Насадик Марія Ярославівна
учитель математики
Тлумацького ліцею №1
Тлумацької міської ради
Івано-Франківського району
Івано-Франківської області
2023
Івано-Франківське обласне відділення Малої академії наук України
 Анотація
Анотація
Чаплінський Віталій Андрійович, учень 10 класу Тлумацького ліцею №1
Івано-Франківського району
Івано-Франківської області
Науковий керівник : Насадик Марія Ярославівна, учитель математики , Тлумацького ліцею №1 , Тлумацької міської ради, Івано-Франківського району , Івано-Франківської області
ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ
Досліджено загальний геометричний спосіб побудови графіків суми та добутку. Створено алгоритм виконання дій для нього. Цей спосіб дає можливість без обчислень кожній точці осі абсцис, що належить області визначення заданої функції, поставити у відповідність точку шуканого графіка.
У додатках упорядкований збірник завдань на побудову функцій, які можна виконувати та досліджувати , використовуючи даний метод.
Ключові слова: функція; область визначення; область значень; нулі функції; графік функції; асимптоти; монотонність.
ЗМІСТ
ВСТУП ……..………………………………………………………………….. 4
РОЗДІЛ 1
Основні відомості про функції………………………………………….......... 6
1.1. Історія виникнення функцій……………………………………………... 6
1.2 Загальні властивості функцій. Їх види…………………………………... 11
1.3.Перетворення графіків функцій………………………………………….. 13
РОЗДІЛ 2
Побудова графіків функцій………………………………………………….. 27
2.1. Побудова графіків функцій за допомогою послідовних перетворень
графіків елементарних функцій………………………………………………. 27
2.2.Побудова графіка суми функцій………………………………………….. 30
2.3.Побудова графіка добутку функцій……………………………………… 33
ВИСНОВОК……………………………………………………………………. 37
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ТА ЛІТЕРАТУРИ………………… 39
ДОДАТКИ……………………………………………………………………… 41
В С Т У П
У сучасній математиці та в різних сферах нашого життя використовується безліч функцій. Поняття функціональної залежності – одне з найважливіших понять сучасної математики. При дослідженні явищ та процесів природи, розв’язанні технічних задач, тощо зустрічаються факти, коли одна величина змінюється зі зміною іншої. Серед різних способів задання функції значного поширення набув графічний спосіб. Іноді графік становить єдино можливий спосіб задання функції.
Актуальність роботи полягає у тому, що завдання пов’язані з дослідженням функцій та побудовою їх графіків часто даються на різноманітних математичних конкурсах, а також зустрічаються в завданнях ЗНО. Слід відмітити, що результати зовнішнього оцінювання показали, що випускники мають труднощі при розв′язуванні завдань де зустрічаються функції. Тому я і обрав дану тему для повторення і поглибленого вивчення матеріалу.
Вміння будувати графіки функцій та їх читати, визначати проміжки монотонності, екстремальні значення та інші характеристики функцій за графіком – важливий момент математичної культури. Ці вміння необхідні майбутньому техніку, економісту, інженеру, лікарю. В багатьох задачах графік є лише допоміжним елементом розв′язку. Звідси і виникає необхідність володіти простими способами побудови графіків функцій.
Мета дослідження: встановлення способу побудови графіків суми та добутку функцій, графіка складеної функції без використання методів вищої математики. Нашим завданням – показати різноманітність підходів до побудови графіків , оскільки саме графіки є одним із найлегших і найдоступніших способів аналізу і прогнозування поведінки функції. Ці навички використовуються для розв′язування задач із фізики, економіки тощо.
Основні завдання дослідження:
- систематизація знань про графіки та властивості елементарних функцій;
- розширення знань про нестандартні методи побудови графіків функцій без використання похідних.
Об’єкт дослідження: теорія побудови графіків функцій.
Предмет дослідження: побудова графіків функцій за допомогою геометричних перетворень, побудова графіків суми та добутку функцій, графіка складеної функції.
Зв’язок даної роботи зі шкільною програмою.
Дана робота дуже тісно пов’язана зі шкільною програмою, адже функції вивчаються з 6 до 11 класу. Але графіки деяких функцій зі шкільних підручників з математики 10 -11 класу важко побудувати відомими раніше способами.
Наукова новизна дослідження.
У шкільному курсі середньої школи розглядається спосіб побудови графіків функцій за допомогою геометричних перетворень. У старшій школі ми досліджуємо і будуємо графіки функцій з використанням похідної. Але як відомо, краще розв'язати одну задачу декількома способами, чим декілька задач одним , тому ми досліджуємо нестандартні способи побудови графіків суми та добутку функцій, загальний геометричний спосіб побудови графіка складеної функції у=f(φ(х)).
Результатом дослідження є узагальнення та систематизація знань про графіки та властивості елементарних функцій; ознайомлення з одним із способів побудови графіків функцій без використання похідних – виконання арифметичних дій з графіками .
Практичне значення. Дана робота може використовуватись як для проведення факультативних занять з математики в 10 – 11 класах, так і для самостійної роботи учнів під керівництвом учителя з питань історії розвитку теорії функцій, побудови графіків функцій . Дослідження розвивають творчу активність учнів та формують в них потребупостійно розширювати та поглиблювати свої знання.
РОЗДІЛ 1
Основні відомості про функції
1.1. Історія виникнення функцій
Ідея функціональної залежності була висунута ще в давнину. Її зміст можна знайти вже в перших математично виражених співвідношеннях між величинами,у перших формулах для знаходження площі і об’єму фігур. Так, вавилонські вчені (4-5 тис. років тому), нехай несвідомо, встановили, що площа кола є функцією від його радіуса за допомогою знаходження грубо наближеної формули: S =![]() . Прикладами табличного завдання функції можуть служити астрономічні таблиці вавилонян, стародавніх греків та індійців.
. Прикладами табличного завдання функції можуть служити астрономічні таблиці вавилонян, стародавніх греків та індійців.
Починаючи з 17 століття, у зв'язку з проникненням в математику ідеї змінних, поняття функції застосовується явно і цілком свідомо. Шлях до появи поняття функції заклали французькі вчені Франсуа Вієт і Рене Декарт, вони розробили єдину буквену математичну символіку, яка незабаром отримала загальне визнання, в математику прийшла ідея зміннної. Тим самим з'явилася можливість записувати загальні формули. Крім того, у Декарта і Ферма в геометричних роботах з'являється чітке уявлення змінної величини і прямокутної системи координат. У своїй "Геометрії» в 1637 році Декарт дає поняття функції, як зміни ординати точки в залежності від зміни її абсциси; він систематично розглядав лише ті криві, які можна точно представити за допомогою рівнянь, притому переважно алгебраїчних.
У 1671 році Ньютон під функцією став розуміти змінну величину, що змінюється з часом (називав «флюент»). У «Геометрії» Декарта і роботах Ферма, Ньютона і Лейбніца поняття функції носило по суті інтуїтивний характер і було пов'язане або з геометричними, або з механічними уявленнями: ординати точок кривих - функція від абсцис (x); шлях і швидкість - функція від часу (t) і т.п. Саме слово «функція» (від латинського functio - виконання)вперше було вжито німецьким математиком Лейбніцем в 1673г. Починаючи з 1698 року, Лейбніц ввів також терміни «змінна» і «константа».
У 18 столітті з'являється новий погляд на функцію як на формулу, що зв'язує одну змінну з іншою. Це так звана аналітична точка зору на поняття функції. Підхід до такого визначення вперше зробив швейцарський математик Йоганн Бернуллі, який у 1718 році визначив функцію наступним чином: «функцією змінної величини називають кількість, утворених яким завгодно способом з цієї змінної величин і постійних». Для позначення довільній функції від x Бернуллі застосував знак (x), називаючи характеристикою функції.
Остаточне формулювання визначення функції з аналітичної точки зору зробив в 1748 році учень Бернуллі Ейлер: «Функція змінної кількості є аналітичний вираз, складений будь-яким чином з цієї кількості і чисел або постійних кількостей". Так розуміли функцію протягом майже всього 18 століття Даламбер, Лагранж, Фур'є та інші видатні математики .
Нові кроки у розвитку природознавства і математики викликали і подальше узагальнення поняття функції. У 1855 році Н.І. Лобачевський, розвиваючи вищезазначене ейлеровське визначення функції в 1755р., писав: «Загальне поняття вимагає, щоб функцією від x називати число, яке дається для кожного x і разом з x поступово змінюється. Значення функції може бути дано і аналітичним виразом або умовою, яка подає засіб відчувати всі числа і обирати одне з них, або, нарешті, залежність може існувати, або залишатися невідомою. Великий погляд теорії припускає існування залежності тільки в тому сенсі, щоб числа, одні з іншими в зв'язку, приймати як би даними разом ».
Сучасне визначення функції, вільне від згадки про аналітичне завдане, звичайно приписуване німецькому математику П.Л. Діріхле, неодноразово пропонувалося і до нього. У 1837 році Діріхле так сформулював загальне визначення поняття функції: «y є функція змінної x (на відрізкуaxb ), якщо кожному значенню x на цьому відрізку відповідає цілком певне значення y, причому байдуже, яким чином встановлено цю відповідність - аналітичною формулою , графіком, таблицею або навіть просто словами ».
У другій половині 19 століття після створення теорії множин в поняття функції, крім ідеї відповідності, була включена й ідея безлічі. При будь-якому геометричному перетворенні ми маємо справу з функцією. Іншими синонімами терміна «функція» у різних відділах математики є: відповідність, відображення, оператор, функціонал і ін. Подальший розвиток математичної науки в 19 столітті ґрунтувався на загальному визначенні функції Діріхле, яке стало класичним.
У загальному вигляді поняття узагальненої функції було введено французом Лораном Шварцем. У 1936 році 28-річний математик і механік С.Л. Соболєв першим розглянув окремий випадок узагальненої функції, що включає і дельта - функцію, і застосував створену теорію до розв'язання ряду задач математичної фізики. Важливий внесок у розвиток теорії узагальненої функції внесли учні та послідовники Шварца - І.М. Гельфант, Г.Є. Шилов та ін.
Важливою частиною вчення про функції є тригонометричні функції. Тригонометрія виникла і розвивалась в давнину як один з розділів астрономії, як її обчислювальний апарат, що відповідав практичним потребам людей. І саме астрономія визначила той факт, що сферична тригонометрія виникла раніше прямолінійної.
Для розвитку математики дуже важливими були праці індійських вчених з тригонометрії, хоч великих досягнень в цій галузі в них ще небагато. В зв’язку з розквітом астрономії в елліністичних країнах (пізніше провінціях Риму) були досягнуті значні успіхи в розробці як графічних засобів розв’язування її задач, так і обрахунку хорд. В “Аналемі” Птоломея були викладені графічні прийоми побудови для виготовлення сонячного годинника, тобто для встановлення місця положення Сонця в залежності від часу, прийоми, які також можна використовувати для визначення часу доби. В основі побудов лежало ортогональне проектування сфери на три взаємно перпендикулярні площини меридіана, горизонту і вертикального кола. Дуги, які шукались при цьому, будувались по півхордам відомих кіл. В „Аналемі” Птолемея міститься відносно розвинута тригонометрія хорд. Індійці спирались на праці елліністичних астрономів, але внесли і багато нового. Очевидно, що на розвиток астрономії в Індії вплинули більш ранні методи, які ввійшли в „Аналему”, і були перетворені тут в систему розрахункових правил. Головною була заміна хорд синусами. Така заміна сама по собі ніби й не помітна, адже хорда дуги r дорівнює подвоєному синусу дуги 2r, тобто відрізняється від синуса лише сталим множником. Але в дійсності перехід від хорди до півхорди мав важливе значення, тому що дозволив природно ввести різні функції, пов’язані зі сторонами і кутами прямокутного трикутника. В Індії було покладено початок тригонометрії, як вченню про тригонометричні величини, хоч і було відведено мало уваги саме розв’язанню трикутників. Синус і косинус також першими ввели індійські вчені. В Індії, по суті, і зароджується вчення про тригонометричні величини, яке пізніше було названо гоніометрією (“гоніа” – кут, “метрео” - вимірюю).
Подальший розвиток вчення про тригонометричні величини отримало в IX-XV століттях у країнах Середнього і Близького Сходу. Ал-Хабаш, Абу-л-Вафа, Ал-Баттані, ал-Біруні та інші вводять нові тригонометричні величини: тангенс, котангенс, секанс, косеканс, встановлюють основні співвідношення між ними, використовують їх під час різних обчислень.
Цікавим є той факт, що поняття “тангенс” і “котангенс”, як і перші таблиці цих величин, з’явились не внаслідок розгляду тригонометричного кола, а із вчення про сонячний годинник.
Тангенси (від латинського tanger - дотикатися) вперше було введено у десятому столітті, так як і котангенс, секанс і косеканс арабським математиком Абу–л–Вафою. Взагалі тангенси виникли у зв’язку з розв’язуванням задачі на визначення довжини тіні. Абу–л–Вафа першим склав таблиці для знаходження тангенсів і котангенсів. Але ці відкриття європейцям довгий час були невідомі, тому тангенси були наново відкриті в чотирнадцятому столітті спочатку англійським вченим Т. Бравердином, а потім ще й німецьким математиком, астрономом Регіомонтаном (1467 р.)Праця Регіомонтана “П’ять книг про трикутники всіх видів”(1462 - 1466), в якій тригонометрія розглядається як самостійний, незалежний від астрономії, розділ математики, була першою у Європі.
Зміст курсу тригонометрії складався до початку XVIII століття, але сучасна форма її викладу і загальноприйнята тепер символіка встановились лише з часів Ейлера, тобто в другій половині XVIII століття, зокрема, у 1748 році в його праці “Вступ до аналізу нескінченно малих”.Термін “тригонометричні функції” ввів німецький математик Г. Клюгель (1739 - 1812), який визначав тригонометричні функції, як відношення сторін трикутника.Сучасне позначення arcsin і arctg з’являються в 1772 році в працях віденського математика Шерфера і французького вченого Ж. Л. Лагранжа, але ще раніше дещо розглядав Д. Бернуллі. Символи arcsin і arctg стали загальноприйнятими в кінці вісімнадцятого століття (від латинського “арк” – лук, дуга).
Вперше графік тригонометричної функції, було зображено французьким математиком Ж. П. де Робервалем в кінці 30-х років XVII століття в зв’язку з визначенням площі циклоїди. Застосування графіків тригонометричних функцій набуло широкого розповсюдження лише після появи “Геометрії” Декарта і створення аналітичної геометрії. Проте вчені довгий час досліджували тригонометричні функції та будували їх графіки. Лише у 1670 році англійський математик Д. Вал ліс розібрався у питанні про знак синуса у кожному квадранті і побудував у своїй “Механіці” два повні оберти синусоїди, зазначивши, що їх нескінченна кількість .У 1668 році з’явились “геометричні етюди” англійського математика Д. Григорі, в яких вперше зустрічається частина тангенсоїди, що відповідає першому квадранту. В 1670 році були опубліковані “Геометричні лекції”
І. Барроу, в яких розміщені графіки косинуса, тангенса, секанса для першого квадранта (графіки останніх двох функцій виявилися неточними).
Питання про знаки тригонометричних функцій у всіх чотирьох квадрантах вперше було правильно викладено у 1705 році в мемуарах Паризької Академії наук Т. де Ланьї .
Тригонометрія довгий час розвивалась, як частина геометрії. Сьогодні тригонометрія розглядається як дисципліна, що вивчає тригонометричні функції та їх застосування. Застосування тригонометричних функцій відіграє важливу роль в геометрії, при вивченні комплексних чисел, при розв’язуванні рівнянь, при вивченні коливальних процесів, при вивченні функцій загального вигляду (наприклад, ряди Фур’є).
1.2 Загальні властивості функції та їх перетворення.
Розглянемо числові множини D та E, які складаються з елементів х та у відповідно. Тоді залежність змінної у від змінної х називають функцією, якщо
кожному значенню х Є D ми ставимо у відповідність єдине значення у ЄЕ. У математиці це записують таким чином : у = f(x).
У функції змінну х називають незалежною змінною або аргументом функції, змінну у – залежною змінною або значенням функції: символом f позначають правило ,за яким кожному у Є D можна знайти єдине відповідне йому значення у - Е. Для числових функцій(тобто для функцій, де множини D та Е числовими) під символом f розуміють ті операції, які потрібно виконати над аргументом, щоб дістати відповідне значення функції.
Множину D називають областю визначення функції у= f(х) і позначають D(f) або D(y),або D(f(x)). Таким чином, область визначення функції - це множина всіх значень , яких може набувати незалежна змінна.
Множину Е називають областю значень функції у=f(x) і позначають Е(f) або Е(у), або У(f(х)).
Парність. Графік парної функції симетричний відносно осі Оу. Графік непарної функції симетричний відносно початку координат. Тобто для побудови графіка парної або непарної функції треба побудувати графік для х Є [0;+∞), а тоді зробити відповідну симетрію. Багато функцій не є ані парними , ані непарними. Такі функції називаються функціями загального виду.
Перетин з осями. Оскільки ми розглядаємо побудову графіка функції, то перетинів із віссю у не може бути більше одного. Для того щоб знайти його координати підставляємо х=0 у нашу функцію, тобто перетин із віссю Оу – це точка (0;у0), де у0=f(0).
Перетинів із віссю Ох може бути як завгодно багато. Такі перетини називаються нулями функції, і всі вони є коренями f(x)=0, і навпаки, всі корені цього рівняння є нулями функції.
Проміжки знакосталості. Проміжками знакосталості називаються проміжки , на яких функція набуває додатних чи від’ємних значень. Такі проміжки є розв’язками відповідних нерівностей f(x)>0 або f(x)<0. На графіку такі проміжки відповідають частинам, які знаходяться вище або нижче за вісь абсцис.
Періодичність. Для того щоб побудувати графік періодичної функції , будують фрагмент графіка набудь-якому відрізку довжини Т(Т- головний найменший період). Потім здійснюють послідовні паралельні перенесення фрагмента графіка на Т,2Т,3Т іт.д. вздовж осі Ох(праворуч і ліворуч).
Нагадаємо ті перетворення функції у=f(x), які ми вміємо відображати графічно. Тобто ті перетворення, після яких ми можемо побудувати графік новоутвореної функції, виконавши відповідні перетворення графіка початкової функції.
- f(x) f(x+а). Графік функції у=f(x+а) утворюється паралельним перенесенням графіка функції у= f(x) уздовж осі Ох на а одиниць ліворуч, якщо а>0, і праворуч, якщо a<0.
- f(x) f(x)+в. Графік функції утворюється у= f(x)±в паралельним перенесенням графіка функції у= f(x) уздовж осі Оу на в одиниць угору, якщо в>0,і вниз, якщо в<0.
- f(x) f(kx), якщо k>0 . Графік функції у= f(kx) утворюється стиском графіка функції e= f(x) у k разів до осі Оу, якщо
-
k>1, і розтягом у
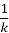 разів від осі Оу, якщо 0<k<1.
разів від осі Оу, якщо 0<k<1.
-
f(x) mf(x), якщо m>0. Графік функції y=mf(x) утворюється розтягом графіка функції y= f(x) у m разів від осі Ох, якщо m>1, і стиском у
 разів до осі Ох, якщо 0<m<1.
разів до осі Ох, якщо 0<m<1.
- f(x) f(-x). Графік функції y= f(-x) утворюється симетрією графіка функції y= f(x) відносно осі Оу. При цьому точки перетину графіка функції з віссю Оу залишаються незмінними.
- f(x) - f(x). Графік функції y=-f(x) утворюється симетрією графіка функції y= f(x) відносно осі Ох. При цьому точки перетину графіка функції з віссю Ох залишаються незмінними.
-
f(x)
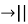 Графік функції утворюється із графіка функції таким чином: потрібно побудувати графік функції, потім відобразати симетрично відносно осі Ох частину графіка, нижчу від осі абсцис, і частину графіка, що нижча від осі абсцис, відкинути.
Графік функції утворюється із графіка функції таким чином: потрібно побудувати графік функції, потім відобразати симетрично відносно осі Ох частину графіка, нижчу від осі абсцис, і частину графіка, що нижча від осі абсцис, відкинути.
1.3 Основні види функцій та їх графіки
Лінійна функція:
1)у=b,де b- деяке число, наприклад
у=3 у=-3

Мал.1.1 Мал.1.2
2)у=kx, k≠0 наприклад
у=2х у=-5х;
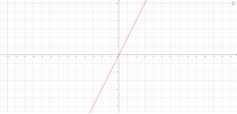
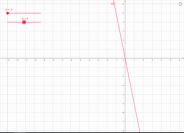
Мал.1.3 Мал.1.4
3)у=kx+b, b,k- дійсні числа , наприклад
у= 2х+5 у=-2х+5,
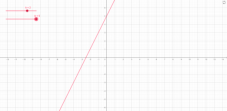
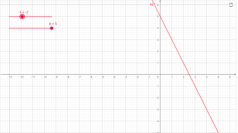
Мал.1.5 Мал.1.6
у=-2х-5, у=2х-5
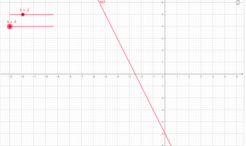
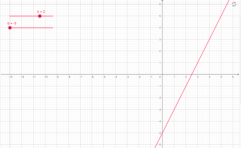
Мал.1.7 Мал.1.8
Обернена пропорційність:y=k/x, k≠0, наприклад
у=5/х у=-5/х.
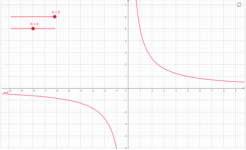
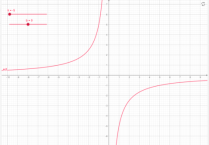
Мал.1.9 Мал.1.10
Квадратична функція. У=ах2+вх+с, де а,в,с- дійсні числа і а≠0. Наприклад
у=х2 у= -х2
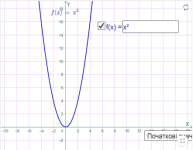
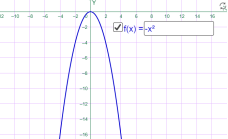
Мал.1.11 Мал.1.12
у=(х+2)2 у=(х-2)2
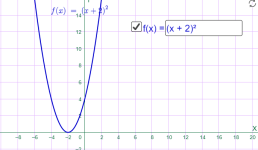
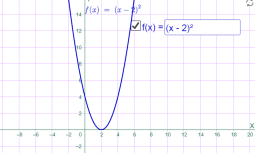
Мал.1.13 Мал.1.14
у=-(х+2)2 у=-(х-2)2
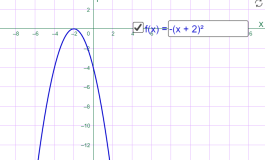
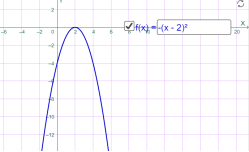
Мал.1.15 Мал.1.16
y=x2+2 y=x2-2 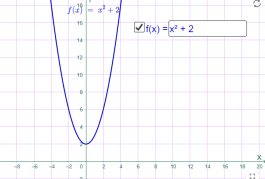
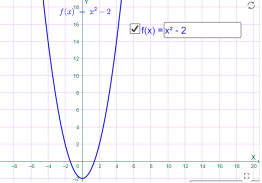
Мал.1.17 Мал.1.18
y=-x2+2 y=-x2-2
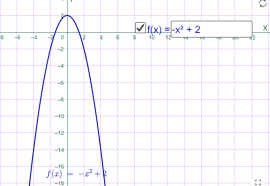
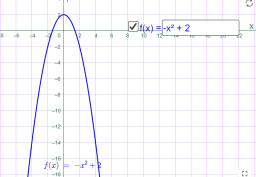
Мал.1.19 Мал.1.20
у=[x], де [x] – ціла частина числа х;
у={x}, де {x} – дробова частина числа х.
Степенева функція:1) у=хn, де n- натуральне число; Наприклад
у=х2 у=х3
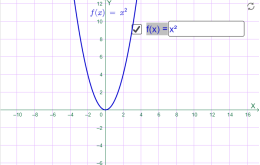
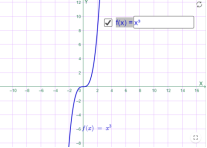
Мал.1.21 Мал.1.22
у=х4 у = -х2
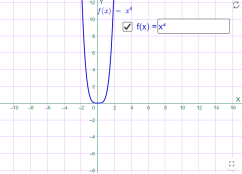
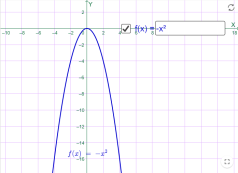
Мал.1.23 Мал.1.24
у=-х3 у=-х4
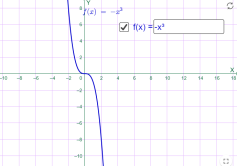
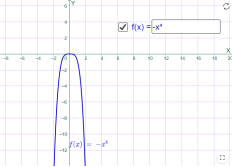
Мал.1.25 Мал.1.26
2)у=x-n, де n- натуральне число; Наприклад
у=х-2 у=х-3
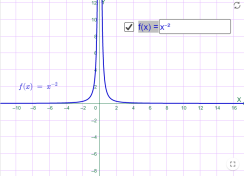
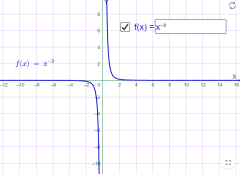
Мал.1.27 Мал.1.28
у=х-4 у=-х-2
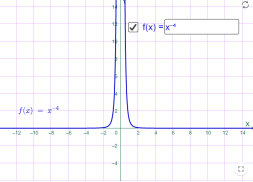
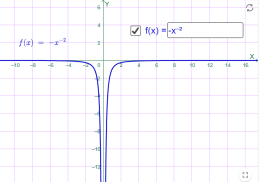
Мал.1.29 Мал.1.30
у=-х-3 у=-х-4
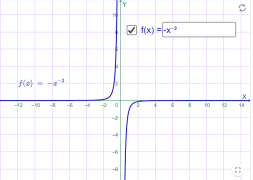
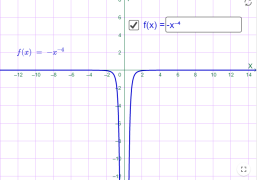
Мал.1.31 Мал.1.32
3)у = ![]() . Наприклад
. Наприклад
у=![]() у=
у=![]()
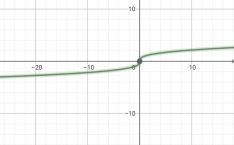
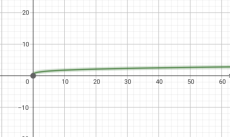
Мал.1.33 Мал.1.34
у=![]() у=
у=![]()
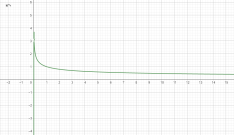
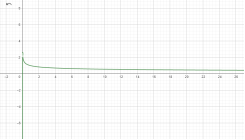
Мал.1.35 Мал.1.36
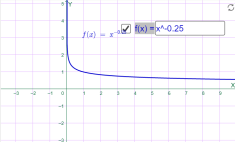
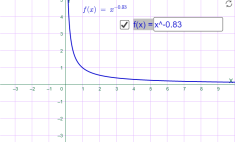
4)у=xr, де r- додатний нескоротний дріб; Наприклад
у=х0.25 у=х0.83
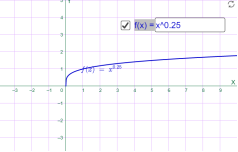
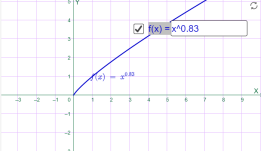
Мал.1.37 Мал.1.38
5)у=х-r, де r-додатний нескоротний дріб. Наприклад
у=х-0.25 у=х-0.83
Мал.1.39 Мал.1.40
Тригонометричні функції:
- у= sin x; Наприклад
у= sin x у= sin 2x
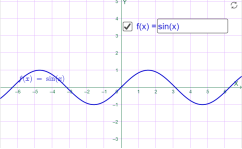
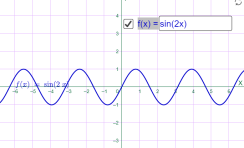
Мал.1.41 Мал.1.42
у= sin 0.5x у= sin (–x)
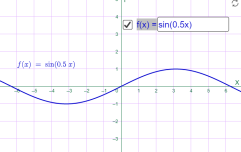
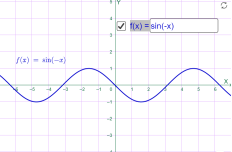
Мал.1.43 Мал.1.44
у= sin (-2x) у= sin(-0.5x)
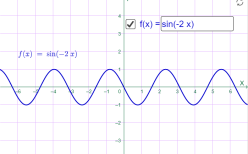
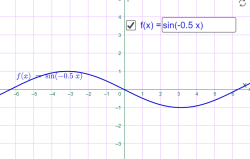
Мал.1.45 Мал.1.46
2)y=cos x; Наприклад
y=cos x y=cos 0.5x
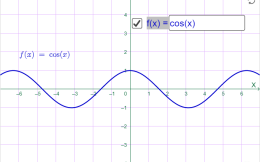
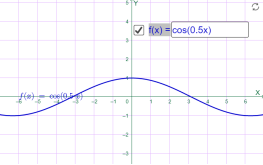
Мал.1.47 Мал.1.48
y=cos 2x
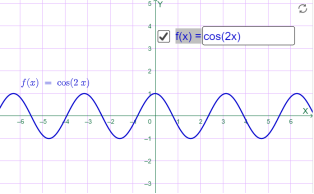
Мал.1.49
y=cos x та у= cos –x рівні.
3)у=tg x; Наприклад
у=tg x у=tg 0.5x
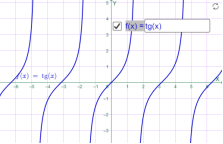
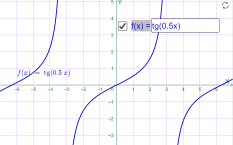
Мал.1.50 Мал.1.51
у=tg 2x у=tg (-x)
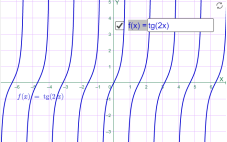
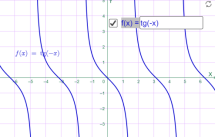
Мал.1.52 Мал.1.53
у=tg (-2x) у=tg (-0.5x)
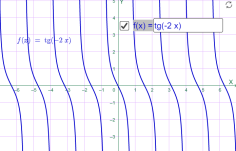
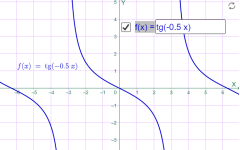
Мал.1.54 Мал.1.55
4) у=ctgx; Наприклад
у=сtg x у=сtg 0.5x
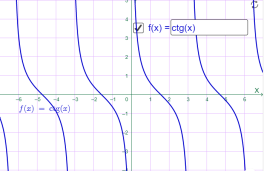
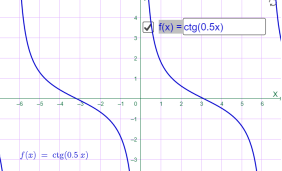
Мал.1.56 Мал.1.57
у=сtg 2x у=сtg (-x)
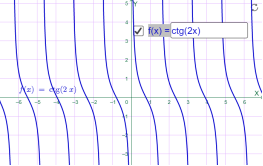
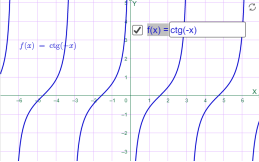
Мал.1.58 Мал.1.59
у=сtg (-0.5x) у=сtg (-2x)
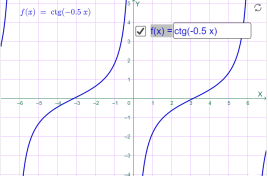
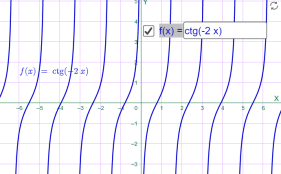
Мал.1.60 Мал.1.61
Обернені тригонометричні функції:
- у=arcsin x; Наприклад
у=arcsin x у=arcsin0.5х
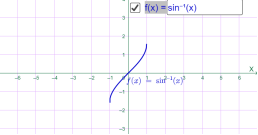
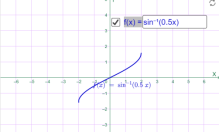
Мал.1.62 Мал.1.63
у=arcsin2x у=-arcsin х
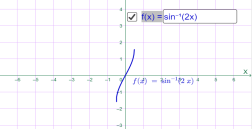
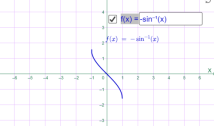
Мал.1.64 Мал.1.65
у=-arcsin0.5x у=-arcsin2х
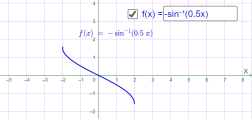
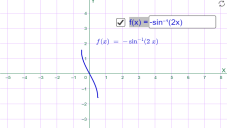
Мал.1.66 Мал.1.67
2)у=arccos x; Наприклад
у=arccos x у=arccos 0.5x
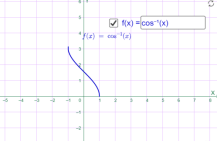
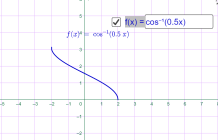
Мал.1.68 Мал.1.69
у=arccos 2x у=-arccos x
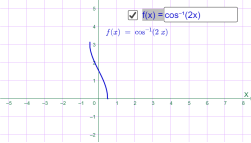
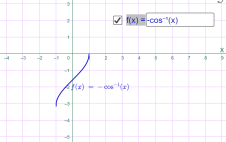
Мал.1.70 Мал.1.71
у=-arccos 0.5x у=-arccos 2x
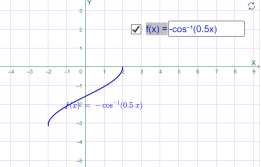
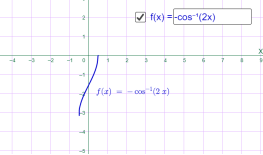
Мал.1.72 Мал.1.73
3)у=arctg x; Наприклад
у=arctg x у=arctg 0.5x
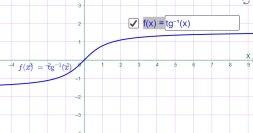
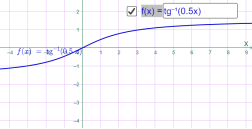
Мал.1.74 Мал.1.75
у=arctg 2x у=-arctg x
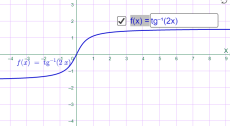
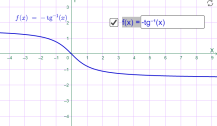
Мал.1.76 Мал.1.77
у=-arctg 0.5x у=-arctg 2x
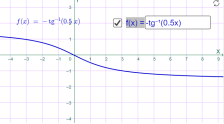
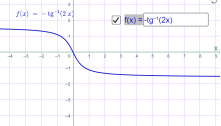
Мал.1.78 Мал.1.79
4)у=arcctg x; Наприклад
у=arcctg x у=arcctg0.5x
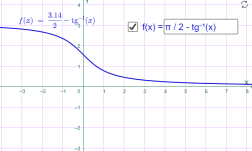
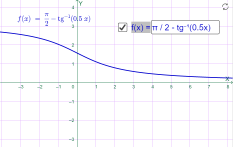
Мал.1.80 Мал.1.81
у=arcctg2x у=-arcctgx
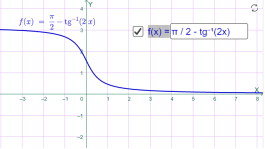
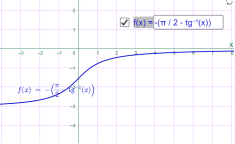
Мал.1.82 Мал.1.83
у=-arcctg0.5x у=-arcctg 2x
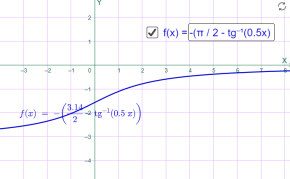
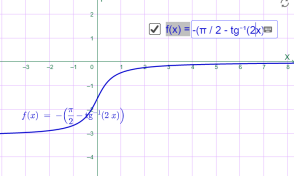
Мал.1.84 Мал.1.85
РОЗДІЛ 2
Побудова графіків функцій
2.1. Побудова графіків функцій за допомогою послідовних перетворень
графіків елементарних функцій
При побудові графіків функцій за допомогою послідовних перетворень з великою кількістю дій в рівнянні функції, складність викликає складання ланцюжка перетворень.
ПРИКЛАД 1 у=3sin(|x+![]() |)+4.
|)+4.
У праці розглядається алгоритм побудови графіків функцій за допомогою послідовних перетворень графіків елементарних функцій. Цей спосіб є легким для запам′ятовування, оскільки складається з чіткої послідовності нескладних дій. Запишемо його у вигляді ланцюжка.
1.У першу колонку записуємо за порядком дії, які необхідно виконати з числом, яке ми підставляємо замість х, для того щоб обчислити відповідне значення у:
2.Тепер вибираємо ту дію, яку неможливо відобразити перетвореннями графіка початкової функції. Це і буде наша стартова функція. Усе, що в таблиці розташовано вище стартової функції - це перетворення аргументу, а те, що нижче - функції.
3.Побудова ланцюжка завжди починається від стартової функції, тобто для аргументу ми пишемо дії «вгору»: спочатку найнижчу, потім вищу і так до першого рядка; а для функції – «вниз»: спочатку найвищу, потім нижче і так до
останнього рядка.
|
|
||
|
|x| |
||
|
sin x |
Стартова функція |
|
|
|
|
|
|
+4 |
||
Тобто наш ланцюжок перетворень буде виглядати так:
у=sinx→ у=sin|x|→ у=sin|x+![]() |→ 3sin|x+
|→ 3sin|x+![]() |→3sin|x+
|→3sin|x+![]() |+4.
|+4.
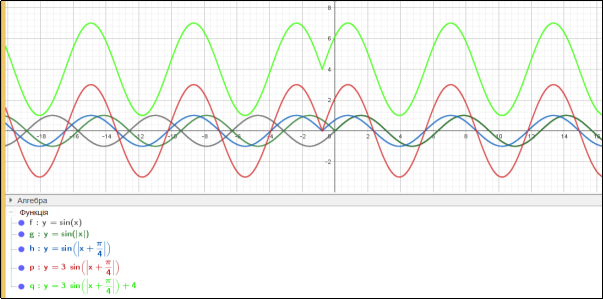
Мал.2.1
Зауваження. Перетворення для аргументу і функції незалежні, тобто не важливий порядок, в якому ми їх робимо (можливе спочатку перетворення аргументу, потім функції, а можливе навпаки). Проте не можна міняти порядок дій в одній групі (групі дій з аргументом або групі дій із функцією).
ПРИКЛАД 2 у=3arccos(2||x|-2|).
Робимо нашу табличку.
|
|x| |
аргумент |
|
Графік для х |
|
-2 |
Зсувграфіка на 2 праворуч |
||
|
|x| |
Графік для х |
||
|
|
Стиск графіка в 2 рази до осі Оу |
||
|
arccos x |
Стартова функція |
|
|
|
|
Функція
|
|
Розтяг графіка в 3 рази відосі Ох |
Ланцюжок перетворень:
у=arccosx→ у=arccos 2x→ у=arccos 2|x| → →у=arccos(2|x-2|) → у=arccos(2||x|-2|) → у=3arccos(2||x|-2|).
Подуємо графік функції.

Мал.2.2
2.2. Графік функції у=f(х)+φ(х)
Щоб побудувати графік функції у=f(х)+φ(х), спочатку доцільно побудувати графіки функцій – доданківу1=f(х), у2=φ(х), після чого значення функцій у1 і у2 для одного й того самого значення аргументу додати, тобто для фіксованого х0 дістанемо у0= f(х0)+φ(х0). Точка (х0;у0) належить шуканому графіку.
При цьому потрібно насамперед звернути увагу на характерні точки графіків функцій у1=f(х) і у2=φ(х) (екстремальні точки, точки перегину, точки перетину з осями координат таін.) і в цих точках обчислити значення функції у= f(х)+φ(х). Крім того слід врахувати парність, непарність, монотонність, періодичність функцій, що входять у суму, й будувати графік у спільній частині їх областей визначення.
Зауважимо, що в цей спосіб не варто будувати графіки виду
у=а1х2k+а2х2k-1+…+а2k+1, де а2,а3,…,а2k+1 – будь-які, а1![]() 0, оскільки неможливо цим методом визначити максимуми і мінімуми цієї функції.
0, оскільки неможливо цим методом визначити максимуми і мінімуми цієї функції.
ПРИКЛАД 3. у=2х3-0,5х+1.
Розв'язання. Побудуємо графіки функцій у1=2х3 та у2=-0,5х+1. Знайдемо відповідні значення функцій у1 і у2 в точках їх перетину з осями, точці перегину функції у1=2х3, а також у деяких додаткових точках, необхідних для побудови основного графіка заданої функції у=2х3-0,5х+1:
у1(0)=2![]() 03=0 у(0)=0+1=1;
03=0 у(0)=0+1=1;
у2(0)=-0,5![]() 0+1=1
0+1=1
у1(2)=2![]() 23=16 у(2)=16+0=16;
23=16 у(2)=16+0=16;
у2(2)=-0,5![]() 2+1=0
2+1=0
у1(1)=2![]() 13=2 у(1)=2+0,5=2,5;
13=2 у(1)=2+0,5=2,5;
у2(1)=-0,5![]() 1+1=0,5
1+1=0,5
у1(-1)=2![]() (-1)3=-2 у(-1)=-2+1,5=-0,5;
(-1)3=-2 у(-1)=-2+1,5=-0,5;
у2(-1)=-0,5![]() (-1)+1=1,5
(-1)+1=1,5
Наносимо на координатну площину отримані точки та з′єднуємо їх. Ескіз графіка функції у=2х3-0,5х+1 зображено
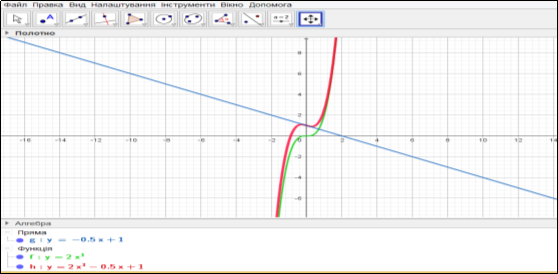
Мал.2.3
ПРИКЛАД 4 у=sinx-x.
Функція непарна, тому побудуємо графік спочатку для х![]() 0. Будуємо графіки у1=sinx і у2=x для х
0. Будуємо графіки у1=sinx і у2=x для х![]() 0.
0.
Урахувавши характерні точки синусоїди, обчислюємо значення функції
у=sinx-x у цих точках. Такими точками для sinx є точки (k![]() ;0),
;0), ![]() ,
, ![]() , де kЄZ.
, де kЄZ.
Скориставшись проміжками зростання (спадання) синуса, а також нанесеними контрольними точками, будуємо графік даної функції, симетрично відображаємо його відносно початку координат.

Мал.2.4
ПРИКЛАД 5 у=х-arcsinx.
Функція непарна, так як у(-х)=(-х)-arcsin(-x)= )=-х+arcsinx=
=-(х-arcsinx)=-у(х). Тому можна виконати побудову тільки для правої частин графіка (якщо х![]() 0).
0).
Будуємо графіки у1=x і у2=arcsinx. Ординати шуканого графіка знаходяться за допомогою різниці у1-у2. Характерні точки:
1) х=0, у1=0; у2=0; у= у1-у2=0-0=0; точка (0; 0);
2) х=1 (гранична точка) , у1=1; у2=arcsin1=![]() ; у= у1-у2=1-
; у= у1-у2=1-![]() -0,57;
-0,57;
точка (1; -0,57);
3) х=0,2 , у1=0,2; у2=arcsin0,2![]() 0,2; у= у1-у2=0,2-0,2
0,2; у= у1-у2=0,2-0,2![]() ;
;
точка (0,2; 0);
Ліву частину графіка будуємо симетрично відносно початку координат.
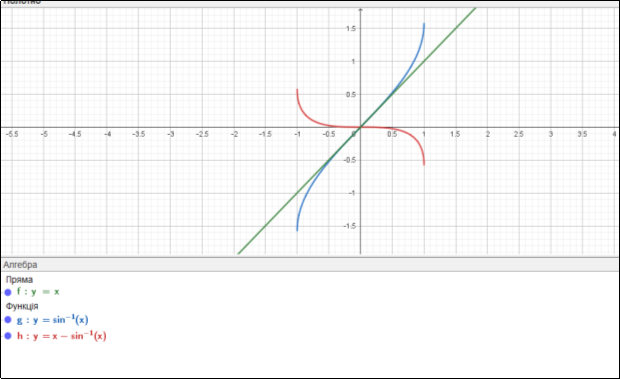
Мал.2.5
Приклад 6 ![]()
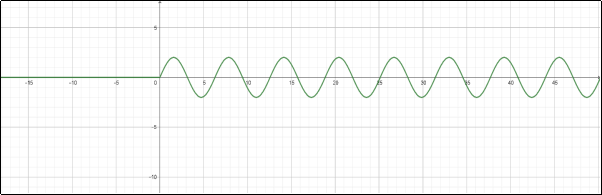
Мал.2.6
2.3. Графік функції у=f(х)![]() φ(х)
φ(х)
Щоб побудувати графік функції у=f(х)![]() φ(х) , можна провести спочатку загальне дослідження.
φ(х) , можна провести спочатку загальне дослідження.
Часто побудова графіка функції, що є добутком двох функцій, полегшується, якщо попередньо побудувати допоміжні графіки функцій-множників і відповідні ординати перемножити. Тут треба враховувати властивості функцій у1=f(х), у2=φ(х): парність, непарність, періодичність, монотонність, екстремальні точки тощо.
Функція у=![]() є часткою від ділення функцій у1=f(х) на у2=φ(х). Але для побудови графіка цієї функції зручніше розглянути її як добуток двох функцій у1=f(х) і у2=
є часткою від ділення функцій у1=f(х) на у2=φ(х). Але для побудови графіка цієї функції зручніше розглянути її як добуток двох функцій у1=f(х) і у2=![]() .
.
Будуються графіки функцій у1=f(х) і у2=![]() , відповідно ординати для характерних і контрольних точок перемножуються.
, відповідно ординати для характерних і контрольних точок перемножуються.
ПРИКЛАД 7 ![]()
Ця функція непарна, як добуток непарної функції на парну. Тому графік її буде симетричним початку координат.
Отже, достатньо його спочатку побудувати для х![]() Будуємо графіки функцій
Будуємо графіки функцій ![]() . Оскільки
. Оскільки ![]() набуває періодичного значення -1 доцільно побудувати ще допоміжну пряму
набуває періодичного значення -1 доцільно побудувати ще допоміжну пряму ![]() .
.
На цих проміжках, на яких ![]() мають різні знаки, шуканий графік буде розміщений у нижній півплощині ,а на тих проміжках ,на яких графіки набуватимуть одного знаку – у верхній півплощині.
мають різні знаки, шуканий графік буде розміщений у нижній півплощині ,а на тих проміжках ,на яких графіки набуватимуть одного знаку – у верхній півплощині.
Оскільки ,![]() то то
то то ![]() і отже ,графіки
і отже ,графіки![]()
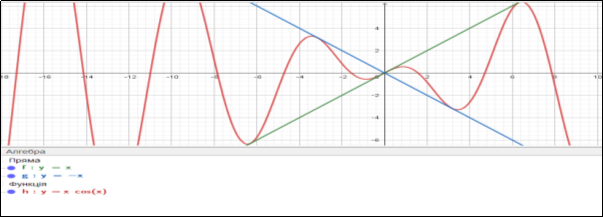
Мал 2.7
ПРИКЛАД 8 у=х![]() sinx.
sinx.
Будуємо графіки у1=x і у2= sinx. Множення цих графіків спрощується завдяки тому, що функція у2= sinx періодично приймає значення рівні 0 та 1. В першому випадку шуканий графік у=х![]() sinx перетинає вісь абсцис, в другому - дотикається допоміжної прямої у1=x.
sinx перетинає вісь абсцис, в другому - дотикається допоміжної прямої у1=x.
Так як функція у2= sinx періодично приймає значення рівне 0 і -1, то побудова графіка спрощується, якщо провести ще одну допоміжну пряму у3=-x.
Для всіх х=2![]() n-
n-![]() , nЄZ заданий графік дотикається до допоміжної прямої
, nЄZ заданий графік дотикається до допоміжної прямої
у3=-x, так як для цих значень х sinx=-1.
Так як задана функція у=х![]() sinx парна (у(-х)=(-х)
sinx парна (у(-х)=(-х)![]() sin(-x)=-х
sin(-x)=-х![]() (-sinx)=х
(-sinx)=х![]() sinx=
sinx=
=у(х)), то побудова проводиться тільки для правої частини графіка; ліва частина графіка будується симетрично правій відносно осі х.
1)х=0, у1=0; у2= sin0=0; у= у1![]() у2=0
у2=0![]() 1=0; точка (0; 0);
1=0; точка (0; 0);
2) х=1, у1=1; у2= sin1=0,84; у= у1![]() у2=1
у2=1![]() 0,84=0,84; точка (1; 0,84);
0,84=0,84; точка (1; 0,84);
3) х=3, у1=3; у2= sin3=0,14; у= у1![]() у2=3
у2=3![]() 0,14=0,42; точка (3; 0,42);
0,14=0,42; точка (3; 0,42);
4) х=4, у1=4; у2= sin4=-0,76; у= у1![]() у2=4
у2=4![]() (-0,76)=-3,04; точка (4; -3,04);
(-0,76)=-3,04; точка (4; -3,04);
5) х=5, у1=5; у2= sin5=-0,96; у= у1![]() у2=5
у2=5![]() (-0,96)=-4,8; точка (5; -4,8);
(-0,96)=-4,8; точка (5; -4,8);
6) х=7, у1=7; у2= sin7=0,66; у= у1![]() у2=7
у2=7![]() 0,66=4,62; точка (7; 4,62);
0,66=4,62; точка (7; 4,62);
7) х=8, у1=8; у2= sin8=0,99; у= у1![]() у2=8
у2=8![]() 0,99=7,92; точка (8; 0,99).
0,99=7,92; точка (8; 0,99).

Мал.2.8
ПРИКЛАД 9 ![]()
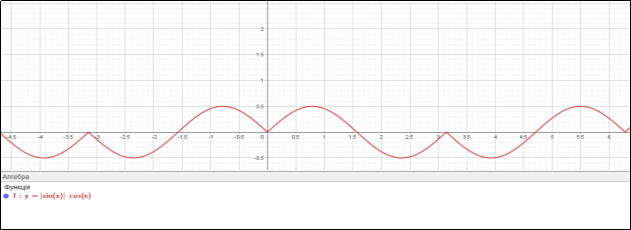
Мал 2.9
ВИСНОВКИ
Існує мова, яку розуміє кожна людина. Це мова графіків, схем та рисунків. «Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення» (К. Лебединцев). Дана наукова робота поглиблює функціональне мислення, сприяє покращенню навичок графічної культури та розвитку уяви .
В роботі систематизовано знання про історію, властивості і графіки елементарних функцій; проаналізовано і показано новий спосіб створення ланцюжка перетворень, який використовується при побудові графіків функцій за допомогою геометричних перетворень. Цей спосіб є легким для запам′ятовування, оскільки складається з чіткої послідовності нескладних дій. Особливу увагу звернено на метод побудови графіків суми та добутку функцій, наведено приклади з рисунками. Виявляється, що арифметичні дії можна виконувати не тільки з числами, змінними, виразами, а й з графіками функцій. При цьому графік даної функції суттєво змінюється, а значить змінюються властивості функції, які можна «прочитати» за графіком.
Провівши дослідження, ми навчилися будувати графіки функції геометричним способом. Алгоритм виконання даної побудови дається в літературі, а його практичне використання ми створили самостійно.
Також у додатках зібрано завдання різної складності на побудову функцій ,за допомогою методів ,показаних у даній роботі.
Дослідження показало, що розглянуті способи побудови графіків функцій:
- розвивають творчу активність учнів та формують в них потребу постійно розширювати та поглиблювати свої знання;
- розширюють математичну культуру учнів і демонструють наявність нетрадиційних підходів до розв’язування математичних задач;
- удосконалюють прийоми розумової діяльності учнів і розвивають в них дослідницький, творчий підхід до постановки і розв’язування задач при побудові графіків функцій.
Працюючи над роботою, я зрозумів, що дана тема є актуальною і перспективною в наш час. Вона може використовуватися на уроках математики, під час факультативних занять, при роботі математичних гуртків та буде цікава учням і вчителям, які люблять розв'язувати задачі нестандартними способами.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
- https://uk.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D1%84%D1%96%D0%BA_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D1%96%D1%97
- https://www.geogebra.org/m/z3MPvBNk
- Бевз Г. П. Алгебра і початки аналізу: підруч. для 10-11кл – 2-ге вид. / Г. П. Бевз. – Київ: «Освіта» 2006. – 255 с.: іл..
- Велика україномовна збірка учнівських видань [Електронний курс]. Розділ: Математика, алгебра, геометрія, статистика: www.ukrreferat.com – 674кб – Доступ до режиму:http://ukrreferat.com/index.php?referat=63306
- . Вишенський В. А. Збірник задач з математики: Навч. посібник. — 2-ге вид., доп. / В. А. Вишенський, М. О. Перестюк, А. М. Самойленко. — К.: Либідь, 1993. — 344 с.
- Гельфанд І.М. Функції і графіки (Базові приклади). – 6-те вид., перепрац. / І.М. Гельфанд, Е.Г. Глаголієва, Е.Е. Шноль. – М.: Москва «МЦНМО» 2004р. – 120стор.: ілюстроване.
- Гусак Г. М., Капуцкая Д. А. Математика для підготовчих окремих вузів: Справ. пособие / Под ред. А. А. Гусака. — М.: Высш. шк., 1989. — 495 с.
- Кремер Н. М. Математика для поступаючих у економічні вузи: Уч. пос. для вузов / Н. М. Кремер. — 2-ге изд., перероб. и доп. — М.: ЮНИТИ, 1998. — 43
- Маслова Т. Н., Суходений А. М. Ваш домашній репетитор / Т. Н. Маслова, А. М. Суходений. — М.: ОНИКС 21 век, 2003. — 672 с.
- Методи дослідження функцій [Електронний курс]: http://gov.cap.ru – 48кб – Доступ до режиму: http://gov.cap.ru/HOME/61/obraz/8/XLI/project/DswMedia/metodi kaissledovaniyfunkciypripostroeniigrafikov.
- Нелін Є. П. Алгебра і початки аналізу : підруч. для 10 кл. академ. рівень. / Є. П. Нелін. – Харків: Гімназія 2010. – 416 с. : іл.
- . Расіна Л.С., Расін І.Г., Карпов А.Н. Додаткові глави до шкільного курсу. Побудова графіків складних функцій. / Л.С. Расіна, І.Г. Расін, А.Н. Карпов. – Дніпропетровськ: НМОПИ «Альфа», 1997р. – 60 с.
- Розв’язання завдань онлайн [Електронний курс]. Розділ: Графіки: http://www.reshalki.ru – 83 кб – Доступ до режиму: http://www.reshalki.ru/yasam/graph.htm.
- Побудова графіків функцій елементарними методами. / А.Х. Шахмейстер. – Вид. 2-е, перепраць. – СПб.: Москва МЦНМО «ЧеРо-на-Неве» 2004р. – 184с.: іл.
ДОДАТКИ
2 Знаючи графік функції ![]() , побудувати графіки функцій
, побудувати графіки функцій
3 Знаючи графік функції ![]() , побудувати графіки функцій
, побудувати графіки функцій
8) ![]()
![]()
10) ![]()
![]()
![]()
![]()
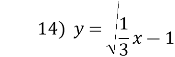
![]()


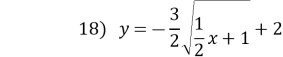
![]()
4 Знаючи графік функції![]() , побудувати графіки функцій
, побудувати графіки функцій
5 Знаючи графік функції ![]() , побудувати графіки функцій
, побудувати графіки функцій
6 Знаючи графік функцій ![]() ,побудувати графіки функцій
,побудувати графіки функцій
7 Знаючи графік функції ![]() ,побудувати графік функції
,побудувати графік функції
8 Знаючи графік функції ![]() побудувати графік функції
побудувати графік функції
![]()
9 Знаючи графік функцій ![]() , побудувати графік функції
, побудувати графік функції
10 Знаючи графік функції ![]() побудувати графіки функцій
побудувати графіки функцій
11 Знаючи графік функції ![]() ,побудувати графіки функції
,побудувати графіки функції
12 Побудувати графік функції
14 Побудуйте графік функції
15 Побудуйте графік функції


про публікацію авторської розробки
Додати розробку