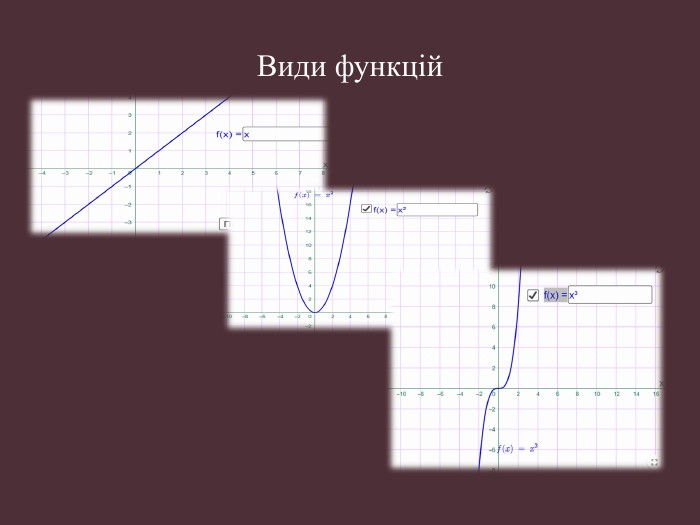
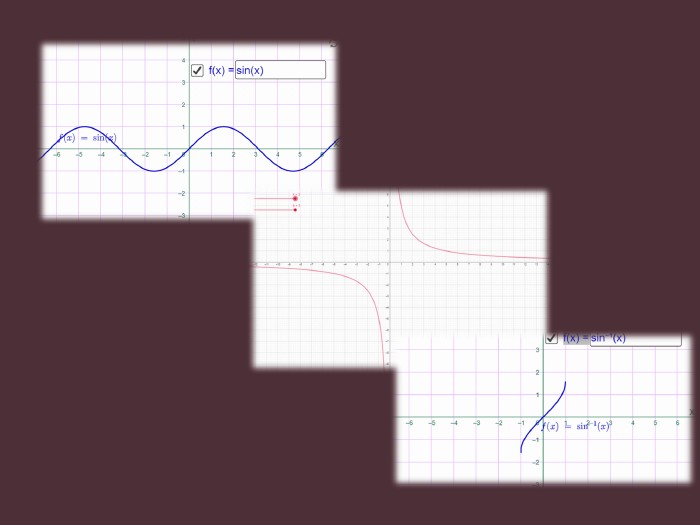
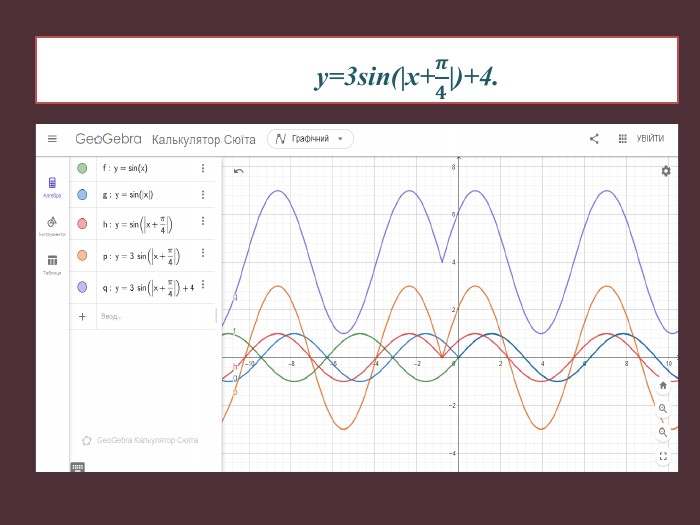
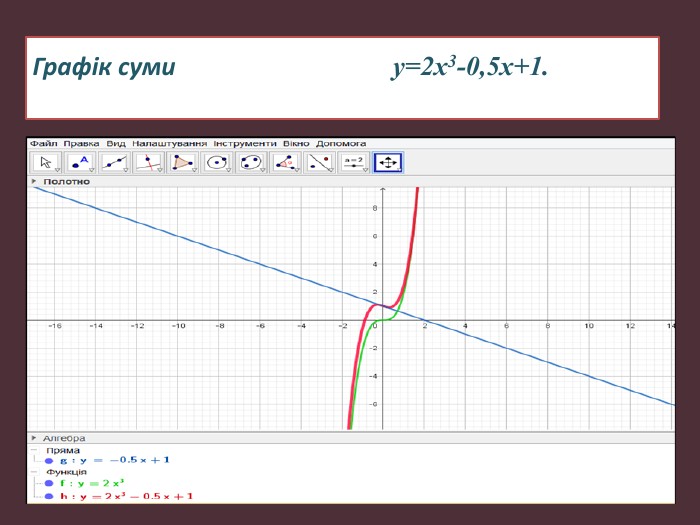
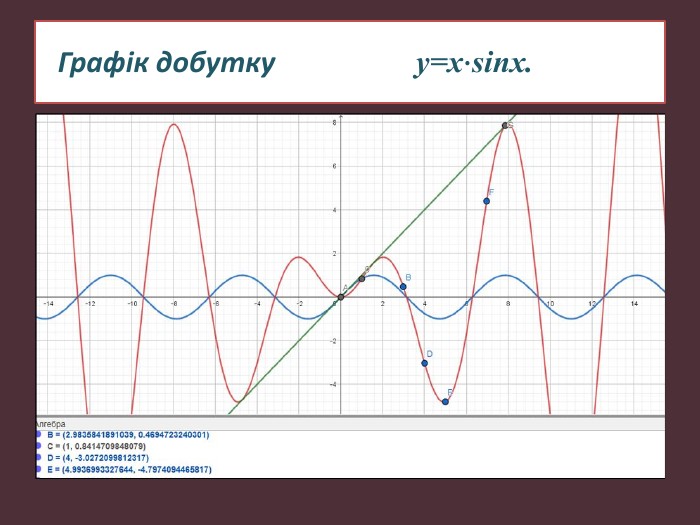
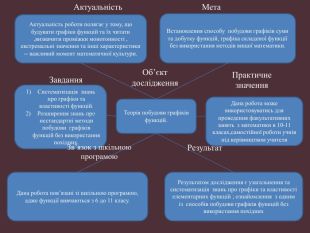
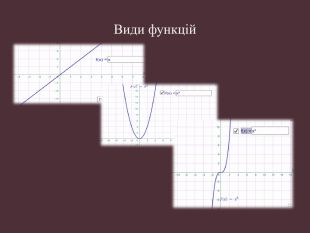
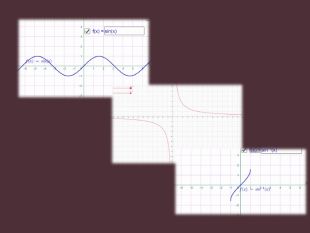
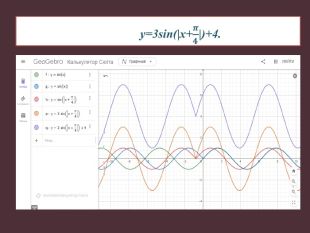
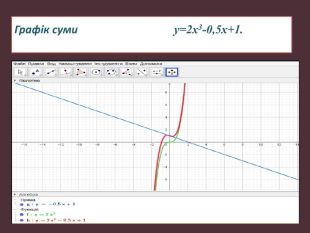
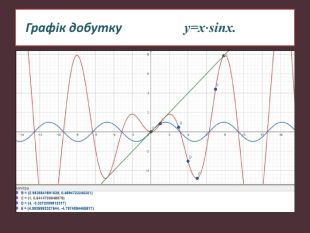
Науково-дослідницька робота МАН "ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ"
Про матеріал
Презентація для захисту науково-дослідницької роботи МАН "ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ" Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку