Проектні технології на уроках математики

Зачернецька гімназія

 

 

Проектні технології навчання

на уроках   математики

 

 

 

 

Богомазюк Олександр Михайлович,

вчитель математики

Зачернецької гімназії

 

 

 

 

      

 

 

 

 

                                                                    

                                                           

 

2022р.

 

 

Зміст матеріалів

1.Вступ…………………………………………………………………….3

2. Цілі навчання математики…………………………………………….4

3.Застосування комп’ютера на уроках математики ……………………5

4. Проектні технології в навчально-виховному процесі ……………....7

5 Розробка уроку математики в 8 класі на тему

   «Теорема Піфагора»……..………………………………………….....9

6.Висновки……………………………………………………………….18

7.Використана література……………………………………………….19

Додатки:

І. Учительська презентація на урок  ; 

ІІ. Учнівські роботи:        

•      Реферат
•      Публікація
•      Презентація
•      Веб-сторінка

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Вступ

«Усіма можливими способами треба запалювати в дітях палке прагнення до знань і до уміння. Пра­гнення до уміння збуджується... самими навчальни­ми предметами, методом навчання» — так говорив видатний чеський педагог Я. А. Каменський.

      Пріоритетним напрямом реформування освіти є досягнення якісно нового рівня у вивченні базового навчального предмета - математики. Ма­тематичні знання і вміння розглядаються не як са­моціль, а як засіб розвитку особистості школяра, за­безпечення його особистої грамотності, як здатність розуміти роль математики у світі, в якому він живе, висловлювати обґрунтовані математичні судження і використовувати математичні знання для задово­лення пізнавальних і практичних потреб. Відчути свою спроможність, успішність, комфортність на уроці дає використання сучасних технологій, а са­ме — проектної. Сучасна назва — проект, уже підви­щує інтерес учнів до вивчення математики.

     «Знання з теми повинні бути «цілісною сукупністю знань, які одне одного підтримують, зміцнюють і збагачують», «Вивчати сукупне ціле, а не щось спотворене, уривчасте або розірване», «Виклад по­винен бути повним, ґрунтовним і точним» — так го­ворив Я. А. Каменський. Досягнути цього дає мож­ливість використання цієї технології навчання. Метод проектів має велике значення для розвитку життєвої, соціальної, інформаційної, предметної компетентностей учня.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Цілі навчання математики

     Навчання математики в основній школі спрямоване на досягнення таких цілей:

•    формування в учнів математичних знань як невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві на основі ознайомлення школярів з ідеями і методами математики як універсальної мови науки і техніки, ефективного засобу моделювання і дослідження процесів і явищ навколишньої дійсності;
•    інтелектуальний розвиток учнів, розвиток їхнього логічного мислення, пам’яті, уваги, інтуїції, умінь аналізувати, класифікувати, узагальнювати, робити умовиводи за аналогією, діставати наслідки з даних передумов шляхом несуперечливих міркувань тощо;
•    опанування учнями системи математичних знань і вмінь, що є базою для реалізації зазначених цілей, а також необхідні у повсякденному житті й достатні для оволодіння іншими шкільними предметами та продовження навчання.

    Таким чином, математичні знання і вміння розглядаються не стільки як самоціль, а як засіб розвитку особистості школяра, забезпечення його математичної грамотності як здатності розуміти роль математики в світі, в якому він живе, висловлювати обґрунтовані математичні судження і використовувати математичні знання для задоволення пізнавальних і практичних потреб.

     Крім того, вивчення математики має сприяти формуванню в учнів загальнонавчальних умінь, культури мовлення, чіткості й точності думки, критичності мислення, здатності відчувати красу ідеї, методу розв’язання задачі або проблеми, таких людських якостей, як наполегливість, сила волі, здатність до переборення труднощів, чесність, працелюбство та ін.

     Незамінні можливості математики у вихованні алгоритмічної культури як здатності діяти за заданим алгоритмом, а також самостійно конструювати нові алгоритми на основі аналізу й узагальнення послідовності виконуваних операцій і дій, що ведуть до шуканого результату.

      Важливу роль у навчанні математики відіграє систематичне використання історичного матеріалу, який підвищує інтерес до вивчення математики, стимулює потяг до наукової творчості, пробуджує критичне ставлення до фактів, дає учням уявлення про математику як невід’ємну складову загальнолюдської культури. На дохідливих змістовних прикладах слід показувати учням, як розвивалися математичні поняття і відношення, теорії й методи. Ознайомлювати учнів з іменами та біографіями видатних учених, які створювали математику, зокрема видатних українських математиків, що сприятиме національному і патріотичному вихованню.

 

 

 

Застосування комп’ютера на уроках математики.

    Впровадження комп'ютерних технологій створює передумови для інтенсифікації освітнього процесу.

     Вони дозволяють широко використовувати на практиці психолого-педагогічні  розробки, що забезпечують перехід від механічного засвоєння знань до оволодіння умінням самостійно здобувати нові знання. Комп'ютерні технології сприяють розкриттю, збереженню і розвитку особових якостей навчання. Заняття дітей з комп'ютером включають чотири взаємозв'язані компоненти:

1.                     Активне пізнання дітьми навколишнього світу.
2.                     Поетапне засвоєння ігрових способів, що ускладнюються, і засобів  рішення ігрових завдань.
3.                     Зміна предметно-знакового середовища на екрані монітора.
4.                     Активізують спілкування дитини з дорослими і іншими дітьми.

      Інформаційні технології, в сукупності з правильно підібраними технологіями навчання, створюють необхідний рівень якості, варіативній диференціації і індивідуалізації навчання.

      При аналізі доцільності використання комп'ютера в навчальному процесі враховуються наступні дидактичні можливості комп'ютера :

•                    розширення можливості для самостійної творчої діяльності учнів особливо при дослідженні і систематизації навчального матеріалу;
•                    прищеплення навичок самоконтролю і самостійного виправлення  власних помилок;
•                    розвиток пізнавальних здібностей учнів;
•                    інтегроване навчання предмету;
•                    розвиток мотивації в учнів.

     При цьому  комп'ютер може представляти: джерело навчальної інформації; наочний посібник (якісно нового рівня з можливостями мультимедіа); тренажер; засіб діагностики і контролю.

    Проведення уроків з використанням інформаційних технологій - це потужний стимул в навчанні. За допомогою таких уроків активізуються психічні процеси учнів : сприйняття, увага, пам'ять, мислення; набагато активніше і швидше відбувається збудження пізнавального інтересу. Людина за своєю природою більше довіряє очам, і більше 80% інформації сприймається і запам'ятовується ним через зоровий аналізатор. Дидактичні достоїнства уроків з використанням інформаційних технологій - створення ефекту присутності ("Я це бачив"!), у учнів з'являється інтерес, бажання дізнатися і побачити більше.

     Практикую у своїй роботі для оптимізації освітнього процесу пояснення нового матеріалу з використанням комп'ютерної презентації як джерела навчальної інформації і наочного посібника.

   

     Мета застосування комп’ютера на уроках така:

•                     розширити межі творчої діяльності вчителя та учнів ;
•                     усвідомити можливості ефективного застосування комп’ютерних технологій;
•                     привчити учнів до самостійної дослідницької діяльності під час розв’язування практично спрямованих завдань.

      Комп’ютер також можна використовувати у навчальному процесі для підвищення його ефективності та розвитку в учнів загальноосвітніх  навичок , що ефективніше , ніж під час використання традиційних засобів.

     Комп’ютерні презентації Microsoft Power Point можна використовувати з різними  цілями та на різних етапах навчання :

•                     під час пояснення нової теми : урок проходить у вигляді шкільної лекції , де учні не тільки слухають, продивляються інформацію на екранах, конспектують, а й відповідають на запитання, розв’язують задачі за наведеним зразком.
•                     для контролю набутих теоретичних знань: презентація містить запитання з наступною появою правильної відповіді ( спочатку учень відповідає на запитання, а потім усі читають на екрані правильну відповідь).
•           - для індивідуальних завдань сильнішим учням : у позаурочний час учень, за бажанням , може підготувати( сам або з допомогою вчителя) презентацію на дану тему ( наприклад, довідку з історії розвитку математики, про вчених – математиків тощо) , а потім на уроці представити її іншим учням. Це спонукає учнів до пошуку потрібної інформації, а також сприяє розвитку творчого мислення, вміння правильно та стисло формулювати свої думки.

     Застосування комп'ютерної техніки дозволяє зробити заняття привабливим і по-справжньому сучасним, здійснювати індивідуалізацію навчання, об'єктивно і своєчасно проводити контроль і підведення підсумків.

     Таким чином використання комп'ютера на уроках - це не спосіб перекласти на плечі комп'ютера багатогранну творчу працю учителя, це вимога часу,  це виконання програм «100 відсотків» і «Відкритий світ»,  один із засобів, що дозволяє інтенсифікувати освітній процес, активізувати пізнавальну діяльність, збільшити ефективність уроку.

 

 

 

Проектні технології в навчально-виховному процесі.

У сучасних умовах, коли в школах впроваджуються інноваційні форми навчання, педагогам слід застосовувати форми взаємодії вчителя з учнем, що сприяють створенню умов для становлення дитини як творця і проектувальника свого життя.

Проектна діяльність дає можливість відійти  від стандартних традицій у навчанні, але вимагає інтегрування різноманітних засобів, форм, методів і прийомів навчання, формує та розвиває пізнавальну активність учнів, сприяє розвитку вмінь самостійно набувати знання, поєднувати їх у певну систему, використовувати в реальному житті.

Ефективність такої діяльності буде високою, якщо відбуватиметься за умови постійної, активної взаємодії всіх учнів і вчителя –керівника навчального проекту, який виступатиме в ролі лідера, турботливого наставника. Турбуюсь, наглядаю - латинською мовою означає «tucor» , англійською - «tutor» ,значить вчителю на певних етапах проекту слід проводити тьюторські заняття. За таких умов змінюється характер взаємодії вчителя та учня: наставник визначає  мету–  учень пропонує шляхи її сучасної реалізації; учень пізнає, вибирає, досліджує – вчитель підказує джерела знань; учень веде пошук, збір інформації – вчитель об’єктивно оцінює результати.

Спираючись на методичні рекомендації проектних технологій навчання з’ясували, що:

• вчитель і учень – повинен розуміти особливості проектної методики;
• визначити тему, мету, завдання проекту;
• активізувати роботу учнів, які мають певний достатньо -високий рівень навчальних досягнень чи проявляють практично – конструкторські здібності;
• бачити предмет дослідження, чітко визначивши принципи співпраці у певному напрямі діяльності;
• доводити розпочату роботу до завершення, презентуючи напрацювання на відкритому уроці.

Проаналізувавши програму і цілі розвитку  математики в 8 класі                                визначили тему навчального проекту «Роль Піфагора в розвитку математики». На засіданні ради математичного кабінету склали «Резюме проекту».

1. Тема навчального проекту «Роль Піфагора в розвитку математики».

2.Спрямованість проекту за ознаками : інформаційний, груповий, презентаційний.             

3. Виконавці проекту: учні 8 класу.

4. Мета проекту: створити атмосферу для відповідальної і відкритої взаємодії, що означає заохочення учнів задавати питання та шукати відповідь, відповідально співпрацювати з іншими для пошуку знань.

5. Завдання проекту:

- реалізація навчальних досягнень по темі;

-створити структуру заходів і форм діяльності, що дозволять розвинути процеси мислення, сформувати в учнів інтелектуальні вміння і мотивацію досягнення в навчанні і в житті.

6. Термін виконання 1 місяць.

7. Актуальність проекту: дослідження внеску Піфагора у становлення математики як науки.

8.

                                                                                                                                                                                    

9. Логічна послідовність етапів реалізації проекту:

10. Очікувані результати і вплив проекту на діяльність вчителів та учнів.

Даний проект сприяв активізації діяльності колективу і дирекції школи в напрямі застосування проектних технологій навчання; практична користь для випускників як майбутніх студентів.

     Отже, метод проектів дозволяє:

• перевірити та закріпити на практиці теоретичні знання;
• забезпечити продуктивний зв'язок теорії та прак­тики у процесі навчання;
• набути життєвого досвіду;
• розвивати вміння аналізувати, систематизувати, узагальнювати вивчений матеріал;

• здійснювати організовану пошукову, дослідни­цьку діяльність на підставі спільної праці учнів;
• навчити учнів самостійно працювати з додатко­вою літературою;
• вчити вміння самостійно працювати над творчи­ми завданнями;
• підвищувати інтерес учнів до вивчення математики;
• виховувати повагу, вміння працювати в колек­тиві;
• формувати власну життєву позицію.

Проектна діяльність для вчителів є однією з форм організації навчально-виховного процесу, розвитку компетентності, підвищення рівня якості освітніх послуг, демократичного стилю спілкування з дітьми.

 

 

 Тема уроку: Теорема Піфагора

 Мета уроку:

освітня : розкрити суть       теореми Піфагора, прищепити навички обчислення невідомої сторони прямокутного трикутника за двома відомими, навчити застосовувати теорему Піфагора до розв’язання найпростіших задач.

розвиваюча : сприяти розвитку здібностей до зіставляння, кмітливість, увагу, розвиток здібностей до аналітико-синтетичного мислення, розширення кругозору.

виховна : формувати потреби в знаннях, зацікавленість до математики.

 Обладнання уроку: комп’ютер, дошка, портрет Піфагора, плакати з усними вправами, малюнки до задач, проектор, презентація до уроку.

 Тип уроку: урок вивчення нового матеріалу

 Очікувані результати:

 засвоєння учнями теореми Піфагора і наслідків з неї;

 виробити уміння розв’язувати найпростіші задачі з теми;

 викликати інтерес до біографії Піфагора;

 навчити учнів робити власні висновки.

 

Хід уроку

І. Організаційний момент.

Вчитель: Світ, що нас оточує- це світ геометрії. Запрошую вас до його пізнання і нехай сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір. Я надіюся на нашу співпрацю, свідоме засвоєння матеріалу уроку, зацікавленість до продовження роботи над проектом.

 У кулачному бою на  58-й Олімпіаді, яка проходила в 548 році до н.е. брав участь один із давньогрецьких математиків. Переказують, що через малий зріст судді не хотіли допустити його до змагань.

 Можливо, - заперечив молодий вчений, - мій вигляд і не викликає у вас довіри, але я буду наносити удари з такою математичною точністю, що супротивникові стане жарко. Моя глибока віра в число – це моє життєве кредо.

 І він додержав свого слова – став чемпіоном з цього виду спорту і утримував цей титул ще на кількох олімпіадах.

 То ж нехай його слова: „ Тимчасова невдача краща від тимчасової удачі” стануть девізом уроку.

 

 ІІ. Актуалізація опорних знань та умінь.

 

1. Вправа „Мозковий штурм”:

• Як називаються елементи прямокутного трикутника?
• Що називається косинусом гострого кута прямокутного трикутника?
• Чи може у прямокутному трикутнику бути тупий кут?
• Дано кути, градусна міра яких різна. Які косинуси цих кутів за величиною?
• Чи залежить косинус кута від розмірів трикутника? Від розміщення трикутника на площині.

 

 

2. Усні вправи за плакатами:

Обчислити косинуси гострих кутів даних трикутників:

 

 

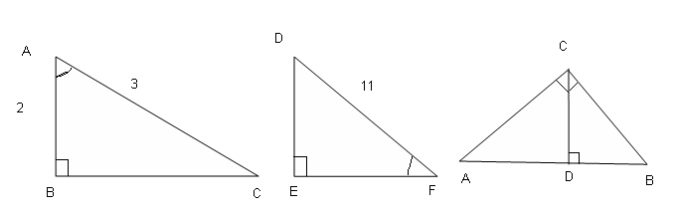
 3. математичний диктант:

- накресліть прямокутний трикутник із катетами 3 і 4 см;

- виміряйте гіпотенузу;

- знайдіть квадрати довжин усіх сторін;

- знайдіть суму квадратів катетів;

- порівняйте квадрат гіпотенузи із сумою квадратів катетів;

- зробіть висновок.

 

 ІІІ. Повідомлення теми, мети уроку, мотивація навчальної діяльності.

 

 ІV. Засвоєння нових знань.

1. Про Піфагора

          Піфагор — можливо найбільш знаменитий учений за всю історію людства. Він був не лише вченим і засновником першої наукової школи. Ця унікальна людина була і «володарем дум», проповідником власної «піфагорійської» етики, філософом, якого за силою впливу можна порівняти хіба що з його великими сучасниками. Піфагор виховав у людства віру в могутність розуму, переконаність у можливості пізнання природи, впевненість у тому, що ключем до таємниць світобудови є математика.

       Від мандрівників і капітанів кораблів він чув про близькі і далекі чудесні країни — Єгипет і Вавилон, мудрість жерців. Це дивувало молодого Піфагора і приваблювало. Зовсім юним він залишив батьківщину і вирушив до Єгипту, де 22 роки уважно придивлявся до навколишнього, прислухався до жерців. Як Піфагор потрапив у Вавилон, невідомо. Грандіозна панорама міста, що розкинуло свої палаци і високі оборонні стіни на обох берегах Євфрату, привела Піфагора в захват і здивування. Він швидко освоївся зі складними вавилонськими традиціями, у халдейських магів і жерців вивчав теорію чисел. І, може, саме звідси пішла числова містика приписування числам божественної сили, що була піднесена Піфагором як філософом. Легенди приписують Піфагору відвідання також Індії. Після повернення на Самос він намагався створити свою філософську школу. 3 невідомих причин Піфагор залишив Самос і оселився в Кротоні, де організував школу, яка діяла майже тридцять років. Школа, або як її ще називають — піфагорійський союз, складалася головним чином з аристократії. Це була одночасно і філософська школа, і політична партія, і релігійне братство. Наприкінці 5 ст. до н. е. в Греції і в більшості грецьких колоній прокотилася хвиля демократичного руху. Демократичні течії стали переважними й у Кротоні. Піфагор зі своїми прихильниками змушений був залишити Кротон. Він переїхав у Тарент, а звідти в Метапонт. Прибуття піфагорійців збіглося в часі з вибухом народного повстання. В одній з нічних сутичок і загинув майже дев'яностолітній Піфагор.

 

2. Формулювання теореми Піфагора.

Т е о р е м а. В прямокутному трикутнику квадрат    гіпотенузи дорівнює сумі квадратів катетів.

 

 Вчитель. Теорема – це твердження, яке доводять. Як говорив Леонардо да Вінчі: «Жодне людське дослідження не може називатись справжньою

наукою, якщо воно не пройшло через математичне доведення.

 

3. Доведення теореми

А зараз доведемо теорему Піфагора у сучасному формулюванні .

 

 

Накреслити трикутник АВС з прямим кутом С  .

 

 

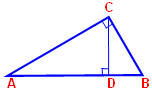
            Д а н о: Δ АВС, ∠ С = 90°.

 

Довести: АВ² = АС² + ВС².

 

Доведення

Проведемо висоту з вершини прямого кутаС.

Косинусом гострого кута прямокутного   трикутника   називається відношення прилеглого катета до гіпотенузи. Тому 

зΔ ACD   cos A = AD / AC,

а з  АВС   cos А = AC / AB.

 

Якщо рівні ліві частини цих рівностей , то рівні і праві їх частини ,тоді

 

AD / AC = AC / AB.

 

Звідси, виходячи із пропорції , отримаємо:

АС² = AD · АВ.

(1)

Аналогіно,

зΔ ВCD   cos В = BD / BC,

 

а  Δ АВС   cos В = BC / AB.

 

Так як рівні ліві частини цих рівностей , то рівні і праві їх частини ,тоді

BD / BC = BC / AB.

 

Звідси, виходячи із пропорції , отримаємо :

ВС² = ВD · АВ.

(2)

Складемо почленно рівності  (1) і (2),    винесемо спільний множник за дужки:

 

АС² + ВС² = AD · AB + BD · AB = AB · (AD + BD).

Так як

AD + BD = АВ,

тоді

АС² + ВС² = AB · AB = AB².

Отримаємо, що

АВ² = АС² + ВС².

 

  

4. Наслідки теореми Піфагора

• Якщо а,в- катети,с- гіпотенуза трикутника, то а<с, в<с;
• cos α<1;

 

 

V.Закріплення знань

 Розв’яжемо усно кілька задач за готовими малюнками

 

З а д а ч а №1

 

 

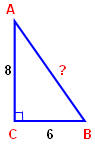
Розв’язання            

 

Δ АВС – прямокутний   з гипотенузою АВ,

за теоремою ПіфагораАВ² = АС² + ВС²,

 АВ² = 8² + 6²,

АВ² = 64 + 36,

АВ² = 100,

АВ = 10.

Результат:
АВ = 10

 

З а д а ч а №2

 

 

 

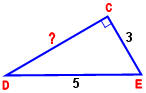
Розв’язання            

 

Δ DCE – прямокутний   з гипотенузою DE (рис. 16),

за теоремою Піфагора: DE² = DС² + CE²,

DC² = DE² – CE²,

DC² = 5² – 3²,

DC² = 25 – 9,

DC² = 16,

DC = 4.

Результат:
DC = 4

 

 

З а д а ч а №3

 

 

 

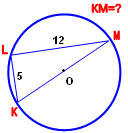
Розв’язання            

 

 

Δ KLM вписаний  в коло            і спирається на діаметр KM  . Так як вписані кути опираються на діаметр , - прямі, то кут  KLM – прямий. Значить, Δ KLM – прямокутний. За теоремою Піфагора для прямокутного трикутника  KLM з гипотенузою КМ:

KM² = KL² + KM²,

KM² = 5² + 12²,

KM² = 169,

KM = 13.

Результат:
KM = 13

 

 VI.Формування практичних умінь (використовується Погорєлов О.В. Геометрія: Планіметрія: Підручн. для 7 – 9 кл. загальноосвіт.навч.закл.- 8-ме вид. - К.: Школяр, 2004)

 1. № 2 (3)

 У прямокутному трикутнику дано катети а і в. Знайдіть гіпотенузу,  якщо  а = 5, в = 6.

  

 

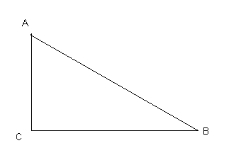
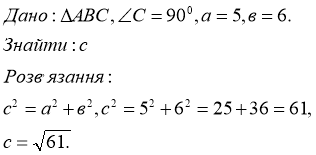
          2.№ 3 (2)

 У прямокутному трикутнику дано гіпотенузу с і катет а. Знайдіть другий катет, якщо с = 12, а =5.

 

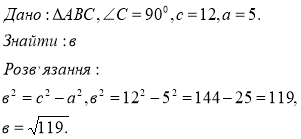
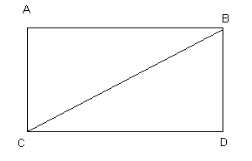
 3.Сторони прямокутника 8 см і 15 см. Знайдіть його діагональ.

 

 

 

 

 

 

 

 

 

 

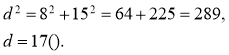
4.№ 6 (1)

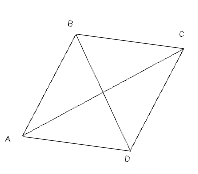
 Знайдіть сторону ромба, якщо його діагоналі дорівнюють 6 см і 8 см.

 

 

 

 

 

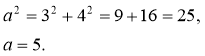
VIІ. Домашнє завдання: вивчити п. 63, повт. 62. № 2 (2), 3 (3)

  Додаткова задача (за бажанням учнів)

 На березі річки росла тополя висотою 15м. Буря зламала дерево на висоті 6 м від землі так, що вершина уперлась в інший берег. Знайдіть ширину річки СВ, якщо вважати, що АСВ = 90⁰.

     

         VІІI. Підсумки уроку.

 

1.Вправа „Мікрофон”.

Що нового  дізнались на уроці?

Як читається теорема Піфагора?

Які наслідки з теореми Піфагора?

Що корисного для себе ви винесли з уроку?

Де, у яких ситуаціях ви можете використати набутий на уроці досвід?

Що було потрібним на уроці зайвим?

Що ви очікували від уроку? чи збулися ваші очікування?

2.Усна вправа – знайдіть помилку – „Метод ПРЕС”.

 

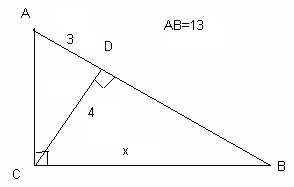
З ∆ DСА:  DА = 13-3 = 10,

                  Х² = 4² + 10² = 116

З  ∆ АВС:  ВС² = 16 + 9 = 25

                   Х² = 169 – 25 = 144

                   116 ≠ 144 

 

 

 

 

 

   

 

 

 

 

 

Висновки

Використання методу проектів дає змогу відповісти на низку запитань. Наприклад, як часто можна використовувати метод проектів у навчальній діяльності? Скільки часу потрібно для реалізації проекту? Яка форма презентації найвдаліша? Наскільки важлива підготовча робота?

Головна цінність проекту в тому, що придбає вчитель та учень, беручи участь у проекті. Тобто якість проектної діяльності залежить від сукупності зусиль вчителя та учня. А починається все з мотивації, тільки не учнів, а вчителя. Якщо сам викладач не має мотивації, то і в учнів її не може бути. Другим важливим чинником успішної проектної діяльності є рівень професійної майстерності та особисті риси вчителя-дослідника, вчителя – організатора, вчителя - партнера, вчителя-консультанта.

У роботі над проектом виявляється максимальна самостійність учнів у формуванні мети і завдань, пошуку необхідної інформації, навичок дослідницької діяльності, розвивається творчість.

Реалізація методу проектів на практиці змінює роль вчителя під час навчального процесу. Із носія готових знань він перетворюється на організатора пізнавальної діяльності учнів. Змінюється й психологічний клімат у колективі, оскільки вчителю необхідно переорієнтувати свою навчально-виховну роботу і роботу учнів на різноманітні види самостійної діяльності, на пріоритет діяльності дослідницького, пошукового, творчого характеру.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використана література:

 

1. Газета "Математика" № 17, 1996.
2. Геометрія, 7-9: підручник для загальноосвітніх шкіл   / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.               : Просвіта2002.
3. Глейзер Г.И. Исторія математики в школі. – М.: Просвіта, 1981.
4. Журнал "Математика в школі" № 4, 1991.
5. Литцман В. Теорема Пифагора. М., 1960.
6. Погорєлов А.В. Геометрія: Підручник. для 7-11 кл.  : Просвіта, 1995.
7. Чистяков В.Д. Старинные задачи по элементарной математике. Минск, 1978.
8. Энциклопедия для детей. Т.11. Математика / Глав. ред. М.Д. Аксёнова. – М.: Аванта+, 1998.
9. Я познаю мир: Детская энциклопедия: Математика. – М., 1997.
10. . Сучасні освітні технології. Навчальний посібник / Г.К. Селевко. - М.: Народна освіта, 1998. - 256 с.
11.  Ільясова, Р.А. Шляхи формування методичної майстерності майбутнього вчителя математики у використанні інформаційно-комунікаційних технологій / Р.А. Ільясова / / Інформатика та освіта. - 2009. - № 3. - С. 100-102.
12. Андрєєв, А.А. Комп'ютерні та телекомунікаційні технології в сфері освіти / А.А. Андрєєв / / Шкільні технології. - 2007. - № 3. - С. 151-170.
13.  Слєпкань З.І. Методика навчання математики. - К.: Зодіак - ЕКО, 2000.
14. Архіпова Т. Л. Вплив нових інформаційних технологій на активізацію навчально-пізнавальної діяльності підлітків / Т.Л. Архіпова. - С .160-167
15. Істер О.С. Збірник завдань для державної підсумкової атестації з математики. 9 клас / О.С. Істер, О.І. Глобін, О.В.  Комаренко. – Київ: Центр навчально-методичної літератури, 2011. – 114с.
16. Скляренко В.М., Іовлєва Т.В., Очкурова О.Ю. Видатні наукові відкриття
17. Роздатковий матеріал Історія розвитку математики
18. Технології конструювання мультимедійного уроку. – www.osvita.ua