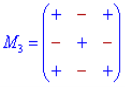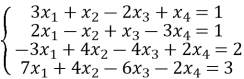Науково-дослідницька робота МАН "Розв’язування систем лінійних рівнянь методом Крамера"
1
Міністерство освіти і науки України
Департамент освіти і науки Івано-Франківської облдержадміністрації
Івано-Франківське обласне відділення Малої академії наук України
Відділення : математики
Секція : математика
Розв’язування систем лінійних рівнянь
методом Крамера
Роботу виконав:
Олійник Олег Ігорович
учень 10 класу
Тлумацької міської ради
Івано-Франківського району
Івано-Франківської області
Насадик Марія Ярославівна
учитель математики
Тлумацького ліцею №1
Тлумацької міської ради
Івано-Франківського району
Івано-Франківської області
2023
Івано-Франківське обласне відділення Малої академії наук України
Анотація
Олійник Олег Ігорович, учень 10 класу Тлумацького ліцею №1
Івано-Франківського району
Івано-Франківської області
Науковий керівник : Насадик Марія Ярославівна, учитель математики Тлумацького ліцею №1 , Тлумацької міської ради , Івано-Франківського району , Івано-Франківської області .
Розв’язування систем лінійних рівнянь
методом Крамера
Дослідницьку роботу присвячена одному з розділів сучасної математики «лінійна алгебра», який є цікавим та вартим уваги для вивчення. В ній звернено увагу, в першу чергу, на сутність поняття квадратної матриці, визначника та системи лінійних рівнянь з багатьма змінними; зроблено акцент саме на методі Крамера та приклади його застосування.
Досліджено історію вченого-математика Габрієля Крамера та його вплив на роль у галузі лінійної алгебри .
Проаналізовано умови існування розв’язків , показано застосування цих формул на конкретних прикладах. Останній підрозділ дослідницької роботи присвячений розв’язуванню однорідних систем лінійних рівнянь другого ,третього ,та четвертого порядків, наведено приклади. У додатку упорядкований збірник систем лінійних рівнянь, які можна розв’язувати , використовуючи даний метод.
Ключові слова: квадратна матриця, визначник( детермінанат ), алгебраїчне доповнення, мінор, система лінійних рівнянь n порядку.
ЗМІСТ
ВСТУП………………………………………………………………………………..4
РОЗДІЛ 1
ВИЗНАЧНИКИ……………………………………………………………………….6
- Квадратна матриця. Означення та історія поняття «визначник матриці»…...6
- Обчислення визначника другого та третього порядків .Метод Сюррата (трикутника)………………………………………………………………………7
1.3 Властивості визначника другого та третього порядку…………………………8
1.4 Визначники вищих порядків. Алгебраїчне доповнення……………………….10
1.5 Висновки до 1 розділу……………………………………………………………12
РОЗДІЛ 2
СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ…………………………………………………13
2.1 Основні означення систем лінійних рівнянь…………………………………...13
2.2 Габрієль Крамер та його роль у галузі лінійної алгебри……………………...14
2.3 Алагоритм та розв’язування систем рівнянь методом Крамера……………….15
2.4 Висновки до 2 розділу…………………………………………………………….21
ВИСНОВКИ…………………………………………………………………………...22
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ……………………………………………..24
ДОДАТКИ……………………………………………………………………………..26
ВСТУП
Актуальність теми роботи В сучасній шкільній освіті помітна чітка тенденція до ускладнення завдань з математики на олімпіадах, конкурсах, змаганнях тощо. Вперше я стикнувся з такою системою рівнянь при підготовці до олімпіади з математики ,що стимулювало мене до пошуку нових, оригінальних та нестандартних методів розв’язання математичних завдань.
В курсі математики середньої школи переважно вивчаються методи розв’язування систем двох лінійних рівнянь з двома невідомими. Та тільки в школах з поглибленим вивченням математики передбачається часткове вивчення систем лінійних рівнянь з більшою кількістю змінних, або ж у позакласній чи гуртковій роботі, на факультативах, при самоосвіті. Тому, щоб учні могли розв’язувати такі системи, чи задачі пов’язані з ними, та давали ґрунтовну відповідь на них, необхідно володіти загальними методами їх розв’язування.
Тому в даній роботі було зроблено ще один крок до того, щоб ознайомитись з одним з розділів сучасної математики, який є цікавим та вартим уваги для вивчення. В ній звернено увагу, в першу чергу, на сутність поняття визначника та системи лінійних рівнянь з багатьма змінними; зроблено акцент саме на метод Крамера та приклади його застосування, який необхідний для успішного та самостійного оволодіння учнями цієї теми.
Метою дослідження є надати учням та їх наставникам практичну допомогу при самостійному опрацюванні даної теми, запропонувати приклади розв’язування систем рівнянь як стандартного, так і дослідницького характеру, починаючи з найпростіших.
Для виконання сформульованої мети дослідження , були поставлені наступні завдання:
- Провести аналіз та історію виникнення та ввести понятя «матриця» , «визначник» та їх властивості ;
- Ввести поняття систем лінійних рівнянь з n невідомими та її властивостей ;
- Опрацювати правило Сюррата та формули Крамера , а також поняття «алгебраїчного доповнення».
- Побудувати і обгрунтувати алагоритм системи лінійних рівнянь n порядку ,за методом Крамера.
- Застосувати алагоритм при розв’язуванні системи лінійних рівнянь n порядку;
- Підготувати збірку систем лінійних рівнянь для самостійного опрацювання.
Предметом дослідження є системи лінійних рівнянь n порядку , які розв’язуються методом Крамера.
Методи дослідження у роботі використані такі: пошуковий по наявній літературі та інтернет ресурсах із аналізом знайденого матеріалу, порівняння, систематизація та конкретизація.
Джерельна база дослідження .Робота грунтується на аналізі методичних посібників, наукових статей, періодичних видань та напрацювань сучасних і попередніх вчених .
Структура роботи. Робота складається з 27 листків друкованого тексту і налічує 19 джерел використаної літератури.
- Квадратна матриця. Означення та історія поняття «визначник матриці»
Означення 1. Матрицею називають таблицю упорядкованих чисел або будь-яких інших об'єктів, розташованих в m рядках та п стовпцях.
Матриці позначають великими літерами, наприклад А, В, С... та круглими дужками.
Матриця, яка має однакову кількість та стовпців (m=n) , називається квадратною матрицею розміру m .
Китайський текст «Математика в дев'яти книгах» (написаний ще до нашої ери) містить приклади використання визначника для розв'язання системи рівнянь, ще задовго до введення визначників японським математиком Такакадзу Секі (1683) та німецьким математиком Лейбніцем (1693). Одне із найповніших джерел з історії визначників (до початку 20 століття) — це чотирьохтомна хрестоматія The theory of determinants in the historical order of development by Thomas Muir, New York, Dover Publications, 1960.
Означення 2. Визначником n-го порядку квадратної числової матриці А порядку п називають число, яке знаходиться з елементів матриці А за певним правилом і позначають |А|, або ∆, або det A.
1.2 Обчислення визначника другого та третього порядків .Метод Сюррата (трикутника)
Означення 3
Вираз 
(1.2. 1)
називається визначником (детермінантом) другого порядку.
Означення 4
Вираз
(1.2. 2)
називається визначником (детермінантом) третього порядку.
Символи 
називаються елементами визначника, причому перший індекс і показує номер рядка, а другий індекс j – номер стовпця, на перетині яких стоїть даний елемент. Так, елемент 
стоїть у другому рядку і третьому стовпці.
Елементи 
, 
у визначнику (1.2. 1) і , , 
у визначнику (1.2. 2) складають головну діагональ визначника, а елементи 
, 
і 
, , 
в тих самих визначниках – побічну діагональ.
Для обчислення визначника другого порядку потрібно від добутку елементів, що стоять на головній діагоналі, відняти добуток елементів, розміщених на побічній діагоналі.
Визначник третього порядку обчислюється за правилом трикутників (ПРАВИЛОМ САРРЮСА:
перші три доданки в правій частині формули (1.2 2 ) є добутками елементів, що стоять на головній діагоналі і в вершинах двох трикутників, у яких одна сторона паралельна головній діагоналі. Аналогічно утворюються доданки зі знаком мінус, де за основу береться побічна діагональ.
Приклад :
1.3 Властивості визначника другого та третього порядків .
Основні властивості визначників показано на матриці порядку.
1) Транспонування не змінює значення визначника.
Наприклад,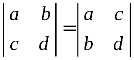 
. 
Доведення.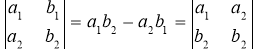 
(Ця властивість вказує на рівноправність рядків та стовпців з визначника.)
2) Якщо всі елементи рядка (або стовпця) визначника дорівнюють нулю, тоді визначник дорівнює нулю.
Наприклад, 
. 
Доведення : 
.
3) Якщо визначник має два однакові рядки (або стовпці), тоді він дорівнює нулю 
4) Якщо визначник має два пропорційні рядки (або стовпці), тоді він дорівнює нулю.
Наприклад, 
Доведення : . 
5) Якщо у визначнику поміняти місцями два рядки (або стовпці), то знак визначника зміниться на протилежний.
Наприклад, 
. 
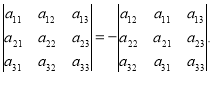
Доведення : 
6) Спільний множник рядка (або стовпця) можна винести за знак визначника.
7) Якщо до рядка (або стовпця) визначника додати його інший рядок (або стовпець), помножений на довільне число, то значення визначника не зміниться.
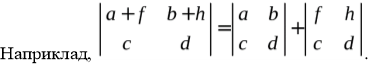
Доведення 
.
8) Якщо всі елементи рядка (або стовпця) визначника можна подати у вигляді суми двох доданків, то цей визначник дорівнює сумі визначників, які визначаються цими доданками.
1.4. Визначники вищих порядків. Алгебраїчне доповнення.
Мінором M[j,k] визначника є визначник, одержаний з даного викреслюванням рядка та стовпця, які стоять на перетині до елемента a[j,k].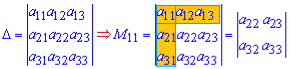
Мінори є визначниками на одиницю меншого порядку ніж матриця для якої їх шукають.
Визначник n порядку має кількість n* n мінорів (рівно кількості елементів матриці).
Для матриці 2*2 мінорами будуть протилежні елементи по діагоналі
Алгебраїчне доповнення А[j,k] – це мінор M[j,k], взятий зі знаком "плюс" , якщо j+k – парне число і зі знаком "мінус" – якщо непарне
Матриця алгебраїчних доповнень - це матриця складена з визначників А[j,k],j,k=1..n.
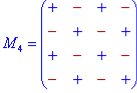
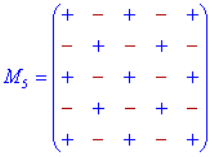
Знаки мінорів спрощено можна подати у вигляді схем
Алгебраїчне доповнення А[j,k], як і мінор, це визначник на одиницю меншого порядку ніж головний визначник. Тому для обчислення визначника n порядку потрібно обчислити n визначників n-1 порядку.
На практиці визначники матриць через алгебраїчні доповнення розписують до тих пір, поки не отримають мінори 3 порядку, які знаходять за правилом Саррюса або трикутників.
Приклад: 
1.5 Висновки
В першому розділі було дане визначення такому поняттю як квадратна матриця ,визначник, зокрема, визначник другого, третього та п-го порядків. Також у ньому наведено основні властивості визначників, способи їх обчислення, а також розкрито поняття «алгебраїчне доповнення» ,що зводить матрицю п-го порядку до 3 порядку. Показано на прикладах,як застосовувати при обчисленні визначника правило Сюррата. До кожного підрозділу наведено приклади обчислення визначників.
РОЗДІЛ 2
СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
2.1. Основні означення та види лінійних рівнянь
Системою т лінійних рівнянь з п невідомими 
називається система виду
(2.1)
Числа 
, і = 1, 2, …, т; j = 1, 2, …, п біля невідомих називаються коефіцієнтами, а числа 
– вільними членами системи (2.1).
Система рівнянь (2.1) називається однорідною, якщо всі вільні члени дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля.
Множина чисел 
називається впорядкованою, якщо вказано порядок слідування цих чисел, тобто вказано, яке з них є першим, яке другим і т. д.
Упорядкований набір п чисел 
називається розв’язком системи (2.1), якщо при підстановці цих чисел замість невідомих усі рівняння системи перетворюються в тотожності. Таку систему чисел називають також п-вимірним вектором, або точкою п-вимірного простору.
Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.
Сумісна система називається визначеною, якщо вона має єдиний розв’язок, тобто існує тільки один набір п чисел 
, який перетворює всі рівняння системи (2.1) в тотожності.
Сумісна система називається невизначеною, якщо вона має більше, ніж один розв’язок.
Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну й ту ж множину розв’язків.
2.2 Габрієль Крамер та його роль у галузі лінійної алгебри.
Габріель Крамер народився 31 липня 1704 в Женеві (Швейцарія), в сім'ї лікаря. Вже в дитинстві він випереджав своїх однолітків в інтелектуальному розвитку і демонстрував завидні здібності в області математики.
У 18 років він успішно захистив дисертацію. Через 2 роки Крамер виставив свою кандидатуру на посаду викладача в Женевському університеті. Юнак так сподобався магістрату, що спеціально для нього і ще одного кандидата на місце викладача була заснована окрема кафедра математики, де Крамер і працював в наступні роки.
Вчений багато подорожував по Європі, переймаючи досвід у знаменитих математиків свого часу — Йоганна Бернуллі і Ейлера в Базелі, Галлея і де Муавра в Лондоні, Мопертюї і Клеро в Парижі та інших. З багатьма з них він продовжував листуватися все життя.
У 1729 році Крамер відновлює викладацьку роботу в Женевському університеті. У цей час він бере участь у конкурсі Паризької Академії і займає друге місце.
Талановитий вчений написав безліч статей на самі різні теми: геометрія, історія, математика, філософія. У 1740-і роки Йоганн Бернуллі доручає Крамеру підготувати до друку збірку своїх робіт. У 1742 році Крамер публікує збірник в 4-х томах. У 1744 році він випускає посмертна збірка робіт Якоба Бернуллі (брата Йоганна Бернуллі), а також двотомник листування Лейбніца з Іоганном Бернуллі. Ці роботи викликали великий інтерес з боку вчених усього світу.
Крамер є одним з творців лінійної алгебри. Однією з найвідоміших його робіт є «Введення в аналіз алгебраїчних кривих», опублікований французькою мовою в 1750 році. У ній Крамер будує систему лінійних рівнянь і вирішує її за допомогою алгоритму, названого пізніше його ім'ям — метод Крамера.
2.3 Алагоритм розв’язування систем рівнянь методом Крамера
Нехай дано систему лінійних алгебраїчних рівнянь виду:
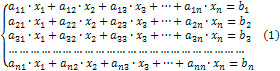
де коефіцієнти 
і 
є заданими, а вектор 
– називається розв’язком цієї системи.
Як уже зазначалося вище, якщо визначник системи (1) не дорівнює нулю (
) , то ця система має єдиний розв’язок, який знаходиться за формулами:
де 
– допоміжні визначники, які одержуються з основного визначника 
шляхом заміни його 
-го стовпця, стовпцем вільних членів системи.
Отже:
-
якщо
, то система лінійних алгебраїчних рівнянь має єдиний розв’язок, який знаходиться за формулами (2);
-
якщо
, то система (1) має безліч розв’язків (
), або вона є несумісною, тобто розв’язків не має (
).
Алгоритм розв’язку системи трьох лінійних рівнянь з трьома невідомими за методом Крамера:
- Для даної системи складаємо та обчислюємо визначник:
- Аналогічним чином обчислюємо допоміжні визначники:
3 . Використовуючи формули Крамера (2), знаходимо рішення системи (3):
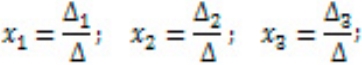
Приклад 1. Розв’язати систему: 6 х – 5у = 21,
4 х - 3 у = -5
=
= -18+20 = 2
Отже, дана система рівнянь має єдиний розв’язок:
=
= -63+(-25) = -88, 
=
= -30-88= -114.
Відповідь. (-44; -57).
Приклад 2 2 х – 7у = 2,
8 х - 3 у = 58
=
= -6+56 = 50
Отже, дана система рівнянь має єдиний розв’язок:
=
= -6+406= 400, =
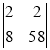= 116-16= 100
Відповідь. (8; 2).
Приклад 3 3 х + 5у = 2
3 х - 2 у =0
=
= -21
Отже, дана система рівнянь має єдиний розв’язок:
=
= -4, =
= -6
Відповідь. (
)
Приклад 4. Розв’язати систему: 
Отже, 
Відповідь. (1; 3; 2).
Приклад 5 
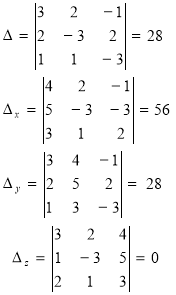
Отже, 
Відповідь. (2; -1; 0).
Приклад 6 
+3 
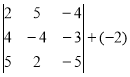
= 3×70-4×(-35)-2×35-5×(-105)=805
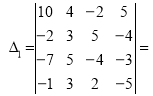10 
= 10×70-4×(-140)-2×0-5×(-70)=1610
= 3×(-140) - 10×(-35)-2×(-70)-5×175=805
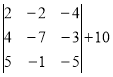
= 3×0 - 4×(-70)+10×35-5×(-35)=805
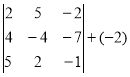
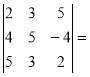
= 3×(-70) - 4×(-175)-2×(-35)-10×(-105)=1610
Отже, 
Відповідь. (2; -1; 1; 2).
Приклад 8. Розв’язати систему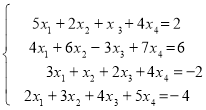 
. 
Отже, 
Приклад 8 
1 
= 1×76-2×12+3×(-2)-4×(-12) = -2
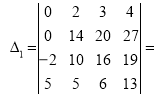0 
= 0×76-2×(-64)+3×74-4×88=0+128+222-352= -2
= 1×(-64) - 0×12+3×(-10)-4×(-24)=-64-0-30+96=2
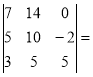
= 1× (-74) - 2×(-10)+0×(-2)-4×(-14)=-74+20+0+56=2
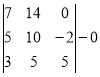
= 1×88 - 2×24+3×(-14)-0×12=88-48-42=-2
Отже,
Відповідь : ( 1; -1; -1; 1)
2.4. Висновки до 2 розділу
В другому розділі визначено поняття системи т лінійних рівнянь з п невідомими, наведено її види та властивості. Також ознайомлюємося з роллю Габрієля Крамера у розвитку лінійної алгебри та виводяться безпосередньо формули Крамера для розв’язування таких систем. Окремий підрозділ присвячений розв’язанню систем лінійних рівнянь другого, третього, четвертого порядків.
ВИСНОВКИ
В сучасній шкільній освіті помітна чітка тенденція до ускладнення завдань з математики на олімпіадах, конкурсах, змаганнях тощо. Вперше я стикнувся з такою системою рівнянь при підготовці до олімпіади з математики ,що стимулювало мене до пошуку нових, оригінальних та нестандартних методів розв’язання математичних завдань. Слід зазначити, що знання, які я здобув під час розв’язання таких завдань, розвинули нешаблонне мислення, яке я в майбутньому успішно використовуватиму і в інших сферах.
В курсі математики середньої школи переважно вивчаються методи розв’язування систем двох лінійних рівнянь з двома невідомими. Та тільки в школах з поглибленим вивченням математики передбачається часткове вивчення систем лінійних рівнянь з більшою кількістю змінних, або ж у позакласній чи гуртковій роботі, на факультативах, при самоосвіті. Тому, щоб учні могли розв’язувати такі системи, чи задачі пов’язані з ними, та давали ґрунтовну відповідь на них, необхідно володіти загальними методами їх розв’язування.
Тому в даній роботі було зроблено ще один крок до того, щоб ознайомитись з одним з розділів сучасної математики, який є цікавим та вартим уваги для вивчення. В ній звернено увагу, в першу чергу, на сутність поняття визначника та системи лінійних рівнянь з багатьма змінними; зроблено акцент саме на той метод та приклади його застосування, який необхідний для успішного та самостійного оволодіння учнями цієї теми. Це дасть їм змогу не оминати завдання цього типу і збільшити область успішно розв’язаних задач з математики.
Метою роботи було – не узагальнити все, що відомо про системи лінійних рівнянь з багатьма змінними та їх розв’язування, а надати учням та їх наставникам практичну допомогу при самостійному опрацюванні даної теми, запропонувати приклади розв’язування систем рівнянь як стандартного, так і дослідницького характеру, починаючи з найпростіших. При самостійному опрацюванні добре розвивається інтуїція, логічне мислення, розумові здібності, вміння узагальнювати та конкретизувати.
Варто підкреслити, що процес розв'язування систем лінійних рівнянь, який був показаний вище, – це непроста, цікава пошукова робота, адже дана тема є набагато ширшою і багатогранною. Перед розв'язком даних систем лінійних рівнянь потрібно перевірити необхідні умови застосування методу Крамера:
1. Кількість рівнянь системи дорівнює кількості невідомих.
2. Визначник основної матриці системи не дорівнює нулю.
Також даний метод можна застосовувати і для великих значень n, але він потребує більше розрахунків. У випадку, коли n > 3 доцільно використовувати метод Гауса з поступовим виключенням змінних, одиничною діагоналлю. У майбутньому я досліджуватиму ці способи розв'язування.
Тому в класах із поглибленим вивченням математики, фізико-математичного профілю, при роботі зі здібними та обдарованими учнями у звичайних класах, ставлячи завдання розвитку продуктивного мислення при вивченні курсу алгебри і початків аналізу, варто розглядати системи лінійних рівнянь з трьома і більше змінними та відомі способи їх розв'язування.
У додатках підібрана збірка систем лінійних рівнянь n -го для самостійного опрацювання.
Сподіваюсь, що дана робота допоможе учням, які цікавляться математикою, опанувати цю тему і стати більш обізнанішими в знаннях з математики ,а вчителі зможуть використати її при проведенні уроків, гуртків чи факультативів.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Дубовик В. П., Юрик І. І. Вища математика. Навчальний посібник. – К.: А.С.К., 2006. – 648 с.
- Клепко В. Ю., Голець В. Л. Вища математика в прикладах і задачах. Навчальний посібник. 2-ге видання. – К.: Центр учбової літератури, 2009. – 594 с.
- Назієв Е. Х., Владіміров В. М., Миронець О. А. Лінійна алгебра та аналітична геометрія. Навчальний посібник. – К.: Либідь, 1997. – 152 с.
- Стаття із журналу: Михалькова І. М. Теорія матриць // Математика в школах України. Позакласна робота (Харків, ВГ «Основа»). – 2011.– № 8(8). – С. 23-28.
- Студентські фізико-математичні етюди. – Київ: Вид-во НПУ імені М. П. Драгоманова. – 2012. – № 11, том 2. – 123 с.
- Чарін В.С. Лінійна алгебра. 2-е вид., стер. – К.: Техніка, 2005. – 416 с.
- Каплан І.А Практичні заняття з вищої математики. Частина 1,Харків – 1973.- 204 с.
- Пастушенко С. М.; Підченко Ю. П. (2002 р.). Вища математика. Основні поняття, формули, зразки розв'язування задач. Київ: Діал. ISBN 966-591-025-6.
- https://studfile.net/preview/9441262/page:3/
- https://studfile.net/preview/7349415/page:3/
- Метод Крамера // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 30. — 594 с.
- Розв'язати Систему Лінійних Рівнянь (3х3) Методом Крамера (mathros.net.ua)
- ↑ Cramer, Gabriel (1750). Introduction à l'Analyse des lignes Courbes algébriques (фр.). Geneva: Europeana. с. 656–659. Архів оригіналу за 15 вересня 2019. Процитовано 18 травня 2012.
- ↑ Kosinski, A. A. (2001). Cramer's Rule is due to Cramer. Mathematics Magazine 74: 310–312. doi:10.2307/2691101.
- ↑ MacLaurin, Colin (1748). A Treatise of Algebra, in Three Parts..
- ↑ Boyer, Carl B. (1968). A History of Mathematics (вид. 2nd). Wiley. с. 431.
- ↑ Katz, Victor (2004). A History of Mathematics (вид. Brief). Pearson Education. с. 378–379.
- ↑ Hedman, Bruce A. (1999). An Earlier Date for "Cramer's Rule". Historia Mathematica 26 (4): 365–368. doi:10.1006/hmat.1999.2247. Архів оригіналу за 21 липня 2018. Процитовано 6 травня 2021.
ДОДАТКИ
1 
2 
3 
4 
5 
6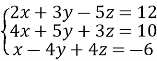 
7 
8 
9 
10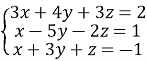 
11 
12 
13 
14 
15 
16 
17 
18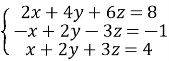 
19 
20 
21 
22 
23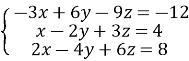 
24 
25 
26 
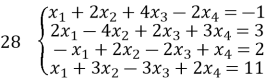
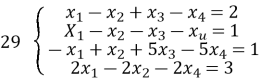
про публікацію авторської розробки
Додати розробку