Науково-дослідницька робота МАН "Розв’язування систем лінійних рівнянь методом Крамера"
Про матеріал
Дана презентація до науково-дослідницької роботи МАН "Розв’язування систем лінійних рівнянь методом Крамера" Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





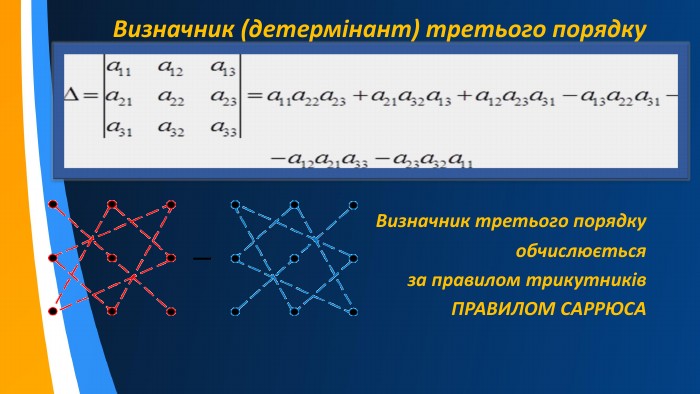

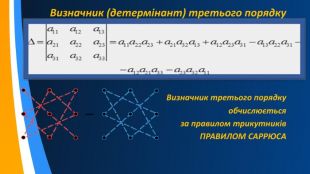
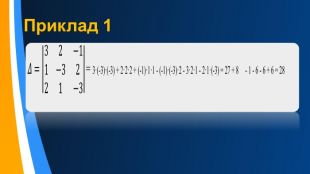
![Мінором M[j,k] визначника є визначник, одержаний з даного викреслюванням рядка та стовпця, які стоять на перетині до елемента a[j,k]. Мінори є визначниками на одиницю меншого порядку ніж матриця для якої їх шукають. Мінором M[j,k] визначника є визначник, одержаний з даного викреслюванням рядка та стовпця, які стоять на перетині до елемента a[j,k]. Мінори є визначниками на одиницю меншого порядку ніж матриця для якої їх шукають.](/uploads/files/2381578/337091/389852_images/7.jpg)
![Алгебраїчне доповнення А[j,k] – це мінор M[j,k], взятий зі знаком Алгебраїчне доповнення А[j,k] – це мінор M[j,k], взятий зі знаком](/uploads/files/2381578/337091/389852_images/8.jpg)