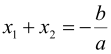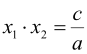Науково – дослідницька робота «Нестандартні способи розв’язування квадратних рівнянь»
ЗМІСТ
ВСТУП 4
-
Розділ І. Історія розвитку квадратних рівнянь 6
- Квадратні рівняння в Стародавньому Вавилоні 6
- Діофантові квадратні рівняння 6
- Квадратні рівняння в Індії 7
- Квадратні рівняння в Європі 8
-
Розділ ІІ. Способи розв’язування квадратних рівнянь. 9
- Розв’язування квадратних рівнянь за формулами. 9
- Розв’язування квадратних рівнянь за теоремою Вієта 11
- Метод виділення повного квадрату. 15
- Розкладання лівої частини рівняння на множники. 16
- Властивості коефіцієнтів квадратного рівняння. 17
- Розв’язування квадратного рівняння способом «перекидання». 19
- Розв’язування квадратних рівнянь графічним способом. 21
- Квадратні рівняння з модулями 22
- Висновок 23
- Список використаних джерел 24
ВСТУП
На протязі багатьох років алгебру розглядали як науку про рівняння і способи їх розв’язування. Велике значення рівнянь підкреслював А.Ейнштейн. Він сказав: „Мені доводилось ділити свій час між політикою і рівнянням. Проте рівняння, на мій погляд, набагато важливіші, тому що політика існує тільки для даного часу, а рівняння будуть існувати вічно”.
В сучасній математиці підчас підготовки до олімпіад з математики, до зовнішнього незалежного оцінювання ми зустрічаємося із значним обсягом рівнянь, які потрібно розв’язати за обмежений проміжок часу.
В шкільному курсі математики вивчаються формули коренів, за допомогою яких можна розв’язувати будь-яке квадратне рівняння.
Однак існують і інші прийоми розв’язування квадратних рівнянь, які дозволяють дуже швидко і раціонально їх розв’язувати.
Серед даних завдань часто зустрічаються такі, які ставлять за мету перевірити у нас, здобувачів освіти, не стільки технічні навички, скільки уважність, уміння знайти найкоротший шлях розв’язання, застосувавши при цьому нетрадиційний, оригінальний метод тощо. Тому на сьогоднішній день дуже важливо оволодіти найрізноманітнішими можливостями правильного оформлення алгоритму розв’язування рівнянь, який би не містив громіздких викладень, але за допомогою яких ми б змогли продемонструвати яскраві, ефективні, а інколи і несподівані застосування теоретичного матеріалу. Такі прийоми я намагався знайти в додатковій літературі, в Інтернеті, а потім, узагальнивши їх, застосував в інших умовах до розв’язування різноманітних рівнянь. Ці прийоми тісно пов’язані з матеріалом, що вивчається в школі, але, крім того, їх нестандартне розв’язання вчить нас, не задовольнятися шаблонами, алгоритмами, а вдумливо підходити до пошуку оригінальних розв’язань. Так була написана дана науково-дослідна робота.
Актуальність теми полягає в тому, що в ній висвітлено проблему розв’язування квадратних рівнянь.
Мета роботи: розгляд, аналіз, систематизація та узагальнення методів розв’язування квадратних рівнянь.
Реалізація цієї мети передбачає виконання таких основних завдань:
- здійснити огляд та аналіз літератури з даної тематики;
- виявити і систематизувати різні способи розв’язування квадратних рівнянь і знайти найефективніші з них;
- розширити свої знання з математики.
Практичне значення науково-дослідницької роботи полягає в тому, що її результати можуть бути використані як практичний посібник для здобувачів освіти та вчителів на різних етапах вивчення математики: як додатковий і цікавий матеріал на уроках з математики, математичних гуртках та факультативах, а також здобувачі освіти можуть використовувати її у підготовці до ДПА і зовнішнього незалежного оцінювання.
Розділ І. Історія розвитку квадратних рівнянь
- .Квадратні рівняння в Стародавньому Вавилоні
У Стародавньому Вавилоні необхідність розв'язувати рівняння не тільки першого, але і другого степеня була викликана потребою вирішувати задачі, пов'язані із знаходженням площ земельних ділянок та земляними роботами військового характеру, а також з розвитком астрономії і самої математики.
Приклад, взятий з однієї глиняної таблички цього періоду.
«Площа, яка складається з суми двох квадратів, становить 1000. Сторона одного з квадратів становить сторони іншого квадрата, що зменшені на 10. Які сторони квадратів?»
Це призводить до рівнянь, розв'язання яких зводиться до розв'язування квадратного рівняння , що має додатний корінь .
Насправді розв’язування у клинописному тексті обмежується простим перерахуванням етапів обчислення, необхідного для розв'язування квадратного рівняння:
«Піднеси до квадрату 10; це дає 100; відніми 100 від 1000; це дає 900» і т. Д
 1.2. Діофантові квадратні рівняння
1.2. Діофантові квадратні рівняння
Діофант Олександрійський - давньогрецький математик , який жив приблизно в III ст. н. е.
Завдання: «Знайти два числа, знаючи, що їх сума дорівнює 20, а добуток - 96»
Діофант міркує таким чином: з умови задачі випливає, що шукані числа не рівні, так як якщо б вони були рівні, то їх добуток дорівнювало б не 96, а 100. Таким чином, одне з них буде більше половини їх суми, тобто 10 + х, інша ж менше, тобто 10 - х. Різниця між ними 2х.
Маємо рівняння:
(10 + х)(10 - х) = 96
або ж:
100 - х²= 96
х²- 4 = 0 (1)
Звідси х = 2. Одне з шуканих чисел дорівнює 12, інше 8.
Розв’язок х = -2 для
Діофанта не існує, так як грецька математика знала тільки додатні числа.
Якщо ми розвяжемо цю задачу, вибираючи в якості невідомого одне з шуканих чисел, то ми прийдемо до розв’язування рівняння
у(20 - у) = 96,
у² - 20у + 96 = 0. (2)
Зрозуміло, що, вибираючи в якості невідомого піврізницю шуканих чисел, Діофант спрощує розв’язування; йому вдається звести задачу до розв’язування неповного квадратного рівняння (1).
- Квадратні рівняння в Індії
Одна із задач відомого індійського математика XII ст. Бхаскари:
«Мавпочок жвавих зграя,
Всмак поївши, розважалася.
Їх в квадраті частина восьма,
На галявині бавилася.
А дванадцять по ліанах ...
Стали стрибати, повисаючи ...
Скільки ж було мавпочок,
Ти скажи мені, в цій зграї? »
Розв’язування Бхаскари свідчать про те, що він знав про кількість коренів квадратних рівнянь.
Відповідне рівняння задачі
( 1/8 х)²+12=х
Бхаскара пише під виглядом х²- 64х = -768 і, щоб доповнити ліву частину цього рівняння до квадрата, додають до обох частин 32², отримуючи потім:
х² -64х+32²=-768+1024,
(х-32)²=256,
х-32=±16,
![]() = 16,
= 16, ![]() = 48
= 48
-

 Квадратні рівняння в Європі
Квадратні рівняння в Європі
В Європі XIII – XVII століття, математикою займалися французький математик Франсуа Вієт та італійський математик Леонардо Фібоначчі.
В даний час вміння розв'язувати квадратні рівняння необхідно для всіх. Вміння швидко, раціонально і правильно розв’язувати квадратні рівняння полегшує вивчення багатьох тем курсу математики.. Більшість практичних задач реального світу теж зводиться до розв'язання квадратних рівнянь.
Розділ ІІ. Способи розв’язування квадратних рівнянь.
- Розв’язування квадратних рівнянь за формулами.
В шкільному курсі математики застосовується розв’язування рівнянь за формулою. Виведемо формулу коренів квадратного рівняння ![]() .
.
Помноживши обидві частини рівняння ![]() на
на ![]() , дістанемо:
, дістанемо:
![]() ,
,
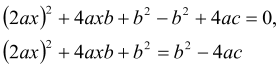
і далі, використавши формулу квадрата суми отримаємо:
![]() .
.
Вираз ![]() називається дискримінантом і позначається
називається дискримінантом і позначається ![]() .
. ![]() .
.
Дискримінант походить від латинського diskriminans – той, що розрізняє або розрізняючий. Дискримінант відіграє важливу роль. За його значенням можна визначити (розрізнити) скільки коренів має квадратне рівняння ![]() .
.
Встановимо залежність коренів від дискримінанта:
-
Якщо
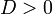 , то квадратне рівняння рівносильне рівнянню
, то квадратне рівняння рівносильне рівнянню 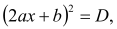
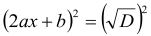 , звідки
, звідки 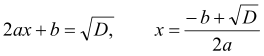
або 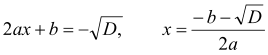
У цьому випадку дане рівняння має два корені, які відрізняються лише знаком перед ![]() . Коротко ці корені записують так: [8,150]
. Коротко ці корені записують так: [8,150]
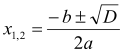 , де
, де ![]() (2.1).
(2.1).
-
Якщо
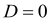 , то
, то 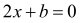 , звідки
, звідки 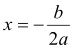 — єдиний корінь (правильніше – два однакові корені)
— єдиний корінь (правильніше – два однакові корені)
-
Якщо
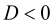 , то дане рівняння не має дійсних коренів. Але при цьому є можливість знайти два комплексних корені за формулою (1) або, скориставшись наступною формулою, щоб не добувати корінь з від’ємного числа:
, то дане рівняння не має дійсних коренів. Але при цьому є можливість знайти два комплексних корені за формулою (1) або, скориставшись наступною формулою, щоб не добувати корінь з від’ємного числа: 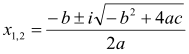 (2.2).
(2.2).
1. Розв’язати рівняння: ![]() .
.
Розв’язання: Маємо: ![]() , то
, то 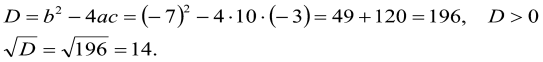 , два різних корені:
, два різних корені: 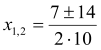 ;
;
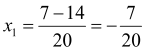 ,
, 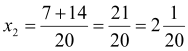
Відповідь: 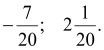
2. Розв’язати рівняння: ![]()
![]()
Розв’язання: Маємо: ![]() , то
, то 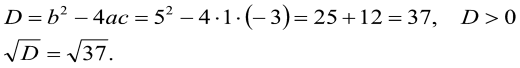
Отже, рівняння має два різних корені: 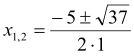 ;
;
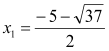 ,
, 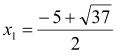
Відповідь: 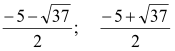 .
.
- Розв’язування квадратних рівнянь за теоремою Вієта
Свою відому на весь світ теорему Вієт відкрив у 1591 році. Для квадратного рівняння в сучасних позначеннях вона мала такий вигляд: коренями рівняння ![]()
Розглянемо будь-яке зведене квадратне рівняння ![]() , яке має корені.
, яке має корені.
Теорема (для зведеного квадратного рівняння). Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому із протилежним знаком, а добуток коренів дорівнює вільному члену.
|
|
Доведення. Розглянемо зведене квадратне рівняння ![]() . Дискримінант цього рівняння
. Дискримінант цього рівняння ![]() . Якщо
. Якщо ![]() , то рівняння має два корені:
, то рівняння має два корені:
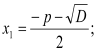
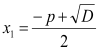 .
.
Знайдемо суму і добуток коренів:
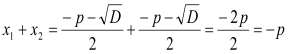 ;
;
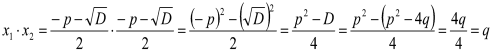 .
.
Отже, ![]() ,
, ![]() . Теорему доведено.
. Теорему доведено.
Зауваження. Якщо в рівнянні ![]() число q є цілим, то з рівності
число q є цілим, то з рівності ![]() випливає, що цілими коренями такого рівняння можуть бути лише дільники числа q (вільного члена).
випливає, що цілими коренями такого рівняння можуть бути лише дільники числа q (вільного члена).
Ця теорема справедлива і для повного квадратного рівняння. Сформулюємо та доведемо її.
Теорема (для повного квадратного рівняння). Сума коренів повного квадратного рівняння дорівнює відношенню другого коефіцієнта до першого, взятого з протилежним знаком, а добуток коренів дорівнює відношенню вільного члена до першого коефіцієнта.
|
|
Доведення. Знайдемо суму і добуток його коренів.
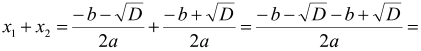
![]()
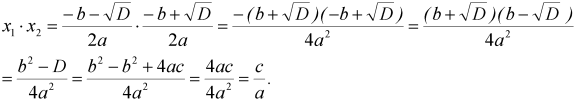
Отже, ![]() ,
, 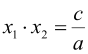 .
.
Теорему доведено.
Отже, на основі теореми Вієта можна:
- не обчислюючи коренів квадратного рівняння, знаходити їхню суму та добуток;
- Використовувати теорему Вієта можна лише для квадратних рівнянь, які мають корені.
Обернена теорема Вієта
Справджується також твердження, обернене до теореми Вієта.
Теорема (для зведеного квадратного рівняння). Якщо числа m і n такі, що їх сума дорівнює ![]() , а добуток дорівнює
, а добуток дорівнює ![]() , то ці числа є коренями рівняння
, то ці числа є коренями рівняння ![]() .
.
|
якщо
|
Наслідки з теореми, оберненої до теореми Вієта
-
Числа
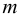 і
і 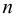 корені – корені рівняння
корені – корені рівняння 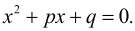
-
Якщо
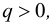 то корені рівняння
то корені рівняння 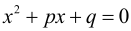
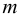 і
і 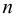 мають однаковий знак (обидва додатні або обидва від’ємні). Причому, якщо
мають однаковий знак (обидва додатні або обидва від’ємні). Причому, якщо 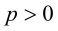 , то обидва корені від’ємні, а якщо
, то обидва корені від’ємні, а якщо 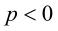 , то обидва корені додатні.
, то обидва корені додатні.
-
Якщо
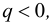 то корені рівняння
то корені рівняння 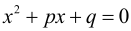
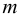 і
і 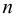 мають різні знаки, причому більший за модулем корінь буде додатній, якщо
мають різні знаки, причому більший за модулем корінь буде додатній, якщо 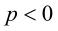 і від’ємні, якщо
і від’ємні, якщо 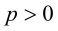 .
.
Теорема (для повного квадратного рівняння). Якщо числа m і n такі, що їх сума дорівнює ![]() , а добуток дорівнює
, а добуток дорівнює ![]() , то ці числа є коренями рівняння
, то ці числа є коренями рівняння ![]() .
.
Доведення. Поділимо обидві частини рівняння ![]() на
на ![]() :
:
![]()
За умовою, ![]() і
і 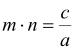 . Підставимо в рівняння замість
. Підставимо в рівняння замість ![]() і
і ![]() їх значення. Дістанемо:
їх значення. Дістанемо:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Звідки ![]() , і
, і ![]() ,
,
![]()
![]()
Теорему, обернену до теореми Вієта, зручно застосовувати у процесі розв’язування зведених квадратних рівнянь.
Отже, на основі теореми, оберненої до теореми Вієта, можна
- перевірити, чи є деякі два числа коренями заданого квадратного рівняння;
- розв’язати квадратне рівняння шляхом підбору його коренів;
- записати зведене квадратне рівняння, коренями якого є деякі задані числа.
Задача 1. Рівняння ![]() має корені. Не розв’язуючи рівняння, знайти суму та добуток його коренів.
має корені. Не розв’язуючи рівняння, знайти суму та добуток його коренів.
Розв’язання. Нехай ![]() і
і ![]() корені рівняння. За теоремою Вієта
корені рівняння. За теоремою Вієта
Відповідь. 12; 20.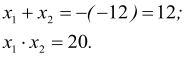
Задача 2. Розв’язати рівняння ![]() , використовуючи теорему Вієта.
, використовуючи теорему Вієта.
Розв’язання. Нехай ![]() і
і ![]() – корені рівняння. Тоді
– корені рівняння. Тоді
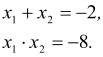
Якщо ![]() та
та ![]() – цілі числа, то рівність
– цілі числа, то рівність ![]() правильна лише для пар чисел: –1 і 8; –2 і 4; –4 і 2; –8 і 1. Із цих пар лише сума чисел третьої пари дорівнює –2. Тому за теоремою, оберненою до теореми Вієта, числа –4 і 2 будуть коренями заданого квадратного рівняння. Отже,
правильна лише для пар чисел: –1 і 8; –2 і 4; –4 і 2; –8 і 1. Із цих пар лише сума чисел третьої пари дорівнює –2. Тому за теоремою, оберненою до теореми Вієта, числа –4 і 2 будуть коренями заданого квадратного рівняння. Отже, ![]() ,
, ![]() .
.
Відповідь. –4; 2.
- Метод виділення повного квадрату
1. Розв’язати рівняння: ![]()
Розвязання: Виділимо квадрат двочлена в лівій частині:
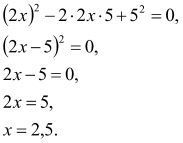
Відповідь: ![]()
2. Розв’язати рівняння: ![]() .
.
Розв’язання: Виділимо квадрат двочлена в лівій частині: ![]() .
.
Отже, дане квадратне рівняння можна записати так:
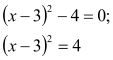

Отже, ![]() – є коренями рівняння.
– є коренями рівняння.
Відповідь: ![]()
- Розв’язати рівняння, виділивши квадрат двочлена:
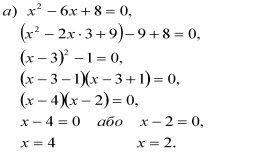
Відповідь. 2, 4.
- Розкладання лівої частини рівняння на множники
1. Розв’язати рівняння: ![]() .
.
Розв’язання: Розкладемо ліву частину рівняння на множники, ![]() Отже, дане квадратне рівняння можна записати так:
Отже, дане квадратне рівняння можна записати так:![]() . Оскільки, добуток дорівнює 0, коли хоча б один із множників дорівнює 0, тому отримаємо:
. Оскільки, добуток дорівнює 0, коли хоча б один із множників дорівнює 0, тому отримаємо:

Отже, ![]() – є коренями рівняння.
– є коренями рівняння.
Відповідь: ![]() .
.
-
Розв’язати рівняння:
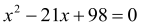 .
.
Розв’язання: Розкладемо ліву частину рівняння на множники, ![]() . Отже, дане квадратне рівняння можна записати так:
. Отже, дане квадратне рівняння можна записати так:
![]() .
.
Оскільки, добуток дорівнює 0, коли хоча б один із множників дорівнює 0, то отримаємо:

Отже, ![]() – є коренями рівняння.
– є коренями рівняння.
Відповідь: ![]()
- Властивості коефіцієнтів квадратного рівняння
Серед квадратних рівнянь є й такі типи рівнянь, які можна розв’язувати усно використовуючи властивості їх коефіцієнтів. Розглянемо ці рівняння.
Нехай дано квадратне рівняння
![]() , де
, де ![]() .
.
Сума коефіцієнтів квадратного рівняння дорівнює нулю
Якщо ![]() (тобто, сума коефіцієнтів дорівнює нулю), то
(тобто, сума коефіцієнтів дорівнює нулю), то ![]()
Доведення. Розділимо обидві частини рівняння на а, одержимо зведене квадратне рівняння
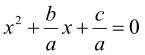
Відповідно до теореми Вієта
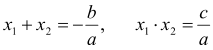
За умовою ![]() , звідки
, звідки ![]() . Отже,
. Отже,
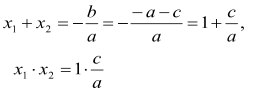
Отримаємо, ![]() і
і ![]() , що й потрібно було довести.
, що й потрібно було довести.
Приклади.
1. Розв’язати рівняння: ![]()
Розв’язання: Оскільки ![]()
![]() , то
, то ![]()
![]() ,
, 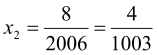
Відповідь: ![]() .
.
2. Розв’язати рівняння: ![]()
![]()
Розв’язання: Оскільки ![]()
![]() , то
, то ![]()
![]() ,
, 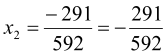 .
.
Відповідь: ![]() .
.
3. Розв’язати рівняння: ![]()
![]()
Розв’язання: Оскільки ![]()
![]() , то
, то ![]()
![]() ,
, 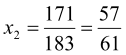
Відповідь: ![]() .
.
Другий коефіцієнт квадратного рівняння
дорівнює сумі першого і третього
Якщо ![]() (тобто, якщо другий коефіцієнт дорівнює сумі першого і третього коефіцієнтів), то
(тобто, якщо другий коефіцієнт дорівнює сумі першого і третього коефіцієнтів), то 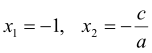
Доведення. Розділимо обидві частини рівняння на а, одержимо зведене квадратне рівняння
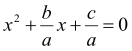
Відповідно до теореми Вієта
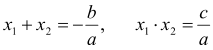
За умовою ![]() . Отже,
. Отже,
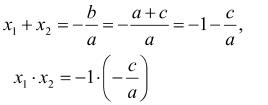
Отримаємо, ![]() і
і 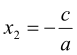 , що й потрібно було довести.
, що й потрібно було довести.
1. Розв’язати рівняння: ![]()
![]()
Розв’язання: Оскільки ![]()
 , то
, то ![]()
![]() ,
, 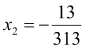
Відповідь: ![]() .
.
2. Розв’язати рівняння: ![]()
![]()
Розв’язання: Оскільки ![]()
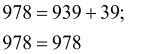 , то
, то ![]() ,
, 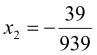
Відповідь: ![]() .
.
- Розв’язування квадратних рівнянь способом «перекидання»
Нехай дано квадратне рівняння
![]() , де
, де ![]() .
.
Домноживши обидві частини рівняння на ![]() , отримаємо рівняння
, отримаємо рівняння ![]() .
.
Введемо заміну. Нехай ![]() , то
, то 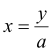 . Підставивши значення
. Підставивши значення ![]() , одержимо рівняння
, одержимо рівняння ![]() , яке рівносильне даному. Корені цього рівняння
, яке рівносильне даному. Корені цього рівняння ![]() і
і ![]() знайдемо за допомогою теореми Вієта. Остаточно отримуємо
знайдемо за допомогою теореми Вієта. Остаточно отримуємо 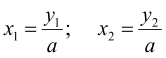 .
.
При цьому способі коефіцієнт ![]() множиться на вільний член, якби «перекидається» до нього, тому його називають способом «перекидання». Даний спосіб застосовують тоді, коли можна легко знайти корені рівняння, використовуючи теорему Вієта і, що найважливіше, коли дискримінант є точний квадрат.
множиться на вільний член, якби «перекидається» до нього, тому його називають способом «перекидання». Даний спосіб застосовують тоді, коли можна легко знайти корені рівняння, використовуючи теорему Вієта і, що найважливіше, коли дискримінант є точний квадрат.
1. Розв’язати рівняння: ![]()
![]()
«Перекинувши» коефіцієнт 5 до вільного члена, в результаті отримаємо рівняння ![]() .
.
За теоремою Вієта ![]() ,
, ![]() .
.
Отже, 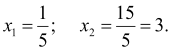
Відповідь: 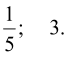
2. Розв’язати рівняння: ![]() .
.
«Перекинувши» коефіцієнт 2 до вільного члена, в результаті отримаємо рівняння ![]() .
.
За теоремою Вієта ![]() ,
, ![]() .
.
Отже, 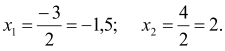
Відповідь: ![]()
- Розв’язування квадратних рівнянь графічним способом.
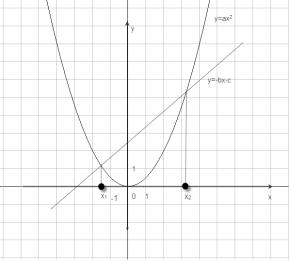
Якщо в рівнянні ![]() перенести другий і третій члени в другу частину, то одержимо
перенести другий і третій члени в другу частину, то одержимо ![]()
Побудуємо графіки ![]() та
та ![]() Графік першої функції парабола, що проходить через початок координат, а другої – пряма.
Графік першої функції парабола, що проходить через початок координат, а другої – пряма.
Можливі такі випадки:
- пряма і парабола можуть перетинатися в двох точках, абсциси точок перетину є коренями квадратного рівняння; (два корені).
- пряма і парабола можуть дотикатися в одній точці, абсциса якої є коренем квадратного рівняння; (один корінь)
- пряма і парабола не мають спільних точок, тобто квадратне рівняння не має коренів.
1. Розв’язати рівняння: ![]() .
.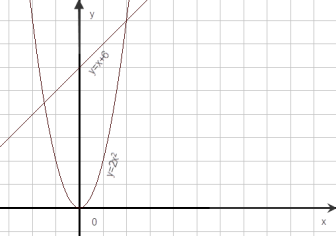
Перетворимо дане рівняння ![]() . Побудуємо графіки
. Побудуємо графіки ![]()
Пряма і парабола перетинаються в двох точках з абсцисами ![]() і
і ![]() тому рівняння має два корені.
тому рівняння має два корені.
- Розв’язування квадратних рівнянь з модулями
-
Розв’язати рівняння
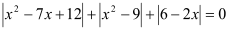 .
.
Розв’язання.
Задане рівняння рівносильне системі 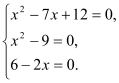
З третього рівняння одержуємо х = 3, що задовольняє і всій системі.
Отже, задане рівняння має єдиний корінь х = 3.
Відповідь. 3.
-
Розв’язати рівняння:
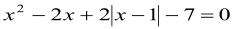 .
.
Розв’язання.
Оскільки ![]() тоді дане рівняння матиме вид
тоді дане рівняння матиме вид ![]() , то зробимо заміну
, то зробимо заміну
![]() Тоді
Тоді ![]()
Отже, ![]() – корені даного рівняння.
– корені даного рівняння.
Відповідь. – 1; 3.
ВИСНОВОК
Людство пройшло тривалий шлях від незнання до знання, безперервно міняючи на цьому шляху неповне і недосконале знання на більш повне і досконале.
Працюючи над даною дослідницькою роботою, я більш детально ознайомився з поняттям квадратного рівняння, а також з різними способами їх розв’язування. Мені вдалося узагальнити і систематизувати вивчений матеріал по вище зазначеній темі.
Працюючи над даною темою я зрозумів, що способів розв’язування квадратних рівнянь є дуже багато. Я знайшов, розглянув і зрозумів 7 способів, але на мою думку їх є набагато більше. Тому я не зупинюся на досягнутому і в майбутньому знову буду шукати красиві закономірності, факти, робити узагальнення, відкриваючи для себе все нове і нове.
Потрібно відзначити, що не всі вони зручні для розв’язування, але кожен з них є унікальним. Деякі з наведених вище способів допомагають заощадити час, що дуже важливо при виконанні самостійних, контрольних робіт, при розв’язуванні завдань на ДПА чи в майбутньому на ЗНО. Досить часто при розв’язуванні квадратних рівнянь можна використати кілька способів та прийомів, що описані вище. В даній роботі я розглянув також квадратні рівняння, що містять модуль. Дана тема несе багато прихованого і невідомого, що дає чудову можливість подальшої роботи з нею.
Результати моїх досліджень зацікавили багатьох здобувачів освіти нашої школи, а особливо дев’ятикласників та одинадцятикласників, які хочуть опанувати деякі способи розв’язування квадратних рівнянь для того, щоб економити час в майбутньому.
Підводячи підсумки, можна зробити висновок: квадратні рівняння відіграють величезну роль в математиці.
Саме робота над даною темою розширила мої теоретичні знання, сприяла поглибленню практичних вмінь та навичок, а також розширила рівень володіння основними математичними знаннями та вміннями.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Алімов.Ш.А., Ільїн В.А. та інших.Алгебра, 6-8. Пробний підручник для 6-8 класової середньої школи. - М., Просвітництво, 1981.
- Абрамчук В.С., Тютюн А.А., Шунда Н.М. Посібник з шкільного курсу математики.
- Істер О.І. Підручник. Алгебра 8 клас., Київ. Генеза – 2016 рік
- Практикум з розв’язування задач з математики. За редакцією В.І.Михайлівського. – Київ: “Вища школа”, 1989 р.
- Сарана О.А. Математичні олімпіади: просте і складне поруч. – Київ: “Видавництво А.С.К.”, 2004 р.
- Конет І.М., Паньков В.Г.,Радченко В.М., Теплінський Ю.В. Обласні математичні олімпіади. – Каменець-Подільський: Абетка, 2010
Інтернет – ресурси :
- https://uk.wikipedia.org/wiki/
- https://www.google.com.ua/url?sa=t&rct=j&q=&esrc=s&source=web&cd=6&cad=rja&uact=8&ved=2ahUKEwj58bie5fvmAhWwk4sKHSEjAHkQtwIwBXoECAoQAQ&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3DMc15I2VuQII&usg=AOvVaw0Serl98j268AO6nFeLlLX3
- https://www.google.com.ua/url?sa=t&rct=j&q=&esrc=s&source=web&cd=7&cad=rja&uact=8&ved=2ahUKEwj58bie5fvmAhWwk4sKHSEjAHkQFjAGegQIBRAB&url=https%3A%2F%2Fua-referat.com%2F%25D0%259A%25D0%25B2%25D0%25B0%25D0%25B4%25D1%2580%25D0%25B0%25D1%2582%25D0%25BD%25D1%2596_%25D1%2580%25D1%2596%25D0%25B2%25D0%25BD%25D1%258F%25D0%25BD%25D0%25BD%25D1%258F_%25D1%2582%25D0%25B0_%25D1%2580%25D1%2596%25D0%25B2%25D0%25BD%25D1%258F%25D0%25BD%25D0%25BD%25D1%258F_%25D0%25B2%25D0%25B8%25D1%2589%25D0%25B8%25D1%2585_%25D0%25BF%25D0%25BE%25D1%2580%25D1%258F%25D0%25B4%25D0%25BA%25D1%2596%25D0%25B2&usg=AOvVaw3uLv6csqIwU9slVxGbD89v
-
Браво!


про публікацію авторської розробки
Додати розробку