Урок систематизації вмінь та навичок по темі: Розв’язування тригонометричних рівнянь, систем рівнянь та нерівностей.
Мета уроку: -повторити розв'язки основних тригонометричних рівнянь;
- вміти застосовувати їх на практиці;
- вчити учнів аналізувати та систематизувати ті знання, які вони отримують на уроках і черпають з додаткової літератури;
-формувати наполегливість, увагу, зосередженість та зацікавленість у результатах спільної роботиУрок систематизації вмінь та навичок по темі:
Розв’язування тригонометричних
рівнянь, систем рівнянь та нерівностей.
Необхідний час – 90хв.
Мета уроку: - повторити розв’язки основних тригонометричних рівнянь;
- вміти застосовувати їх на практиці;
- вчити учнів аналізувати та систематизувати ті знання, які вони отримують на уроках і черпають з додаткової літератури;
-формувати наполегливість, увагу, зосередженість та зацікавленість у результатах спільної роботи.
Тип уроку: урок узагальнення і систематизації знань з використанням інтерактивних технологій ( робота в групах ).
Напис на дошці: Математика цікава тоді, коли дає поживу нашій винахідливості й здатності до міркувань.
за Д.Пойа
На уроці учні працюють групами, склад яких, заздалегідь продуманий вчителем, визначається на початку уроку. На першому уроці учні пригадують тригонометричні рівняння та основні методи їх розв’язання. На другому уроці кожній групі дається по 2 різних завдання (на розв’язання яких відводиться до 8 хв.) з подальшою демонстрацією кожного з них біля дошки. Біля дошки відповідає один представник групи, яка найшвидше справилася із завданням (на вибір капітана даної групи). Всі уважно слухають доповідача, після чого члени інших груп вносять свої пропозиції щодо розв’язання задачі, дають запитання доповідачеві. З’ясувавши шлях розв’язання задачі, учні записують його в зошити.
Структура уроку:
1. Організаційний момент.
2. Повідомлення теми та мети уроку.
3. Актуалізація опорних вмінь та навичок.
- Узагальнення та повторення раніше здобутих знань.
- Підведення підсумків уроку.
Хід уроку
- Організаційний момент.
- Повідомлення теми та мети уроку.
Вчитель нагадує, що після цього уроку слідує контрольна робота.
- Актуалізація опорних вмінь та навичок
У формі фронтальної бесіди проводиться повторення вивченого матеріалу.
Питання для учнів:
1. Сформулювати загальний розв’язок найпростіших тригонометричних рівнянь, їхні окремі випадки.
2. Як знайти розв’язок системи тригонометричних рівнянь?
3. Для розминки пропонуються тренувальні вправи (учні біля дошки):
Розв’язати рівняння (завдання записані на дошці):
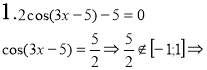 ;
;
Рівняння розв’язків не має.
 ;
;
![]() .
.
- Назвіть основні способи розв’язування тригонометричних рівнянь:
А) найпростіші тригонометричні рівняння;
Б) рівняння, які зводяться до однієї тригонометричної функції (зведення до квадратних рівнянь);
В) розкладання на множники;
Г) однорідні тригонометричні рівняння (1-го і 2-го степеня);
Д) дробово-раціональні рівняння;
Е) універсальна заміна.
На дошці записано умови рівнянь. Учні повинні назвати спосіб, за яким будуть розв’язувати кожне із рівнянь.
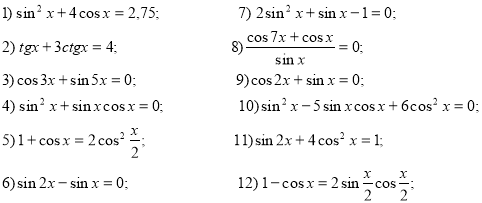
- Узагальнення та повторення раніше здобутих знань.
Оголошується склад груп. Кожна група отримує завдання та час на його виконання. Група, яка найшвидше справиться із завданням, починає його захищати біля дошки. Представники інших груп можуть вносити доповнення, спільно розв’язавши задачу всі записують її в робочий зошит.
Кожна група отримує індивідуальні завдання, на розв’язання яких має відведений час – до 10 хвилин.
Група №1 (Піфагори):
-
Розв’язати систему рівнянь:
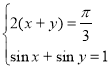 .
.
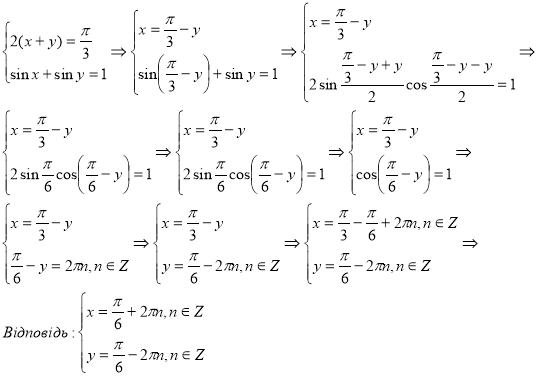
- Розв’язати нерівність:
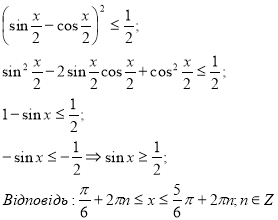
Група №2 (Декарти):
- Знайти найбільший від’ємний корінь рівняння:
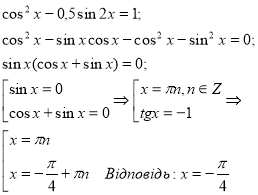 ;
;
2. Скільки коренів має рівняння ![]() на проміжку
на проміжку ![]() ?
?
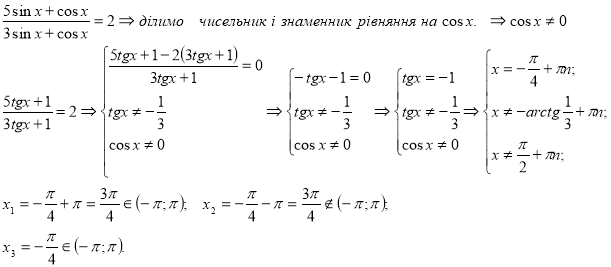 Відповідь: на проміжку
Відповідь: на проміжку ![]() рівняння має 2 корені.
рівняння має 2 корені.
Група №3 (Ньютони):
1. Розв’язати рівняння:
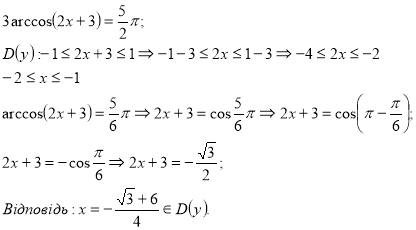
2.Знайти розв’язки рівняння ![]() на проміжку
на проміжку ![]() . Відповідь записати в градусах.
. Відповідь записати в градусах.
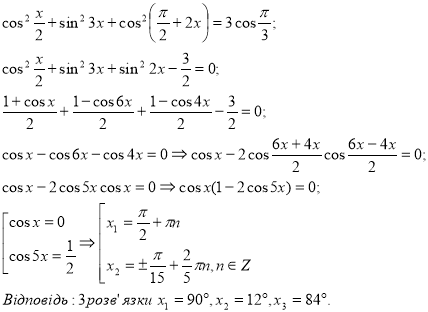
Група №4 (Лейбніци):
1. Розв’язати рівняння:
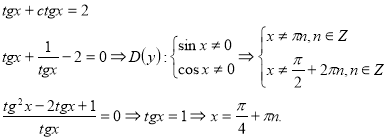
2.Знайти розв’язки рівняння ![]() на проміжку
на проміжку ![]() .
.
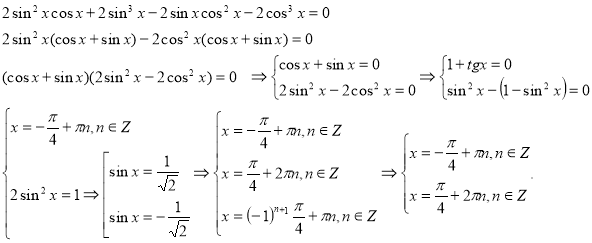 Відповідь:
Відповідь: ![]() .
.
5.Підведення підсумків уроку.
Ми узагальнили та повторили розв’язування тригонометричних рівнянь, систем рівнянь та нерівностей.
Як працювала кожна група? Які результати роботи?
Домашнє завдання: підготуватися до контрольної роботи.
Вправа №2 (27, 41), №3 (2, 4, 6).
Додатково розв’язати с-му рівнянь 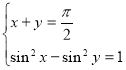
Група №1 (Піфагори):
1. Розв’язати систему рівнянь: 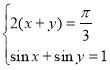 .
.
-
Розв’язати нерівність:
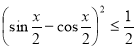 .
.
Група №2 (Декарти):
-
Знайти найбільший від’ємний корінь рівняння:
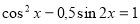 ;
;
-
Скільки коренів має рівняння
 на проміжку
на проміжку 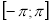 ?
?
Група №3 (Ньютони):
-
Знайти розв’язки рівняння
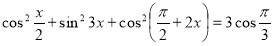 на проміжку
на проміжку 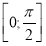 ;
;
2. Розв’язати рівняння: ![]() ;
;
Група №4 (Лейбніци):
-
Розв’язати рівняння:
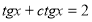 .
.
-
Знайти розв’язки рівняння
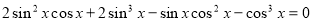 на проміжку
на проміжку 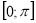 .
.
Група №1 (Піфагори):
1. Розв’язати систему рівнянь: 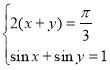 .
.
2.Розв’язати нерівність: 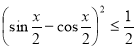 .
.
Група №2 (Декарти):
-
Знайти найбільший від’ємний корінь рівняння:
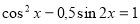 ;
;
-
Скільки коренів має рівняння
 на проміжку
на проміжку 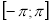 ?
?
Група №3 (Ньютони):
1.Знайти розв’язки рівняння ![]() на проміжку
на проміжку ![]() ;
;
-
Розв’язати рівняння:
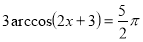 .
.
Група №4 (Лейбніци):
-
Розв’язати рівняння:
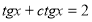 .
.
-
Знайти розв’язки рівняння
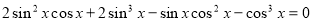 на проміжку
на проміжку 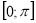 .
.
1

про публікацію авторської розробки
Додати розробку
