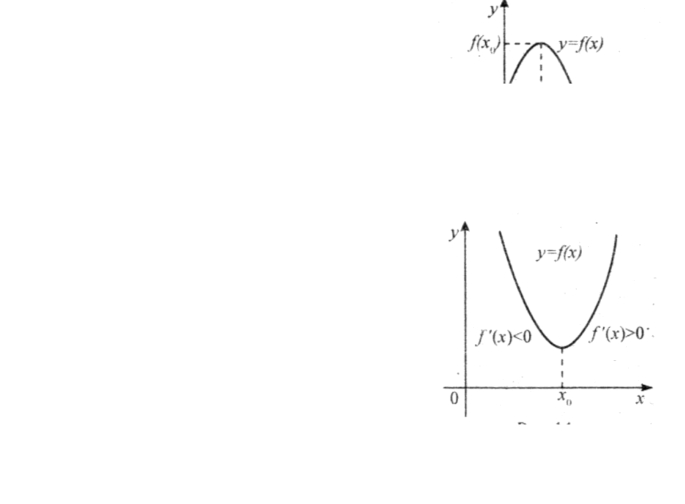науково-дослідницької роботи « Застосування похідної для розв’язування алгебраїчних задач та задач прикладного змісту»
Одним з основних розділів шкільного курсу алгебри і початків аналізу є розділ « Похідна та її застосування ». Під час вивчення цієї теми я звернула увагу на те, що застосування похідної в основному зводиться до математичних задач і частково фізичних. Тому я вирішила проаналізувати застосування похідної не тільки при дослідженні та побудові графіків функцій , а також більш прикладної спрямованості –розв'язуванні задач з економіки,біології, хімії і фізики.
Міністерство освіти і науки України
Департамент освіти і науки Вінницької обласної державної адміністрації
Вінницьке територіальне відділення МАН України
Могилів - Подільське наукове товариство «Мала Академія Наук»
|
|

|
Роботу виконала |
|
|
|
Керівник другої кваліфікаційної категорії |
ТЕЗИ
науково-дослідницької роботи « Застосування похідної для розв’язування алгебраїчних задач та задач прикладного змісту»
Автор – Петровська Анастасія, Вендичанська загальноосвітня школа І-ІІІ ступенів, гімназія, 11 клас.
Науковий керівник – Буланюк Олена Святославівна, учитель математики Вендичанської СЗШ І-ІІІ ст, гімназії, спеціаліст другої кваліфікаційної категорії.
Одним з основних розділів шкільного курсу алгебри і початків аналізу є розділ « Похідна та її застосування ». Під час вивчення цієї теми я звернула увагу на те, що застосування похідної в основному зводиться до математичних задач і частково фізичних. Тому я вирішила проаналізувати застосування похідної не тільки при дослідженні та побудові графіків функцій , а також більш прикладної спрямованості –розв’язуванні задач з економіки,біології, хімії і фізики.
Тема дослідницької роботи вибрана не випадково, оскільки застосування похідної дозволяє більш ефективно вирішувати багато завдань підвищеної складності. Застосування похідної для розв'язування задач потребує від учнів нетрадиційного мислення. Слід зазначити, що знання нестандартних методів і прийомів рішення завдань сприяє розвитку нового, нешаблонного мислення, яке можна успішно застосовувати також і в інших сферах людської діяльність. Це доводить актуальність даної роботи.
Розділ алгебри та початків аналізу “Похідна та її застосування” займає значне місце у шкільному курсі математики, в першу чергу тому, що має велике прикладне значення.
Метою даної роботи є дослідження поняття «похідна», її геометричного і механічного змісту а також застосування похідної при розв’язуванні прикладних задач та вивчення застосування похідної при розв'язування задач з алгебри і початків аналізу.
При вивченні змінюються дуже часто величини і виникає питання про швидкость. Так ми говоримо про швидкість руху літака, поїзда, автобуса, ракети, про швидкість падіння каменя, обертання шківа і т.д. Можна говорити про швидкість виконання певної роботи, про швидкість протікання хімічної реакції, про швидкість зростання населення в даному місті. Про швидкість можна говорити по відношенню до будь-якої величини, яка змінюється з часом. Для всього цього використовується поняття похідної.
Актуальність теми полягає в необхідності більш грунтовного дослідження застосування похідної при розв’язуванні прикладних задач.
Для досягнення даної мети нам необхідно було розв’язати такі завдання:
1.Дати визначення похідної ,її геометричного та механічного змісту.
2.Застосування похідної при дослідженні та побудові графіків функцій.
3.Розглянути застосування похідної при розв’язанні економічних, фізичних,
хімічних задач та задач з алгебри.
|
ЗМІСТ |
|
ТЕЗИ |
|
ВСТУП |
|
1. ПОХІДНА ФУНКЦІЇ, ЇЇ ГЕОМЕТРИЧНИЙ ТА МЕХАНІЧНИЙ ЗМІСТ. |
|
1.1. Означення похідної |
|
1.2. Фізичний зміст похідної |
|
1.3. Геометричний зміст похідної |
|
2. ЗАСТОСУВАННЯ ПОХІДНОЇ |
|
2.1. Застосування похідної до наближених обчислень |
|
2.2. Застосування похідної до дослідження функції та побудови її графіка |
|
2.3. Застосування похідної в геометрії |
|
2.4. Застосування похідної в фізиці |
|
3. ПРИКЛАДНІ ЗАДАЧІ НА ЗАСТОСУВАННЯ ПОХІДНОЇ |
|
ВИСНОВКИ |
|
СПИСКИ ВИКОРИСТАНИХ ДЖЕРЕЛ |
|
ДОДАТКИ |
ВСТУП
Математика цікава тоді,
коли живить нашу винахідливість і здатність міркувати.
Д.Пойа Виникнення математичного аналізу не випадково припадає саме на XVII
століття.
У цю епоху розвиток науки і техніки дійшов тієї межі, коли для подальшого просування вперед необхідно було більш глибоке проникнення в сутність речей,
вивчення законів природи та процесів, що відбуваються в навколишньому середовищі.
Усі ці процеси відбуваються з певною швидкістю, всі величини, що беруть участь у них, змінюються, причому у взаємозв'язках. Тому постала необхідність у такому апараті, за допомогою якого можна було б вивчати змінні процеси. Саме такий апарат і був розроблений у математичному аналізі. Тобто виникнення математичного аналізу було історично неминучим: цього вимагали потреби механіки, фізики та техніки. У свою чергу, саме ці вимоги були визначені рівнем розвитку виробничих сил суспільства. Проте повне його обґрунтування було подане лише наприкінці XIX століття.[6, ст.28]
Поняття похідної як швидкості зміни функції виникло в XVII столітті у зв'язку з потребою розв'язати деякі математичні і фізичні задачі. Великий І. Ньютон відкрив загальній спосіб обчислення швидкості по заданому шляху, з допомогою цього способу для кожної функції s можна побудувати нову функцію v. Цю функцію називають похідною функції s, а сам перехід від функції s до функції v -
диференціюванням.
Відкриття Ньютона явилось поворотним пунктом в історії природничих наук.
Виявилось, що кількісні характеристики різних процесів, які досліджуються у фізиці, хімії, біології, в технічних дисциплінах можуть бути подані на мові математичного аналізу, що вивчає зв’язок між функціями і їх похідними.
Важливою і найпростішою моделлю для побудови похідної залишається модель, вивчена І. Ньютоном — модель механічного руху. В цій моделі початковою функцією є шлях, її похідною — швидкість. Тому найпростіша відповідь на питання, що таке похідна є відповідь, похідна — це швидкість. Результати своїх досліджень Ньютон виклав у трактаті «Метод функцій нескінченних рядів»,
опублікованому 1736 року. [1,ст.149]
Одночасно з Ньютоном до поняття похідної прийшов німецький математик Лейбніц, вивчаючи дотичні до довільних кривих.
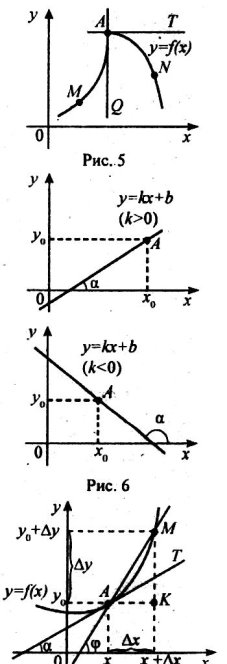
Як пов’язані між собою задачі знаходження швидкості і побудови дотичної?
Накреслимо графік залежності шляху s від часу t. Допустимо, спочатку, що на протязі певного проміжку часу рух рівномірний. Тоді відповідна ділянка матиме вигляд відрізку деякої прямої l. Швидкість при цьому постійна, вона дорівнює кутовому коефіцієнту прямої l. А з іншого боку пряма l і буде дотичною до графіка руху в точках даного відрізку. В першому підручнику по математичному аналізу, що був написаний 300 років тому, учнем Лейбніца маркізом Лопіталем було сказано:
якщо продовжити одну із ланок MN кривої, що складаю криву лінію, то продовжена таким чином сторона буде називатися дотичної до кривої в точці M чи N.
Рис. 1 Рис. 2
На цьому маленькому відрізку швидкість руху постійна і рівна кутовому коефіцієнту прямої MN. Отже, швидкість рівна кутовому коефіцієнту дотичної до графіка шляху. [2,ст.51-53]
Таким чином, актуальність теми полягає в необхідності більш грунтовного дослідження застосування похідної при розв’язуванні прикладних задач.
Об'єктом дослідження наукової роботи є прикладні задачі, під час розв’язування яких використовується похідна.
Предметом дослідження є застосування похідної при розв'язуванні задач з математики,хімії, фізики, економіки.
Дане дослідження виходить з тези « математику треба вчити так, щоб вміти її застосовувати».
Методи дослідження обумовлені поставленими в роботі науковими цілями й завданнями. Я використовувала прийоми аналізу ,порівняння,узагальнення.
Наукова новизна роботи полягає у тому, що в ній розглянуто практичне застосування похідної під час розв’язування задач з фізики ,хімії,біології,економіки.
Практичне значення дослідження полягає у тому, що його висновки та основні твердження можна використовувати для поглибленого вивчення теми
«Похідна». Зважаючи на важливу роль прикладних задач сприяє посиленні мотивації вивчення похідної а також формуванні в учнів здатностей застосування знань при вивченні інших предметів. Матеріали та результати роботи можуть бути використані при підготовці до ЗНО, а також для факультативних занять .
РОЗДІЛ 1. ПОХІДНА ФУНКЦІЇ, ЇЇ ГЕОМЕТРИЧНИЙ ТА ФІЗИЧНИЙ
(МЕХАНІЧНИЙ) ЗМІСТ
1.1. Означення похідної
Нехай задано функцію у=f(х) на деякому проміжку. Візьмемо довільну внутрішню точку x0 цього проміжку, надамо значенню х0 довільного приросту ∆х
(число ∆х може бути як додатним, так і від’ємним), але такого, щоб точка х0+∆х
належала даному проміжку.
Тоді:
1) обчислимо в точці х0 приріст ∆у = ∆f(х0) функції:
∆у = ∆f(х0)= ∆у = f(х0+∆х)- f(х0);
х
2) складемо відношення
3) Знайдемо границю цього відношення за умови, що ∆х→0, тобто:
|
lim |
y |
lim |
f ( x0 ) |
lim |
f ( x0 x ) f ( x0 ) |
. lim |
y |
lim |
f ( x0 ) |
lim |
f ( x0 x ) f ( x0 ) . |
|
x 0 |
x |
x 0 |
x |
x 0 |
x |
x 0 |
x |
x 0 |
x |
x 0 |
x |
Якщо дана границя існує, то y називають похідною функції у=f(х) у точці х0 і
позначають f'(х0) або y'.
Похідною функції у=f(х) у точці х0 називають границю відношення приросту функції до приросту аргументу за умови, що приріст аргументу прямує до нуля, а
границя існує, тобто:
|
f '( x ) lim y |
lim f ( x0 x ) f ( x0 ) . |
|||
|
0 |
x 0 |
x |
x 0 |
x |
|
|
||||
Функцію, яка має похідну в точці х0, називають диференційованою в цій точці. Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням.
Нехай D1 — множина точок, у яких функція у=f(х) диференційована. Якщо кожному поставити у відповідність число f'(х), то одержимо нову функцію з областю визначення D1. Цю функцію позначають f':
|
f '( x) lim |
f ( x0 x ) f ( x0 ) |
. [8,ст.159] |
|
x 0 |
x |
|
|
|
|
|
|
||||
|
Нехай матеріальна точка М рухається |
|
|
|
|
|||
|
прямолінійно за законом s=f(t) «рис. 1.2.1». |
|
|
|
|
|||
|
У момент t0 вона зайняла положення |
|
|
|
|
|||
|
Мо і пройшла |
шлях s0=f(t0). |
Знайдемо |
|
|
|
|
|
|
швидкість точки в момент t0. |
|
|
«Рис. 1.2.1» |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||
|
Припустимо, що за довільно вибраний проміжок часу ∆t, починаючи з |
|||||||
|
моменту t0, точка перемістилася на відстань ∆s і зайняла положення М1. |
|
|
|
||||
|
Тоді t1 = t0 + ∆t , s1=f(t1)=s0+∆s. |
|
|
|
|
|||
|
За проміжок часу ∆t матеріальна точка проходить шлях |
|
|
|
||||
|
|
∆S = f(t1)-f(t0) = f(t0+∆t) – f(t0), |
|
|
|
|
||
|
Середня швидкість (vсер.) руху на проміжку M0M1 дорівнює |
|
|
|
||||
|
Якщо ∆t |
наближається |
до нуля, то середня швидкість |
|
буде |
|||
|
|
|||||||

наближатися до швидкості в момент t0.
Миттєвою швидкістю точки, яка рухається прямолінійно, у момент часу t0
називають границю середньої швидкості за умови, що ∆t наближається до нуля:
|
v |
|
lim v |
lim s lim |
f (t 0 t ) f (t0 ) |
. |
|
|
ì èò . |
|
|||||
|
|
t 0 |
ñåð. |
t 0 tt0 |
t |
||
|
|
|
|
||||
Числа ∆t , ∆s називають відповідно приростом часу і приростом шляху.
Отже, миттєвою швидкістю точки, яка рухається прямолінійно, є границя відношення приросту шляху ∆s до відповідного приросту часу ∆t, коли приріст часу наближається до нуля.
Висновок: якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом s=s(t), то швидкість її руху v(t) у момент часу t дорівнює похідній s'(t): v(t)= s'(t).
1.3. Геометричний зміст похідної

Для введення означення дотичної до кривої
розглянемо функцію у=f(х) і її графік — криву лінію
«рис. 1.3.1». Нехай точки А і М належать графіку функції у=f(х), проведемо січну АМ.
Зафіксуємо точку А. Нехай точка М,
рухаючись по кривій, наближається до А. При цьому
січна АМ буде повертатися навколо точки А і в
«Рис. 1.3.1»
граничному положенні при наближенні точки М до
точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А.
|
Дотичною АТ до графіка функції у=f(х) в |
|
|||||
|
|
|
|||||
|
коли точка М, рухаючись по кривій, наближається до |
|
|||||
|
точки А. |
|
|
|
|
|
|
|
Слід мати на увазі, що не в усякій точці кривої |
|
|||||
|
можна провести |
до |
неї |
дотичну. |
На |
рис.«1.3.2» |
|
|
«Рис. 1.3.2» |
||||||
|
|
|
|
|
|
|
|
|
зображено криву |
у |
=f(х), |
яка в |
точці |
А не має |
|
|
|
||||||
дотичної, бо якщо точка М буде наближатися до точки А по лівій частині кривої, то січна МА займе граничне положення АQ.
Якщо точка N буде наближатися по правій частині кривої, то січна NА займе граничне положення АТ. Одержуємо дві різні прямі АQ і АТ. Це означає, що в точці
А до даної кривої дотичної не існує.
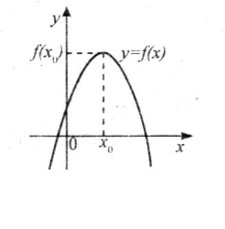
Поставимо задачу: провести дотичну до графіка функції у=f(х) у точці
А(х0;y0).
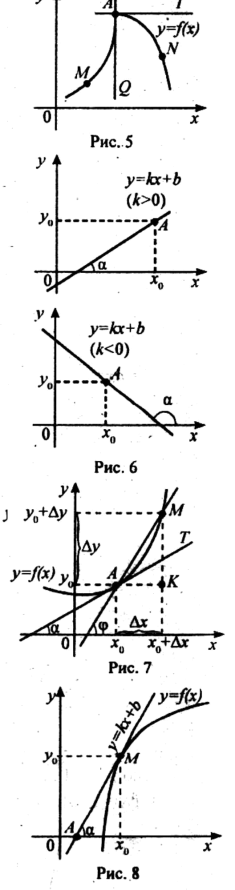
Дотична — це пряма, а положення прямої у=kх+b, яка проходить через точку
А(х0;y0), визначається кутовим коефіцієнтом прямої k=tg , де — кут між прямою і додатним напрямом осі ОХ (рис. 1.3.3).
Отже, провести дотичну до графіка означає знайти число k.
Нехай у точці А(х0;y0) «рис. 1.3.4» кривої у=f(х)
існує дотична, визначимо кутовий коефіцієнт дотичної. Для цього:
- надамо аргументу х0 приросту ∆х, одержимо нове значення аргументу х0+∆х;
- знайдемо відповідний приріст функції
∆у=f(х0+∆x)-f(x0);
|
3) знайдемо відношення |
|
|
|
х |
|
. Із |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
трикутника |
AMK |
маємо |
Y |
tg MAK . |
Оскільки |
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«Рис. 1.3.3» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Ì ÀÊ — куту |
нахилу |
січної АМ |
із |
Додатним |
|
|
|
||||||||||||
|
напрямом осі ОХ, то — |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4) якщо ∆х→0, то ∆у→0, і точка М буде |
|
|
|
||||||||||||||||
|
переміщуватися по кривій, наближаючись до точки А. |
|
|
|
||||||||||||||||
|
При цьому січна АМ буде повертатися навколо |
|
|
|
||||||||||||||||
|
точки А, а |
величина |
|
кута |
ф буде змінюватися зі |
|
|
|
||||||||||||
|
зміною ∆х. Граничним положенням січної |
АМ при |
|
|
|
Рис. 1.3.4 |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
∆х→0 буде дотична АТ, яка утворює з додатним |
|
|
|
||||||||||||||||
|
напрямом осі ОХ деякий кут, величину якого |
|
|
|
||||||||||||||||
|
позначимо через . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, |
lim |
y |
lim tg tg k |
— |
Кутовий |
|
|
|
|||||||||||
|
|
x 0 |
x |
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коефіцієнт дотичної. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Порівнюючи одержані результати з означенням |
|
|
|
|
|||||||||||||||
|
|
«Рис. 1.3.5» |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
похідної, можна зробити висновок: значення похідної |
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||
|
функції ∆у=f(х) у точці х0 |
дорівнює кутовому коефіцієнту дотичної до графіка |
||||||||||||||||||
|
функції в точці з абсцисою х0: |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
f'(x0)=k |
|
(рис. 1.3.5). |
|
|
|
|||||||
Функція у=f(x) називається нескінченно малою, якщо lim f ( x) 0 .
x a
( x)
Якщо функція y=f(x) має похідну в точці х0, то за означенням:
f '( x0 ) lim f ( x0 )
x 0 x
Адже тоді функція
|
h ( x ) |
f ( x0 ) f '( x ) |
(1) |
|
|
|
x |
0 |
|
|
|
|
|
|
|
є нескінченно малою при x 0 , тобто |
|
|
|
|
lim h( x ) 0 |
|
|
|
|
x 0 |
|
|
|
|
З рівності (1) випливає, що |
|
|
|
|
f ( x0 ) f '( x ) h ( x) |
|
||
|
x |
0 |
|
|
|
|
|
|
|
|
або |
|
|
|
|
f ( x0 ) f '( x0 ) x h( x ) x |
(2) |
||
Так, як h( x ) x нескінченно мала функція вищого порядку порівняно з x ,
то маємо
f ( x0 ) f '( x0 ) x
Застосовуючи цю формулу можна вивести наближену формулу для знаходження за якою обчислюються наближені значення коренів з чисел
n x
![]()
n x0 x n x0 ![]() 0x[9,ст.3], [11,ст.93](x0).n x0
0x[9,ст.3], [11,ст.93](x0).n x0
![]()
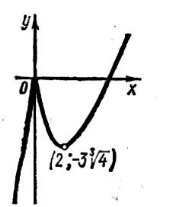
Приклади. Обчислити наближене значення коренів
|
а) |
|
|
|
|
; б) 6 |
|
|
; в) |
|
|
. |
|
|
|
|
|||||
|
5 |
32, 48 |
|
63,894 |
9, 02 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання |
||
|
|
|
|
|
|
|
|
|
5 |
|
0.48 |
|
|
2 0, 48 |
|
||||||
|
а) |
5 |
|
5 |
|
|
5 |
|
|
32 |
2 |
2 0, 006 2, 006 |
|||||||||
|
32, 48 |
32 0, 48 |
32 |
||||||||||||||||||
|
|
5 32 |
5 32 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
![]()
![]()
Відповідь: 2,006
13
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
6 |
|
|
|
6 |
|
|
6 |
|
|
6 64 |
|
0,106 2 0, 0006 1, 9994 |
||||
|
63,894 |
64 0,106 |
64 |
|||||||||||||||
|
6 64 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Відповідь: 1,9994 |
|
|
|
|
|
|
||||||||
|
в) |
|
|
|
|
3 |
3 |
0, 02 3 0, 033 3, 0033 |
||||||||||
|
9, 02 |
9 0, 02 |
||||||||||||||||
|
|
2 9 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
![]()
![]()
Відповідь: 3,003
![]() 2.2. Застосування похідної до дослідження функції на побудови її графіка
2.2. Застосування похідної до дослідження функції на побудови її графіка
У курсі математичного аналізу похідна застосовується, як правило, з метою:
- Дослідження функцій на монотонність.
- Дослідження функцій на екстремум.
- Знаходження найбільших і найменших значень функцій.
- Дослідження їх на опуклість, угнутість та знаходження точок перегину. (див. додаток А,Б)
|
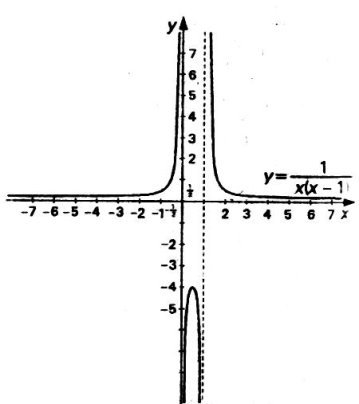
Приклад. Дослідити функцію y = |
|
і побудувати графік |
|
|
|
|
||
|
1) Область визначення: x ≠ 0, x ≠ 1. D( y ) = ( -∞; 0 ) ( 0; 1 ) |
( 1; +∞ ). |
||
- Дана функція не є ні парною, ні непарною, неперіодична.
- Точки перетину з осями координат та проміжки знакосталості функції з віссю Оу точок перетину немає, бо х ≠ 0. Тоді у ≠ 0, тобто з віссю Ох точок перетину також немає. Визначимо знак функції на D(у).

Отже, функція додатна, якщо х є (-∞; 0) та x є (1; +∞), функція від’ємна,якщо
- є (0; 1) .
- Похідна та критичні точки. y' (x)=
![]()
![]()
y' (x) = 0; 2x – 1 = 0; x = . y' (x) не існує в точках x = 0 і x= 1.
![]()
5) Інтервали монотонності та точки екстремуму:
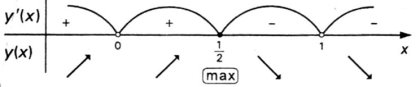
y .
![]()
6) Розглянемо функцію на кінцях області визначення і знайдемо асимптоти.
Якщо х 0 зліва, то у(х)
![]()
Якщо х 0 справа, то у(х)
![]()
Якщо х 1 зліва, то у(х)
![]()
Якщо х 1 справа, то у(х)
![]()
Отже, вертикальні асимптоти — х = 0тах = 1.
Оскільки , то у = 0 - горизонтальна асимптота.
![]()
7) Друга похідна, напрям опуклості, точки перегину.
Y
![]()
![]()
![]()
|
y |
≠ 0, бо |
≠ 0 (D = 9 – 12 = - 3), причому |
> 0. |
|
Знак другої похідної змінюється в точкахx =0 i x = 1. |
|
||
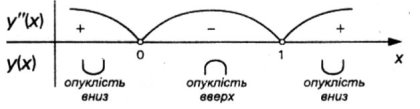
|
8) |
Контрольні точки. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
- 1 |
|
|
|
|
|
2 |
|
|||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
9) |
Побудуємо графік функції. |
|
|
|
|
|
|
|||||||
2.3. Застосування похідної в геометрії
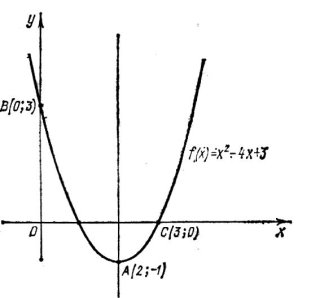
Приклад 1. Знайти кутовий коефіцієнт дотичної до параболи y x2 3 в точці
x 12
![]()
Розв’язання
- Знаходимо похідну заданої функції y ' 2 x .
- Для знаходження кутового коефіцієнта дотичної до параболи в точці з
абсцисою x 12 підставляємо це значення в y ' :
![]()
- ' 1 1, тобто tg 1.
- 2
![]()
Кутовий коефіцієнт дотичної дорівнює 1. 3) Якщо tg 1 450 .
Відповідь: k 1
Приклад 2. Записати рівняння дотичної до графіка функції в точці
|
f ( x) |
1 |
2 з абсцисою |
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Розв’язання |
|
|
|
|||||||
|
|
Оскільки f '( x) |
4 |
|
, то кутовий коефіцієнт дотичної в точці |
x |
дорівнює |
|||||||||||
|
|
|
x5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
f '( x ) |
4 |
|
|
4 |
|
4 , |
|
|
|||
|
|
|
|
|
|
|
x5 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
15 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y f ( x ) |
|
1 |
2 3 . |
|
|
||||||
|
|
|
|
|
|
|
14 |
|
|
|||||||||
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|||
 Підставляючи ці значення в рівняння дотичної y y0 f '( x0 ) ( x x0 ) ,
Підставляючи ці значення в рівняння дотичної y y0 f '( x0 ) ( x x0 ) ,
дістанемо
y 3 4 ( x 1) 4 x 7 .
Відповідь: Рівняння дотичної y 4 x 7
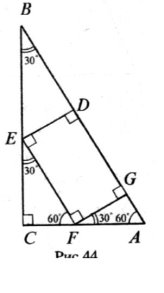
Приклад 3. У прямокутний трикутник з гіпотенузою
24 см і кутом 60 ° вписано прямокутник, основа якого лежить на гіпотенузі. Якими мають бути довжини сторін прямокутника, щоб його площа була найбільшою? [4,ст.416]
«Рис.2.3.1»
Розв’язання
Нехай прямокутник DEFG вписано в трикутник ABC «Рис. 2.3.1». Оскільки
BA=24 см, то АС=12 см як катет, що лежить проти кута 30°. Нехай DG=EF=x (0<x<24).
Тоді у CEF CF= 2x ; далі FA=CA-CF=12- 2x .
![]()
![]()
У FGA маємо
![]()
FG=FA sin 60 0 ![]() 23 (12 2x) .
23 (12 2x) .
![]()
![]()
Площа прямокутника DEFG
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
S DEFG S ( x ) |
|
3 |
x (12 |
x |
) 6 |
|
x |
3 |
, |
|||
|
|
3 |
|||||||||||
|
|
|
|
4 |
|||||||||
|
|
2 |
2 |
|
|
|
|
||||||
![]()
![]()
![]()
![]()
S '( x ) 6![]()
![]() 3 23 x ,
3 23 x ,
![]()
![]()
S ' 0 , якщо x 12 . Розставимо знаки похідної «рис 2.3.2». Отже, x 12 — точка максимуму. Тоді умові задачі задовольняють
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
(12 |
|
12 |
) 3 |
|
|
|
|||
|
|
|
3 |
|
|||||||||
|
сторони 12 см і 2 |
|
2 |
см. |
|||||||||
|
|
|
|
|
|
|
|
||||||
|
Відповідь: 12 см і 3 |
|
см |
|
|||||||||
|
3 |
|
|||||||||||
![]()
![]()
«Рис 2.3.2»
2.4. Застосування похідної в фізиці
Задачі що приводять до поняття похідної.
Нехай з міста А до міста В рухається автомобіль. Відстань між містами дорівнює Sкм. і автомобіль проходить її за T годин.
Якби автомобіль рухався рівномірно, тобто проходив однакову відстань за однакові проміжки часу незалежно від того, на які ділянці шляху він знаходиться, то за означенням, швидкість руху автомобіля дорівнювала б відношенню довжини шляху до часу за який пройдено цей шлях:
Припустимо тепер, що рух не рівномірний. Тоді справа з означенням швидкості зразу стає набагато складнішою. Відношення характеризує тільки так звану “середню швидкість” і майже зовсім не дає інформації про те, як саме рухається автомобіль. Справді, середня швидкість є стала величина, що не змінюється з часом, а “реальна швидкість” руху автомобіля різна в різні моменти часу.
Ми звикли до інтуїтивного поняття швидкості. Всі розуміють таку фразу: “спочатку автомобіль стояв, потім почав рухатись, і швидкість його руху поступово зростала”. Але це означає, що ми маємо на увазі не деяку середню швидкість, а швидкість руху в кожний момент часу. Але як дати строге з точки зору математики означення цієї “миттєвої швидкості”? Можна підійти до цієї справи так.
Позначимо через S(t) – відстань, яку пройде автомобіль за час t від початку руху. Якщо в момент t автомобіль знаходився в деякій точці Е, то в момент часу t+∆t він буде знаходитись в деякій інші точці Е’, що знаходить на відстані S(t+∆t) від початкової. Тоді це означає що за час ∆t автомобіль пройшов відстань S(t+∆t)-S(t)=∆S. Середня швидкість на цьому проміжку часу [t, t+∆t] дорівнюватиме відношенню
Якщо зменшувати ∆t, то дістанемо середню швидкість на все меншому проміжку часу, який починається з t, і тому природно називати швидкість руху в момент часу t
Означення похідної
З фізичної точки зору похідна є швидкість зміни характеристики деякого фізичного процесу, коли ця характеристика змінюється з часом.
Означення. Якщо в кожній точці проміжку Х існує похідна f’(x), то її називають похідною функції від функції f(x), або просто похідною від f(x) (на проміжку Х).
Похідну часто позначають ще так: , ніби вона є відношення деяких величин df(x) та dx.
На основі цього означення можна сказати, що швидкість V(t) руху тіла є похідна від функції S(t) – шляху, який пройшло тіло за час t.
Всім добре відоме фізичне поняття прискорення. З ним пов’язана, наприклад, поняття рівномірного руху, рівноприскореного руху. У випадку з прискоренням ми повинні знайти таку характеристику руху, яка б відображала “швидкість зміни швидкості руху”, тобто якщо швидкість з часом зростає – прискорення повинно збільшуватися, в будь-якому випадку бути додатним; якщо швидкість стала – прискорення не повинно бути, або точніше, воно повинно дорівнювати нулю; якщо швидкість спадає, то прискорення від’ємне. Позначивши через V(t) швидкість в момент часу t, введемо поняття середнього прискорення на проміжку від t0 до t0+∆t як відношення
приросту швидкості на цьому проміжку до довжини проміжку. Отже, строгим означенням прискорення руху тіла є таке:
Прискорення в момент часу t0 називається границя
якщо вона існує, де V(t) – швидкість руху в момент часу t.
Таким чином, прискорення є похідна швидкості.
a(t)=V’(t), або .
а) Закон вільного падіння.
Запишемо закон вільного падіння:
Для середньої швидкості падіння в проміжку часу (t, t+∆t) маємо
а для швидкості в момент t
Звідси видно, що швидкість вільного падіння пропорційна часу руху (падіння).Застосування похідної в фізиці розглянемо на прикладі таблиці
|
|
Функція |
Миттєва швидкість зміни функції |
|
|
|
|
|
|
|
1. |
S = S (t) – шлях, який проходить тіло |
r = S' (t), [м/ ] |
|
|
|
за час t; [м] |
|
|
|
|
|
|
|
|
2. |
r = r (t) = швидкість нерівномірного |
a = r'(t) - прискорення, [м/ |
|
|
|
руху тіла, де t – час; [м/ ] |
|
|
|
|
|
|
|
|
3. |
q = q(t) – кількість електрики, яка |
I = q'(t)сила струму, [А] |
|
|
|
проходить через |
поперечний переріз |
|
|
|
провідника за час t ; [Кл] |
|
|
|
|
|
|
|
|
4. |
С – кут повороту тіла за час t; |
– кутова швидкість, [ ад/ ] |
|
|
|
[ ад] |
|
|
|
|
|
|
|
|
5. |
m = m (l) – ма а будь-якої ча тини |
p = m' (l) лінійна густина стержня, [г/ м] |
|
|
|
н одно ідного т |
жня завдовжки l; |
|
|
[ г ] |
|
|
|
|
|
|
|
|
|
6. |
А = А (t) – робота, яка здійснюється у |
W = A'(t)- потужність, [Вт] |
|
|
|
момент часу t; [Дж] |
|
|
|
|
|
|
|
|
7. |
Q = Q (T) – кількість теплоти, яку |
С= Q’ (T) – питома теплоємність |
|
|
|
необхідно надати тілу, щоб змінити |
речовини даного тіла, [Дж] |
|
|
|
його температуру на T градусів; [Дж] |
|
|
|
|
|
||
|
8. V = V (t) – обсяг випуску продукції за |
f = V' (t) - продуктивність праці за час t |
||
|
|
проміжок часу t; [одиниці п одукції] |
|
|
|
|
|
|
|
Розв’яжемо фізичні задачі на знаходження сили, яка діє на тіло в момент часу, сили струму,кутову швидкість .
Приклад 1. Матеріальна точка масою 4кг рухається прямолінійно по закону
S (t ) 4t t 2 16 t3 (м). Знайти силу, яка діє на неї в момент часу t 2 (с).
![]()
Розв’язання Так, як F ma , то знаходимо прискорення:
- v S '(t ) 4 2t 12 t 2
- a v '(t ) S ''(t ) 2 t , при t 2 , a 0
![]()
Відповідь: F 0
Приклад 2. Кількість електроенергії, що проходить через провідник,
починаючи з часу t 0 задається формулою Q 3t 2 3t 4 (Кл). Знайти величину сили струму в кінці 6-ї секунди.
Розв’язання Сила струму є похідна від кількості електрики по часу, отже, потрібно знайти
похідну заданої функції Q 3t 2 3t 4 і обчислити її значення при t 6 . Маємо
I Q ' 6t 3 .
Якщо t 6 , I 33 А.
Відповідь: I 33 А.
Приклад 3. Маховик, що затримується гальмом, за t с повертається на кут
5t 0, 4t2 рад. Знайти кутову швидкість W (t) маховика в момент часу t 2 с і
обчислити момент зупинки руху.
Розв’язання
Кутова швидкість W (t) в момент часу t с ( t час до зупинки) дорівнює
W (t ) ' 5 0,8t рад/с, отже, W (2) 5 1, 6 3, 4 (рад/с).
Обертання закінчиться, коли W (t ) 0 , тобто 5 0,8t 0 t 6, 25 с
Відповідь: W (2) 3, 4 (рад/с), t 6, 25 с.
РОЗДІЛ 3. ПРИКЛАДНІ ЗАДАЧІ НА ЗАСТОСУВАННЯ ПОХІДНОЇ
Приклад 1. Капітал у 1 млрд. грош. одиниць може бути розміщено у банку під 50% річних або інвестований у підприємство, при цьому ефективність вкладу очікується у розмірі 100%, а витрати задані квадратичною залежністю. На прибуток накладається податок в %. При яких значеннях вклад в підприємство є більш ефективним, ніж чисте розміщення капіталу у банку?
Розв’язання.
Нехай x (млрд. грош. одиниць) інвестується в підприємство, а (1–x)
розміщується під відсотки. Тоді розміщений капітал через рік дорівнюватиме
|
|
|
50 |
|
|
|
|
3 |
|
|
3 |
|
|
|
|
1 x 1 |
|
|
|
|
|
|
|
|
|
|
x |
, а капітал, вкладений в підприємство, визначимо за |
|
|
|
|
|
2 |
2 |
|||||||||
|
|
|
100 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
100 |
|
|
|
||||
|
формулою x 1 |
|
|
|
|
|
|
2x . |
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
100 |
|
|
|
||||
|
|
|
|
Витрати будуть складати аx2 |
, оскільки за умовою вони задаються |
||||||||||||||||||||||||||||||
|
квадратичною залежністю, тобто прибуток від вкладу в |
підприємство =2x-ax2. |
|||||||||||||||||||||||||||||||||
|
Податки |
складають |
2x ax2 |
p |
, тобто |
чистий |
прибуток |
буде |
дорівнювати |
||||||||||||||||||||||||||
|
100 |
||||||||||||||||||||||||||||||||||
|
|
|
p |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2x ax |
|
. Загальна сума через рік складатиме |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
p |
|
2 |
|
|
3 |
|
|
|
|
p |
|
3 |
|
|
|
p |
|
2 |
|
|||
|
|
|
|
|
A( x ) |
|
|
|
x 1 |
|
|
|
2 x ax |
|
|
|
2 |
1 |
|
|
|
|
|
x a 1 |
|
|
|
x |
|
. |
|||||
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
100 |
|
100 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
Відповідно наша економічна задача зводиться до математичної задачі знаходження максимального значення цієї функції на відрізку [0, 1].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
2 1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
3 |
|
|
|
|
|
|
100 |
2 |
|
|
||||||||||||||||
|
Маємо |
|
A '( x ) 2 |
1 |
|
|
|
2 a |
1 |
|
|
x . |
A '( x) 0 при x |
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
p |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|||||
|
A '( x ) 2 a |
1 |
|
|
p |
0 , тобто x |
|
|
- точка максимуму. Щоб |
x [0;1] |
, необхідно виконати |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
умову 0 |
|
|
|
|
|
p |
|
3 |
|
|
|
|
або |
|
p 25 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
100 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким чином, якщо p < 25, то вигідніше нічого не вкладати у підприємство та розмістити весь капітал у банку. Якщо p < 25, то можна показати, що при x=x0
|
|
|
|
|
|
|
|
p |
|
|
3 2 |
|
|
|
||
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
100 |
2 |
|
3 |
|
|||||||||
|
A( x ) |
|
|
|
|
|
|
|
A(0) , тобто вклад в підприємство є вигіднішим ніж |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
2 |
|
|
|
|
|
|
|
p |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
4 a 1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
100 |
|
|
|
|
|
||||
чисте розміщення під відсотки.
Розглянемо задачу на знаходження швидкості зростання популяції особин . Нехай, Р = Р (t) – чисельність популяції в момент часу t; [о оби], тоді V = Р'(t) – швидкість зростання популяції.
Приклад 2. Розмір популяції комах у момент часу t (в днях) задається формулою
p (t) 105 9 104 . Знайдіть швидкість зростання популяції у момент t=5 днів.
![]() t 1
t 1
Розв’язання.
Швидкість зростання популяції є похідною від чисельності популяції, тобто
|
v (t ) p '(t ) . Отже, v (t) |
9 104 |
– швидкість приросту популяції комах в момент часу t. |
|||||
|
(t 1)2 |
|||||||
|
|
|
|
|
|
|
|
|
|
Тому, якщо t=5 днів, то v(5) |
9 10 4 |
|
104 |
2500 . |
|||
|
(5 1) 2 |
|
4 |
|||||
|
|
|
|
|
|
|||
Відповідь: Швидкість зростання популяції — 2500.
Приклад 3. При якій кислотності сума гідроген-іонів H+ і гідроксид-іонів OH-
в одиниці об’єму води буде найменшою?
Розв’язання.
Введемо позначення: x – концентрація гідроген-іонів H+, y – концентрація гідроксид-іонів OH-. Пригадаємо хімічний закон: xy=k, де k – стала для води (при
25oC k =10-14). Задача зводиться до знаходження найменшого значення функції
|
u x y x |
k |
. Продиференціювавши функцію |
u ( x ) x |
k |
, |
знаходимо: |
u '( x) 1 |
k |
. |
|
|
x |
x |
|
||||||||
|
|
|
|
|
|
|
|
x2 |
|||
|
u '( x) 0 . Оскільки x>0, |
то функція має єдину стаціонарну точку на всій області |
|||||||||
визначення. Знайшовши другу похідну u ''( x) 2xk3 та її значення в стаціонарній точці
![]()
|
|
|
|
|
|
|||||
|
u ''( |
|
) |
2 |
|
|
0 , на основі достатньої умови існування екстремуму функції робимо |
|||
|
k |
|||||||||
|
|
|
|
|||||||
|
|
|
|
|
K |
|||||
|
висновок, |
що точка x |
|
є точкою мінімуму. Завдяки єдиності стаціонарної точки |
||||||
|
k |
|||||||||
![]()
![]()
![]()
функція u(x) досягає в ній найменшого значення. За згаданим законом y ![]()
![]() k . Отже,
k . Отже,
![]()
сума іонів води буде найменшою, якщо концентрація іонів H+ і OH- будуть рівні між собою, тобто при нейтральній реакції (x=y=\[\sqrt{k}\]).
Приклад 4.При виверження вулкану камені гірської породи викидаються
перпендикулярно вгору з початковою швидкістю 120 м / с. Якої найбільшої висоти досягне каміння, якщо опором вітру знехтувати?
|
|
|
|
Розв'язання |
|
|
|
Речовина викидається перпендикулярно вгору. Висота каменя h, функція |
|||
|
часу - |
|
|
(1)Знаходимо похідну: |
.Отже, 120-9,8t=0, |
|
|
|
|||
тобто t ≈ 13 сек. Тоді, підставивши у 1 формулу маємо, що h = 745м.
Отже,камені гірської породи досягають рівня 720 м від краю вулкана.
ВИСНОВКИ
Сучасна школа поступово переорієнтовується на вивчення предметів на застосування знань у практичних, життєвих ситуаціях. Тому посилення прикладної спрямованості навчання математики, особливо у старшій школі, яка є зв’язуючою ланкою між середньою та вищою освітою, є актуальною та важливою проблемою.
Одним з основних розділів шкільного курсу алгебри і початків аналізу є розділ « Похідна та її застосування». Цей розділ має як систему внутрішньо-
предметних так і систему міжпредметних зв’язків. Така спрямованість навчання математики найбільше реалізується під час розв’язування прикладних задач з теми « Похідна».
Залучення учнів до розв’язування прикладних задач на уроках алгебри сприяє свідомому, якісному засвоєнню навчального матеріалу, активізує навчально
-пізнавальну діяльність, створює умови для творчої самореалізації у процесі навчання.
Проведене дослідження дає можливість учням поряд із набуттям математичних компетентностей засвоювати факти суміжних предметів, тобто бути засобом здійснення міжпредметних зв’язків. Прикладні задачі, під час розв’язування яких використовується похідна, можна знайти у підручниках і посібниках з економіки, біофізики, біохімії.
Традиційно практичне застосування похідної курсі математичного аналізу, як правило,проводиться з метою:
- Дослідження функцій на монотонність.
- Дослідження функцій на екстремум.
- Знаходження найбільших і найменших значень функцій.
- Дослідження їх на опуклість, угнутість та знаходження точок перегину.
Але роль похідної в моделюванні економічних, фізичних,хімічних процесів
розглядається, на мою думку недостатньо.
Слід зазначити, що дане дослідження не є кінцевим і повністю не розв’язує визначеної теми, а тому вимагає подальших досліджень. Вважаю, що даний матеріал може бути з використаний вчителями математики,учнями.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
- Авраменко М. І. Уроки алгебри і початку аналізу в 10 – 11 класах: Посібник для вчителя. – К. : Рад. Шк., 1989. – 320с.
- Башмаков М. И. Математика: Эксперимент учеб. пособие для СПТУ – М. : Высш. шк., 1987. – 463с. : ил.
- Богомолов Н. В. Практическое занятие по математике : Учеб. Пособие для техникумов. – 2-е изд., перераб. – М. : Высш. школа., 1983. – 399с.
- Збірник задач з математики для вступників для вузів : Тир з рос / В. К. Єгерев,
В. В. Зайцев, Б. А. Корделівський та ін. / за ред. М. Ш. Сканаві. : - К. : “Онікс”,
2005. – 608с.
- Лященко М. Я. Похідна та її застосуваня : Посібник для самоосвіти вчителів. = К. : Рад. шк., 1985. – 152с.
- Науково – медичний журнал матем. в школах України видавнича група “Основа” листопад 2013р. № 31 (403 ) ст. 28 (Желтуха Т. В. Застосування похідної до розв’язування задач)
- Новий довідник : Математика. Фізика. – К. : ТОВ “КАЗКА”, 2004. – 864с.
- Роганін О. М. Математика : навч. посіб. / О. М. Роганін. – К. : Український центр підготовки абітурієнтів, 2014. – 384с.
- Розработка уроков темы “Применение производной” в курсе математики Сруник ПТУ” методические рекомендации М. : Высш. Школо, 1979. – 32с.
10. Сімонова Н. Д. Помічник з алгебри та початків аналізу. Довідеик з алгоритмами розв’язування задач. – Х. : Вид. група “Основа”, 2004. – 192с.
11. Слєпкань З. Ш. Методика викладання алгебри і початків аналізу. К., Рад. школа, 1978. – 224с.
ІНТЕРНЕТ РЕСУРСИ
http:// www.mon.gov.ua.
ДОДАТОК А
1.Достатня умова зростання (спадання) функції на проміжку
Дослідження функції на зростання і спадання спирається на теорему на
достатню умову зростання (спадання) функцій на інтервалі.
Теорема. Якщо f '( x) 0 в кожній точці інтервалу, то функція f на цьому інтервалі зростає; якщо f '( x) 0 у кожній точці інтервалу, то функція f на цьому
інтервалі спадає.
Зауваж ння. Якщо функція f монотонна на інтервалі ]a; b[ і неперервна в точках a і b , то вона монотонна і на відрізку [ a; b] .
Знаходження інтервалів, на яких функція монотонна — інтервалів її монотонності — здійснюється за таким правилом:
- Обчислюють похідну заданої функції, знаходь точки, в яких похідна дорівнює 0 або не існує. Ці точки називаються критичними для функції
- ( x) .
- Критичні точки і точки розриву функції розбивають область її визначення на інтервали, в кожному з яких похідна зберігає знак. Ці інтервали і будуть інтервалами монотонності функції f ( x) .
- Досліджують знак f '( x) на кожному з інтервалів монотонності, визначаючи знак похідної у довільній точці інтервалу (таким він буде на всьому інтервалі). Якщо f '( x) 0 , то функція зростає, якщо f '( x) 0 , то функція спадає.
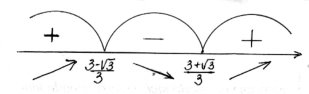
Приклад. Знайти інтервали монотонності функції f ( x ) x 3 3 x 2 2x
Розв’язання
Функція f визначена і диференційована на інтервалі ] ; [ .
![]()
![]()
|
f '( x ) 3x2 6 x 2, знайдемо точки, в яких похідна дорівнює 0. x |
3 |
3 |
|
|
|
|
|
1 |
3 |
|
|
|
|
Так, як f '( x) неперервна функція на R , то вона зберігає знак і на Скористаємось методом інтервалів для визначення знака похідної,
і x2 3 3![]()
![]() 3 .
3 .
![]()
інтервалах.
для цього
|
|
|
|
|
|
28 |
||||
|
|
3 |
|
|
|
|
3 |
|
|
) . Обчисливши |
|
похідну подамо в такому вигляді: f '( x ) 3 ( x |
3 |
) ( x |
3 |
||||||
|
3 |
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
![]()
![]()
значення похідної на інтервалах маємо наступне
|
«Рис. А.1.1» |
|
|
|
|
|
||
|
|
3 |
|
|
|
3 |
|
|
|
Відповідь: Функція зростає на ] ; |
3 |
] |
[ |
3 |
; [ і спадає на проміжку |
||
|
3 |
|
3 |
|
||||
|
|
|
|
|
|
|
||
![]()
![]()
![]()
|
[ |
3 |
3 |
|
; |
3 |
3 |
] . |
|
3 |
|
3 |
|
||||
|
|
|
|
|
|
|
||
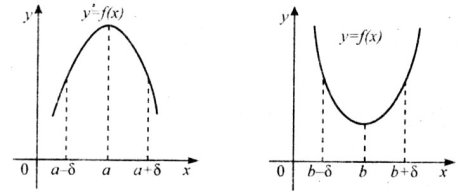
2. Поняття екстремуму функції[8,ст.168]
При дослідженні поведінки функції в деякій точці зручно користуватися поняттям околу. Околом точки а називають будь-який інтервал, що містить цю точку.
Означення. Точка а з області визначення функції f ( x) називається точкою мак имуму цієї функції якщо існує такий окіл точки а, що для всіх x a із цього околу виконується нерівність f ( x ) f ( a) . «рис 3.2.1»
Означення. Точка b із області визначення функції f ( x) називається точкою мінімуму цієї функції, якщо існує такий окіл точки b , що для всіх x b із цього околу виконується нерівність f ( x ) f (b) «рис. 3.2.2»
Точки максимуму і точки мінімуму називають точками к т муму функції,
а значення функції в цих точках — екстремумами функції (максимум і мінімум функції).
«Рис. А.3.1»
29
«Рис. А.2.1» «Рис. А.2.2»
3. Необхідна умова екстремуму
Розглянемо функцію y f ( x) , яка визначена в деякому околі точки x0 , і має
похідну в цій точці.
Теорема Ферма. Якщо х0 — точка екстремуму диференційованої функції
y f ( x) , то f '( x0 ) 0 .
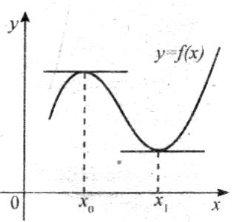
Теорема Ферма має наочний геометричний зміст: у точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт f '( x0 ) 0
«рис. 3.3.1»
Внутрішні точки області визначення функції, у
яких похідна дорівнює нулю, називають стаціонарними. Отже, для того щоб точка х0 була точкою екстремуму, необхідно, щоб вона була стаціонарною.
Сформулюємо достатні умови для того, щоб стаціонарна точка була точкою екстремуму, тобто умови, при виконанні яких стаціонарна точка є точкою максимуму або мінімуму функції.
«Рис. А.3.2»
Якщо похідна ліворуч стаціонарної точки додатна, а праворуч — від'ємна,
тобто при переході через цю точку похідна змінює знак із «+» на «-», то ця стаціонарна точка є точкою максимуму (рис. 3.3.2).
Якщо похідна ліворуч стаціонарної точки від'ємна, а праворуч — додатна,
тобто при переході через стаціонарну точку похідна змінює знак із «-» на «+», то ця стаціонарна точка є точкою мінімуму «рис. 3.3.3».
Якщо при переході через стаціонарну точку похідна не змінює знака, тобто ліворуч і праворуч від стаціонарної точки похідна додатна або від'ємна,
|
то ця точка не є точкою екстремуму. [8,ст.168-169] |
«Рис. А.3.3» |
|
|
Приклад. Дослідити функцію на екстремум
![]()
f ( x ) 3![]() x 2 ( x 5)
x 2 ( x 5)
Розв’язання Знаходимо похідну функції
|
|
2 |
|
|
|
|
|
|
|
2( x 5) 3 x |
|
5 x 2 |
|
|
|||||||||||||||
|
|
|
|
x |
5 3 x2 |
|
|
||||||||||||||||||||||
|
|
f '( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
3 3 |
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|||||||||||
|
|
x |
|
33 x |
|
|
|
x |
|
|
|||||||||||||||||||
|
Знаходимо точки, в яких похідна дорівнює 0, або не існує. В |
|
|
||||||||||||||||||||||||||
|
даному випадку при x 0 похідна має розрив і якщо x 2 , то |
|
|
||||||||||||||||||||||||||
|
перетворюється на 0. Складемо таблицю і побудуємо графік |
|
|
||||||||||||||||||||||||||
|
функції «рис. 3.3.4». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«Рис. А.3.4» |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
] ; 0[ |
|
0 |
|
|
|
|
|
|
]0; 2[ |
|
|
|
2 |
|
|
]2; [ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
f '( x) |
+ |
|
|
|
|
Не існує |
|
|
|
|
- |
|
|
|
|
0 |
|
|
+ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
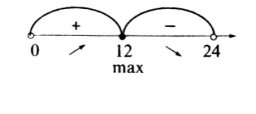
|
f ( x) |
|
|
|
|
|
|
Максимум |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мінімум |
|
|
||||
|
|
|
|
|
|
|
f max f (0) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
f min f (2) 3 3 |
|
4,8 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Відповідь: |
f max f (0) 0 , |
f min f (2) 3 3 |
|
4, 8 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Найбільше і найменше значення функції на проміжку
У практиці часто зустрічаються задачі, у яких треба знайти найбільше або найменше значення функції на замкненому проміжку. Якщо функція монотонна на замкненому проміжку, то найбільшого і найменшого значень вона набуває на його кінцях. Якщо функція не монотонна, але неперервна і має похідну в усіх точках замкненого проміжку, крім можливо, скінченного числа точок, то, щоб відшукати найбільше або найменше її значення потрібно:
- знайти всі критичні точки функції, що належать розглядуваному проміжку, тобто точки, в яких похідна дорівнює 0 або не існує;
- обчислити значення функції в критичних точках і на кінцях проміжку;
- із знайдених чисел вибрати найбільше або найменше.
Отже, неперервна і диференційована функція на заданому відрізку набуває найбільшого і найменшого значень у стаціонарних точках або на кінцях відрізка. [8,ст.170]
Приклад. Знайти найбільше і
|
найменше |
значення |
функції |
||
|
f ( x ) x |
2 |
4 x 3 |
на проміжку [0; 3] |
«Рис. А.4.1» |
|
|
|
|||
Розв’язання
Знаходимо похідну f '( x ) 2 x 4
Знаходимо критичну точку 2 x 4 0 , x 2 . Знайдемо значення функції на кінцях
проміжку [0; 3] : f (0) 3 , f (3) 0 .
Відповідь: Найменше значення функції дорівнює -1 і досягається нею у внутрішній точці проміжку, а найбільше значення 3 і досягається на лівому кінці проміжку (дивись «рис.А.4.1»).
ДОДАТОК Б
ЗАГАЛЬНА СХЕМА ДОСЛІДЖЕННЯ ФУНКЦІЇ.
АЛГОРИТМ ДОСЛІДЖЕННЯ ФУНКЦІЇ
1. Область визначення функції. D(f(x))
|
а) Якщо |
|
|
, то f(x) ≠ 0. |
|
|
|
|
|||
|
б) Якщо |
|
|
|
, то f(x) ≥ 0. |
|
|
|
|
||
|
в) Якщо |
|
|
|
, то f(x)> 0. |
|
г) Якщо |
|
|
|
, то |
д) Якщоy =tg( f ( x ) ), то f(x) ≠ + πn, n Z.
![]()
е) Якщо y = ctg( f ( x ) ), то f(x) ≠πn, n Z.
ж) Якщо y = arcsin( f ( x ) ) або y = arccos( f ( x ) ), то
- Асимптоти
- имптотою називається пряма, до якої графік функції на нескінченності необмежено наближується, але не збігаїться з нею. Або якщо відстань від точки
М(x; f(x)) графіка функції y = f ( x) до прямої наближується до 0, але не дорівнює 0,
то пряма y = kx+l є асимптотою функції.
Асимптоти бувать: вертикальні, похилі горизонтальні.
- Вертикальна асимптота
Якщо або , то x = a –
вертикальна асимптота.
- Похила асимптота має вигляд y = kx + l, де
- b =
- Горизонтальна асимптота. Якщо k=0 і l існує, тоy = l -
![]()
горизонтальна асимптота. Або якщо , то y = l - горизонтальна
асимптота.
3. Точки перетину з осями, проміжки знакосталості
а) Якщо при х=0, f(x) = b, то (0;b)— точки перетину з віссю OY.
|
|
|
|
|
33 |
|
|
б) Якщо при y = 0 |
рівняння має |
корені |
х1, |
x2, то(x; |
0), |
|
(х2; 0).— точки перетину з віссю ОХ. |
|
|
|
|
|
|
в) Нанести точки х1, х2 |
на координату |
пряму |
і |
дослідити |
знак |
|
функції на проміжках. |
|
|
|
|
|
4. Парність
а) Якщо D( f(x)) не є симетричною відносно початку координат, тофункція має загальний вигляд, (ні парна, ні непарна).
б) Якщо D( f ( x) )— симетрична відносно початку координат і виконується умоваf(-x) = f(x), то функція парна.
в) Якщо D( f ( x ) ) — симетрична відносно початку координат і виконується умова f(-x) = - f(x), то функція непарна.
г) ЯкщоD( f ( x) )- симетрична відносно початку координат і не виконуються умови б) і в), то функція має загальний вигляд.
5. Періодичність
Якщо існує таке число Т 0, що f ( x – T ) = f ( x ) = f ( x + T ), то T – період функції.
Щоб знайти період функції, треба розв'язати рівнянняf ( х + Т ) = f(х)
відносно Т для усіхх D(f (x) ).
- Проміжки монотонності та локальні екстремуми
- Знайти f' (x).
- Розв'язати рівняння f' (x) =0 та визначити точки в якихf ' (x ) не існує. (Знайти критичні точки).
а) Якщо критичних точок немає, то дослідити знак f' (x).Якщоf' (x)>0, то функція зростає на всій області визначення. Якщоf' (x)<0, то функція спадає на всій області визначення. Екстремумів немає.
б) Якшо існують критичні точки х1, х2..., то дослідити знакпохідної на проміжках.
Картина дослідження виявилася такою:

На рисунку видні проміжки зростання та спадання й точки в яких функція має мінімум і максимум.
3) Обчислити мінімальні й максимальні значення функції на проміжках minf (x) = f (x1);minf (x) = f (x4); maxf (x) = f (x3)
- Проміжки опуклості, точки перегину
- Знайти f' (x).
- Розв'язати рівнянняf'' (x) = 0та визначити точки, в якихf'' (x) неіснує.
а) Якщо рівняння не має дійсних коренів, то дослідити знак f'' (x) . Якщо f'' (x)
<0, то функція опукла догори. Якщоf'' (x) >0, тофункція опукла донизу на всій області визначення.
б)Якщо рівняння має дійсні корені х1, х2... й точки в яких f'' (x)не існує, то дослідити знак другої похідної на проміжках.
Нехай картина дослідження виявилася такою:

З рисунка видно, що точки дг, і х3 є точками перегину. 3) Обчислити значення функції в точках перегину.
8. Додаткові точки знаходяться в тому разі, коли інформації, отри-
маної в результаті дослідження, буває недостатньо. [10,ст.145-147]


про публікацію авторської розробки
Додати розробку