Опорні схеми (властивості логарифмів, логарифмічна функція, основні типи логарифмічних рівнянь, нерівностей).Умови та розв"язки завдань ЗНО з даної теми.
Про матеріал
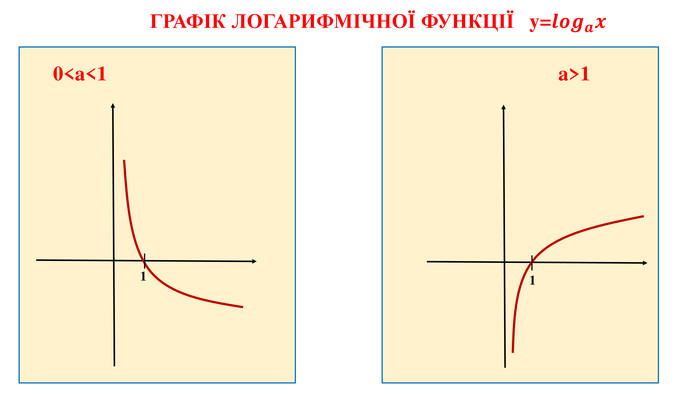
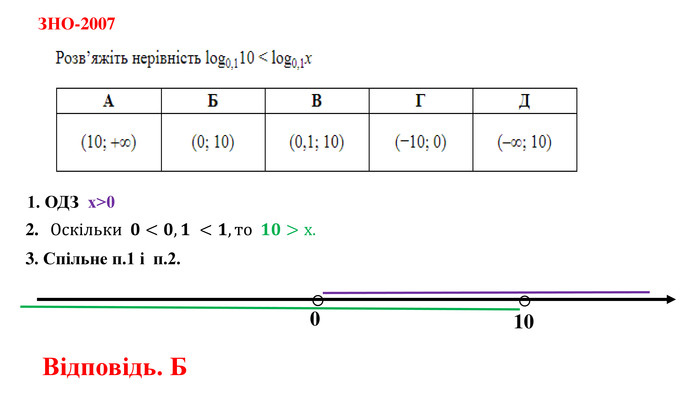
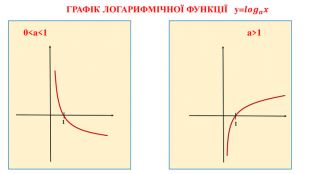
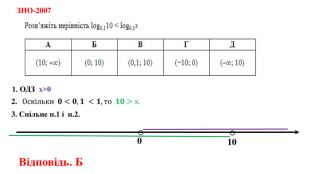
Дані опорні схеми є своєрідною "шпаргалкою" для учнів. Систематизовано і узагальнено навчальний матеріал з теми "Логарифмічна функції". Подані алгоритми розв"язання основних типів логарифмічних рівнянь, нерівностей. Наведено розв"язки характерних завдань з даної теми, які пропонувались випускникам старшої школи під час ЗНО.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






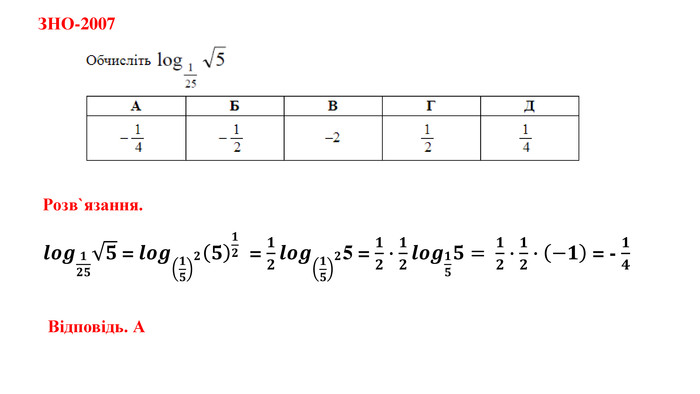








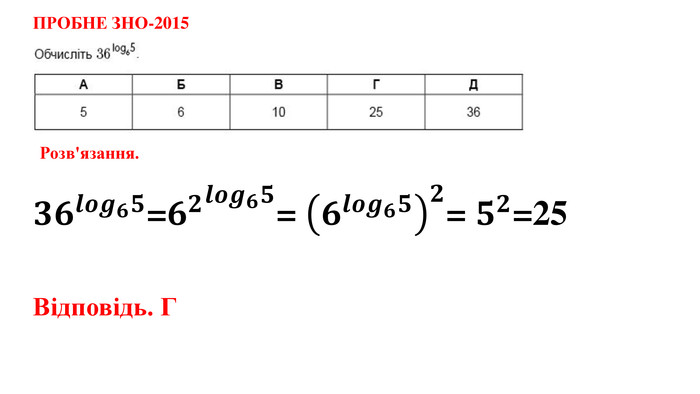

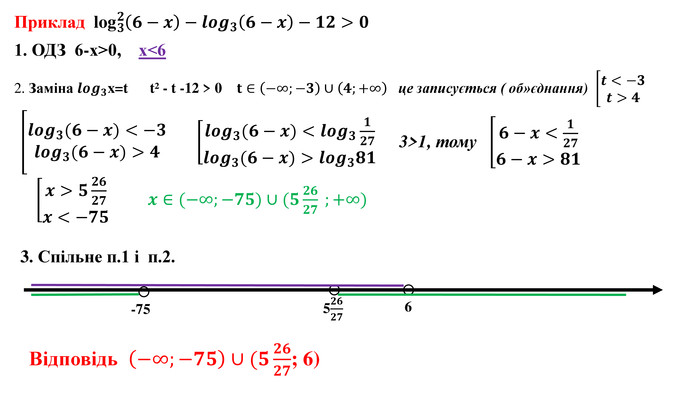












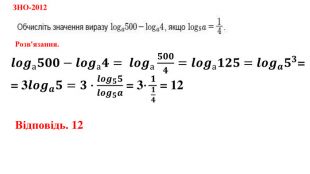



-

Науменко Ірина Анатоліївна
19.09.2024 в 13:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ляшко Олена
22.05.2023 в 13:20
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
01.11.2022 в 19:14
Дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горобець Оксана Михайлівна
30.11.2020 в 12:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук