Урок з алгебри в 11 класі з теми "Застосування похідної"

                                                Урок 11 клас

Тема. Застосування похідної функції. Дослідницька лабораторія.

Мета: розвивати математичну компетентність (розв’язувати задачі  практичного змісту; будувати і досліджувати найпростіші математичні моделі реальних об'єктів, процесів і явищ); формувати інформаційно-цифрову компетентність (структурувати дані; діяти за алгоритмом та складати алгоритми), ініціативність і підприємливість (прогнозувати, ухвалювати оптимальні рішення), соціальну компетентність (висловлювати власну думку, слухати і чути інших, співпрацювати в команді);

             систематизувати і узагальнити знання учнів з теми; познайомити учнів із різними типами прикладних  задач та методами їх розв’язування за допомогою похідної; формувати уміння застосовувати знання та способи дій у нових навчальних ситуаціях; поглибити знання учнів про моделювання процесів дійсності за допомогою похідної функції;

               виховувати культуру праці, зібраність, організованість, увагу, відповідальність та вимогливість до себе; інтерес до математики як засобу пізнання навколишнього світу; сприяти професійному самовизначенню учнів.

Обладнання: комп’ютер, мультимедійний проектор, презентація, роздатковий матеріал.

Тип уроку: комбінований.

Епіграф уроку.                                    

«…немає жодної області в математиці, яка будь-коли не буде застосована до явищ дійсного світу…»

М.І. Лобачевський

Хід уроку

І. Організаційний етап.

Перевірка домашнього завдання.

Які розміри матиме прямокутник найбільшої площі, периметр якого 22 км? (презентація розв’язання задачі - на слайді)

 

ІІ. Мотивація навчальної діяльності.

На попередніх уроках ви засвоїли одне із фундаментальних понять алгебри і початків аналізу – похідну функції. За допомогою похідної ми досліджували і будували графіки функції, знаходили найбільше і найменше значення функції на відрізку, складали рівняння дотичної. І, мабуть, у вас виникало питання: «А навіщо це мені, де я зможе використати вміння знаходження похідної функції?». Наприкінці нашого уроку ви обов’язково отримаєте відповідь на це питання. Отже, починаємо.

Англія, 1666 рік. І.Ньютон, якому лише 23 роки, робить прорив у математиці – відкриває нове поняття похідна елементарної функції. І почалося - життя Європи полетіло так швидко, що вчені не могли навіть уявити такого раніше: розвиток науково-технічного прогресу, виготовлення зброї, епідемії і відкриття цілющого пеніциліну, запуск космічної ракети і створення ядерних реакторів – основою цього всього послужило диференціальне числення. Від високих досягнень до стрімких падінь крокувала поряд похідна, кидаючи свої максимуми і мінімуми¸ похідна, яка миттєво змінила світ.

Подібно тому, як Архімед відкривши закон важеля, сказав: «Дайте мені точку опори і я зрушу Землю», так і сучасники Ньютона казали: «Складіть нам диференціальне рівняння усіх рухів у природі і навчіть їх інтегрувати, тоді ми будемо подібні Богу, оскільки за допомогою обчислень точно будемо знати події майбутнього».

Сьогоднішній урок ми проведемо у дослідницькій лабораторії, в якій з’ясуємо “Як застосовується похідна у різних галузях людського життя». У кожного учня є картка самоконтролю, в якій за участь у кожному етапі уроку виставляє собі оцінку.

ІІІ. «Хай живе теорія» - актуалізація опорних знань

Вправа №1. Щоб ефективно використовувати похідну при розв’язанні конкретних задач, необхідно добре вивчити таблицю похідних елементарних функцій. Наступне завдання дасть змогу перевірити, як ви вмієте обчислювати похідні елементарних та складених функцій. Бажаю всім досягти успіху!

№	Функція	Похідна
1		А)8х7;      Б);     В) 8х8;       Г) інша відповідь
2	(x)=	A) cos 2x ;      Б)2 cos x;      В) -cos2x ;                 Г) інша  відповідь
3	(x)=3x2-5x+6	А)5х-5;      Б) 6х2-5;       В) 6х-5;  Г) інша  відповідь
4	f(x)=ctg x	A);     Б) -;    В); Г) інша   відповідь
5	(x)=x	A) ;    Б) ;    В);   Г) інша відповідь
6	(x)=sin x-cos x	A) –sin x +cos x ;    Б) cos x + sin x ;    В) 0;  Г) інша  відповідь .
7	(x)= (3x+2)50	A) 150(3x+2)49 ;     Б)50(3x+2)49 ;      В)150x;  Г)  інша відповідь
8	(x)=cos3x	A) -3cos x;      Б) -3sin3x;       В)3cosx; Г) інша відповідь

Для самоперевірки - відповіді до вправи пропонуються учням на слайді.

 

 

Вправа №2.

Установіть відповідність між властивостями функцій (1-3) і твердженнями (А-Д).

1. Функція на проміжку спадає.

 

2. Функція на проміжку зростає

 

3. Функція в точці має мінімум

 

 

 

А. Похідна функції в точці дорівнює нулю

Б. Значення функції в точці дорівнює нулю

В. Похідна функції на проміжках від’ємна

Г. Похідна функції на проміжку додатна

Для самоперевірки - відповіді до вправи пропонуються учням на слайді.

Вправа №3. Функція f диференційована і зростає на всій області визначення. Серед наведених графіків укажіть той, який може бути графіком функції y=.

    

 

 

 

 

 

 

 

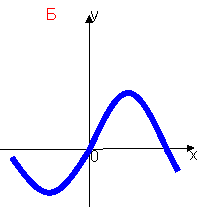
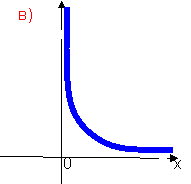
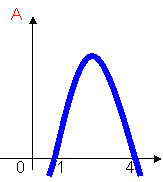
Вправа №4. «Решето»

Завдання. Оберіть послідовність дій для знаходження найбільшого і найменшого значення функції на відрізку. Відсійте зайві твердження. Залатайте дірки у решеті, тобто виправте неточності у твердженнях.

1. Знайти похідну функції y= f(x).
2. Знайти область визначення функції  y= f(x).
3. Упевнитися, що заданий відрізок входить до області визначення даної функції.
4. Побудувати графік даної функції.
5. Знайти критичні точки функції.
6. Знайти проміжки зростання і спадання функції.
7. Обчислити значення функції в критичних точках.
8. Вибрати критичні точки, які належать заданому відрізку.
9. Порівняти одержані значення функції та вибрати з них найменше і найбільше.

(Відповідь: Зайві твердження  4, 6. Правильна послідовність дій 2, 3, 1, 5, 8, 7, 9. Дірка у решеті – неточність у твердженні 7. Обчислити значення функції в критичних точках і на кінцях відрізка.)

III. Узагальнення та систематизація знань, умінь та навичок учнів з теми.

Переходимо до практичних вправ. Уміння працювати самостійно є дуже важливим і в навчанні, і в житті. Але, крім того для досягнення успіху в житті потрібно мати друзів, партнерів. Тому об’єднаємося у 4 групи за рівнем навчальних досягнень. Пропоную для кожної групи завдання (для учнів заготовлені аркуші для подальшої презентації результатів роботи кожної групи біля дошки):

Завдання.

 

1 група (середній рівень). Знайдіть проміжки зростання і спадання функції, точки екстремуму і екстремуми функції y=x³+3x²

2 група (достатній рівень).  Побудуйте графік функції  y=x³-3x²+1

3 група (достатній рівень).  Побудуйте  графік функції y=x⁴-2x²-3

4 група (високий рівень).  Дослідіть функцію і побудуйте її графік  y=

Давайте до кожного графіка доберемо прислів’я:

«Сини і  дочки – з одного дерева листочки» (для парної функції)

«Любиш з гірки котитись, люби й санчата возити»

« Праця чоловіка годує, а лінь марнує»

Фізхвилинка. Очима намалювати побудовані графіки. Рухлива вправа – презентація графіків функції в залежності від знаку похідної.

 

А зараз пропоную розглянути на прикладах, як застосовується похідна в різних галузях науки та життя.

 

Презентація повідомлень учнів-філологів. Послухаємо повідомлення, підготовлені учнями за матеріалами додаткової літератури.

 Виступ учениці, яка підготувала задачу Дідони.

Я хочу звернутись до відомої поеми І.П. Котляревського «Енеїда».

Еней після багатьох пригод пристав до берега і потрапив до міста.

В тім городі жила Дідона,

А город звався Карфаген,

Розумна пані і моторна,

Для неї трохи сих імен:

Трудяща, дуже працьовита,

Весела, гарна, сановита.

 

За легендою, засновниця міста Карфаген Дідона, дочка арійського царя, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод дісталась південного берега Середземного моря. Тут у царя Уарбаса за деяку суму грошей вона купила ділянку землі, «не більшу, ніж можна відміряти шкірою бика». Місцеві жителі неохоче дозволили їй зайняти навіть таку територію і розраховували (розуміючи умову буквально),що Дідоні для нового поселення дістанеться занадто мала ділянка.

Проте, винахідлива Дідона розрізала шкіру бика на тонкі смужки,зв’язала їх у ремінь і, закріпивши один його кінець на березі моря, пішла з другим кінцем у глиб країни. Тоді саме постала перед нею задача: якої форми треба надати ременю, щоб «виміряти шкірою бика» якомога більшу площу. Дідона зіткнулася із цікавою математичною задачею, яку часто називають її іменем.

Оточивши досить величезну територію, Дідона заснувала на ній місто Карфаген. Легенда датує цю подію 825 роком до н.е.

А де ж тут застосування похідної? Погляньте, ще раз на свою домашню задачу… Якщо ця територія - прямокутник, то які його розміри? Відповідь – квадрат.

           Але Дідона була жінкою хитрою. Перед нею постало питання: яку форму потрібно надати мотузці, щоб «обміряти шкурою бика» найбільшу площу?  Цю класичну задачу  Дідона розв’язала правильно. А кривою, що охоплює найбільшу площу, є круг – найдосконаліша, на думку Піфагора, плоска фігура. Дідона охопила на березі моря півкруга для свого міста, де радіус півкруга дорівнював довжині шкіряної мотузки.

 

 

Повернемося до роботи в групах і розподілимо завдання за сферами використання похідної. Кожна група отримує завдання і потім презентує розв’язок, аналізуючи запропоновану задачу.

 

1 група- соціологи (середній рівень). Найкращий вік для самовизначення молоді обчислюється формулою y = -x²+54x+90. У якому віці слід свідомо обирати професію? Чому? (17 років)

 

2 група- маркетологи (достатній рівень). Попит на цукор у місті Бахмут змінюється за законом Р=-x²+16x+30. Знайти максимальний місячний попит серед покупців з 1 (січень) по 10 (жовтень) місяць.

Учитель: Як же можна спрогнозувати попит товару і хто цим займається? Знайомтесь - МАРКЕТОЛОГ (презентація професії)

 

3 група –автоспоживачі (достатній рівень). Витрата пального легкового автомобіля (літр на 100 км) в залежності від швидкості х км/год при русі на четвертій передачі приблизно описується функцією
f(x) = 0,0017 х²-0,18х +10,2. При якій швидкості витрати пального будуть найменшими?

 

4 група- біохіміки (високий рівень). Концентрація ліків у крові хворого через t секунд після ін’єкції задається формулою

С(t)=

Знайти максимальну концентрацію і час, коли вона досягається

 

Для групи учнів-економістів було запропоноване додаткове творче домашнє завдання:

Визначте розміри циліндричної закритої консервної банки, об’єм якої дорівнює V см³, щоб її повна поверхня була найменшою, тобто затрати жерсті на її виготовлення були найменшими.

Учні презентують розв’язання задачі.

Висновок: отже, найменші витрати жерсті на виготовлення консервної банки циліндричної форми будуть за умови, якщо діаметр основи дорівнюватиме висоті банки.

Давайте поміркуємо: Щорічно у нашій країні виготовляють сотні мільйонів банок консервів у жерсті. Але не всі вони мають форму рівностороннього циліндра. Тобто на їх виготовлення передбачається збільшення витрат жерсті. Запитання учням: Як Ви вважаєте, чому виробники несуть такі «нераціональні» на перший погляд витрати? (Бо, наприклад, банка шпротів має діаметр близько 10 см. Тоді і висота банки повинна бути 10 см, але ж - ні.)

За нашими обчисленнями, ціна такої консерви буде у 5 разів більша, бо жерсті необхідно більше для виготовлення саме такої банки. Виробнику вигідно, бо в ціну банки консерви, закладена і ціна жерсті, якої необхідно в 5 разів більше. Тобто споживач переплачує за жерсть, а не за консерви (демонстрація консервних банків).

 

IV. Підсумок уроку. Рефлексія.

Сьогодні на уроці ми побачили багатогранність використання похідної і переконалися, що математика не тільки «цариця», але ще й «служниця» інших наук. Підрахувавши суму балів у «аркуші оцінювання» ви з’ясуєте вашу оцінку за урок.

На «аркушах самооцінювання» є графік функції, що містить проміжки зростання та спадання, точки максимуму та мінімуму. Позначте на точках максимуму, що було максимально зрозумілим, цікавим на уроці; а що викликало труднощі, які зіпсували ваш настрій, - позначте на мінімумі.

Я задоволена вашими знаннями з теми «Застосування похідної», ви вмієте застосовувати набуті знання, а це означає, що кожний з вас, як сьогодні, так і в майбутньому буде компетентний в своїй галузі.

Нехай у вашій формулі успіху будуть зосередженість і працьовитість, взаємодопомога та творчість. Похідною вашого успіху хай стане результат ЗНО, а всі критичні точки нехай будуть тільки точками максимуму.

 

V. Домашнє завдання.  Виконати вправи за підручником Г.П.Бевз

Основний  рівень №810, №808(а)

Достататній рівень №813, №816(а,1)

Високий рівень №826, стор. 214 №10.

Додатки

1група. Знайдіть проміжки зростання і спадання функції, точки екстремуму і екстремуми функції y=x³+3x²

2 група. Побудуйте графік функції  y=x³-3x²+1 за планом: 1)Д(у); 2) похідну 2)критичні точки; 3) проміжки зростання і спадання; 4)точки екстремуму і екстремуми; 5)графік

 3 група. Побудуйте графік функції  y=x⁴-2x²-3 за планом: : 1)Д(у); 2) похідну 2)критичні точки; 3) проміжки зростання і спадання; 4)точки екстремуму і екстремуми; 5)графік

4 група. Дослідіть функцію і побудуйте її графік  y=

 

 

1 група (основний рівень). Найкращий вік для самовизначення молоді обчислюється формулою y = x²-54x+90. У якому віці слід свідомо обирати професію і чому? (17 років)

 2 група (достатній рівень).   Попит на цукор у місті Бахмут змінюється за законом Р=-x²+16x+30. Знайти максимальний місячний попит серед покупців з 1 (січень) по 10 (жовтень) місяць.

3 група (достатній рівень).   Витрата пального легкового автомобіля (літр на 100 км) в залежності від швидкості х км / год при русі на четвертій передачі приблизно описується функцією f (x) = 0,0017 х²-0,18х +10,2. При якій швидкості витрати пального будуть найменшими?
 

4 група. (високий рівень). Концентрація ліків у крові хворого через t секунд після ін’єкції задається формулою

С(t)=

Знайти максимальну концентрацію і час, коли вона досягається

Визначте розміри циліндричної закритої  консервної банки, об’єм  якої дорівнює V см³, щоб її повна поверхня була найменшою, тобто затрати жерсті на її виготовлення були найменшими.

№	Функція	Похідна
1		А) 8х7      Б) ;     В) 8х8       Г) інша відповідь
2	(x)=	A) cos 2x ;      Б)2 cosx;      В)-cos2x ;                 Г) інша  відповідь
3	(x)=3x2-5x+6	А)5х-5;      Б) 6х2-5;       В) 6х-5;  Г) інша  відповідь
4	f(x)=ctg2x	A);     Б)-;    В); Г) інша   відповідь
5	(x)=x	A) ;    Б) ;    В);   Г) інша відповідь
6	(x)=sinx-cosx	A) –sinx +cosx ;    Б) cosx + sinx ;    В)0;  Г) інша  відповідь .
7	(x)= (3x+2)50	A) 150(3x+2)49 ;     Б)50(3x+2)49 ;      В)150x;  Г)  інша відповідь
8	(x)=cos3x	A) -3cos2xsinx;      Б) sin3x;       В)3cosx; Г) інша відповідь

 

№	Функція	Похідна
1		А) 8х7      Б) ;     В) 8х8       Г) інша відповідь
2	(x)=	A) cos 2x ;      Б)2 cosx;      В)-cos2x ;                 Г) інша  відповідь
3	(x)=3x2-5x+6	А)5х-5;      Б) 6х2-5;       В) 6х-5;  Г) інша  відповідь
4	f(x)=ctg2x	A);     Б)-;    В); Г) інша   відповідь
5	(x)=x	A) ;    Б) ;    В);   Г) інша відповідь
6	(x)=sinx-cosx	A) –sinx +cosx ;    Б) cosx + sinx ;    В)0;  Г) інша  відповідь .
7	(x)= (3x+2)50	A) 150(3x+2)49 ;     Б)50(3x+2)49 ;      В)150x;  Г)  інша відповідь
8	(x)=cos3x	A) -3cos2xsinx;      Б) sin3x;       В)3cosx; Г) інша відповідь

 

 

Тест(0,5бза кожне завд.), всього 4 б.	Завдання на відповідність всього 1б.	Решето 0,5 б.за правильну послідовність, 0,5 б.за виправлені неточності	№1(побудова графіків) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-2б	№2(задача) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-3б	Дод. 0,5 бала за графіки	Повідомлення 1б.	Всього
Тест(0,5бза кожне завд.), всього 4 б.	Завдання на відповідність всього 1б.	Решето 0,5 б.за правильну послідовність, 0,5 б.за виправлені неточності	№1(побудова графіків) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-2б	№2(задача)  1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-3б	Дод. 0,5 бала за графіки	Повідомлення 1б.	Всього

 

Тест(0,5бза кожне завд.), всього 4 б.	Завдання на відповідність всього 1б.	Решето 0,5 б.за правильну послідовність, 0,5 б.за виправлені неточності	№1(побудова графіків) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-2б	№2(задача) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-3б	Дод. 0,5 бала за графіки	Повідомлення   1б.	Всього

 

Тест(0,5бза кожне завд.), всього 4 б.	Завдання на відповідність всього 1б.	Решето 0,5 б.за правильну послідовність, 0,5 б.за виправлені неточності	№1(побудова графіків)  1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-2б	№2(задача) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-3б	Дод. 0,5 бала за графіки	Повідомлення 1б.	Всього

 

Тест(0,5бза кожне завд.), всього 4 б.	Завдання на відповідність всього 1б.	Решето 0,5 б.за правильну послідовність, 0,5 б.за виправлені неточності	№1(побудова графіків)  1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-2б	№2(задача) 1гр.-1б. 2гр.-2б. 3гр.-2б. 4гр.-3б	Дод. 0,5 бала за графіки	Повідомлення   1б.	Всього