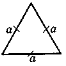Навчальний посібник "Геометричний матеріал"
ВІДДІЛ ОСВІТИ ВИКОНКОМУ ЖОВТОВОДСЬКОЇ МІСЬКОЇ РАДИ
КОМУНАЛЬНИЙ ЗАКЛАД ОСВІТИ ЖОВТОВОДСЬКА СПЕЦІАЛЬНА ЗАГАЛЬНООСВІТНЯ ШКОЛА
ГЕОМЕТРИЧНИЙ
МАТЕРІАЛ
НАВЧАЛЬНИЙ ПОСІБНИК

м. Жовті Води
2018
УКЛАДАЧ:
Лісна Л. М., вчитель математики вищої кваліфікаційної категорії, «учитель-методист» комунального закладу освіти Жовтоводської спеціальної загальноосвітньої школи Дніпропетровської області.
РЕЦЕНЗЕНТИ:
Лукашова Н.Ю., вчитель-дефектолог вищої кваліфікаційної категорії, «учитель-методист», голова методичної ради комунального закладу освіти Жовтоводської спеціальної загалноосвітньої школи Дніпропетровської області.
Стукало У.І., вчитель-дефектолог вищої кваліфікаційної категорії, «учитель-методист», голова методичного об'єднання вчителів-предметників, член методичної ради комунального закладу освіти Жовтоводської спеціальної загальноосвітньої школи Дніпропетровської області.
Лісна Л.М.
Математика. 5-9(10) класи: навчальний посібник «Геометричний матеріал».–Жовті Води, 2018. – 43 с.
Навчальний посібник укладено згідно програми «Математика для 5-9(10) класів спеціальних загальноосвітніх навчальних закладів для дітей з порушенням інтелекту». Посібник написаний спрощеною мовою відповідно до Європейських стандартів подачі інформації, яку легко читати і розуміти. Він стане надійним помічником учням та допоможе корекційним педагогам у доборі матеріалу до уроків.
Розглянуто і схвалено на засіданні
шкільної методичної ради
протокол № 2 від 23.01.2018р.
Голова засідання шкільної методичної
ради
_________________Н.Ю. Лукашова
ПЕРЕДМОВА
Цей навчальний посібник стане в нагоді корекційним педагогам під час підготовки та проведення уроків та допоможе учням краще засвоїти геометричний матеріал.
У навчанні математики геометричний матеріал займає важливе місце та вивчається на окремо виділених для цієї мети уроках.
Наочна геометрія дозволяє формувати у школярів просторові та геометричні уявлення і поняття, креслярські, вимірювальні, графічні навички та вміння.
Посібник містить теоретичний матеріал, завдання практичного характеру для учнів 5-9(10) класів. Така подача матеріалу допоможе прослідкувати поступове ускладненнягеометричного матеріалу від класу до класу і тим самим вірно обрати методи і прийоми вивчення елементів наочної геометрії.
Особлива увага приділяється формуванню навичок роботи з креслярськими інструментами на уроках математики. Наявність геометричних знань сприяєбільш успішному вивченню таких навчальних предметів як трудове навчання, географія, образотворче мистецтво.
В посібнику учні познойомляться з геометричними фігурами
( точка, круг, відрізок, многокутники і т.д.) і геометричними тілами (прямокутний паралелепіпед, куля, циліндр, піраміда, конус), з їх елементарними властивостями, моделюванням, з величинами (довжина, площа, об'єм) та одиницями вимірювання (лінійними, квадратними, кубічними), а також вимірювальними інструментами.
Різноманітні завдання сприятимуть розвитку спостереж-ливості, пам'яті, збагаченню життєвого досвіду учнів, підготовці до трудової діяльності та успішній соціалізації.
Математичні символи та скорочення
|| -паралельність
⊥ - перпендикулярність
 - трикутник
- трикутник
⏋- прямий кут
<А,<1 – позначення кута
r, R – радіус кола, круга
P - периметр
S- площа
V – об'єм
мм - міліметр
см - сантиметр
дм - дециметр
м - метр
мм2, см2, дм2, мм2, км2– квадратні одиниці
мм3 ,см3, дм3, м3, км3 – кубічні одиниці
а - ар
га - гектар
Розділ 1. Точка, пряма, відрізок, промінь.
Точка, пряма, відрізок, промінь – геометричні фігури. Геометричною фігурою також є площина.
Для позначення геометричних фігур використовуються деякі букви латинського алфавіту: А, В (бе), С (це),D(де), Е, М, К, О, Р (пе), R (ер),S (ес),W(ве).
 Відрізок — частина прямої, що складається з усіх точок цієї прямої, котрі лежать між двома даними точками, які називаються кінцями відрізка. Відрізок позначається двома великими латинськими літерами, що відповідають кінцям відрізка.
Відрізок — частина прямої, що складається з усіх точок цієї прямої, котрі лежать між двома даними точками, які називаються кінцями відрізка. Відрізок позначається двома великими латинськими літерами, що відповідають кінцям відрізка.
Кожен відрізок має довжину. Щоб виміряти відрізок лінійкою з поділками, потрібно лівий кінець відрізка сумістити з поділкою лінійки. біля якоїрозміщене число 0, тоді число на лінійці. розміщене біля іншого кінця відрізка, покаже довжину цього відрізка.
Промінь має початок, але не має кінця.
 А
А
Точка А – початок променя.
Запам'ятайте!
Через дві точки проходить тільки одна пряма.
Площина нескінченна, тому її не можна накреслити, але її можна уявити.
1.1 Рівність і нерівність відрізків
Два відрізки вважаються рівними, якщо вони можуть бути суміщені своїми кінцями.
Якщо на даному відрізку взяти дві точки, з яких хоча б одна не збігається з кінцем даного відрізка, то відрізок, обмежений цими точками, називається частиною даного відрізка. Якщо один відрізок дорівнює частині другого, то про ці відрізки кажуть, що перший є меншим, від другого, а другий — більшим від першого.
1.2 Додавання і віднімання відрізків
Додаванням (відніманням) відрізків називається графічна операція, за допомогою якої на деякій прямій можна побудувати відрізок, який є сумою даних відрізків — доданків (або відрізок — різниця відрізків зменшуваного і від'ємника).
Додавання відрізків слід відрізняти від додавання довжин відрізків.
Сумою двох або декількох відрізків називається відрізок, побудований на деякій прямій за даними відрізками без їх взаємного накладання, і без проміжків між ними.
Сума відрізків має переставну і сполучну властивості.
Різницею двох відрізків називається такий третій відрізок, який в сумі з меншим відрізком дорівнює більшому відрізку.
Відрізки можна збільшувати та зменшувати у декілька разів.
Приклад 1.
 Знайти (побудувати) відрізок АВ + MN + EF, де АВ, MN і EF — дані відрізки.
Знайти (побудувати) відрізок АВ + MN + EF, де АВ, MN і EF — дані відрізки.
Розв'язання.
На довільній прямій від довільної точки К відкладаємо в будь-яку сторону один з даних відрізків АВ, MN або EF. Далі на цій же прямій відкладаємо будь-який з відрізків, що залишились, так, щоб один з його кінців сумістився з яким-небудь кінцем відкладеного відрізка, але без накладання цих відрізків. Те ж саме робимо з дальшим відрізком. Отриманий відрізок буде сумою даних відрізків.
Тренувальні вправи
1.Познач дві точки і проведи через них пряму.
2.Познач точку і проведи дві прямі, що проходять через дві точки.
3.Позначпочаток променя і проведи його.
4.Накресли відрізки, довжиною 7 см та 1 см. Знайди їх суму та різницю.
5.Продовж речення:
-дві будь – які точки завжди можна сполучити..........
-дві прямі перетинаються в............
-прямі АВ, СК мають тільки..........спільну точку
-промінь має..........., але не має...........
-через точку О можна провести...........прямих.
6.Відрізок 13см 4мм зменшіть на 2см.
7.Відрізок 3см 5мм збільшіть на 4см 5мм.
8.Відрізок 2см 3мм збільшіть у два рази.
9.Відрізок 9см 6мм зменшіть у три рази.
Розділ 2. Ламана лінія
2.1 Поняття ламаної
Ламана лінія - це геометрична фігура, яка складається з декількох ліній, з'єднаних послідовно своїми кінцями. Кінці кожного відрізка позначаються буквами.

ABCD – це незамкнена ламана лінія. Вона має три ланки: АВ, ВС,CD. Довжина ламаної – це сума довжин ланок ламаної.
Ламана, кінці якої збігаються, називається замкненою.
2.2. Побудова ламаної лінії
Приклад 1. Побудуйте незамкнену ламану лінію ABCD із трьох відрізків довжиною АВ = 4см, ВС = 3см, CD = 5см.
Побудова.
1) Побудуйте відрізок АВ = 4 см.
2) З точки В проведіть в будь – якому напрямі промінь і відкладіть на ньому відрізок ВС = 3 см.
3) З точки С проведіть промінь також у будь – якому напрямі і відкладіть на ньому від точки С відрізок CD = 5 см.
Тренувальні вправи
1.Накресліть незамкнену ламану лінію, позначте її буквами латинського алфавіту. Назвіть відрізки, з яких вона складається.
2.Ламана лінія складається з трьох відрізків завдовжки 4см, 2см, 3см. Накресліть її та обчисліть довжину.
3. Накресліть замкнену ламану лінію з чотирьох відрізків.
4.Накресліть незамкнену ламану лінію МКО, яка складається з відрізків МК = 4см 7мм, КО = 5 см. Обчисліть довжину ламаної лінії МКО.
5. Накресліть дві замкнені ламані лінії, обчисліть довжини цих ламаних . Визначте, довжина якої ламаної лінії більша і на скільки. Відповідь виразіть у міліметрах.
6.Ламана лініяскладається з двох відрізків однакової довжини. Її довжина
- 16м. Чому дорівнює довжина кожного відрізка ламаної ?
7.Серед ламаних, зображених на рисунках, знайдіть замкнену. Назвіть її. Який многокутник вона визначає? Назвіть вершини та сторони цього многокутника.


Розділ 3. Симетрія
Розгляданемо два різні види симетрії: осьову симетрію ( симетрія відносно прямої), центральну симетрію ( симетрія відносно точки).
Цікаво знати !
Важко знайти людину, яка б не мала якогось уявлення про симетрію. «Симетрія» - слово грецького походження ( від грец.- міряти разом). Воно, як і слово «гармонія», означає відповідність, наявність певного порядку.
Витоки поняття симетрії йдуть далеко в минуле до часів Вавілона, Стародавнього Єгипту й Стародавньої Греції. Вже у V-му столітті до н. е. великий філософ і геометр Піфагор вчив: «Число є сутністю усіх речей і організація Всесвіту в її визначеннях являє собою взагалі гармонійну систему чисел та їх відносин». Цим Піфагор хотів підкреслити найважливішу сторону побудови світу — це його впорядкованість, організованість, симетрію, а значить і красу.
3.1 Симетрія відносно точки
Точки X і X1 називаються симетричними відносно точки О, якщо точка О є серединою відрізка XX1

Точка О називається центром симетрії. Точка О є серединою відрізка XX1
Приклад 1. Побудова відрізка та трикутника, симетричних даним, відносно точки .


3.2 Симетрія відносно прямої
Точка  називається симетричною точці X відносно прямої а.
називається симетричною точці X відносно прямої а.

Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно цієї прямої .
На малюнках наведені приклади осей симетрії фігур.


Приклад 2. Побудова трикутника, симетричного даному, відносно прямої.

Відсутність симетрії називають асиметрією.
3.3 Симетрія в природі та архітектурі
Природа дивовижний творець і майстер. Все живе в природі має властивість симетрії.






Тренувальні вправи
- 1.Побудуйте відрізок, симетричний даному відрізку АВ = 3 см відносно осі симетрії.
- 2.Побудуйте відрізок, симетричний даному відрізку АС = 2см 8мм відносно центра симетрії.
- 3.Побудуйте трикутник С1О1К1, симетричний трикутнику СОК відносно осі та центра симетрії.
- 4.Побудуйте квадрат зі стороною 4см, накресліть вісь симетрії і побудуйте квадрат, симетричний першому відносно цієї осі.
Розділ 4. Паралельні та перпендикулярні прямі
4.1 Паралельні прямі
Дві прямі на площині називаються паралельними, якщо вони не перетинаються.
 АВ і СD – паралельні прямі
АВ і СD – паралельні прямі
Записують: AВ || CD. Говорять: “Пряма АВ паралельна прямій CD".
На малюнкуви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.

Подивиться на малюнок . Ви бачите рейки трамвайної колії, які нагадують прямі, що лежать в одній площині і не перетинаються. Це приклад паралельних прямих.
Навколо нас багато інших прикладів паралельних прямих.
Так, у зошиті в клітинку горизонтальні лінії паралельні. Протилежні краї парти, протилежні сторони віконної рами, тролейбусні штанги також паралельні.

Цікаво знати !
Назва “паралельний" походить від грецького слова– “що поряд йде". Символ паралельності || відомий з античних часів. Його використовували Герон і Папп, Олександрійський. Спочатку символ був схожий на нинішній знак рівності, але з появою останнього, щоб уникнути плутанини, символ було повернуто вертикально Вільямом Отредом у 1677 році.
4.2 Перпендикулярніпрямі
Перпендикулярні прямі — прямі, що при перетині утворюють прямий кут; відрізки, що лежать на цих прямих теж називаються перпендикулярними.
Запам'ятайте!
При перетині двох перпендикулярних прямих утворюється чотири прямих кути.
Відрізок, проведений із точки, яка не лежить на прямій, до прямої, називається перпендикуляром, опущеним із точки на пряму..
Коли прямі на площині мають дві спільні точки, то кажуть, що вони збігаються.
На площині дві прямі можуть мати одну спільну точку, тоді вони перетинаються, або не мати жодної спільної точки, тоді вони паралельні.

На малюнкузображено прямі АВ і CD у які перетинаються в точці О під прямим кутом, тобто є перпендикулярними.
Записують: АВ ⊥ CD, а на малюнку ставлять знак прямого кута ⏋.Говорять: “Пряма АВ перпендикулярна до прямої CD".
Для побудови перпендикулярних прямих використовують транспортир або косинець.


АВ і CD – перпендикулярні прямі.
На малюнкуви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.
На малюнкуви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.

Подивиться на перехрестя доріг на малюнку. Вибачите, що дороги нагадують прямі, які перетинаються, утворюючи чотири прямі кути. У цьому випадку говорять, що прямі перетинаються під прямим кутом.
У зошиті з математики клітинки утворюються перпендикулярними прямими.

Цікаво знати !
Назва “перпендикулярний" походить від латинського слова , яке означає “прямовисний". Знак ⊥ запропонував П'єр Ерігон (1530-1643) – французький математик й астроном.
Тренувальні вправи
1. Які прямі називаються перпендикулярними?
2. Як позначають перпендикулярні прямі в записах?
3. Як побудувати пряму, перпендикулярну до даної прямої за допомогою: 1) транспортира і лінійки; 2) косинця?
4. Які прямі називаються паралельними?
5. Як записати, що дані прямі паралельні?
6. Як побудувати пряму, паралельну даній прямій?
7. Чи правий Миколка, коли стверджує, що при перетині двох прямих завжди утворюються рівні кути?
8. За малюнком 1 визначте перпендикулярні прямі: 1) “на око"; 2) за допомогою лінійки і косинця.

Мал. 1
9. За малюнком 2 визначте паралельні прямі: 1) “на око"; 2) за допомогою лінійки і косинця.

Мал. 2
10. На малюнку 3 зображено прямокутник ABCD. Запишіть усі пари перпендикулярних відрізків.

Мал. 3
11. На малюнку 4 зображено квадрат MNPK. Запишіть усі пари перпендикулярних відрізків.
 Мал.4
Мал.4
12. Побудуйте в зошиті пряму АВ (мал. 5). Проведіть за клітинками три прямі, перпендикулярні.
 Мал.5
Мал.5
13.Проведіть пряму CD. За допомогою лінійки і косинця побудуйте пряму MN, паралельну прямій CD.
Розділ 5. Багатокутники ( многокутники)
5.1 Поняттябагатокутника ( многокутника)
Замкнену ламану називають також многокутником (або багатокутником). Її ланки називають сторонами багатокутника, а вершини – вершинами багатокутника.Якщо багатокутник має 3, 4,5, 6 та більше сторін, то його називають відповідно трикутником, чотирикутником, п'ятикутником, шестикутником, n(ен) – кутником. Кожний n– кутник має n вершин і n – сторін.
Сума довжин всіх сторін многокутника називається його периметром.

5.2 Паралелограм,прямокутник, ромб, квадрат та їх властивості
Чотирикутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.

Папалелограм
Прямокутником називають паралелограм, у якого всі кути прямі.
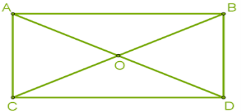
Наприклад: паралелограм ABCD – прямокутник, оскільки  .AD, CB – діагоналі прямокутника.
.AD, CB – діагоналі прямокутника.


Ознаки прямокутника
1.Якщо у паралелограма один із кутів прямий, то цей паралелограм – прямокутник.
2.Якщо у паралелограма діагоналі рівні, то цей паралелограм – прямокутник.
Властивості прямокутника
Прямокутник має всі властивості паралелограма, крім того, діагоналі прямокутника рівні.
Ромбом називається паралелограм, у якого всі сторони рівні.
Наприклад: паралелограм ABCD – ромб, оскільки AB = BC = CD = AD.

 Ромб
Ромб
Ознаки ромба
1.Якщо у паралелограма діагоналі перпендикулярні, то такий паралелограм – ромб.
2.Якщо у чотирикутника сторони рівні, то такий чотирикутник – ромб.
Властивості ромба
Ромб має всі властивості паралелограма, крім того:
1.Діагоналі ромба взаємно перпендикулярні. Наприклад: у ромба ABCD  .
.
2.Діагоналі ромба є бісектрисами його кутів. Наприклад:  і
і  .
.
Квадратом називають прямокутник, у якого всі сторони рівні.
Квадратом називають ромб, у якого всі кути прям
 Квадрат
Квадрат
Властивості квадрата
1.У квадрата всі кути прямі і всі сторони рівні.
2.Діагоналі квадрата рівні і перетинаються під прямим кутом.
3.Діагоналі квадрата є бісектрисами його кутів. Кожна діагональ квадрата утворює зі стороною кут 45°.
5.3 Поняття про трикутник. Периметр трикутника
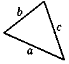
Трикутник – це геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з'єднують ці точки. Точки називають вершинами трикутника, а відрізки – його сторонами.
Наприклад: трикутник із вершинами А, В, С і сторонами АВ, ВС, АС. Цей трикутник позначається так:  .
.


А,В,С – вершини трикутника. АВ, ВС, АС – сторони трикутника
Кути САВ, АВС, АСВ називаються кутами трикутника. Найчастіше їх позначають однією буквою:  . Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
. Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
Периметром трикутника називають суму довжин трьох сторін трикутника.
Якщо периметр трикутника позначити буквою Р, а довжини сторін ВС, АС і АВ – відповідно, через а, b, с, то
Р = а +в +с

Цікаво знати !
А який найвідоміший трикутник ви знаєте? Це звичайно ж Бермудський трикутник! Він отримав таку назву в 50-х роках через географічне розташування точок (вершин трикутника), всередині яких, згідно з існуючою теорією, виникали пов'язані з ним аномалії. Вершинами Бермудського трикутника виступають Бермудські острови, Флорида і Пуерто-Ріко.
5.4 Види трикутників
Розпізнавання трикутників за видами кутів
Залежно від довжини сторін розрізняють різносторонні, рівнобедрені і рівносторонні (або правильні) трикутники.
Трикутник, який має три різні за довжиною сторони, називають різностороннім.

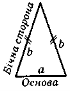
Трикутник, який має дві рівні сторони, називається рівнобедреним. Рівні сторони називаються бічними, а третя сторона – основою трикутника.
Наприклад:  – рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.
– рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.

Трикутник, у якого всі сторони рівні, називають рівностороннім, або правильним.
У рівностороннього трикутника всі кути рівні, величина кожного з них дорівнює 60°.

Розпізнавання трикутників за кутами
Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
Гострокутним називається трикутник, у якого всі кути гострі.

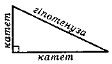
Прямокутним називається трикутник, у якого є прямий кут. Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а дві інші сторони – катетами.
Наприклад: сторона АС – гіпотенуза, сторони АВ і ВС – катети.

Тупокутним називається трикутник, у якого є тупий кут.

Висотою трикутника називають перпендикуляр, проведений із його вершини до прямої, яка має протилежну сторону.
Наприклад: відрізок BD – висота відповідно гострокутного, тупокутного і прямокутного трикутників.



Запам'ятайте!
Види трикутників
| За довжинами сторін: | За величиною найбільшого кута: |
|
|
|
|
|
|
|
|
|
5.5 Побудова трикутників
Трикутник можна побудувати, якщо відома довжина кожної його сторони. Для побудови трикутника потрібні циркуль, лінійка і олівець.
Приклад 1. Треба побудувати різносторонній трикутник ВАС з довжиною сторін: ВС = 6 см, СА = 4 см, ВА = 2 см .
Будувати треба так.
1. Провести пряму.
2. На прямій від обраної точки В відкласти відрізок , що дорівнює даному відрізку a (ВС)= 6 см, і зазначити інший кінець відрізка С.
3. Провести коло з центром С і радіусом, що дорівнює відрізку b(СА) = 4 см.
4. Провести коло з центром В і радіусом, що дорівнює відрізку c(ВА)= 2 см.
5. Точка перетину кіл є третьою вершиною А шуканого трикутника.
6. Сполучіть точки В, А, С. Назвіть знайдений трикутник. Виміряйте його сторони. Назвіть вид трикутника ВАС.

5.6 Шестикутник. Побудова правильного шестикутника
Шестикутник ( гексагон) — многокутник, що має шість вершин та шість сторін.
Шестикутник, у якого всі сторони рівні, називається правильним.


Побудова правильного шестикутника
1. Будуємо коло вибраного радіуса та проводимо його діаметр.
2.З протилежних кінців одного з діаметрів кола (наприклад, т. 1і 4)
описують дуги циркулем, розхил якого рівний радіусу кола.
3. Точки перетину цих дуг з колом, точки 2, 3, 5,6 разом з точками 1 і 4 ділять коло на 6 рівних частин.
4.З'єднавши точки 1,2,3,4,5,6 дістанемо правильний шестикутник.
Правильний шестикутник у природі, техніці та культурі.
Цікаво знати ! 

- Ø Бджолині стільники наочно показують розбиття площини на правильні шестикутники.
- Ø Деякі складні молекули вуглецю (наприклад, графіт) мають гексагональну кристалічну ґратку.
- Ø Гігантський гексагон — атмосферне явище на Сатурні.
- Ø Перетин гайки, багатьох олівців має вигляд правильного шестикутника.
- Ø Гексаграма — шестикутна зірка, утворена двома рівносторонніми трикутниками, є, зокрема, символом юдаїзму.
- Ø Контур Франції нагадує правильний шестикутник, тому ця фігура — символ країни. Вислів «гексагон» у французькій мові широко вживається як перифраз назви «Франція». Форма шестикутника використовується також на французьких монетах євро. Щоправда, порівняння Франції з шестикутником відносно
- недавнє.
Тренувальні вправи
1. Які багатокутники ви бачите на рисунку?








- 2.Спираючись на рисунок, назвіть усі вершини, усі сторони та всі кути чотирикутника MNPK. Визначте на око, чи є у цьому чотирикутнику прямий, тупий, гострий кути. Скільки яких кутів?
3.Знайдіть периметри трикутників, зображенихна рисунках (довжини сторін зазначено у метрах).

4.Накресліть чотирикутник з двома прямими кутами. Які у нього два інших кути?


5.Накресліть: 1) чотирикутник; 2) п'ятикутник; 3) шестикутник;
4) семикутник.
6.Знайдіть периметр прямокутника, як що його сторони дорівнюють 3 см,
- 4см .
7.Скільки сторін, вершин, кутів у трикутника; чотирикутника; шестикутника ?
8.Серед чотирикутників, зображених на рисунках, знайдіть прямокутники.






9.Скільки прямокутників на рисунках?


10.Якої довжини треба взяти кусок дротини, щоб зробити з нього:
а) квадрат зі стороною 3 см?
б) прямокутник зі сторонами 15 см і 4 см?
11. Побудуйте та зафарбуйте різними кольорами:
а) прямокутник зі сторонами 3 см і 5 см;
б) квадрат зі стороною 4 см.
12.Периметр квадрата 36 м. Яка його сторона?
13.Периметр прямокутника 36 см, довжина — 11 см. Знайдіть ширину пря- мокутника.
14. Заповніть таблицю для прямокутників.
| а | 23 см | 125 м | |
| b | 17 см | | 1250 км |
| Р | | 1000 м |
|
15.Яка площа квадрата зі стороною 9 см?
16.Яка площа прямокутника зі сторонами 5 см і 3 см?
17.10 га = ? а.
18.Периметр квадрата 20 см. Знайдіть його площу.
19.Площа прямокутника 126 см2, його довжина — 21 см. Знайдіть ширину прямокутника.
20.На рисунку зображений рівнобедрений трикутник ABC. Назвіть:
 а)основу;
а)основу;
б) бічні сторони;
21.Визначте вид трикутника за його кутами:
а) 34°, 127°, 19°;в) 45°, 60°, 75°;
б) 40°, 50°, 90°;г) 95°, 85°, 5°.
22. Накресліть рівносторонній, різносторонній та рівнобедрений трикутники, позначте їх. Виміряйте сторони кожного трикутника.
23. Побудувати різносторонній трикутник ВАС з довжиною сторін: ВС = 3 см 6мм, СА = 4 см, ВА = 2 см . При допомозі лінійки виміряйте правильність побудови.
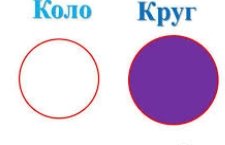
Розділ 6. Коло. Круг
6.1 Коло
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки — центра кола.


Мал. 1. Коло
Радіус кола — відстань від точок кола до його центра. Радіус кола зазвичай позначається буквами r, R.
Хорда — відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Діаметр зазвичай позначають буквами d,D.
Дотична — пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. Через будь-яку точку, що лежить поза колом і належить площині кола, можна провести дві різні дотичні.
Запам'ятайте!
Діаметр у два рази більший за радіус.
6.2 Круг
Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка — центр круга. Радіус — задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.
Запам'ятайте!
Коло – це замкнена крива лінія. Вона має довжину.
Круг – плоска фігура, що має площу.


Сектором називається частина круга, що обмежена двома його радіусами.
Сегментом називається частина круга, що обмежена хордою і дугою.
Тренувальні вправи
1.Яку геометричну фігуру називають колом, кругом ?
2.Скільки в колі можна провести радіусів, діаметрів ?
3.Чи можна діаметр назвати хордою ?
4.У скільки разів діаметр більший за радіус ?
5. Накресліть кола радіусом 2см, 4 см. чому дорівнюють їх діаметри ?
6. Накресліть кола радіусами 3см 5мм, 4см 2мм, 5см. Яке з цих кіл буде найбільшим, найменшим ?
7.На колі лежать точки А, В, С. Чи на однаковій відстані вони від центра кола О ?
8.Накреслити круг довільного радіусу. Позначити в ньому сектор, сегмент.
ВІДДІЛ ОСВІТИ ВИКОНКОМУ ЖОВТОВОДСЬКОЇ МІСЬКОЇ РАДИ
КОМУНАЛЬНИЙ ЗАКЛАД ОСВІТИ ЖОВТОВОДСЬКА СПЕЦІАЛЬНА ЗАГАЛЬНООСВІТНЯ ШКОЛА

ГЕОМЕТРИЧНИЙ
МАТЕРІАЛ
НАВЧАЛЬНИЙ ПОСІБНИК

м. Жовті Води
2018
УКЛАДАЧ:
Лісна Л. М., вчитель математики вищої кваліфікаційної категорії, «учитель-методист» комунального закладу освіти Жовтоводської спеціальної загальноосвітньої школи Дніпропетровської області.
РЕЦЕНЗЕНТИ:
Лукашова Н.Ю., вчитель-дефектолог вищої кваліфікаційної категорії, «учитель-методист», голова методичної ради комунального закладу освіти Жовтоводської спеціальної загалноосвітньої школи Дніпропетровської області.
Стукало У.І., вчитель-дефектолог вищої кваліфікаційної категорії, «учитель-методист», голова методичного об’єднання вчителів-предметників, член методичної ради комунального закладу освіти Жовтоводської спеціальної загальноосвітньої школи Дніпропетровської області.
Лісна Л.М.
Математика. 5-9(10) класи: навчальний посібник «Геометричний матеріал». –Жовті Води, 2018. – 43 с.
Навчальний посібник укладено згідно програми «Математика для 5-9(10) класів спеціальних загальноосвітніх навчальних закладів для дітей з порушенням інтелекту». Посібник написаний спрощеною мовою відповідно до Європейських стандартів подачі інформації, яку легко читати і розуміти. Він стане надійним помічником учням та допоможе корекційним педагогам у доборі матеріалу до уроків.
Розглянуто і схвалено на засіданні
шкільної методичної ради
протокол № 2 від 23.01.2018р.
Голова засідання шкільної методичної
ради
_________________Н.Ю. Лукашова
ПЕРЕДМОВА
Цей навчальний посібник стане в нагоді корекційним педагогам під час підготовки та проведення уроків та допоможе учням краще засвоїти геометричний матеріал.
У навчанні математики геометричний матеріал займає важливе місце та вивчається на окремо виділених для цієї мети уроках.
Наочна геометрія дозволяє формувати у школярів просторові та геометричні уявлення і поняття, креслярські, вимірювальні, графічні навички та вміння.
Посібник містить теоретичний матеріал, завдання практичного характеру для учнів 5-9(10) класів. Така подача матеріалу допоможе прослідкувати поступове ускладнення геометричного матеріалу від класу до класу і тим самим вірно обрати методи і прийоми вивчення елементів наочної геометрії.
Особлива увага приділяється формуванню навичок роботи з креслярськими інструментами на уроках математики. Наявність геометричних знань сприяє більш успішному вивченню таких навчальних предметів як трудове навчання, географія, образотворче мистецтво.
В посібнику учні познойомляться з геометричними фігурами
( точка, круг, відрізок, многокутники і т.д.) і геометричними тілами (прямокутний паралелепіпед, куля, циліндр, піраміда, конус), з їх елементарними властивостями, моделюванням, з величинами (довжина, площа, об’єм) та одиницями вимірювання (лінійними, квадратними, кубічними), а також вимірювальними інструментами.
Різноманітні завдання сприятимуть розвитку спостереж-ливості, пам’яті, збагаченню життєвого досвіду учнів, підготовці до трудової діяльності та успішній соціалізації.
Математичні символи та скорочення
|| - паралельність
⊥ - перпендикулярність
![]() - трикутник
- трикутник
⏋- прямий кут
<А, <1 – позначення кута
r, R – радіус кола, круга
P - периметр
S- площа
V – об’єм
мм - міліметр
см - сантиметр
дм - дециметр
м - метр
мм2, см2, дм2, мм2, км2– квадратні одиниці
мм3 ,см3, дм3, м3, км3 – кубічні одиниці
а - ар
га - гектар
Розділ 1. Точка, пряма, відрізок, промінь.
Точка, пряма, відрізок, промінь – геометричні фігури. Геометричною фігурою також є площина.
Для позначення геометричних фігур використовуються деякі букви латинського алфавіту: А, В (бе), С (це), D(де), Е, М, К, О, Р (пе), R (ер), S (ес), W(ве).
 Відрізок — частина прямої, що складається з усіх точок цієї прямої, котрі лежать між двома даними точками, які називаються кінцями відрізка. Відрізок позначається двома великими латинськими літерами, що відповідають кінцям відрізка.
Відрізок — частина прямої, що складається з усіх точок цієї прямої, котрі лежать між двома даними точками, які називаються кінцями відрізка. Відрізок позначається двома великими латинськими літерами, що відповідають кінцям відрізка.
Кожен відрізок має довжину. Щоб виміряти відрізок лінійкою з поділками, потрібно лівий кінець відрізка сумістити з поділкою лінійки. біля якоїрозміщене число 0, тоді число на лінійці. розміщене біля іншого кінця відрізка, покаже довжину цього відрізка.
Промінь має початок, але не має кінця.
 А
А
Точка А – початок променя.
Запам’ятайте!
Через дві точки проходить тільки одна пряма.
Площина нескінченна, тому її не можна накреслити, але її можна уявити.
1.1 Рівність і нерівність відрізків
Два відрізки вважаються рівними, якщо вони можуть бути суміщені своїми кінцями.
Якщо на даному відрізку взяти дві точки, з яких хоча б одна не збігається з кінцем даного відрізка, то відрізок, обмежений цими точками, називається частиною даного відрізка. Якщо один відрізок дорівнює частині другого, то про ці відрізки кажуть, що перший є меншим, від другого, а другий — більшим від першого.
1.2 Додавання і віднімання відрізків
Додаванням (відніманням) відрізків називається графічна операція, за допомогою якої на деякій прямій можна побудувати відрізок, який є сумою даних відрізків — доданків (або відрізок — різниця відрізків зменшуваного і від’ємника).
Додавання відрізків слід відрізняти від додавання довжин відрізків.
Сумою двох або декількох відрізків називається відрізок, побудований на деякій прямій за даними відрізками без їх взаємного накладання, і без проміжків між ними.
Сума відрізків має переставну і сполучну властивості.
Різницею двох відрізків називається такий третій відрізок, який в сумі з меншим відрізком дорівнює більшому відрізку.
Відрізки можна збільшувати та зменшувати у декілька разів.
Приклад 1.
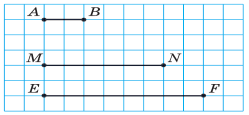 Знайти (побудувати) відрізок АВ + MN + EF, де АВ, MN і EF — дані відрізки.
Знайти (побудувати) відрізок АВ + MN + EF, де АВ, MN і EF — дані відрізки.
Розв’язання.
На довільній прямій від довільної точки К відкладаємо в будь-яку сторону один з даних відрізків АВ, MN або EF. Далі на цій же прямій відкладаємо будь-який з відрізків, що залишились, так, щоб один з його кінців сумістився з яким-небудь кінцем відкладеного відрізка, але без накладання цих відрізків. Те ж саме робимо з дальшим відрізком. Отриманий відрізок буде сумою даних відрізків.
Тренувальні вправи
- Познач дві точки і проведи через них пряму.
- Познач точку і проведи дві прямі, що проходять через дві точки.
- Познач початок променя і проведи його.
- Накресли відрізки, довжиною 7 см та 1 см. Знайди їх суму та різницю.
- Продовж речення:
- дві будь – які точки завжди можна сполучити..........
- дві прямі перетинаються в............
- прямі АВ, СК мають тільки..........спільну точку
- промінь має..........., але не має...........
- через точку О можна провести...........прямих.
- Відрізок 13см 4мм зменшіть на 2см.
7.Відрізок 3см 5мм збільшіть на 4см 5мм.
8.Відрізок 2см 3мм збільшіть у два рази.
9.Відрізок 9см 6мм зменшіть у три рази.
Розділ 2. Ламана лінія
2.1 Поняття ламаної
Ламана лінія - це геометрична фігура, яка складається з декількох ліній, з’єднаних послідовно своїми кінцями. Кінці кожного відрізка позначаються буквами.
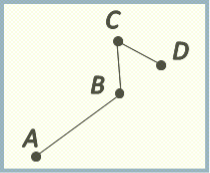
ABCD – це незамкнена ламана лінія. Вона має три ланки: АВ, ВС,CD. Довжина ламаної – це сума довжин ланок ламаної.
Ламана, кінці якої збігаються, називається замкненою.
2.2. Побудова ламаної лінії
Приклад 1. Побудуйте незамкнену ламану лінію ABCD із трьох відрізків довжиною АВ = 4см, ВС = 3см, CD = 5см.
Побудова.
1) Побудуйте відрізок АВ = 4 см.
2) З точки В проведіть в будь – якому напрямі промінь і відкладіть на ньому відрізок ВС = 3 см.
3) З точки С проведіть промінь також у будь – якому напрямі і відкладіть на ньому від точки С відрізок CD = 5 см.
Тренувальні вправи
1.Накресліть незамкнену ламану лінію, позначте її буквами латинського алфавіту. Назвіть відрізки, з яких вона складається.
2.Ламана лінія складається з трьох відрізків завдовжки 4см, 2см, 3см. Накресліть її та обчисліть довжину.
3. Накресліть замкнену ламану лінію з чотирьох відрізків.
4.Накресліть незамкнену ламану лінію МКО, яка складається з відрізків МК = 4см 7мм, КО = 5 см. Обчисліть довжину ламаної лінії МКО.
5. Накресліть дві замкнені ламані лінії, обчисліть довжини цих ламаних . Визначте, довжина якої ламаної лінії більша і на скільки. Відповідь виразіть у міліметрах.
6.Ламана лініяскладається з двох відрізків однакової довжини. Її довжина
- м. Чому дорівнює довжина кожного відрізка ламаної ?
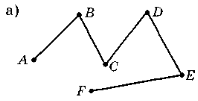
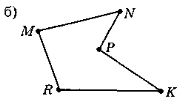
7.Серед ламаних, зображених на рисунках, знайдіть замкнену. Назвіть її. Який многокутник вона визначає? Назвіть вершини та сторони цього многокутника.
Розділ 3. Симетрія
Розгляданемо два різні види симетрії: осьову симетрію ( симетрія відносно прямої), центральну симетрію ( симетрія відносно точки).
Цікаво знати !
Важко знайти людину, яка б не мала якогось уявлення про симетрію. «Симетрія» - слово грецького походження ( від грец.- міряти разом). Воно, як і слово «гармонія», означає відповідність, наявність певного порядку.
Витоки поняття симетрії йдуть далеко в минуле до часів Вавілона, Стародавнього Єгипту й Стародавньої Греції. Вже у V-му столітті до н. е. великий філософ і геометр Піфагор вчив: «Число є сутністю усіх речей і організація Всесвіту в її визначеннях являє собою взагалі гармонійну систему чисел та їх відносин». Цим Піфагор хотів підкреслити найважливішу сторону побудови світу — це його впорядкованість, організованість, симетрію, а значить і красу.
3.1 Симетрія відносно точки
Точки X і X1 називаються симетричними відносно точки О, якщо точка О є серединою відрізка XX1
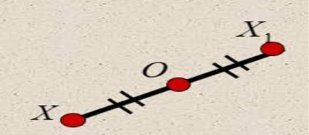
Точка О називається центром симетрії. Точка О є серединою відрізка XX1
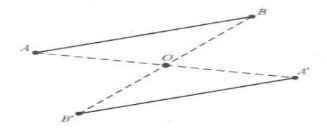
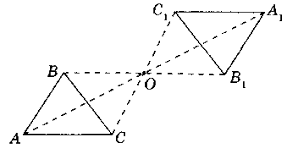
Приклад 1. Побудова відрізка та трикутника, симетричних даним, відносно точки .
3.2 Симетрія відносно прямої
Точка ![]() називається симетричною точці X відносно прямої а.
називається симетричною точці X відносно прямої а.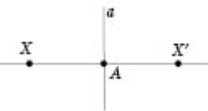
Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно цієї прямої .
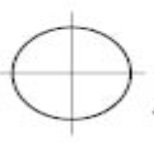
На малюнках наведені приклади осей симетрії фігур.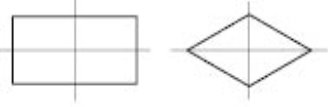
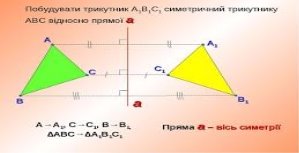
Приклад 2. Побудова трикутника, симетричного даному, відносно прямої.
Відсутність симетрії називають асиметрією.
3.3 Симетрія в природі та архітектурі
Природа дивовижний творець і майстер. Все живе в природі має властивість симетрії.






Тренувальні вправи
- Побудуйте відрізок, симетричний даному відрізку АВ = 3 см відносно осі симетрії.
- Побудуйте відрізок, симетричний даному відрізку АС = 2см 8мм відносно центра симетрії.
- Побудуйте трикутник С1О1К1, симетричний трикутнику СОК відносно осі та центра симетрії.
- Побудуйте квадрат зі стороною 4см, накресліть вісь симетрії і побудуйте квадрат, симетричний першому відносно цієї осі.
Розділ 4. Паралельні та перпендикулярні прямі
4.1 Паралельні прямі
Дві прямі на площині називаються паралельними, якщо вони не перетинаються.
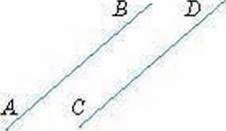 АВ і СD – паралельні прямі
АВ і СD – паралельні прямі
Записують: AВ || CD. Говорять: “Пряма АВ паралельна прямій CD”.
На малюнку ви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.
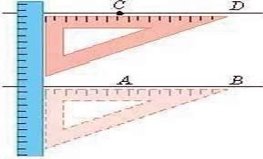
Подивиться на малюнок . Ви бачите рейки трамвайної колії, які нагадують прямі, що лежать в одній площині і не перетинаються. Це приклад паралельних прямих.
Навколо нас багато інших прикладів паралельних прямих.
Так, у зошиті в клітинку горизонтальні лінії паралельні. Протилежні краї парти, протилежні сторони віконної рами, тролейбусні штанги також паралельні.

Цікаво знати !
Назва “паралельний” походить від грецького слова – “що поряд йде”. Символ паралельності || відомий з античних часів. Його використовували Герон і Папп, Олександрійський. Спочатку символ був схожий на нинішній знак рівності, але з появою останнього, щоб уникнути плутанини, символ було повернуто вертикально Вільямом Отредом у 1677 році.
4.2 Перпендикулярні прямі
Перпендикулярні прямі — прямі, що при перетині утворюють прямий кут; відрізки, що лежать на цих прямих теж називаються перпендикулярними.
Запам’ятайте!
При перетині двох перпендикулярних прямих утворюється чотири прямих кути.
Відрізок, проведений із точки, яка не лежить на прямій, до прямої, називається перпендикуляром, опущеним із точки на пряму..
Коли прямі на площині мають дві спільні точки, то кажуть, що вони збігаються.
На площині дві прямі можуть мати одну спільну точку, тоді вони перетинаються, або не мати жодної спільної точки, тоді вони паралельні.
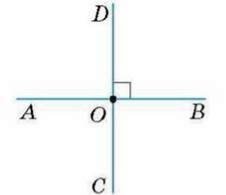
На малюнку зображено прямі АВ і CD у які перетинаються в точці О під прямим кутом, тобто є перпендикулярними.
Записують: АВ ⊥ CD, а на малюнку ставлять знак прямого кута ⏋.Говорять: “Пряма АВ перпендикулярна до прямої CD”.
Для побудови перпендикулярних прямих використовують транспортир або косинець.
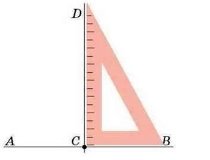
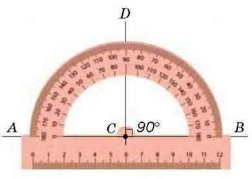
АВ і CD – перпендикулярні прямі.
На малюнку ви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.
На малюнку ви бачите, як за допомогою лінійки і косинця через точку С провели пряму CD, паралельну прямій AВ.
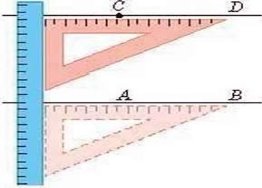
Подивиться на перехрестя доріг на малюнку. Вибачите, що дороги нагадують прямі, які перетинаються, утворюючи чотири прямі кути. У цьому випадку говорять, що прямі перетинаються під прямим кутом.
У зошиті з математики клітинки утворюються перпендикулярними прямими.

Цікаво знати !
Назва “перпендикулярний” походить від латинського слова , яке означає “прямовисний”. Знак ⊥ запропонував П’єр Ерігон (1530-1643) – французький математик й астроном.
Тренувальні вправи
1. Які прямі називаються перпендикулярними?
2. Як позначають перпендикулярні прямі в записах?
3. Як побудувати пряму, перпендикулярну до даної прямої за допомогою: 1) транспортира і лінійки; 2) косинця?
4. Які прямі називаються паралельними?
5. Як записати, що дані прямі паралельні?
6. Як побудувати пряму, паралельну даній прямій?
7. Чи правий Миколка, коли стверджує, що при перетині двох прямих завжди утворюються рівні кути?
8. За малюнком 1 визначте перпендикулярні прямі: 1) “на око”; 2) за допомогою лінійки і косинця.
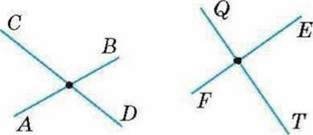
Мал. 1
9. За малюнком 2 визначте паралельні прямі: 1) “на око”; 2) за допомогою лінійки і косинця.
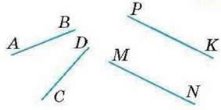
Мал. 2
10. На малюнку 3 зображено прямокутник ABCD. Запишіть усі пари перпендикулярних відрізків.

Мал. 3
11. На малюнку 4 зображено квадрат MNPK. Запишіть усі пари перпендикулярних відрізків.
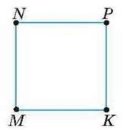 Мал.4
Мал.4
12. Побудуйте в зошиті пряму АВ (мал. 5). Проведіть за клітинками три прямі, перпендикулярні.
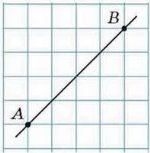 Мал.5
Мал.5
13.Проведіть пряму CD. За допомогою лінійки і косинця побудуйте пряму MN, паралельну прямій CD.
Розділ 5. Багатокутники ( многокутники)
5.1 Поняття багатокутника ( многокутника)
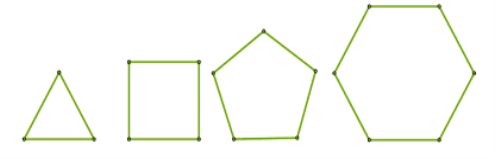
Замкнену ламану називають також многокутником (або багатокутником). Її ланки називають сторонами багатокутника, а вершини – вершинами багатокутника.Якщо багатокутник має 3, 4,5, 6 та більше сторін, то його називають відповідно трикутником, чотирикутником, п’ятикутником, шестикутником, n(ен) – кутником. Кожний n– кутник має n вершин і n – сторін.
Сума довжин всіх сторін многокутника називається його периметром.
5.2 Паралелограм, прямокутник, ромб, квадрат та їх властивості
Чотирикутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.

Папалелограм
Прямокутником називають паралелограм, у якого всі кути прямі.
Наприклад: паралелограм ABCD – прямокутник, оскільки ![]() .AD, CB – діагоналі прямокутника.
.AD, CB – діагоналі прямокутника.

Ознаки прямокутника
- Якщо у паралелограма один із кутів прямий, то цей паралелограм – прямокутник.
- Якщо у паралелограма діагоналі рівні, то цей паралелограм – прямокутник.
Властивості прямокутника
Прямокутник має всі властивості паралелограма, крім того, діагоналі прямокутника рівні.
Ромбом називається паралелограм, у якого всі сторони рівні.
Наприклад: паралелограм ABCD – ромб, оскільки AB = BC = CD = AD.
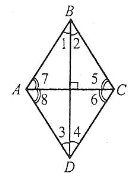
 Ромб
Ромб
Ознаки ромба
- Якщо у паралелограма діагоналі перпендикулярні, то такий паралелограм – ромб.
- Якщо у чотирикутника сторони рівні, то такий чотирикутник – ромб.
Властивості ромба
Ромб має всі властивості паралелограма, крім того:
-
Діагоналі ромба взаємно перпендикулярні. Наприклад: у ромба ABCD
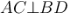 .
.
-
Діагоналі ромба є бісектрисами його кутів. Наприклад:
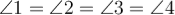 і
і 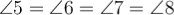 .
.
Квадратом називають прямокутник, у якого всі сторони рівні.
Квадратом називають ромб, у якого всі кути прям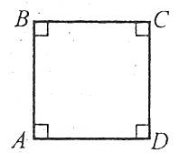
 Квадрат
Квадрат
Властивості квадрата
- У квадрата всі кути прямі і всі сторони рівні.
- Діагоналі квадрата рівні і перетинаються під прямим кутом.
-
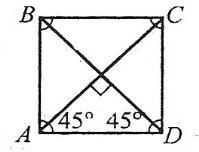
Діагоналі квадрата є бісектрисами його кутів. Кожна діагональ квадрата утворює зі стороною кут 45°.
5.3 Поняття про трикутник. Периметр трикутника
Трикутник – це геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з’єднують ці точки. Точки називають вершинами трикутника, а відрізки – його сторонами.
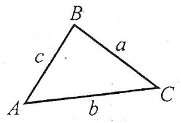
Наприклад: трикутник із вершинами А, В, С і сторонами АВ, ВС, АС. Цей трикутник позначається так: ![]() .
.
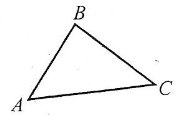
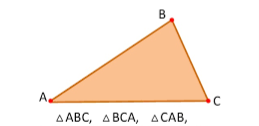
А,В,С – вершини трикутника. АВ, ВС, АС – сторони трикутника
Кути САВ, АВС, АСВ називаються кутами трикутника. Найчастіше їх позначають однією буквою: ![]() . Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
. Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
Периметром трикутника називають суму довжин трьох сторін трикутника.
Якщо периметр трикутника позначити буквою Р, а довжини сторін ВС, АС і АВ – відповідно, через а, b, с, то
Р = а +в +с
Цікаво знати !
А який найвідоміший трикутник ви знаєте? Це звичайно ж Бермудський трикутник! Він отримав таку назву в 50-х роках через географічне розташування точок (вершин трикутника), всередині яких, згідно з існуючою теорією, виникали пов’язані з ним аномалії. Вершинами Бермудського трикутника виступають Бермудські острови, Флорида і Пуерто-Ріко.
5.4 Види трикутників
Розпізнавання трикутників за видами кутів
Залежно від довжини сторін розрізняють різносторонні, рівнобедрені і рівносторонні (або правильні) трикутники.
Трикутник, який має три різні за довжиною сторони, називають різностороннім.
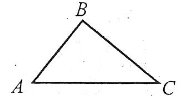
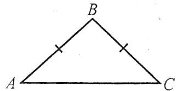
Трикутник, який має дві рівні сторони, називається рівнобедреним. Рівні сторони називаються бічними, а третя сторона – основою трикутника.
Наприклад: ![]() – рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.
– рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.
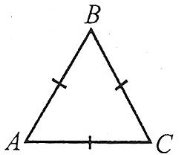
Трикутник, у якого всі сторони рівні, називають рівностороннім, або правильним.
У рівностороннього трикутника всі кути рівні, величина кожного з них дорівнює 60°.
Розпізнавання трикутників за кутами
Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
Гострокутним називається трикутник, у якого всі кути гострі.

Прямокутним називається трикутник, у якого є прямий кут. Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а дві інші сторони – катетами.
Наприклад: сторона АС – гіпотенуза, сторони АВ і ВС – катети.
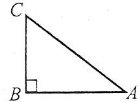
Тупокутним називається трикутник, у якого є тупий кут.
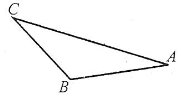
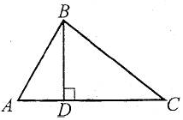
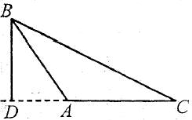
Висотою трикутника називають перпендикуляр, проведений із його вершини до прямої, яка має протилежну сторону.
Наприклад: відрізок BD – висота відповідно гострокутного, тупокутного і прямокутного трикутників.
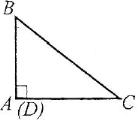
Запам’ятайте!
Види трикутників
|
За довжинами сторін: |
За величиною найбільшого кута: |
|
|
|
|
|
|
|
|
|
5.5 Побудова трикутників
Трикутник можна побудувати, якщо відома довжина кожної його сторони. Для побудови трикутника потрібні циркуль, лінійка і олівець.
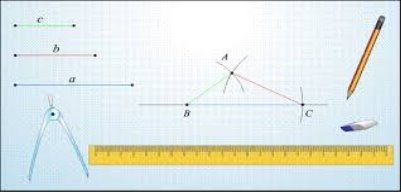
Приклад 1. Треба побудувати різносторонній трикутник ВАС з довжиною сторін: ВС = 6 см, СА = 4 см, ВА = 2 см .
Будувати треба так.
1. Провести пряму.
2. На прямій від обраної точки В відкласти відрізок , що дорівнює даному відрізку a (ВС)= 6 см, і зазначити інший кінець відрізка С.
3. Провести коло з центром С і радіусом, що дорівнює відрізку b(СА) = 4 см.
4. Провести коло з центром В і радіусом, що дорівнює відрізку c(ВА)= 2 см.
5. Точка перетину кіл є третьою вершиною А шуканого трикутника.
6. Сполучіть точки В, А, С. Назвіть знайдений трикутник. Виміряйте його сторони. Назвіть вид трикутника ВАС.
5.6 Шестикутник. Побудова правильного шестикутника
Шестикутник ( гексагон) — многокутник, що має шість вершин та шість сторін.
Шестикутник, у якого всі сторони рівні, називається правильним.
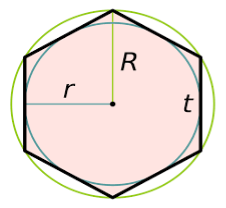

Побудова правильного шестикутника
1. Будуємо коло вибраного радіуса та проводимо його діаметр.
2. З протилежних кінців одного з діаметрів кола (наприклад, т. 1і 4)
описують дуги циркулем, розхил якого рівний радіусу кола.
3. Точки перетину цих дуг з колом, точки 2, 3, 5,6 разом з точками 1 і 4 ділять коло на 6 рівних частин.
4. З’єднавши точки 1,2,3,4,5,6 дістанемо правильний шестикутник.
Правильний шестикутник у природі, техніці та культурі.
Цікаво знати ! 

- Бджолині стільники наочно показують розбиття площини на правильні шестикутники.
- Деякі складні молекули вуглецю (наприклад, графіт) мають гексагональну кристалічну ґратку.
- Гігантський гексагон — атмосферне явище на Сатурні.
- Перетин гайки, багатьох олівців має вигляд правильного шестикутника.
- Гексаграма — шестикутна зірка, утворена двома рівносторонніми трикутниками, є, зокрема, символом юдаїзму.
- Контур Франції нагадує правильний шестикутник, тому ця фігура — символ країни. Вислів «гексагон» у французькій мові широко вживається як перифраз назви «Франція». Форма шестикутника використовується також на французьких монетах євро. Щоправда, порівняння Франції з шестикутником відносно
недавнє.
Тренувальні вправи
1. Які багатокутники ви бачите на рисунку?
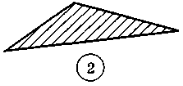
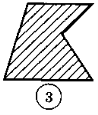
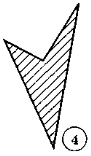
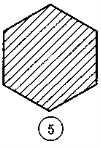
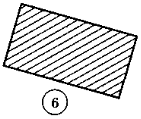
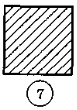
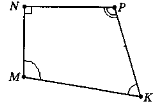
2.Спираючись на рисунок, назвіть усі вершини, усі сторони та всі кути чотирикутника MNPK. Визначте на око, чи є у цьому чотирикутнику прямий, тупий, гострий кути. Скільки яких кутів?
3.Знайдіть периметри трикутників, зображенихна рисунках (довжини сторін зазначено у метрах).
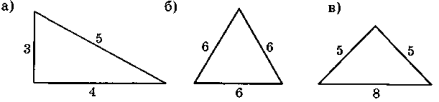
4.Накресліть чотирикутник з двома прямими кутами. Які у нього два інших кути?

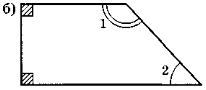
5.Накресліть: 1) чотирикутник; 2) п'ятикутник; 3) шестикутник;
4) семикутник.
6.Знайдіть периметр прямокутника, як що його сторони дорівнюють 3 см,
- см .
7.Скільки сторін, вершин, кутів у трикутника; чотирикутника; шестикутника ?
8.Серед чотирикутників, зображених на рисунках, знайдіть прямокутники.
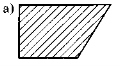
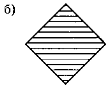
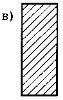
9. Скільки прямокутників на рисунках?
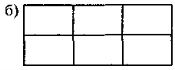
10.Якої довжини треба взяти кусок дротини, щоб зробити з нього:
а) квадрат зі стороною 3 см?
б) прямокутник зі сторонами 15 см і 4 см?
11. Побудуйте та зафарбуйте різними кольорами:
а) прямокутник зі сторонами 3 см і 5 см;
б) квадрат зі стороною 4 см.
12.Периметр квадрата 36 м. Яка його сторона?
13.Периметр прямокутника 36 см, довжина — 11 см. Знайдіть ширину пря- мокутника.
14. Заповніть таблицю для прямокутників.
|
а |
23 см |
125 м |
|
|
b |
17 см |
|
1250 км |
|
Р |
|
1000 м |
|
15.Яка площа квадрата зі стороною 9 см?
16.Яка площа прямокутника зі сторонами 5 см і 3 см?
17.10 га = ? а.
18.Периметр квадрата 20 см. Знайдіть його площу.
19.Площа прямокутника 126 см2, його довжина — 21 см. Знайдіть ширину прямокутника.
20.На рисунку зображений рівнобедрений трикутник ABC. Назвіть:
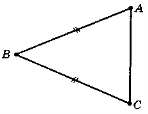 а)основу;
а)основу;
б) бічні сторони;
21.Визначте вид трикутника за його кутами:
а) 34°, 127°, 19°; в) 45°, 60°, 75°;
б) 40°, 50°, 90°; г) 95°, 85°, 5°.
22. Накресліть рівносторонній, різносторонній та рівнобедрений трикутники, позначте їх. Виміряйте сторони кожного трикутника.
23. Побудувати різносторонній трикутник ВАС з довжиною сторін: ВС = 3 см 6мм, СА = 4 см, ВА = 2 см . При допомозі лінійки виміряйте правильність побудови.
Розділ 6. Коло. Круг 
6.1 Коло
Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки — центра кола.
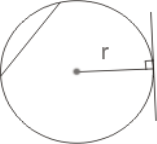
Мал. 1. Коло
Радіус кола — відстань від точок кола до його центра. Радіус кола зазвичай позначається буквами r, R.
Хорда — відрізок, який з'єднує будь-які дві точки кола. Хорда, що проходить через центр кола, називається діаметром. Діаметр рівний подвоєному радіусу кола. Діаметр зазвичай позначають буквами d, D.
Дотична — пряма, яка проходить через точку кола перпендикулярно до радіуса, проведеного в цю точку. Через будь-яку точку, що лежить поза колом і належить площині кола, можна провести дві різні дотичні.
Запам’ятайте!
Діаметр у два рази більший за радіус.
6.2 Круг
Кругом називається фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка — центр круга. Радіус — задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.
Запам’ятайте!
Коло – це замкнена крива лінія. Вона має довжину.
Круг – плоска фігура, що має площу.
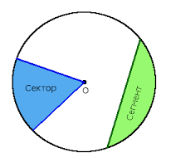
Сектором називається частина круга, що обмежена двома його радіусами.
Сегментом називається частина круга, що обмежена хордою і дугою.
Тренувальні вправи
1.Яку геометричну фігуру називають колом, кругом ?
2.Скільки в колі можна провести радіусів, діаметрів ?
3.Чи можна діаметр назвати хордою ?
4.У скільки разів діаметр більший за радіус ?
5. Накресліть кола радіусом 2см, 4 см. чому дорівнюють їх діаметри ?
6. Накресліть кола радіусами 3см 5мм, 4см 2мм, 5см. Яке з цих кіл буде найбільшим, найменшим ?
7.На колі лежать точки А, В, С. Чи на однаковій відстані вони від центра кола О ?
8.Накреслити круг довільного радіусу. Позначити в ньому сектор, сегмент.
Розділ 7. Кути
7.1 Види кутів
Частину площини, обмежену двома променями із спільним початком, називаоть кутом.
Промені ОА і ОВ називають сторонами кута АОВ, а точку О – вершиною кута.
Кути вимірюють транспортиром.
Кут, обидві сторони якого лежать на одній прямій, називають розгорнутим. Розгорнутий кут дорівнює180°
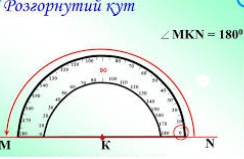
Із двох кутів більшим вважається той, міра якого більша.
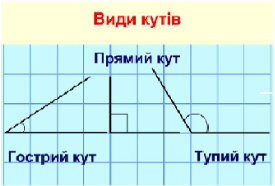
Кут в 90 градусів називається прямим кутом.
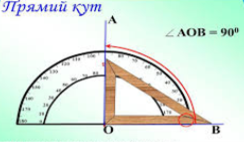
Кут менший від прямого, називається гострим кутом.
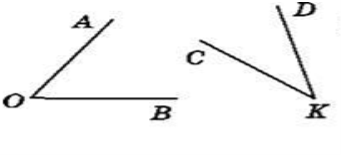
Кут більший від прямого, називається тупим кутом.
Міри кутів, як і довжини відрізків,можна додавати і віднімати.
7.2 Суміжні кути
Суміжні кути — це пара кутів, які доповнюють один одного до 180 градусів. Два суміжні кути мають спільну вершину і одну спільну сторону, дві інші (не спільні) сторони утворюють пряму лінію.
Наприклад, для кута 135 градусів суміжним є кут 45 градусів. Для кута x градусів суміжним буде кут 180-x градусів.
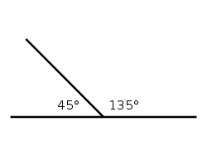
Властивість суміжних кутів: сума суміжних кутів дорівнює 180°.
Приклад 1. Знайдіть міри суміжних кутів, якщо один з них 50°.
Розв’язання . За властивістю суміжних кутів їх сума дорівнює 180°. Отже, 180°- 50°= 65°
Тренувальні вправи
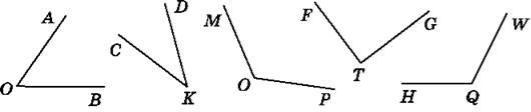
- Визначіть види кутів та накресліть їх. Запишіть сторони і вершини кутів.
2.Користуючись лінійкою і лініями в зошиті, побудуйте прямий кут.
3.У скільки разів прямий кут менший від розгорнутого ?
4.Користуючись транспортиром і лінійкою. побудуйте кут. міра якого дорівнює: а) 30°; б)55°; в)110°.
5.Міри кутів АОВ і КМР дорівнюють відповідно 65°та 135°. Знайдіть Їх суму і різницю.
6.Який кут утворюють годинна і хвилинна стрілки годинника, що показує
а) 3 години; б) 10 годин; в) 14 годин.
7. Накресли кут КРТ. Зафарбуй частину площини, яку обмежують його сторони. Вкажи вершину і сторони цього кута.
8. Накресліть розгорнутий кут. Проведіть із його вершини ще один промінь. Як називаються отримані два кути ?
9.Знайдіть міри суміжних кутів, якщо один з них 35°.
10. Визначте величину кута, якщо відомо, що суміжний з ним кут дорівнює:
а) 61°; б) 97°; в) 12°.
Розділ 8. Площа прямокутника (квадрата)
8.1 Поняття про площу
Кожний многокутник обмежує певну частину площини, яка характеризується своєю величиною – площею. Кажуть, що кожний многокутник має свою площу
Визначити площу фігури – це означає дізнатися,скільки одиничних квадратів вміщується в даній фігурі.
Квадрат, сторона якого дорівнює 1см, називається одиничним.
Площа фігури вимірюється в квадратних одиницях.
Ними є:
- Один квадратний міліметр – площа квадрата зі стороною один міліметр;
- Один квадратний сантиметр – площа квадрата зі стороною один сантиметр;
- Один квадратний дециметр – площа квадрата зі стороною один дециметр;
- Один квадратний метр – площа квадрата зі стороною один метр;
- Один квадратний кілометр – площа квадрата зі стороною один кілометр.
Для вимірювання площ ділянок на поверхні Землі користуються такими одиницями площ:
Один ар (сотка) – площа квадрата зі стороною десять метрів;
Один гектар – площа квадрата зі стороною сто метрів.
Запам’ятайте!
1 см2 = 100 мм2;
1 дм2 = 100 см2;
1 м2 = 100 дм2 = 10 000 см2;
1 ар = 100 м2;
1 га = 10 000 м2.
8.2 Площа квадрата
Запам’ятайте!
Площа квадрата дорівнює добутку двох його сторін.
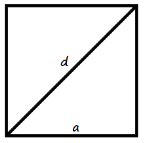
Формула площі квадрата:
S = a2, де a — сторона квадрата.
8.3 Площа прямокутника
Запам’ятайте!
Площа прямокутника дорівнює довжині, помноженій на ширину.
S = a · b
де S - площа прямокутника,
a, b – сторони прямокутника. 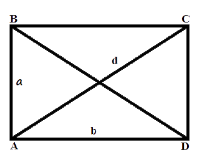
Тренувальні вправи
- Скільки сантиметрів міститься в 1дм?
- Обчислити площу квадрата зі стороною 6 м.
- Обчислити площу прямокутника, сусідні сторонни якого дорівнюють 12 см і 5 см.
- З яких геометричних фігур складається даний малюнок?

- Довжина класу 8м, ширина 8м. У класі 12 учнів. Яка площа припадає на одного учня ?
- Довжина і ширина кімнати 5м і 3м4дм. Яка площа кімнати ?
- Довжина класу 8м, ширина 8м. У класі 12 учнів. Яка площа припадає на одного учня ?
- Довжина і ширина зали 5м і 3м4дм. Яка площа зали ?
- Скільки арів має ділянка, довжина якої 60м, а ширина 50м ?
- Скільки гектарів має поле прямокутної форми, довжина і ширина якого 850м і 600м ?
- Є два квадрати. Сторона одного дорівнює 18м, а другого- 6м. У скільки разів площа першого квадрата більша за площу другого ?
- Довжина ковдри 20дм, ширина 15дм. На кожному квадратному дециметрі вишито три квітки. Скільки квіток вишито на всій площі покривала ?
- Сім’я отримала нову трикімнатну квартиру. Кімнати мають такі розміри: 5м і 3м; 6м і 3м; 3м 50см і 2м. Скільки чоловік живе в сім’ї, якщо відомо, що на одну людину надають 9кв.м ?
- Житлова площа будинку становить 10 240кв.м Частину площі одержали будівельники. 3 800кв.м – вчителі, 4 520кв.м – лікарі. Обчисліть, скільки квадратних метрів площі одержали будівельники ?
Розділ 9. Геометричні тіла
9.1 Прямокутний паралелепіпед
Прямокутний паралелепіпед – це геометричне тіло, гранями якої є шість прямокутників або чотири прямокутники і два квадрати.
Об'єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів.
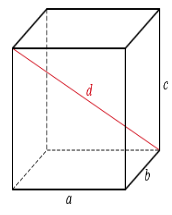
![]()
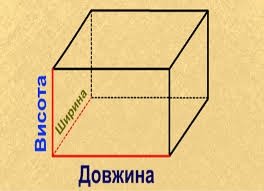
V – об'єм
S – площа поверхні
a,b,c – сторони
d – діагональ прямокутного паралелепіпеда
Властивості
1. Протилежні грані рівні і паралельні.
2. Діагоналі фігури рівні.
Предмети, що мають форму прямокутного паралелепіпеда


9.2 Куб
Куб — прямокутний паралелепіпед, у якого всі ребра рівні. Кожна грань куба є квадратом.
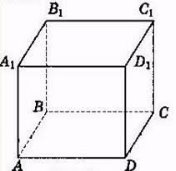
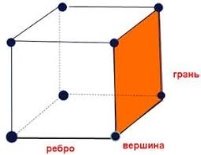
Щоб знайти об’єм куба, потрібно піднести у куб довжину ребра куба. Іншими словами, помножте довжину ребра куба саму на себе три рази.
V = a× a× a
Предмети, що мають форму куба


9.3 Піраміда
Пірамі́да — геометричне тіло. Всі грані піраміди – трикутники.
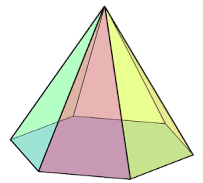
Спільну вершину трикутних граней називають вершиною піраміди, протилежну їй грань — основою, а всі інші грані — бічними гранями піраміди.
Відрізки, що сполучають вершину піраміди з вершинами основи, називають бічними ребрами.
Перпендикуляр, опущений з вершини піраміди на площину її основи, називають висотою піраміди. Висотою також називають і довжину цього перпендикуляра.
АВСD – основа піраміди. OS – висота піраміди (h).
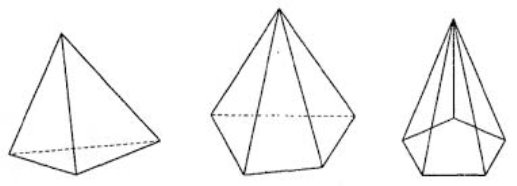
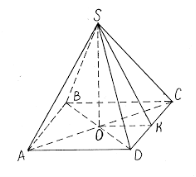 Трикутна, чотирикутна та п’ятикутна піраміди.
Трикутна, чотирикутна та п’ятикутна піраміди.
Цікаво знати !
 Піраміди в Єгипті.
Піраміди в Єгипті.

9.4 Циліндр
Цилі́ндр (грец. — «валик») — геометричне тіло, утворене обертанням прямокутника навколо його сторони.
Сторони ОА і 01В описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра. Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні і дорівнюють АВ, називаються твірними циліндра.
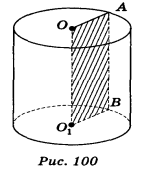 ОО1 – висота циліндра (h).
ОО1 – висота циліндра (h). 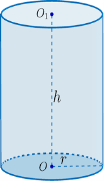
r – радіус основи циліндра.
Предмети, що мають форму циліндра

9.5 Конус
Ко́нус — геометричне тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса.
Конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів.
Радіус цього круга називається радіусом конуса; точка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.
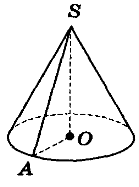
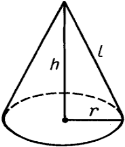

Радіус основи конуса - r. Висота конуса h . L – твірна конуса.
Предмети, що мають форму конуса




9.6 Куля
Куля — геометричне тіло, утворене обертанням круга навколо його діаметра. Центром кулі називають центр круга, обертанням якого її утворено.
Радіус кулі — це відрізок, який з'єднує точку поверхні кулі і його центр.
Діаметром кулі називається відрізок, що з'єднує дві точки поверхні кулі і проходить через його центр.
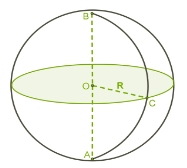

Є назва і для поверхні кулі. Її називають сферою.
Предмети, що мають форму кулі
Предмети, що мають форму кулі, оточують нас дуже часто. Форму кулі має м'яч (футбольний, тенісний, баскетбольний). Уявлення про кулю дають кавун, апельсин, горошина. Куляста і наша планета Земля.


Цікаво знати !
Перша повітряна куля була виготовлена братами Монгольф’є в 1783 році. У повітряних кулях використовується газ який легший за повітря, тому куля піднімається вгору.  Більшість куль ( оболонки) виготовлені з нейлону. Точка плавлення цього матеріалу складає приблизно 230 градусів за Цельсієм. Температура всередині кулі зазвичай нижче 120 градусів за Цельсієм. Повітряні кулі не можуть бути використані в дощ.
Більшість куль ( оболонки) виготовлені з нейлону. Точка плавлення цього матеріалу складає приблизно 230 градусів за Цельсієм. Температура всередині кулі зазвичай нижче 120 градусів за Цельсієм. Повітряні кулі не можуть бути використані в дощ.
Тренувальні вправи
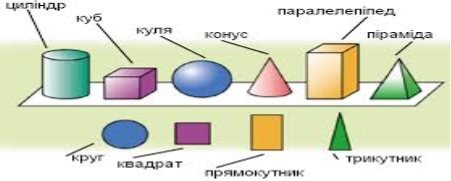
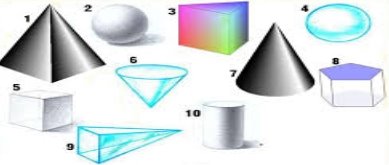
- Які геометричні тіла зображені на малюнку?
- Ребро куба дорівнює 7 м. Знайдіть об'єм куба.
- Довжина прямокутного паралелепіпеда 8 дм, ширина в 4 рази менша за довжину, а висота – 5см. Знайдіть об'єм прямокутного паралелепіпеда. .
- Довжина прямокутного паралелепіпеда 8 дм, ширина на 3 дм менша за довжину. Об'єм паралелепіпеда дорівнює 200 дм3. Знайдіть висоту.
-
Форму якого геометричного тіла має чашка?

-
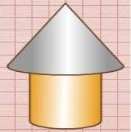
З яких геометричних тіл складається дана споруда?
- Назвіть предмети, що мають конічну форму.
Накресліть конус.
- Назвіть предмети, що мають форму піраміди.
Накресліть трикутну піраміду.
- Назвіть предмети, що мають форму циліндра.
Накресліть циліндр.
- Назвіть предмети, що мають форму кулі. Накресліть кулю.
11.Якими мірами вимірюється об’єм геометричних тіл ?
12.Ребро куба дорівнює 12смм. Знайди площу однієї його грані.
13.Знайди суму довжин усіх ребер куба, ребро якого дорівнює 8дм.
14. Знайди суму довжин усіх ребер прямокутного паралелепіпеда, виміри якого 3дм, 5дм, 7дм.
15.Ребро куба дорівнює 10 см. Знайди площу його поверхні (тобто суму площ усіх його граней).
16. Прямокутний паралелепіпед має розміри: 15см, 8см, 16см. Обчисліть
його об’єм.
17. Щоб зробити льох, викопали яму у формі прямокутного
паралелепіпеда з розмірами 2м, 4м, 4м. Скільки кубометрів землі
вийняли ?
18. Практичне завдання. Зробивши потрібні виміри, обчисли
а) об’єм сірникової коробки;
б) об’єм коробки з під чаю.
19. 1 куб. м води має масу 1т. Скільки тонн води вміщається в
резервуарі, виміри якого 2м, 2м, 4м ?
Висновок.
Навчальний посібник створено у 2018 році відповідно до Державного стандарту корекційної освіти, програм з математики для 5-10 класів спеціальних навчальних закладів для дітей з порушеннями інтелектуального розвитку, затвердженої Міністерством освіти і науки України у 2015 році та Європейського стандарту викладу інформації, яку легко читати та розуміти.
Матеріали посібника схвалено методичною радою спеціальної школи та визнано доцільними для використання на уроках математики та позаурочній діяльності. Навчальний посібник «Геометричний матеріал» апробовано на уроках математики в КЗО Жовтоводській спеціальній загальноосвітній школі.
Використані ресурси
1.Інформація для всіх: Європейські стандарти викладу інформації, яку легко читати та розуміти. Методичний посібник. – К.: ВГО «Коаліція».- 2014. – 40 с. [Електронний ресурс]: режим доступу: http://www.inclusion-europe.com/etr/
2.Брошури ISBN 2-87460-110-1,опублковані організацією Inclusion Europe за підтримкою Європейської Комісії. [Електронний ресурс]: режим доступу: www.life-long-learning.eu
3.Шумель Л.М. Збірник диктантів з геометрії. М. Дніпро, 2002р.- 17с.
4.Сисоєва С.О.Основи педагогічної творчості вчителя: Навчально-методичний посібник.- К.:ІСДОУ, 1994.-112с.
5.Хилько А.А. Математика. Підручник для 7 класу допоміжної школи.- Київ.»Освіта».-1991.-С.205-212.
6.Перова М.М, Капустіна Г.М.Математика. Підручник для 5 класу допоміжної школи. Київ. «Освіта».-1997.- С.134-137.
7.Бевз Г.П.Математика.Пробний підручник для 5 класу загальноосвітніх навчальних закладів. Київ. «Вежа».-2000.С.72-100.
8. Довідник цікавих фактів та корисних знань © dovidka.biz.ua [Електронний ресурс]: режим доступу:http://dovidka.biz.ua/tsikavi-fakti-pro-trikutnik/
Зміст
Передмова.............................................................................................3
Математичні символи та скорочення.............................................4
Розділ 1.Точка, пряма, відрізок, промінь....................................5-7
1.1 Рівність і нерівність відрізків................................................5
1.2 Додавання і віднімання відрізків..........................................6
Тренувальні вправи.............................................................6-7
Розділ 2.Ламана лінія.......................................................................7-8
- Поняття ламаної......................................................................7
- Побудова ламаної лінії...........................................................7
Тренувальні вправи.............................................................7-8
Розділ 3.Симетрія.......................................................................8-11
- Симетрія відносно точки.........................................................9
- Симетрія відносно прямої....................................................9-10
- Симетрія в природі та архітектурі......................................10-11
Тренувальні вправи................................................................11
Розділ 4. Паралельні та перпендикулярні прямі.....................11-15
- Паралельні прямі..................................................................11-12
4.2 Перпендикулярні прямі......................................................12-14
Тренувальні вправи...........................................................14-15
Розділ 5. Багатокутники (многокутники) .................................16-25
5.1 Поняття багатокутникиа (многокутника)...........................16
5.2 Паралелограм, прямокутник, ромб, квадрат та їх
властивості ..................................................................................16-18
5.3 Поняття про трикутник. Периметр трикутника..............18-19
5.4 Види трикутників................................................................19-21
5.5 Побудова трикутників........................................................21-22
5.6 Шестикутник. Побудова правильного шестикутника.....22-23
Тренувальні вправи.............................................................23-25
Розділ 6. Коло. Круг........................................................................26-27
- Коло...........................................................................................26
- Круг......................................................................................26-27
Тренувальні вправи..................................................................27
Розділ 7. Кути..................................................................................27-30
- Види кутів............................................................................27-28
- Суміжні кути.............................................................................29
Тренувальні вправи.............................................................29-30
Розділ 8. Площа прямокутника, квадрата..............................30-32
- Поняття про площу.................................................................30
- Площа квадрата......................................................................31
8.3 Площа прямокутника...............................................................31
Тренувальні вправи.............................................................31-32
Розділ 9. Геометричні тіла..............................................................32-39
- Прямокутний паралелепіпед...................................................33
- Куб.............................................................................................34
- Піраміда...............................................................................34-35
- Циліндр.....................................................................................36
- Конус....................................................................................36-37
9.6 Куля......................................................................................37-38
Тренувальні вправи..............................................................38-39
Висновок..................................................................................................40
Використані ресурси..............................................................................41
1


про публікацію авторської розробки
Додати розробку
 Різносторонні
Різносторонні Тупокутні
Тупокутні Рівнобедрені
Рівнобедрені Гострокутні
Гострокутні Рівносторонні
Рівносторонні Прямокутні
Прямокутні