Навчально-методичний посібник. Методи математичного аналізу
Відділ освіти Бучанської міської ради
Міський методичний кабінет
Бучанська Українська гімназія
МАТЕМАТИКА
Навчально-методичний посібник
ЗАСТОСУВАННЯ ЕЛЕМЕНТІВ ВИЩОЇ МАТЕМАТИКИ
ПРИ РОЗВ'ЯЗУВАННІ ЗАДАЧ
ЕЛЕМЕНТАРНОЇ МАТЕМАТИКИ
Буча — 2018
Репенко В.І. Застосування елементів вищої математики при розв’язуванні задач елементарної математики/В.І.Репенко.-Буча,2018.-34с.
Рецензенти: Т.В. Коваль, викладач математики, кандидат фізико-математичних наук НУБіП України.
І.В.Жучкова,завідуюча центром роботи з обдарованими дітьми відділу освіти Бучанської міськради.
У навчально-методичному посібнику показано, як методи математичного аналізу можна ефективно застосовувати при розв’язуванні задач елементарної математики. У посібнику містяться вправи для самостійної роботи і відповіді до них.
Нестандартне використання елементів математичного аналізу, запропоноване в посібнику, дозволяє глибше засвоїти основні поняття елементарної математики.
Посібник призначається для факультативних занять,для роботи з обдарованими учнями.Може бути використаний у школах з поглибленим вивченням математики,ліцеях,гімназіях природничо-математичного профілю та самостійної підготовки до олімпіад.
ЗМІСТ
Вступ……………………………………………………………………4
1. Доведення тотожностей------ 5
2. Доведення нерівностей .....................................9
3. Розкладання алгебраїчних виразів на множники..................17
4. Обчислення сум .........................................19
5. Розв’язування рівнянь і нерівностей ...........................23
6.Приклади для самостійної роботи-------- 29
7.Відповіді --------------------------------------34
8.Використана література--------------------- 35
Вступ
Одним із ефективних механізмів підвищення якості знань у середній школі є використання математичного аналізу при розв’язуванні задач елементарної математики. У збірнику наведено приклади, що можливо розв’язати одночасно методами елементарної математики, та з використанням елементів диференціального і інтегрального числення .Актуальність питання згідно до «Державної стратегії регіонального розвитку до 2020 року» ,що затверджене постановою Кабінету Міністрів України від 6 серпня 2014 року№385,до основних напрямків модернізації системи освіти віднесено формування системи освіти навчальних закладів для надання послуг з використання ресурсів ,забезпечення підвищення якості середньої освіти, та рівня конкуренто-спроможності вищої освіти. У сучасній освіті якість знань дисциплін природничого напрямку залежить від навичок умінь учнів аналітично відображати методи математичного аналізу до розв’язування задач. Елементи диференціального та інтегрального числення були затребувані ще за часів Галілея та Ньютона .Методи математичного аналізу, створені в XVII – XVIII століттях, тепер дуже широко використовуються в усіх галузях сучасної науки та техніки. Вивчення цих методів стало невід’ємною складовою частиною вищої освіти будь-якого природничого чи технічного профілю (а в останні часи і гуманітарного). Методи математичного аналізу можна досить ефективно застосовувати при розв’язанні задач, які звикли відносити до елементарної математики, наприклад, при доведенні тотожностей та нерівностей, при розкладанні алгебраїчних виразів на множники, при обчисленні сум, при розв’язуванні рівнянь та нерівностей. У більшості випадків саме ці методи ведуть до мети найпростішим шляхом, а іноді їх застосування є єдиною можливістю досягти успіху.
1.ДОВЕДЕННЯ ТОТОЖНОСТЕЙ
Застосування похідної для доведення тотожностей базується на відомій лемі (ознака сталості функції) :
«Для того, щоб функція була сталою на інтервалі, необхідно і достатньо, щоб її похідна дорівнювала нулю на цьому інтервалі».
Приклад 1. Довести тотожність
(x+b+c)2+(-x+b+c)2+(x-b+c)2+(x+b-c)2=4(x2+b2+c2).
Розв’язання:
Область визначення цієї тотожності – усі дійсні числа.
Розглянемо функцію
f(x)= (x+b+c)2+(-x+b+c)2+(x-b+c)2+(x+b-c)2-4(x2+b2+c2).
Знаходимо її похідну
f(x)= 2(x+b+c)-2(-x+b+c)+2(x-b+c)+2(x+b-c)-8x0
Тобто f(x) 0 для x є R. Таким чином, f(x)=С=const.
Для визначення С обчислимо значення f(x) при довільному х, наприклад, х=0. Одержуємо f(0)=0, тобто
(x+b+c)2+(-x+b+c)2+(x-b+c)2+(x+b-c)2=4(x2+b2+c2).
Приклад 2. Довести тотожність
cos2(x-a)+cos2(x-b)-2cos(a-b)cos(x-a)cos(x-b)=sin2(a-b).
Розв’язання:
Розглянемо функцію
f(x)= cos2(x-a)+cos2(x-b)-2cos(a-b)cos(x-a)cos(x-b), визначену для х є R. Знаходимо її похідну
f(x)=-2cos(x-a)sin(x-a)-2cos(x-b)sin(x-b)+2cos(a-b)cos(x-b)sin(x-a)+
+cos(x-a)sin(x-b).
Застосовуючи формули синуса подвійного аргументу і синуса суми, одержуємо
f(x)=-sin(2x-2a)-sin(2x-2b)+2cos(a-b)sin(2x-a-b)0.
Оскільки f(x) 0, то f(x) є сталою. Знаходимо значення f(x) при довільному х. У цьому випадку вигідно взяти х=а. Маємо f(а)=sin2(a-b).Таким чином, для х є R дана тотожність справедлива.
Приклад 3. Довести тотожність
cos2+cos2+cos2=1-2coscoscos,
де , , - кути деякого трикутника.
Розв’язання:
Оскільки =-(+), то cos=-cos(+), то потрібно довести наступну тотожність
cos2+cos2+cos2(+)=1+2coscoscos(+) /1/
при всіх і , для яких виконуються умови :
>0, >0, 0<+< /2/
Покажемо, що рівність /1/ справедлива для всіх +, а не тільки для тих, які задовольняють умови /2/. Розглянемо функцію
f(x)= cos2+cos2x+cos2(a+x)-1-2coscosxcos(+x)
Знаходимо її похідну
f(x)=-2cosxsinx-2cos(+x)sin(+x)+2cos(sinxcos(+x)+cosxsin(+x))=
=-(sin2x+sin2(+x))+2cossin(+2x)0.
Таким чином, f(x) =0, що доводить рівність /1/, а отже і задану тотожність.
Приклад 4. Довести тотожність
tg![]() tg
tg![]() + tg
+ tg![]() tg
tg![]() + tg
+ tg![]() tg
tg![]() =1,
=1,
де , , - кути деякого трикутника.
Розв’язання:
Використовуємо той факт, що ++=, розглянемо функцію
f(x)= tg![]() tg
tg![]() +ctg
+ctg![]() tg
tg![]() + ctg
+ ctg![]() tg
tg![]()
на інтервалі х є 0, (тут враховано, що tg(-x)=ctgx).
Знаходимо її похідну
f(x)= tg![]() (
(![]() -
-![]() )+
)+![]() -
- ![]() .
.
Після нескладних перетворень маємо
f(x)=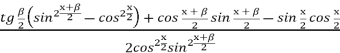 =
=
=![]() =
=
=0.
Отримали, що f(x) є сталою на інтервалі 0,. Щоб знайти цю сталу, обчислимо f(x) при х= : f()=1. Таким чином, довели, що f(x)=1 на інтервалі 0,, а звідси випливає справедливість даної тотожності.
Приклад 5. Довести, що для всіх х1 вираз 2arctgx+2arcsin ![]() дорівнює сталій. Знайти цю сталу.
дорівнює сталій. Знайти цю сталу.
Розв’язання.
Позначимо даний вираз через f(x) і знаходимо f(x):
f(x)==
Оскільки х1, то , то f(x)0 при х1. Але f(x) неперервна на півінтервалі 1,.
Приклад 6. Чи існує інтервал, на якому функція f(x)=arctgx+arctg тотожно дорівнює сталій? Якщо так, то знайдіть такий інтервал і сталу.
Розв’язання:
Обчислимо похідну
f(x)=0.
Отже, f(x)0 для всіх х, для яких функція f(x) визначена. Зауважимо, що f(x) неперервна скрізь, зокрема точки х=-1. Тому f(x)С1=const на інтервалі
-,-1 і f(x)С2=const на інтервалі -1,.
Знайдемо спочатку С2:
С2=f(1)=arctg1+arctg0=.
Знайти С1 (без таблиць) важко. Можна поступити таким чином: ми знаємо, що для всіх х<-1С1=f(x). Нехай х-, тоді arctgx - , -1,
arctg- , C1f(x) - . Оскільки С1 стала, то це можливо лише при умові, що С1=- .
Відповідь: f(x)-, x<-1,
f(x) , x>-1.
Приклад 7. Довести тотожність
1+3х2+5х4+…+(2n-1)x2n-2= ,
Розв’язання:
Оскільки
1+3х2+5х4+…+(2n-1)x2n-2=(х+х3+х5+…+х2n-1) ,
то використовуємо формулу для суми перших n членів геометричної прогресії , маємо
1+3х2+5х4+…+(2n-1)x2n-2=() .
()= = = ,
що доводить дану тотожність.
Застосування невизначеного інтегралу в тотожних перетвореннях базується на наступному: якщо дві функції F(x) і f(x) (вважаємо, для простоти, що обидві функції неперервні на а,b ) зв’язані залежністю
F(x)=f(x), x є а,b, /1/
то вони зв’язані і наступною залежністю
F(x)= . /2/
Звідси випливає, що якщо запис функції F(x) важко піддається спрощенню, то корисно спочатку розглянути її похідну. З іншого боку, два рівносильних співвідношення /1/ і /2/ показують, що запис функції f(x) можна буде спростити, якщо будемо мати простий запис для її первісної F(x).
Приклад 8. Довести тотожність
tgx+2tg2x+4tg4x+8tg8x=ctgx-16ctg16x.
Розв’язання:
Позначимо ліву частину даної тотожності через f(x).
Маємо
F(x)= ,
звідси
f(x)=F(x)=-16ctg16x+ctgx,
тобто дана тотожність справедлива.
Приклад 9. Довести тотожність
tgx+tg(x-)=3tg3x.
Розв’язання:
Позначимо ліву частину даної тотожності через f(x).
Маємо
F(x)=
Звідси f(x)=F(x)=3tg3x, що і треба було довести.
Приклад 10. Довести тотожність
sin3xsin3x+cos3xcos3x-cos2x=cos6x
Розв’язання:
Позначимо ліву частину даної тотожності через F(x).
Одержуємо
F(x)=3cos3xsin3x+3sin3xsin2xcosx-3sin3xcos3x-3cos3xcos2xsinx+sin 2x =
=-3cos2xsin4x+sin 2x=-sin 6x.
Звідси F(x)= де С – деяка константа.
Знайдемо С:
F(0)=, тобто С=0. Таким чином, F(х)=
Приклад 11. Довести тотожність
(x+a+b)3-(x+a-b)3-(x-a+b)3-(-x+a+b)3=24abx.
Розв’язання:
Позначимо ліву частину даної тотожності через F(x).
Послідовно знаходимо
f(x)=F(x)=3(x+a+b)2-3(x+a-b)2-3(x-a+b)2+3(-x+a+b)2 ,
(x)=f(x)=6(x+a+b)-6(x+a-b)-6(x-a+b)-6(-x+a+b).
Маємо (x)0. Тому f(x)=, тобто С1 = f(0)=24ab, f(x)=24ab.
Таким чином,
F(x)=, С= F(0)=0.
Одержуємо F(x)=24abx, що і треба було довести.
2.ДОВЕДЕННЯ НЕРІВНОСТЕЙ
Знання про умови монотонності функції є дуже корисними для доведення нерівностей. Якщо функція f(x) задана і неперервна в деякій зв’язаній області і має похідну в усіх внутрішніх точках цієї області, то необхідною і достатньою умовами монотонності функції в області її визначення є:
f(x)0 - для монотонно зростаючої функції,
f(x)0 - для монотонно спадної функції.
Приклад 1. Довести, що при х0
Розв’язання:
Розглянемо на проміжку 0, функцію f(x)= . Знаходимо її похідну
f(x)=
Звідси робимо висновок, що функція f(x) – зростаюча, тому для довільного х>0 f(x)> f(0)=0. Це доводить одну із даних нерівностей. Друга нерівність доводиться аналогічно.
Приклад 2. Яка величина більша:
Розв’язання:
Відповісти на це питання можна, якщо розв’язати більш загальну задачу : визначити знак нерівності ( ) для 0<a<b і 0<p<1.
Розглянемо функцію f(x)= на інтервалі 0,1. Знаходимо її похідну
f(x)=)
Легко бачити, що f(x)>0 для х є 0,1. Це означає, що функція зростає на даному інтервалі. Але f(0)=0, тому можна зробити висновок, що f(x)>0 для х є 0,1. Таким чином, ми довели, що для х є 0,1. Отже, ця нерівність буде справедливою і для х= є 0,1 ( за умовою). Маємо
Домножимо обидві частини нерівності на , одержуємо
Тепер легко відповісти на запитання задачі: .
Відповідь : .
Приклад 3 . Яка величина більша :
?
Розв’язання:
Розглянемо функцію f(x)= Оскільки f(x)= ,то
f(x)>0 при 0<x<е,
f(x)=0 при х=е,
f(x)<0 при x>е.
Таким чином, функція f(x) зростає на проміжку 0,е і спадає на проміжку е,. Отже, якщо 0<x<y<е, то
, тобто
при 0<x<y<е /1/
Аналогічно, якщо ех <y , то
при ех <y /2/
Оскільки sin = sin =, то
Слід відмітити, що з функціональних нерівностей /1/ і /2/ випливають наступні нерівності :
> , ( , , .
Приклад 4. Довести, що при 0<x< справедлива нерівність
Розв’язання:
На інтервалі 0, дана нерівність рівносильна нерівності tgx+sinx >2x, яку ми доведемо. Розглянемо функцію
f(x)= tgx+sinx - 2x .
Оскільки cosx > при 0<x< та при 0<y<1 ,то
f(x) = .
Таким чином, функція f(x) строго зростає на вказаному інтервалі, і тому
f(x) >f(0)=0, тобто при 0<x< виконується нерівність tgx+sinx >2x.
Приклад 5. Довести, що при 0<x< виконується нерівність
Розв’язання:
В силу нерівності Коші (середнє арифметичне невід’ємних чисел не менше середнього геометричного цих чисел) маємо
,
і тому достатньо показати, що на інтервалі [0,] має місце нерівність
f(x)=sinx+tgx-2x 0.
Оскільки
f(x) = cosx+>
то на [0,] функція f(x) зростає і в силу неперервності її найменше значення f(0)=0, що і треба було довести.
Приклад 6. Довести нерівність
-cosx+
і з’ясувати, коли досягаються рівності.
Розв’язання:
Розглянемо функцію
f(x)= cosx+,
f(x) - парна функція і має період 2. Знаходимо її похідну
f(x)=-sinx-sin2x-sin3x=-sin2x(1+2cosx).
Визначаємо стаціонарні точки:
f(x)=0 при sin2x(1+2cosx)=0. На проміжку 0; функція має стаціонарні точки: х=, х=. Послідовно обчислюємо
f(0)=1, f()=-, f(, f()=-.
Тепер зрозуміло, що - f(x) 1
Рівності досягаються при х=2k, х=+2k, kєZ.
Відповідь: Х=2k; +2k/ kєZ.
Приклад 7. Довести нерівність
Розв’язання:
Перепишемо дану нерівність у вигляді і розглянемо функцію
f(x)= [2;].
Знаходимо її похідну
f(x)=
Таким чином, f(x) спадає на [2;], звідки випливає нерівність, яку треба було довести.
Приклад 8. Довести, що для довільних натуральних чисел n1та k2 виконується нерівність
Розв’язання:
Перепишемо нерівність у вигляді
і розглянемо функцію
f(x)= xє1;
Знаходимо похідну
f(x)=
оскільки функція g(x)=- спадна (<0). Таким чином, одержали, що f(x) – спадна функція, звідки випливає нерівність, яку треба було довести.
Приклад 9. Не використовуючи таблиць, довести нерівність
Розв’язання:
Розглянемо функцію
f(x)= xє[-1;1]
Оскільки похідна цієї функції
f(x)=
обертається в нуль при х=0 і змінює знак з «+» на «-» при переході через цю точку, то точка х=0 є точкою максимума функції f(x). Таким чином, f(0)>f( тобто , звідки після нескладних перетворень одержуємо, що задана в умові нерівність справедлива.
Приклад 10. Довести нерівність
1+cos+
Розв’язання:
Розглянемо функцію
f(x) = 1+cosx+
f(x) – парна і періодична функція з періодом 2. Тому достатньо показати, що найменше значення функції f(x) на проміжку 0; більше за нуль. Маємо
f’(x)=sinx+sin2x+sin3x+sin4x=4sin
Знаходимо стаціонарні точки на проміжку 0;. Одержуємо
f(x)=0xє0,,
Обчислюємо значення функції в цих точках
f(0)=1+1+ f(,
f()=1-1+ f(
f(
Таким чином,
Використання інтегралів при доведенні нерівностей базується на теоремі: нехай функції f(x) і g(x) неперервні на a,b] і для всіх хєa,b] задовольняють нерівності f(x) g(x). Тоді для хєa,b]
.
Якщо строга нерівність f(x0)<g(x0),то для довільного x0 є a,b] при x> x0
З теорем виходить такий спосіб перевірки справедливості нерівності: якщо треба перевірити нерівність F(x) G(x) (хєa,b), то може виявитися корисним спочатку перевірити аналогічну нерівність для похідних цих функцій f(x) і g(x) (f(x)=F(x), g(x)=G(x)), тобто f(x) g(x) (хєa,b). Якщо остання нерівність справедлива, то справедлива і нерівність
а ліва та права частини цієї нерівності або співпадають з F(x) і G(x), або відрізняються від них на сталу.
Приклад 11. Використовуючи нерівність
sinxx (0x<), /1/
перевірити для тих же значень х справедливість нерівності
cosx1 - /2/
Розв’язання:
Проінтегруємо почленно нерівність /1/ в межах від 0 до х (0x<). Одержуємо або -cost| тобто –cosx+1.
Нерівність /2/ доведена.
Приклад 12. Перевірити справедливість нерівності
x-sinx1-cosx.
Розв’язання:
Потрібно оцінити різницю sinx – cosx. Ця різниця одержується при інтегруванні функції sinx + cosx. Враховуючи, що sinx +cosx= одержуємо, що на проміжку 0, ця функція задовольняє нерівностям
1 sinx +cosx .
Проінтегруємо останні нерівності
,
Звідки х-cosx+1+sinx, що й потрібно було довести.
Приклад 13. Відомо, що при 0х<tgxx, sinxx. Чи правильно, що для тих же значень х справедлива нерівність
tgx+sinx2x? /1/
Розв’язання:
Продиференціюємо почленно нерівність /1/:
/2/
Спочатку доведемо нерівність /2/ при 0х< Скористаємося нерівністю Коші (середнє арифметичне невід’ємних чисел не менше середнього геометричного цих чисел). Оскільки при 0х< маємо 0<cosx1, то
З нерівності /2/ при 0х< одержуємо
що рівнозначно нерівності /1/.
Приклад 14. Довести, що при справедлива нерівність
ln(2sinx)>x(-x)-2. /1/
Розв’язання:
Спочатку встановимо, що справедлива нерівність, яка одержиться, якщо почленно продиференціювати вираз /1/:
ctgx> (
Вона справедлива, оскільки випливає з правильної нерівності tg> (0<<), якщо покласти в ній =; крім того, ctg> Тому якщо проінтегрувати почленно нерівність /2/ для <x<, одержуємо
або lnsinx-ln
Після очевидних спрощень прийдемо до нерівності /1/.
3.РОЗКЛАДАННЯ АЛГЕБРАЇЧНИХ ВИРАЗІВ НА МНОЖНИКИ
Приклад 1. Розкласти на множники вираз
xy(x-y)+yz(y-z)+zx(z-x).
Розв’язання:
Розглянемо функцію
f(x)= xy(x-y)+yz(y-z)+zx(z-x), /1/
вважаючи, що х - змінна величина. Знайдемо її похідну
f(x)=2xy - z2-2zx=(y-z)(2x-y-z),
звідки
f(x)=(y-z)(x2-(y+z)x)+C,
де С не залежить від х. Покладемо в одержаній рівності х=0, враховуючи /1/ , маємо
С=f(0)=yz(y-z).
Таким чином,
f(x)=(y-z)(x2-(y+z)x)+ yz(y-z)=(y-z)(x2-yx-zx+yz)=(y-z)(x(x-y)-z(x-y))=
=(y-z)(x-y)(x-z).
Відповідь : (x-y)(x-z)(y-z).
Приклад 2. Розкласти на множники вираз
(y-z)(y+z)3+(z-x)(z+x)3+(x-y)(x+y)3.
Розв’язання:
Розглянемо функцію
f(x)= (y-z)(y+z)3+(z-x)(z+x)3+(x-y)(x+y)3, /1/
вважаючи, що х- змінна величина. Знайдемо похідну цієї функції
f(x)=-(z+x)3+3(z-x)(z+x)2+(x+y)3+3(x-y)(x+y)2=
=(z+x)2(3z-3x-z-x)+(x+y)2(x+y+3x-3y)=
=2(z+x)2(z-2x)+2(x+y)2(2x-y)=2(z3-y3+3(y-z)x2),
звідки,
f(x)=2((z3-y3)x+(y-z)x3)+C,
де С не залежить від змінної х, але може залежати від y та z. Покладемо в цій рівності х=0, враховуючи /1/, одержуємо
С=f(0)=(y-z)(y+z)3+z4-y4=2yz(y2-z2).
Таким чином,
f(x)=2(y-z)(-z2x-zyx-y2x+x3+y2z+yz2)
Далі, щоб розкласти одержаний вираз у дужках на множники, розглянемо його як функцію від у, тобто
P(y)=-z2x-zyx-y2x+x3+y2z+yz2 . /2/
Знаходимо похідну функції P(y)
P(y)=-zx-2yx+2yz+z2=2y(z-x)+z(z-x)=(z-x)(2y+z),
звідки
P(y)=(z-x)(y2+zy)+C1.
де С1 не залежить від змінної у. Покладемо у=0, тоді, враховуючи /2/, одержуємо
C1= P(0)=-z2x+x3=x(x2-z2).
Таким чином,
P(y)=(z-x)(y2 +zy)+x(x2-z2)=(x-z)(-y2-zy+x2+xz)=(x-z)(x-y)(x+y+z).
Тепер одержуємо остаточний розклад
f(x)=2(x-y)(x-z)(y-z)(x+y+z).
Відповідь : 2(x-y)(x-z)(y-z)(x+y+z).
Приклад 3. Спростити вираз
(x+y+z)3-(x+y-z)3-(y+z-x)3-(z+x-y)3.
Розв’язання:
Розглянемо функцію
f(x) = (x+y+z)3-(x+y-z)3-(y+z-x)3-(z+x-y)3 , /1/
вважаючи, що х – змінна величина, знаходимо її похідну.
f(x)=3(x+y+z)2-3(x+y-z)2+3(y+z-x)2-3(z+x-y)2=24yz,
звідки,
f(x)=24yzx+C,
де С не залежить від х. Покладемо х=0, враховуючи /1/, маємо
C= f(0)=(y+z)3-(y-z)3-(y+z)3-(z-y)3=0.
Таким чином, даний вираз дорівнює 24xyz.
Відповідь : 24xyz.
4. ОБЧИСЛЕННЯ СУМ
Нехай дані числа a1, a2, …an. Як знайти суму
Sn= a1+ a2+ …+an
Ця задача може бути розв’язана у випадку арифметичної і геометричної прогресій. У загальному випадку не завжди вдається знайти суму, і навіть у тих випадках, коли її знаходження є можливим, необхідні навички для знаходження прийомів, а саме:
- Зведення до «відомих сум». Під «відомими сумами» розуміємо суми арифметичної і геометричної прогресії, а також суми рівних степенів натуральних чисел
Sn(k)= 1k+2k+3k+…+nk, k=1,2,3…
За формулою арифметичної прогресії
Sn(1)=1+2+3+…+n=
Корисно знати і такі формули:
Sn(2)= 12+22+32+…+n2=
Sn(3)= 13+23+33+…+n3=
При підсумовуванні послідовності застосовуються властивості прогресій, метод невизначених коефіцієнтів, метод повної математичної індукції і навіть похідна.
Застосування апарату математичного аналізу дає можливість обійтися без зайвих труднощів. Це має місце тоді, коли, представляючи шукану суму як значення деякої функції при відповідному значенні аргументу, можна легко виконати підсумовування у виразі, який є похідною або первісною цієї функції.
Приклад 1. Знайти суму
352+655+958+…+93592
Розв’язання:
Оскільки 352 є значення функції y=3x2 при x=5, то можна знайти
3
Але 3 – це похідна від функції х3, а сума похідних є похідна від суми, то маємо:
(х3+х6+х9+…+х93)' = (N)' = M.
Знайдемо N= х3+х6+х9+…+х93, тобто суму геометричної прогресії де b1=x3, q=x3
N=
M=('=
Звідси 352+653+958+…+93592=
Приклад 2. Обчислити суму
Розв’язання:
Позначимо шукану суму через S. Запишемо її у вигляді S=f(), де
f(x)=x+ /1/
Розглянемо функцію f(x) на інтервалі [-1;1]. Знаходимо похідну цієї функції
f(x)=1+х+х2+…+хn-1+…=
(використали формулу суми нескінченно спадної геометричної прогресії). Оскільки |x|<1, f(x) є однією з первісних функцій , і має вигляд
f(x)=ln +C.
Визначимо сталу С. Підставляємо в останню рівність х=0. Враховуючи /1/, одержуємо
С=f(0)=0
Знаходимо S: S= f()=ln2.
Відповідь : ln2.
Приклад 3. Обчислити суми
S1=1+
S2=1+2
Розв’язання:
Розглянемо функцію
f(x)=1+2x+3x2+…+nxn-1,
де х – довільне дійсне число, крім 1, а n– довільне натуральне число; очевидно S1= f(), S2=f(6) при n=100.
Підберемо таку функцію F(x), що F(x)=f(x). Неважко переконатися, що можна взяти, наприклад, F(x)=1+х+х2+…+хn (можна, звичайно, покласти F(x)=х+х2+…+ хn або F(x)=-20+х+х2+…+ хn і т.д., в кожному з цих випадків одержуємо свій варіант розв’язування задачі). Отже, f(x)=F(x), але F(x) – сума членів геометричної прогресії, тому маємо
F(x)= (x1).
Користуючись відомими правилами диференціювання, знаходимо
f(x)=.
Таким чином, маємо
S1= f()=4-(n+2)21-n , S2=f(6)=(4996100+1) /25.
Відповідь : S1= f()=4-(n+2)21-n , S2=f(6)=(4996100+1) /25.
Приклад 4. Обчислити суму
sin
Розв’язання:
Позначимо шукану суму через S. Розглянемо функцію
f(x)=sinx+3sin3x+5sin5x+…+45sin45x.
Очевидно, що S=f(). Неважко підібрати таку функцію F(x), що F(x)=f(x). Наприклад,
F(x)=-(cosx+cos3x+cos5x+…+cos45x).
Суму F(x) легко обчислити, користуючись відомими формулами тригонометрії. Дійсно,
-2sinxF(x)=sin2x+(sin4x-sin2x)+(sin6x-sin4x)+…+(sin46x-sin44x)=sin46x
тобто F(x)= - .
Тепер знаходимо функцію f(x):
f(x) = F(x) ==.
Таким чином одержуємо шукану суму S=f(=).
Відповідь : )
Приклад 5. Обчислити суму
Розв’язання:
Позначимо суму через S. Розглянемо функцію
f(x)=
Тоді f(x)= , xf(x)=
Таким чином, шукана сума S=2f(2).
Можемо представити функцію f(x) у вигляді f(x)= (використали формулу суми геометричної прогресії). Обчислюємо похідні цієї функції:
f(x)=
f(x)=.
f(x) можна не спрощувати, а одразу обчислити f(2).
Одержуємо
S=2 f(2)=2((n+1)(n+2)2n+1-(n+1)(n+2)2n-2-(n+1)2n+3+(n+2)2n+2)=
=2n+1(n2-n+2)-4
Відповідь: 2n+1(n2-n+2)-4.
5. РОЗВ’ЯЗУВАННЯ РІВНЯНЬ ТА НЕРІВНОСТЕЙ
При розв’язуванні рівнянь та нерівностей, особливо трансцендентних, іноді потрібно дослідити функцію, яка в них входить. Цілком природно, що і тут можна застосувати апарат математичного аналізу.
Приклад 1. Розв’язати рівняння
3-sinx+tgx=5secxcos4
Розв’язання:
D(f) даного рівняння: x
Скористаємося рівністю
secx=.
Переходимо в рівнянні до tg, при цьому легко перевірити, що задане рівняння коренів не втрачає. Маємо
3- .
Позначимо tg=t, тоді одержуємо алгебраїчне рівняння 3t4-4t3+2=0. Покажемо, що це рівняння не має розв’язків . Для цього дослідимо функцію f(x)=3x4-4x3+2. Її похідна f(x)=12x3-12x2 додатна при x>1 і від’ємна при x<1. Таким чином, функція f(x) у точці х=1 приймає найменше значення. Оскільки f(1)=1, то f(x) в нуль не перетворюється, тобто початкове рівняння не має розв’язків.
Відповідь : Х=.
Приклад 2. Розв’язати рівняння
|6x-5|=4sin
Розв’язання:
Оскільки права частина рівняння не перевищує 4, то розв’язки рівняння потрібно шукати на проміжку , який визначається нерівністю |6x-5|4. Функція f(x)= |6x-5| зростає при хє і спадає при хє. В той же час функція g(x)=4sin зростає на всьому проміжку . Таким чином, на проміжку рівняння може мати не більше одного кореня. Легко показати, що х= є є розв’язком рівняння, тобто це єдиний корінь на проміжку .
Щоб знайти розв’язок на проміжку , потрібно дослідити поведінку функції f(x)=6x-5-4sin. Похідна цієї функції f(x) = 6- задовольняє нерівності f(x)6- >0 (оскільки <1), отже f(x) зростає на даному проміжку. Це означає, що f(x)<f(=0, коли х є , і х= – єдиний розвязок на цьому проміжку.
Таким чином, одержали, що рівняння має два розв’язки :
х1=, х2=
Відповідь : Х=.
Приклад 3. Розв’язати рівняння
х2-х+2=2
Розв’язання:
Перепишемо дане рівняння у вигляді
х2-2х+2=2 – х
Введемо позначення
f(x)=x2-2x+2, g(x)= 2 – х
Дослідимо ці функції на проміжку ]. Оскільки f(x)=(х-1)2+1, то ця функція досягає свого найменшого значення в точці х=1 : f(1)=1, тобто
f(x) 1 при хє]. /1/
Далі маємо
g(x)=2 2 – 1 = , (x>.
Звідси знаходимо, що g(x)>0 при <x<1, g(x)=0 при x=1, g(x)>0 при x>1.
Оскільки функція g(x) неперервна на проміжку ], то робимо висновок, що g(x) зростає при ] і спадає при ], тобто в точці х=1 функція g(x) досягає свого найбільшого значення. Отже
2 – х1 при хє]. /2/
Із /1/ і /2/ випливає, що початкове рівняння має єдиний корінь : х=1.
Відповідь: Х=1.
Приклад 4. Розв’язати рівняння
Розв’язання:
Ліва частина даного рівняння визначена на ] і невід’ємна на цьому проміжку; права частина невід’ємна на ]. Таким чином, рівняння може мати розв’язок тільки на перетині ] ]=].
Перепишемо дане рівняння у вигляді
=
Зауважимо, що на ] обидві частини рівняння зростають, оскільки
=>0, =.
При цьому <=1, >
Таким чином, початкове рівняння розв’язків не має.
Відповідь: Х=.
Приклад 5. Скільки коренів має рівняння х=а-2cos в залежності від параметра а?
Розв’язання:
Розглянемо функцію f(x)= х-а+2cos. Очевидно, що f(x)=1-sin0 для довільних хєR. Тому функція f(x) зростає на довільному проміжку між коренями рівняння sin=1, а в силу неперервності f(x) зростає на всій числовій осі. Таким чином, дане рівняння не може мати більше одного кореня. Очевидно, що f(а-3)<0, f(a+3)>0, а це означає, що f(x) =0 принаймні в одній точці проміжкуу а-3;а+3. Звідси випливає, що дане рівняння при довільному аєR має тільки один корінь.
Відповідь: дане рівняння при довільному аєR має тільки один корінь.
Приклад 6. Знайти всі значення параметра а, при яких рівняння
12х3+12ах2-8ах-3=0 має принаймні один корінь на інтервалі [0;1].
Розв’язання:
Розглянемо функцію f(x)= 12х3+12ах2-8ах-3. Зауважимо, що f(0)<0 і якщо би f(x) не мала коренів на даному проміжку, то як неперервна функція вона зберігала би знак довільних хє[0;1], тобто виконувалась би нерівність f(0)<0. Тоді повинен бути від’ємним інтеграл Але
|10=0.
Таким чином, початкове рівняння при довільних аєR має принаймні один корінь на інтервалі [0;1].
Відповідь : аєR.
Приклад 7. Розв’язати рівняння
2х9-х5+х>2
Розв’язання.
Розглянемо функцію f(x)=2х9-х5+х-2. Знайдемо її проміжки монотонності. Обчислимо похідну f(x)=18х8-5х4+1. Оскільки дискримінант квадратного тричлена 18у8-5у4+1 є від’ємним числом, то для кожного хєR маємо нерівність f(x) >0.
Таким чином, функція f(x) є неперервною і зростаючою при хєR, тому її графік може перетинати вісь ОХ тільки в одній точці. Враховуючи, що f(1)=0, робимо висновок, що розв’язком початкової нерівності є проміжок [1;].
Відповідь : хє[1;].
Приклад 8. При яких значеннях а нерівність 2(х-а)41-х має принаймні один розв’язок?
Розв’язання.
Розглянемо функцію f(x)= 2(х-а)4+х. Ті значення х, при яких minf(x)1, і будуть шуканими. Маємо f(x)=8(x-a)3+1, f(x)=0 при х=а- . Очевидно, якщо х< а- , то f(x)<0; якщо х>а- , то f(x)>0. Отже, minf(x)=f(а - )=а - . Розв’язуємо нерівність а- 1. Одержуємо а є [-;
Відповідь : а є [-;.
6.ПРИКЛАДИ ДЛЯ САМОСТІЙНОЇ РОБОТИ
Довести тотожності :
- sin3xcos3x+cos3xsin3x=sin4x
- tgx+tg(x+)+tg(x+)+tg(x+)= -4ctg4x
- arcsinx= – arccosx
- cos2(x+)+ cos2(x+)+cos2x=
- sin4x+cos2x=cos4x+
- sin2+sin2+sin2=4sinsinsin >0, >0, >0, ++=
- arcctgx+arcctg3x=arccos
Довести нерівності:
- -cosx+
- x-
- sinxx - + , 0x<
- lncosx - , 0x<
- sinx , 0x
- cosx+lncosx1-x2 , 0x<
- 2sinx+ (x- )cosx , 0x
Розкласти на множники:
- x(y2-z2)+y(z2-x2)+z(x2-y2).
- x4(y-z)+y4(z-x)+z4(x-y).
- (a-b)(a+b-c)2c+(b-c)(b+c-a)2a.
- (1+x2)y2+2(x-y)(1+xy)+1
- (x2-1)2+(y+1)(4x-y-1).
Спростити вирази:
- cos2x+cos2(x+y)-2cosxcosycos(x+y)
Обчислити суми:
- S=1+34+542+743+…+(2m-1)4m-1
- S=1+
- S= (n2 , n є N)
- S=
- S=n+(n-1)2+(n-2)4+(n-3)8+…+32n-3+22n-2+12n-1
Розв’язати рівняння та нерівності:
- Довести ,що рівняння
lnx=sinx
має на проміжку тільки один корінь.
- При яких натуральних m і n рівняння
n+cosx=(n+sinx)m
має розв’язки?
- Довести, що рівняння
x3+9x2+2x-48=0
не має кратних коренів.
- Знайти всі значення а, при кожному з яких рівняння
3x4+4x3-6x2-12x+a=0
має два різних корені.
- Розв’язати рівняння
х2+х+=36
- Знайти всі значення а, при кожному з яких рівняння
х3+ах+2=0
має два однакових корені.
- Розв’язати нерівність
log5(1+>log16x
- Розв’язати нерівність
х27+х18+448<0
Відповіді:
17. (z-y)(x-y)(x-z)
18. (y-z)(z-x)(y-x)(x2+y2+z2+xy+xz+yz)
19. b(a-c)(a+c-b)2
20. (xy-y+1)(xy+2x-y+1)
21. (x2+2x-y)(x2-2x+y+2)
22.
23. 3.
24.
25.
26. sin2y
27. S=(5+(6m-5)4m)
28. S=6-1052-50
29. S=16-(n2+3n+4)22-n
30. S=6-(n2+4n+6)2-n
31. S=2n-1(4-(n+2)21-n
33. Якщо m=1 , то n є N
Якщо m=2 , то n=1,2
Якщо m3 , то n=1
35. а є [-;11]
36. Х=3
37. а= - 3
38. х є [0;16]
39. х є [ - ; - ]
ВИКОРИСТАНА ЛІТЕРАТУРА
1. Виленкин Н.Я., Мордкович А.Г. Производная и интеграл. Пособие для учителей. – М.: Просвещение, 1976.
2. Вища математика. Загальний курс: Збірник задач та вправ. / А.Д.Тевяшев, О.Г.Литвин. — Х.: Рубікон, 1999.
3. Макуха А.С., Покровский В.С., Ушаков С.П. Математика. Письменные экзаменационные работы: Справочное пособие. – К.: Вища школа, 1977.
4. Математика в школе: Научно-методический журнал. – М.: Педагогика. - №3, - 1997.
5. Математика в школе: Научно-методический журнал. – М.: Педагогика. - №6, - 1977.
6. Математика для економістів : навч. посіб. У 3 ч. Ч. 1 / І.О. Ластівка, В.С.
Коновалюк, І.В. Шевченко [та ін.]. – К.: НАУ, 2012. – 432 с.
7. Математика для економістів : навч. посіб. У 3 ч. Ч. 2 / І.О. Ластівка, Н.І. Затула, Є.Ю. Корнілович [та ін.]. – К.: НАУ, 2012. – 312 с.
8. Математика для економістів : навч. посіб. У 3 ч. Ч. 3 / І.О. Ластівка, В.В. Михайленко. – К.: НАУ, 2012. – 272 с.
9. Математичний аналіз у задачах і прикладах. У 2 ч. : навч. посібник/ Дюженкова Л. І., Лященко М. Я. та ін. – К. : Вища школа, 2003. – Ч.1.
10. Нестеренко Ю.В., Олехник С.Н., Потапов М.К. Задачи вступительных экзаменов по математике. - М.: Наука, 1983.
11. Соколенко О.І., Новик Г.А. Вища математика в прикладах і задачах. – К.: ”Либідь”, 2001 р.
12. Фадеев Д.К., Никулин М.С., Соколовский И.Ф. Элементы высшей математики (для школьников). – М.: Наука, 1987.
1


про публікацію авторської розробки
Додати розробку
