Навчання розв'язування задач методом графічного моделювання

Навчання розв'язуванню задач методом графічного моделювання

Стратегiя розвитку освiти в Українi вiдповiдно до нацiональної програми «Освiта» передбачає використання свiтового досвiду для створення системи освiти, яка б вiдповiдала стандартам ХХI столiття. Розвитку математики i математичнiй освiтi у нашiй країнi придiляється велика увага. У школi на вивчення математики вiдводиться 15-20% навчального часу. Мiльйони молодших школярiв вивчають початки математики пiд керiвництвом класовода. Вчитель початкових класiв – це вчитель математики.

Щоб бути справжнiм профiсiоналом учитель має не лише орiєнтуватися в широкому спектрi сучасних iновацiйних проектiв, iдей, рiзних моделей шкiл, а й мати у своєму арсеналi найефективнiшi освiтнi технологiї.

Мені хотілося б звернути увагу на досягнення педагогів-новаторів та інноваційні підходи вчителів при викладанні математики. Інноваційна освітня діяльність характеризується пошуком нових чи вдосконалених концепцій, принципів, підходів до освіти, суттєвою зміною у змісті, формах і методах навчання та виховання, управління навчально-виховним процесом, зокрема в загальній освіті. За визначенням, освітня інноваційна діяльність передбачає розвиток творчого потенціалу учасників навчально-виховного процесу, зміни в способі їхньої діяльності та стилі мислення, створення та поширення новизни в системі освіти.

Щодо розвитку творчого потенціалу учасників навчально-виховного процесу та зміни в стилі їхнього мислення, то встановлено, що рівень педагогічної діяльності вищий у тих закладах освіти, які активніше беруть участь в експериментально-дослідній (інноваційній) діяльності.

Сьогодні вчителі працюють над методичним збагаченням уроків. Однак, дидакт О.Я. Савченко зазначає: «В організації уроку творчий пошук учителя необхідний, водночас підкреслимо, що новації – не самоціль, і вони мають бути педагогічно виправданими й відповідати основним вимогам навчання і виховання в сучасній початковій школі» [ 1].

Спостереження за шкільною практикою у початкових класах показали, що деякі вчителі недооцінюють значення прийомів організації творчої роботи над задачами. Мають місце певні складності в застосуванні цих прийомів. Більшість вчителів початкових класів використовують традиційні прийоми у навчанні розв’язування задач. Без сумніву, така робота потребує багато часу на уроці. Формування вмінь записувати коротко задачу, швидко обчислювати – необхідний елемент в навчанні математики, а також мета навчання. Щоб досягнути цієї мети можна використовувати такий вид роботи, як графічне моделювання задач.

Моделювання задачi — це використання специфiчних предметiв та знакiв, якими замiнюються ї числовi данi, зображуються зв'язки i залежностi мiж даними i невiдомим, причому iз згаданими предметами та знаками учнм мають бути ознайомленi i використовувати їх у навчальнiй діяльності (малювати, креслити у зошитi, виконувати практичнi дiї – розрiзати на частини, порiвнювати, складати з окремих частин цiле, тощо). Моделювання при розв'язаннi задач допомагає учням творчо проявити себе, а також без усиль знайти правильну вiдповiдь. Обчислювальнi прийоми замiнюються графiчними, застосовуються схематичнi малюнки. Вони або вiдразу приводять до потрi бного результату, або значно полегшують пошук способу розв'язання задач. Графiчне моделювання математичного змiсту задачi допомагає побачити яких саме даних не вистачає (або якi зайвi), з'ясувавши потрiбну залежнiсть легко знайти шуканий результат. Нарештi, правильно побудованi графiчнi моделi умов задач у багатьох випадках дають змогу учням зробити «прикидку» очiкуваної вiдповiдi, а також перевiрити правильнiсть арифметичного розв'язання задачi.

 

Отже, графічне моделювання задач сприяє розвитку навичок обчислення, навичок креслення, каліграфії, розвитку розумових здібностей, вмінню аналізувати, порівнювати, узагальнювати, а також сприяє розвитку творчих здібностей дитини.

Наприклад, розв’язуючи задачу на збільшення (зменшення) числа на декілька одиниць, можна побудувати наступні схеми-моделі (див. рис. 1, 2), за допомогою яких діти швидко запам’ятовують умову задачі, виявляють величини, про які йдеться в задачі та  з’ясовують зв’язки між ними, на основі яких обиратимуть дії.

Задача 1. У Сергія було 4 яблука, а в Колі на три яблука більше. Скільки яблук було у Колі?

 

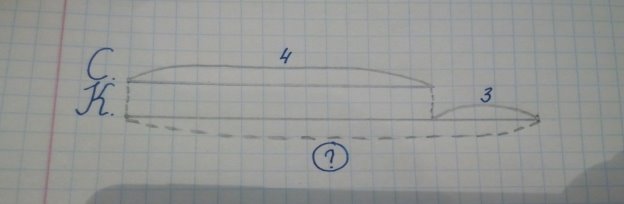
Рис.1. Схема-модель №1

Діти, будуючи схему-модель, міркують так: до яблук Сергійка слід додати ще три яблука, бо в умові сказано, що в Колі на 3 яблука більше, а це значить, що в нього було стільки, скільки у Сергійка та ще 3 яблука.

Після такого аналізу діти вибирають дію додавання і розв’язують задачу так:

4+3=7 (ябл.)

Відповідь: 7 яблук у Колі.

Задача 2. На гілці було 9 груш. Три груші впали на землю. Скільки груш залишилося на гілці?

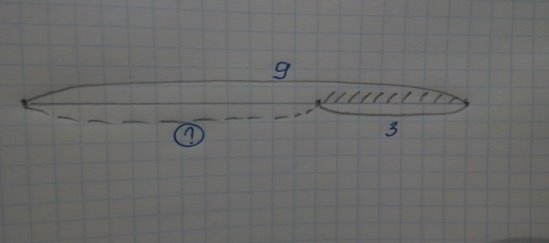
Рис. 2 Схема-модель №2

Будуючи схему , діти міркують так: було 9 груш, 3 – упало. Отже, на гілці має залишитися менша величина, ніж була.  Тому треба від тієї величини, що була, забрати ту величину, що упала. З цього міркування діти вибирають дію віднімання:

9-3=6 (груш)

Відповідь: 6 груш залишилося на гілці.

Серед різноманітних видів задач хочеться відзначити складені типові задачі, наприклад, на знаходження четвертого пропорційного, на пропорційний поділ, на знаходження невідомого за двома різницями, адже при розв’язанні саме цих задач учні зазнають деякі труднощі. Їм важко оперувати тими компонентами, які є логіко-математичною структурою розв’язання задач. Водночас діти досить впевнено виконують первинний аналіз тексту задачі, що відображає конкретні, добре зрозумілі їм життєві ситуації (переказують текст, називають дані й шукані величини тощо), уміють виконувати математичні операції. Згадані труднощі певною мірою зумовлені важливою особливістю розумової діяльності дітей: під час навчання перехід від стадіях виконання конкретних операцій (на основі яких може відбуватися систематизація властивостей даних у безпосередньому наочному досвіді) до стадії виконання формальних операцій (які пов’язані з первинним рівнем розвитку здібностей до узагальнення й абстрагування) відбуваються поступово. А тому час сприймання та розв’язування учнями задач виникає розрив між конкретною ситуацією, описаною в умові задачі, й абстрактною логіко-математичною структурою її розв’язання. Щоб усунути цей розрив, доцільно конкретизувати математичну структуру задачі за допомогою її моделювання.

Проілюструю схему-модель, що використовується при розв’язання таких типів задач, як, наприклад, задача на знаходження четвертого пропорційного з ускладненням, котра розв’язується способом зведення до одиниці.

Задача (4 клас). На пошиття 12 однакових платтів витратили 48м тканини. На сарафан витрачають на 1 м тканини менше, ніж на плаття. Скільки потрібно тканини на пошиття 18 сарафанів?

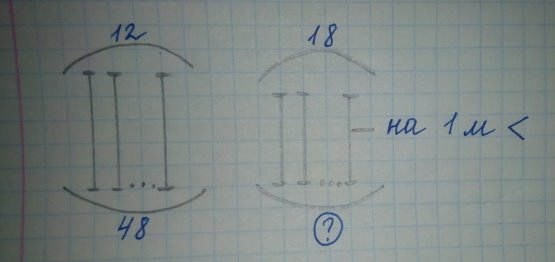
Рис. 3

1. 48:12=4 (м) – витратили на 1 плаття;
2. 4-1=3 (м) – витратили на 1 сарафан.
3. 3*18=54 (м)

Відповідь: 54 м тканини потрібно для пошиття 18 сарафанів.

При використанні такої моделі учні одразу мають наочне уявлення про відношення між даними та шуканими даних величин.  При такому моделюванні вибір дій буде зрозумілим та обґрунтованим.

За допомогою схем-моделей можна закріплювати вміння розв’язувати задачі вивченого виду. Наприклад, за даною схемою скласти умову задачі або змінити запитання задачі.

Задача 4.За схемою, поданою на рис.4, скласти умову задачі.

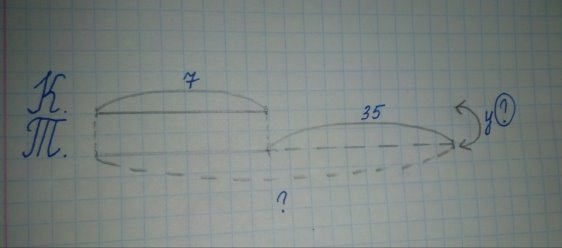
Рис.4

Схема-модель№4. Маса козеняти 7 кг, а маса теляти на 35 кг більше. У скільки разів маса теляти більше, ніж маса козеняти?

Якщо діти склали умову задачі за цією схемою,то вони орієнтуються в її розв’язанні.

Прочитавши умову задачі й розглянувши схему, учні змінюють запитання задачі: У скільки разів маса козеняти менша маси теляти?

Задача 5 (ускладнена) . у крамниці було 15 білих сумок й 12 чорних. Протягом дня продали 8 білих сумок і 4 чорних. Використовуючи цю схему постав питання до задачі і дай на них відповіді. Які ще можна поставити питання до цієї задачі?

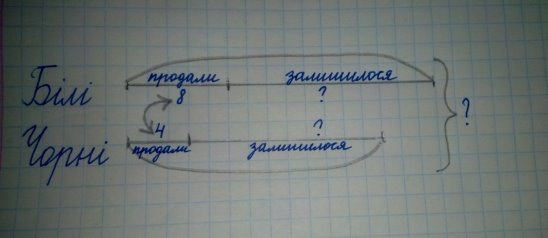
Рис. 5 Схема-модель №5

Отже, учні, розв’язуючи задачу, не тільки роблять обчислення, а й дивлячись на схему, творчо працюють.

Як бачимо, моделювання пов’язано з наочністю, яку широко використовує традиційна дидактика. Досвід передових учителів і наукові спостереження показують, що навчання учнів моделювати задачі під керівництвом вчителя потрібно практикувати вже на перших уроках математики. Відомо, що більшість дітей приходить у школу з певним рівнем розвитку пізнавальних мотивів, гострим інтересом до навчання. Вони мають деякі уявлення про число, володіють певним досвідом лічби, відділяють нове від вивченого, знають, що в школі їхні математичні знання будуть поглиблюватися. У них є установка: до школи йти, щоб вчитися, щоб пізнавати нове. А носієм цього нового, цікавого є вчитель.

Література

1. Савченко О.Я. Сучасний урок у початкових класах. – К.: «Магістр-S», 1997.

 

 

 

 

 

 

 

Як правило, у процесі аналізу використовуються лише різні види короткого запису умови чи задачі готові схеми, а створення моделі на очах у чи дітей самими дітьми в процесі розбору задачі застосовується вкрай рідко. До того ж при фронтальному аналізі і розв’язанні задачі вчителі нерідко обмежуються правильними відповідями двох-трьох учнів, а інші записують за ними готові розв’язання без глибокого їхнього розуміння.

Для усунення відзначених недоліків необхідно насамперед рішуче поліпшити методику організації первинного сприйняття й аналізу задачі, щоб забезпечити усвідомлений і доказовий вибір арифметичної дії всіма учнями. Головне для кожного учня на цьому етапі — зрозуміти задачу, тобто усвідомити, про що ця задача, що в ній відомо, що потрібно довідатися, як зв'язані між собою дані, які відносини між даними і шуканими і т.п. Для цього необхідно з I класу учити дітей розбивати текст задачі на частини і моделювати ситуації, відбиті в задачі.

Так, у II класі, вперше аналізуючи задачу: «У перший день для ремонту школи привезли 28 колод, а в другий день привезли на 4 машинах по 10 колод. Скільки усього колод привезли за ці два дні?», звичайно записують її коротко в такому виді:

I д. - 28 к.

                                                            ?

      II д. - на 4 маш. по 10 к.          

 

Така модель не відбиває життєвої ситуації з достатньою наочністю, що і приводить до помилок у розв’язанні задачі. Тому необхідно змоделювати її умову у виді схематичного малюнка:

 

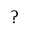І д. -  28 к. 

                                                                                                                             

ІІд. – 10 к.    10 к.  10 к.   10 к. 

 

Або графiчної схеми-моделi:

                         28к.

__________________________

       10к.                                                                     ? к.

___________________________________

 

 

 

Такi моделi відбивають математичну ситуацію більш наочно. По таким моделям навіть слабкий учень зможе записати розв’язання, якщо не так:

28+10 х  4=68 (к.), то хоча б так:

 

1. 10+10+10+10=40 (к.)

2) 28+40=68  (к.)

і викликатиме менше труднощів при повторному розв’язанні цієї чи подібної задач.

Розглянемо другу задачу: «На фермi працюють 37 трактористів, шоферів на 8 більше, ніж трактористів, а комбайнерів на 5 менше, ніж шоферів. Скільки комбайнерів працює на фермі?» Звичайний короткий запис цієї задачі виглядає так:

Т.— 37 ч.

Ш.— ?, на 8 більше

К.— ?, на 5 менше    

Такий запис при первинному аналізі цієї задачі нераціональний, тому що не розкриває наочно взаємини величин і не допомагає у виборі дій.

Така модель дає наочне представлення про зв’язок між даними і шуканим у задачі. Аналізуючи задачу, діти з'ясовують, що шоферів на 8 більше, ніж трактористів, тобто їх стільки ж так ще 8. Тому відрізок на схемі, що зображує чисельність шоферів, вони накреслять більшої довжини, чим відрізок, що зображує чисельність трактористів. А тому що чисельність комбайнерів на 5 менше, ніж шоферів, тобто їх стільки ж, але без 5, те і відрізок, що показує чисельність комбайнерів, повинний бути менше відрізка, що показує чисельність шоферів. При такім моделюванні вибір дій буде зрозумілий і обґрунтований, учні не будуть діяти навмання, механічно маніпулюючи числами.

Розглянемо задачу з пропорційними величинами:

 «У трьох однакових ящиках 21 кг апельсинів. Скільки кілограмів апельсинів у 8 таких ящиках?»

Звичайна умова цієї задачі відразу записується у таблицю:

Маса одного ящика	Кількість ящиків	Загальна маса
Однакова	3	21
	8	?

 

Таблиця — це теж модель задачі, але більш абстрактна, ніж графiчна, яка допомагає учням краще усвідомити знання взаємозалежностей пропорційних величин, тому що сама таблиця цих взаємозалежностей не показує. Тому при початковому ознайомленні з такою задачею таблиця мало допомагає уявити математичну ситуацію і вибрати потрібну дію. При початковому знайомстві з цією задачею доцільніше змоделювати її умова по-іншому, у виді схематичного малюнка чи креслення.

 

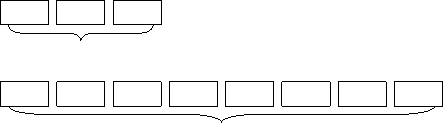
                 21 кг

 

        

 

По такій моделі шлях розв’язання задачі став би більш зрозумілим для всіх учнів: щоб довідатися, скільки кілограмів апельсинів у 8 ящиках, потрібно знати, скільки кілограмів апельсинів в одному ящику.

Особливо велику роль відіграє моделювання при розв’язанні задач на рух. При цьому модель повинні створювати самі учні під керівництвом учителя.

Задача: «Із двох міст, що знаходяться на відстані 520 км, одночасно вийшли назустріч один одному два потяги, що зустрілися через 4 год. Один потяг рухався зі швидкістю 60 км/год. З якою швидкістю рухався другий потяг?»

Вчитель у розмові з учнями з'ясовує, про який рух говориться в задачі, що про цей рух відомо, і пропонує накреслити схему руху. Викликаний учень, повторюючи зміст задачі, моделює описану в ній життєву ситуацію. Відстань між містами він зображує у виді відрізка. Напрямок зустрічного руху показує стрілками, а місце зустрічі позначає прапорцем. На питання вчителя, як позначити на схемі, що потяги зустрілися через 4 год, учень відзначає число годин руху кожного потяга вертикальними штрихами на схемі, а також позначає цифрами відстань між містами і швидкість руху першого потяга. Схема здобуває вид.

 

Розв’язання задачі дітям було запропоновано записати самостійно чи виразом по діях і пояснити вибір дії. Усі справилися з розв’язанням задачі самостійно. Учні розв’язали задачу двома способами і записали такі вирази: (520—60 х 4):4, 520:4—60.

Таке моделювання, коли модель виникає на очах у дітей, має явну перевагу перед застосуванням готових малюнків і схем.

На графічне моделювання не слід шкодувати часу на уроці. Це з лишком окупиться в процесі розв’язання задачі. І навпаки, відсутність графічної моделі може привести до неправильного розв’язання задачі. Так, в одному класі розглядалася задача: «З пачки взяли 18 зошитів, після чого в пачці залишилося в 2 рази менше зошитів, ніж було. Скільки зошитів було в пачці спочатку?» Вчитель обмежився коротким записом задачі:

Узяли    — 18 з.

Залишилося    — у 2 рази менше

Було —  ?

Потім пішло колективне розв’язання: 18:2+18=27 (з.), що невірно.

Вчитель і учні не звернули уваги на те, що в пачці залишилося в 2 рази менше, ніж було, а не чим узяли. А якби при аналізі задачі була зроблена графічна модель, те помилки не відбулося б, тому що на схемі було б видно, що залишилася половина того, що було. Виходить, у пачці було 18 х 2=36 (з.)

 

Взяли 18 з.                      Залишилосяв 2 рази менше, 

                                               ніж було             

 

Таким чином, щоб діти краще уявляли собі життєву ситуацію, розкриту в задачі, легше встановлювати залежності між величинами, а вибір дії ставав для них усвідомленим, необхідно систематично навчати дітей моделюванню, починаючи з повного предметного зображення числового взаємини величин з демонстрацією самої дії задачі. Потім варто переходити до більш узагальненого умовно-предметного і графічного моделювання, до короткого запису задачі з використанням створюваного на очах у дітей і самих дітей креслення, схеми, після чого можна переходити до більш високого ступеня абстракції з застосуванням готових узагальнених опорних схем і таблиць.

Систематичне використання предметного і графічного моделювання забезпечить більш якісний аналіз задачі, усвідомлений і обґрунтований вибір необхідної арифметичної дії і попередить багато помилок у рішенні задач учнями.