Методика навчання алгебраїчному методу розв’язування текстових задач

 

План

1. Аналіз програм та діючих підручників і навчальних посібників з алгебри

2. Методичні вимоги до навчання розв’язання текстових задач

3. Методичні основи навчання учнів алгебраїчному методу розв’язування текстових задач

4. Формування вмінь розв’язувати текстові задачі на:

    4. 1. спільну роботу

    4. 2. рух

Висновки

 

1. Аналіз програм та діючих підручників і навчальних посібників з алгебри

Необхідність спеціальної роботи з формування в учнів умінь розв'язувати задачі за допомогою рівнянь врахована у побудові діючих підручників для 7—9-х класів, де цьому питанню присвячено окремі пункти (стосовно лінійних рівнянь і їх систем, квадратних і раціональних рівнянь, систем рівнянь другого степеня).

Одночасно в підручниках чітко простежується використання задач як допоміжного засобу для формування нових понять. Наприклад, у 7-му класі за допомогою задачі вводиться поняття про систему рівнянь з двома змінними. [3].

Задача. Зошит і олівець разом коштують 96 к., причому зошит на 16 коп. дорожчий за олівець. Скільки коштує зошит і скільки олівець?

Розв’язання:

Цю задачу можна розв’язати арифметичним способом (за допомогою дій) або склавши рівняння з однією змінною. Можна розв’язати її іншим способом.

Нехай зошит коштує х к., а олівець – у к. За умовою задачі разом вони коштують 96 к., тобто

х + у = 96.

Оскільки зошит дорожчий за олівець на 16 к., то

х – у = 16

Маємо два рівняння з двома змінними. Щоб розв’язати задачу, треба знайти такі значення змінних х і у, які б одночасно перетворювали у правильну рівність кожне з рівнянь х + у = 96 і х – у = 16, тобто знайти спільні розв’язки цих рівнянь.

Якщо треба знайти спільний розв’язок двох (або більшої кількості) рівнянь, то кажуть, що ці рівняння утворюють систему рівнянь. Записують систему рівнянь, об’єднуючи їх фігурною дужкою {. Складену за умовою задачі систему лінійних рівнянь з двома змінними записують так:

Пара значень змінних х = 56, у = 40 є розв’язком кожного з рівнянь системи, бо обидві рівності 56 + 40 = 96 і 56 – 40 = 16 правильні. Таку пару чисел називають розв’язком системи. [3; 7; 9].

У 8-му класі прикладом такого підходу може бути розгляд задачі, на основі якої вводиться поняття про розв'язування системи нерівностей з однією змінною.

Розв'язування задач складанням рівнянь сприяє кращому засвоєнню учнями понять «рівняння», «корінь рівняння», «система рівнянь», «розв'язок системи рівнянь». [2; 3].

 

2. Методичні вимоги до навчання розв’язання текстових задач

Розв’язати задачу – це означає виконати те, що вимагається в задачі. Внаслідок розв’язування задач на обчислення, побудову або дослідження дістають розв’язок. Внаслідок розв’язування задачі на доведення дістають не розв’язок, а підтвердження сформульованого в задачі твердження.

Не треба плутати «розв’язок», «розв’язання» і «розв’язування». Це різні поняття.

Перше з них означає кінцевий результат розв’язування, відповідь, або частину відповіді, друге – логічну конструкцію, сукупність всіх міркувань, що приводять до потрібного висновку; третє – процес міркування.

Бажаючи зекономити час, учителі починають розв'язувати задачу, хоч багато учнів ще не засвоїли її змісту. Цьому сприяють пропозиції окремих методистів - читати умову задачі тільки раз. Наприклад, у кількох посібниках є така пропозиція:

«Повторне читання умови треба допускати тільки у виключних випадках, коли умова дуже складна. Якщо учні знають, що умова задачі буде прочитана два-три рази, то вони до першого читання ставляться без потрібної уваги».

З цією пропозицією ми не погоджуємося. Звичайно, треба добиватись, щоб під час читання учні були особливо уважні. Якщо учні неуважні, задачу читати не можна. І не треба читати її багато разів. Але задачу середньої складності, яка складається з двох речень, слід прочитати декілька разів. При першому читанні учні ознайомлюються з задачею в загальних рисах, а при другому — поглиблено її вивчають. Другий раз доцільно читати частинами, одночасно записуючи числові дані. Іноді вже в процесі розв'язування корисно ще раз прочитати умову і вимогу. Зрозуміло, що, прочитавши задачу навіть два рази, учитель не може бути впевнений, що всі учні її зрозуміли. Тому корисно запропонувати одному - двом учням повторити її або хоч відповісти на запитання: що відомо і що треба знайти.

Тільки тоді, коли всі учні добре зрозуміють задачу, можна починати її розв'язувати.

Розв’язок задачі буває правильним і неправильним, точним і наближеним, загальним і частинним. Розв’язування буває усним і письмовим, самостійним і колективним і т.д. Розв’язання кожної задачі повинно бути:

1) безпомилковим;

2) обґрунтованим;

3) повним;

4) раціональним.

Безпомилкове розв’язання

Безпомилковим вважають таке розв’язання, яке не містить ніяких помилок. Помилки в розв’язаннях математичних задач бувають в обчисленнях, в тотожних перетвореннях, побудовах, логічного характеру і т. ін. Для кожного виду задач характерні свої помилки. Наприклад, розв’язуючи задачі на доведення, часто допускають помилки хибної основи, хибного слідування, поспішного висновку, підмінюють доводжувану тезу.

Залежно від ступеня важливості в школі прийнято розрізняти грубі помилки, негрубі помилки і недоліки.

Грубими називають ті помилки, які свідчать, що учень не засвоїв основ теорії, не знає найважливіших правил, теорем, формул. [2].

Приклад грубої помилки

Негрубими слід вважати, наприклад, помилки в обчисленнях чи перетвореннях, допущені внаслідок неуважності, неправильне вживання символів.

До недоліків звичайно відносять:

а) записи відповідей у вигляді, що допускають спрощення;

б) допущені описки, неточності, які не являються наслідком незнання або не розумінням вивчення матеріалу;

в) виправлення зроблені учнями.

Обґрунтованість розв’язання

Якщо учень знайде розв’язок, але не обґрунтує його, то не можна вважати, що він справився з задачею.

У молодших класах учні часто навіть не відчувають потреби в обґрунтуваннях. Трапляються випадки, що вони ототожнюють розв’язування задачі з угадуванням. Якщо, наприклад, запитати 6 – ти класників, просте чи складене число 1021, вони, пересвідчившись, що це число не ділиться ні на 2, ні на 3, ні на 5, відповідають, що це число просте. Така відповідь правильна, але не обґрунтована.

Учні старших класів розуміють, що при розв’язувані задач треба кожний крок обґрунтувати, але часто не роблять цього, бо вважають, що «це і так очевидно».

Зрозуміло, що вимагати від учнів у кожному розв’язанні обґрунтовувати кожний крок було б не розумно. Деякі моменти розв’язання задачі, які справді очевидні, і ті, які учні вже обґрунтували раніше, можна залишати без обґрунтування. Але залишати необґрунтованими зовсім неочевидні положення в розв’язання з повним поясненням не можна.

Проте на етапі відшукання способу розв’язування задачі недоцільно вимагати від учнів обґрунтовувати кожний крок. Якщо напрям міркувань правильний, то хоч деякі моменти учні й залишають необґрунтованими, проте не слід відразу примушувати їх усе обґрунтовувати, бо це може тільки загальмувати процес розв’язування. А вже після того, як буде знайдено спосіб розв’язання, бажано запропонувати довести те, що спочатку приймали без доведення.

Повнота розв’язання

Якщо, наприклад, рівняння має кілька розв’язків, а учень знайде тільки один з них, таке розв’язання не можна вважати закінченим; воно неповне. Це саме стосується не тільки рівнянь, а й багатьох інших задач.  [2; 3].

Раціональність розв’язання

Одну задачу часто можна розв’язати кількома різними способами. Деякі з цих способів простіші, швидше ведуть до мети; інші, навпаки, складні і громіздкі. Той спосіб розв’язання, який швидше веде до мети, називають раціональнішим.

Оформлення розв’язання задач

Розв'язання задач звичайно записують у зошитах і на дошці. Якщо розв'язують задачу з шкільного підручника, то переписувати її повністю, особливо коли вона громіздка, не слід. Досить позначити її номер (наприклад, 25, або № 25, але не N 25 або ), а умову записати скорочено. Приклади краще переписувати повністю. Погано, коли в зошиті записано лише номер і відповідь.

Якщо розв'язують задачу не з шкільного підручника, а з якого-небудь посібника або складену учителем чи учнями, то її формулювання треба повністю переписати в зошит. Потім бажано написати «Розв'язання» (але не «Рішення» і не «Розв'язок», як пишуть деякі учні).

Саме розв'язання задачі можна давати без пояснень, тобто записати в основному тільки вирази, перетворення, дії, не супроводжуючи їх словесними поясненнями, і з поясненнями, поданими у вигляді зв'язаної розповіді або запитань. Дуже громіздких пояснень вимагати від учнів не слід. Інколи в роботах випускників розв'язання однієї задачі подано на п'яти - шести сторінках. Тоді мимоволі виникає питання: кому це потрібно? Велика за обсягом робота з математики ще не свідчить про добру математичну підготовку. Навпаки, у такій роботі звичайно буває багато зайвого, що швидше свідчить про недостатню підготовку її автора.

Відповіді, які учні знаходять в результаті розв'язання задачі, бажано виділяти: або писати після слова «Відповідь», або підкреслювати. Взагалі розв'язання задачі треба оформляти так, щоб було видно, де його початок, а де кінець. Перевірку розв'язків у таких випадках, коли вона є необхідною складовою частиною розв'язання краще записувати перед відповіддю. В інших випадках її можна записувати після відповіді.

Обов'язково треба вимагати від учнів, щоб усі їх записи в зошитах, у тому числі і розв'язання задач, відповідали вимогам мовного режиму. Зокрема учні повинні додержувати таких правил:

а) залишати поля, робити абзаци;

б) порівняно довгі формули і співвідношення виносити в окремі рядки;

в) при розв'язуванні задач, пов'язаних з величинами, числа треба писати з найменуваннями. Якщо в компонентах дій найменування не ставити, то в результаті його треба брати в дужки. У дужках слід писати і найменування результату ділення на вміщення, наприклад: 90 коп. : 30 коп. = 3 (цукерки).

г) у задачах на складання рівнянь і систем найменування в рівняннях не записують; [2].

Перевірка

Щоб переконатися, що те чи інше розв'язання задачі правильне, звичайно роблять перевірку. Правда, спостереження показують, що найпоширеніший серед учнів критерій правильності розв'язання задачі - відповідь. Розв'язавши задачу, учень звіряє знайдену відповідь з тією, яка є в підручнику, і якщо вони однакові, то робить висновок, що задача розв'язана правильно, а якщо різні, то шукає помилку. У цьому немає нічого поганого; відповіді у підручниках для учнів старших класів значно економлять час, і в цілому їх треба вважати корисними. Але якщо учень знає тільки такий спосіб «перевірки», погано, бо в житті доводиться мати справу в основному з задачами, до яких не дано відповіді. Учень повинен уміти не тільки розв'язувати ті або інші задачі, а й уміти перевіряти їх.

Різні задачі можна перевіряти різними способами.

В одних випадках можна перевірити, чи задовольняє знайдений розв'язок умову задачі, в інших - доводиться складати і розв'язувати задачу, обернену даній, в якій шукане число беруть за дане, а одне з даних - за шукане. Іноді для перевірки доводиться шукати навіть інший спосіб розв'язання.

Перевірку треба робити за умовою задачі, а не підставляти, наприклад, знайдений розв'язок у рівняння, складене за її умовою, бо нерідко допускають помилки саме при складанні рівнянь. Цих помилок подібна перевірка не виявить.

Розрізняють повну перевірку, при якій показують, що знайдений розв'язок задовольняє всі частини умови задачі, і неповну перевірку (контроль), коли перевіряють відповідність знайденого розв'язку тільки деяким (але не всім) частинам умови задачі.

Зрозуміло, що неповна перевірка не дає такої впевненості в правильності розв'язання, як повна. Але іноді, коли повну перевірку виконати важко, роблять неповну.

Досить ефективним слід вважати контроль знайдених загальних розв'язків за допомогою розгляду кількох (найкраще граничних) випадків.

Може також трапитись, що в процесі розв'язування втрачено частину розв'язків. У цьому випадку знайдена відповідь може задовольняти умову задачі, але з цього не випливає, що задачу розв'язано правильно. Перевірка в таких випадках нічого не дасть.

Зауважимо також, що розглянуті способи перевірки можна застосовувати тільки при розв'язуванні задач, коли в результаті дістають розв'язок. Що ж до задач на доведення, то такі способи перевірки до них застосувати не можна.

Найзагальніший і найкращий спосіб перевірки розв'язання задач полягає в уважному повторному аналізі всіх елементів розв'язання.

Чи для кожної задачі учень повинен робити перевірку? Ні, бо це забрало б дуже багато часу. Перевірку треба обов'язково вимагати там, де вона є необхідною складовою частиною розв'язання (наприклад, щоб виявити і відкинути сторонні корені рівняння). У всіх інших випадках, якщо учитель не вимагає, учень може не робити перевірку. В контрольних і екзаменаційних роботах перевірку робити бажано. Але про це учитель повинен повідомити учнів перед виконанням завдання, і не треба дуже детально описувати перевірку. Іноді вчителі вимагають, щоб учні починали перевірку розв'язання задачі на складання рівняння приблизно такими словами: «Перевіримо, чи справді друга бригада виконала завдання на два дні раніше, коли перша виготовляла щодня по 40 деталей, а друга — по 45, причому завдання першій бригаді було дано 400 деталей, а другій на 10% менше...» По суті вони примушують учнів переписувати текст задачі, а потім робити перевірку, інколи більшу, ніж саме розв'язання. Такі багатослівні перевірки вимагати від учнів, тим більше в екзаменаційних роботах, не слід. Перевірку можна не супроводжувати ніякими словами, а тільки записувати дії і перетворення.

Усне розв’язування задач

Не обов'язково всі розв'язування записувати на дошці. Приблизно половину задач у класі доцільно розв'язувати усно. В результаті можна набагато збільшити кількість розв'язаних задач і цим самим сприяти поліпшенню якості знань і навичок учнів.

Розв'язуючи задачу, наприклад на обчислення, учні мають справу з двома такими моментами:

1) із з'ясуванням залежностей між шуканими і даними в задачі значеннями величин;

2) з виконанням обчислень чи перетворень.

Звичайно другий момент становить менше труднощів, бо перед розв'язуванням текстових задач учні розв'язують дуже багато прикладів на обчислення. Із з'ясуванням залежності між величинами справа значно гірша, бо учні дуже мало тренуються в цьому. Якщо ми хочемо, щоб учні добре розв'язували різні текстові задачі, треба, щоб вони більше вправлялися в з'ясуванні залежностей між величинами. Для цього найкраще дати їм спочатку розв'язувати задачі з найпростішими числовими даними, щоб обчислення забирало якнайменше часу і енергії. Такі задачі краще розв'язувати усно.

Наприклад, навіть чотирикласникам для усного розв'язування іноді слід пропонувати такі задачі:

«У Миколки 15 коп., а в Толі — в 3 рази більше. На скільки копійок у Толі більше, ніж у Миколки?»

«За 2 години поїзд проходить 90 км. Скільки він пройде за З години?»

Розв'язування кожної з таких задач потребує менше хвилин; в їх розв'язуванні беруть участь і найслабші учні, а це дає дуже добрі результати.

Усно можна розв'язувати задачі не тільки в молодших та середніх класах, а й у старших. [2; 3; 5; 18].

 

3. Методичні основи навчання учнів алгебраїчному методу розв’язування текстових задач

Вступні зауваження

Задачі є й метою, і засобом навчання та математичного розвитку школярів. З цієї характеристики ми й виходимо, розглядаючи розв'язування задач складанням рівнянь. Роль і призначення таких задач - допомогти учням оволодіти методом рівнянь, який є своєрідною формою аналітичного методу мислення. Адже розв'язуючи задачу за допомогою складання рівняння, ми починаємо міркувати з невідомого - з того, що нам треба знайти, а це характерна ознака застосування аналітичного способу розв'язування.

Програма орієнтує на необхідність засвоєння учнями апарату рівнянь і нерівностей як основного засобу математичного моделювання прикладних задач. Треба мати на увазі, що складання рівнянь чи нерівностей за умовою задачі є прикладом конструювання простішої математичної моделі. Тому задачі виступають як мета навчання.

Необхідність спеціальної роботи з формування в учнів умінь розв'язувати задачі за допомогою рівнянь врахована у побудові діючих підручників для 7—9-х класів, де цьому питанню присвячено окремі пункти (стосовно лінійних рівнянь і їх систем, квадратних і раціональних рівнянь, систем рівнянь другого степеня). [1; 2; 3; 18].

Одночасно в підручниках чітко простежується використання задач як допоміжного засобу для формування нових понять. Наприклад, у 7-му класі за допомогою задачі вводиться поняття про систему рівнянь з двома змінними. [7; 9].

У 8-му класі прикладом такого підходу може бути розгляд задачі, на основі якої вводиться поняття про розв'язування системи нерівностей з однією змінною. [8; 10].

Розв'язування задач складанням рівнянь сприяє кращому засвоєнню учнями понять «рівняння», «корінь рівняння», «система рівнянь», «розв'язок системи рівнянь».

Як показав вивчений досвід, при такій організації роботи частина учнів розв'язують задачі в своїх зошитах самостійно, звіряючи свої відповіді з тими, що на дошці, а частина списує з дошки все розв'язання. У цьому є цінність, бо ті учні, які не зрозуміли пояснень учителя або забули попередній матеріал, списуючи з дошки, вчаться розв'язувати. Але в цьому і недолік такої роботи, бо завжди є такі учні, які при цьому вчаться тільки списувати. Тому розв'язувати задачі лише таким способом недоцільно. Час від часу треба давати задачі і для самостійного розв'язування.

Проте неправильно було б дуже критикувати таке розв'язування задач і вправ біля дошки тільки тому, що частина учнів намагається списувати. Не секрет, що списують ті учні, які не вміють розв'язувати. Самостійна робота їм не допоможе. [1; 2].

Одним з важливих завдань розв'язування задач є активізація пізнавальної діяльності учнів, розвиток у них уміння розмірковувати, співставляти й протиставляти факти, порівнювати розв'язувану задачу з розглянутими раніше, знаходити в них спільне й відмінне. Розв'язування задач складанням рівнянь необхідно використати для формування в учнів уміння давати повноцінну аргументацію висловлених тверджень, виконуваних перетворень виразів, обчислень тощо. Воно повинно сприяти вихованню в учнів таких якостей, як уміння приймати певні незаплановані рішення на основі аналізу ситуацій. Це необхідна риса сучасного працівника будь-якої галузі народного господарства. У повсякденному житті, у виробничій діяльності людям різних професій доводиться розглядати всі можливі випадки ситуації, що склалася. Учням слід це роз'яснювати і підкреслювати важливість такого уміння для вивчення математики. У свою чергу під час розв'язування задач вчитель повинен навчати учнів розглядати всі можливі варіанти заданої в задачі ситуації.

Задачі широко використовуються для створення проблемної ситуації перед вивченням нових математичних фактів, понять і методів. У підручниках з алгебри 7—9-х класів за допомогою задач створюються проблемні ситуації для введення нових видів рівнянь і вивчення способів їх розв'язування. Проте використані з цією метою задачі не завжди можна вважати вдалими, бо створення проблемної ситуації повинно бути пов'язане з подоланням певних труднощів, організацією пошукової діяльності учнів. Якщо ж використовувати з цією метою відомий учням матеріал, то ніякої проблемної ситуації не виникає Кожна розв'язувана задача повинна збагачувати знання і досвід учнів, навчати їх математичної діяльності. Для розвитку уміння розв'язувати задачі важливе значення має актуалізація набутих знань під час розв'язування нових задач. Мова йде про вибір з минулого досвіду потрібних відомостей і методів та використання їх у нових умовах. Але цей процес не відбувається автоматично, прийомів математичної діяльності під час розв'язування задач учнів треба навчати. [3].

Суттєвою вимогою програми в питанні розв'язування задач є диференційований підхід до учнів: рівень складності задач, що пропонується слабшим учням, повинен відповідати вимогам програми; учням, які досягли цього рівня, доцільно давати складніші задачі.

Під час розв'язування задач складанням рівнянь необхідно навчати учнів прийомів перевірки. Найпоширенішим способом перевірки розв'язання задачі є обґрунтування того, що знайдений розв'язок задовольняє умову. Саме умову, а не рівняння, складене за умовою задачі, бо можна неправильно скласти рівняння, а розв'язати його правильно. [1; 2].

Корисно з метою перевірки скласти і розв'язати задачу, в якій шукане число беруть за дане, а одне з даних - за шукане. Але цей спосіб пов'язаний із значними витратами часу, а тому його не можна застосовувати до всіх задач.

У шкільній практиці основною формою розв'язання задач на уроці є колективний аналіз задачі з наступним докладним розв'язуванням її на дошці та в зошитах. Щоб запобігти виключенню з педагогічного процесу частини учнів, які механічно списують готове розв'язання з дошки, необхідно урізноманітнювати види роботи з задачним матеріалом, застосовувати такі методи, які активізують пізнавальну діяльність усіх учнів. Активній самостійній діяльності учня повинно передувати певне наслідування, робота, виконана за вказівками вчителя або учня, який розв'язує задачу на дошці чи коментує вголос її розв'язування з місця. Така допомога потрібна, зокрема, при поясненні способів розв'язування нових видів задач, задач підвищеної складності, при ознайомленні учнів із спеціальними формами запису розв'язання і т. п.

Основним помічником учня є підручник, де подано пояснення щодо розв'язування задач складанням рівнянь і відповідні зразки. Ці зразки за формою є своєрідними алгоритмічними приписами, де в лаконічній формі подано перелік кроків, що ведуть до одержання відповіді. [3; 4].

Вибір основного невідомого

Треба пояснити учням, що в багатьох випадках основне невідоме можна вибирати кількома способами.

Для зміцнення навичок подання допоміжних невідомих через основне невідоме доцільно продовжити тренування учнів у встановленні двобічних зв'язків між величинами, що фігурують в умові задачі: якщо одна величина більша від другої на якесь число (у кілька разів), то друга — менша від першої на це саме число (у стільки ж разів).

З цією метою треба використовувати задачі з підручника. Наприклад, учитель пропонує перефразувати задачу так, щоб замість слова «більше» вживалося слово «менше», а зміст задачі не змінювався. [3].

Задача 1. У трьох цехах заводу працює 1274 робітники. У першому цеху на 70 робітників менше, ніж у другому, а в другому — на 84 робітники менше, ніж у третьому. Скільки робітників працює в кожному цеху?

Позначивши через х число робітників у другому цеху, дістанемо рівняння:

х + (х – 70) + (х + 84) =1274,

х + х – 70 + х + 84 = 1274,

3х + 14 = 1274,

3х = 1260

х = 420.

Доцільно дати учням домашнє завдання за варіантами відносно вибору основного невідомого. Наприклад, за х позначити число робітників другого цеху, а іншому варіанту – число робітників третього цеху.

Завдання перевіряється за заздалегідь підготовленою вчителем таблицею, яку після розбору учні записують у зошити.

І	х	х – 70	х – 84 – 70
ІІ	х + 70	х	х – 84
ІІІ	х + 70 + 84	х + 84	х

Записуються також відповідні рівняння. [3; 17].

Далі з'ясовується питання, яке ж невідоме доцільніше вибрати за основне. Мабуть, учні скажуть, що через х доцільно було позначити кількість робітників ІІ цеху.

Учитель підкреслює, що під час розв'язування задач на поділ числа на нерівні частини у різницевому чи в кратному відношеннях для зручності беруть за основне невідоме найменшу величину (якщо це можливо). Проте це необов'язково.

Дехто може заперечити, що такий докладний аналіз однієї, до того ж нескладної, задачі зайвий. Це хибна думка. Спостереження показують, що типовим недоліком при введенні методу рівнянь для розв'язування задач є поспішність, ігнорування того факту, що частина учнів не усвідомлює матеріалу на належному рівні. Розв'язання однієї задачі кількома способами буває значно корисніше, ніж розв'язання одним способом кількох задач. Після розв'язання задачі кількома способами чи введення якихось нових елементів важливо підводити підсумок проведеної роботи, акцентувати увагу учнів на необхідність засвоєння тих прийомів, які будуть потрібні їм у наступній діяльності.

У процесі розв'язування задач складанням рівнянь необхідно привчати учнів до поетапного самоконтролю і повторного аналізу всіх елементів розв'язування. Ці навички особливо важливі під час розв'язування задач за допомогою системи рівнянь другого степеня, бо тут учні іноді втрачають частину розв'язків. Знайдена ними відповідь може задовольняти умову задачі, але це не означає, що задача розв'язана правильно, бо розглянуто не всі випадки значень шуканих величин.

Зробимо ще одне дуже важливе зауваження. Само по собі рівняння, складене за умовою задачі, не є повною математичною моделлю реальної ситуації, відображеної в умові задачі. Воно не враховує фізичні властивості предметів і явищ, про які йдеться в задачі, реальних співвідношень між допустимими значеннями відповідних фізичних величин. Тому розв'язки рівняння можуть не відповідати дійсності, і треба обов'язково перевірити, чи задовольняють корені рівняння умову задачі, чи враховують змістовні обмеження для значень розглядуваних величин. Отже, відповідь, що дістали за складеним рівнянням, необхідно перевірити за змістом задачі. Для цього досить при значенні невідомого, яке дорівнює кореню рівняння, обчислити по черзі значення величин, що входять у задачу. Якщо значення якоїсь величини виходить за межі допустимого за змістом задачі, то випробуваний корінь не може бути розв'язком задачі. Щоб корінь рівняння був розв'язком задачі, він має задовольняти всім змістовним обмеженням величин, введених у задачу (явно чи неявно).

Основні етапи розв’язування задач методом рівнянь

У задачах, розв'язуваних за допомогою рівнянь, розглядаються найрізноманітніші залежності між різними величинами. Ось чому намагання методистів знайти і дати учням якесь загальне, універсальне правило для складання рівняння за умовою задачі не дали очікуваного результату. Інший підхід полягає в тому, що в розв'язуванні задач методом рівнянь виділяють два етапи, кожний з яких передбачає застосування певних методичних підходів.

Перший етап - складання алгебраїчних виразів на основі залежностей, даних у задачі, другий - складання самого рівняння. Обидва етапи мають свої специфічні труднощі, для подолання яких треба застосовувати особливі прийоми, використовувати додаткові вправи. [3].

Подання залежностей, що фігурують в задачі у вигляді виразів

За діючою програмою з математики учні 5 – 6-х класів набувають певного досвіду складання буквених виразів, що виражають різноманітні залежності між величинами. Ця робота продовжується і в курсі алгебри, зокрема на матеріалі про функцію. Проте, як свідчить практика, набуті учнями навички складання виразів у багатьох випадках недостатні для розв'язування задач, вони потребують корекції і вдосконалення. Виникає необхідність спеціального тренування школярів у складанні буквених виразів, які є типовими для певних груп задач, за допомогою відповідно дібраних вправ.

Найбільшої уваги потребує подання в алгебраїчній формі величини, що знаходиться у даному різницевому або кратному відношенні з другою величиною.

Частина учнів ще і в 7-му класі відчуває труднощі при переведенні на мову алгебри залежностей «на стільки - то більше, менше», «у стільки-то разів більше, менше». З цими учнями необхідно додатково розв'язувати вправи такого, наприклад, змісту:

1. Число х більше від числа 7 на 3. Складіть рівність.

(х—7 = 3; х— 3 = 7; х = 7 + 3).

2. Складіть рівність, якщо а більше від 5 у 4 рази.

3. Сума двох чисел дорівнює 15. Одне з них а. Запишіть друге число.

4. Дано числа х і у. На скільки перше число більше за друге? Друге більше від першого?

5. В одному кошику с яблук, у другому у 2 рази, а в третьому у 4 рази більше, ніж у першому. Скільки яблук у другому кошику, у третьому, у трьох кошиках разом?

6. У п'ятому класі х учнів; у шостому на 3 учні більше, ніж у п'ятому, а в сьомому на 2 учні менше, ніж у шостому. Скільки учнів у сьомому класі?

7. На верхній полиці лежить т книжок, на середній удвоє, а на нижній утроє більше, ніж на верхній. Скільки книжок на усіх трьох полицях?

8. В одному кошику х груш, у другому на 12 груш більше, а в третьому на 25 груш більше, ніж у другому. Скільки груш у всіх трьох кошиках?

Використання подібних вправ для роботи на уроках залежить від рівня підготовки класу в цілому і наявності в ньому учнів, у знаннях яких є істотні прогалини. Відповідно організується фронтальна робота з класом, групова або індивідуальна робота. В окремих випадках виникає необхідність розгляду вправ пропедевтичного характеру в спеціально відведений час на початку або в кінці уроку поза зв'язком їх з основною темою. Найбільший ефект дає диференційована індивідуальна допомога учням, що відчувають труднощі в оволодінні програмним матеріалом.

У 7 - му класі значну питому вагу мають задачі, зміст яких переважно полягає в тому, що даються дві нерівні однорідні величини, які підлягають певним змінам. Складаючи вирази на основі залежностей, даних в умові, учні повинні подати алгебраїчною мовою зміни, яких зазнавали дані величини.

Підготовчими тут можуть бути вправи такого змісту:

1.У двох паралельних класах по х учнів. З одного класу перевели в другий двох учнів. Скільки учнів стало в кожному класі?

2.В одному ящику 20 кг гвіздків, а в другому 30 кг. Скільки кілограмів гвіздків буде в кожному ящику, якщо з другого перекласти в перший х кг?

3.В одній пачці а зошитів, у другій у 2 рази більше. Скільки зошитів буде в кожній пачці, якщо з більшої перекласти в меншу 10 зошитів?

Підготовчі вправи, спрямовані на актуалізацію необхідних знань, мають бути максимально наближені до змісту задач, які розв'язуватимуться в певному розділі.

Розглянемо це питання стосовно до задач з відсотковими розрахунками і відповідно задач з використанням запису числа у вигляді суми розрядних доданків та деяких інших.

Треба нагадати учням, що відсоток - це одна сота частина. Якщо якусь величину позначено через х, то один її відсоток становить 0,01 х, 25 % становлять 0,25х, 130 % — відповідно 1,3х і т. п. Якщо число а збільшили на 45 %, то це записують як 1,45а, якщо число в зменшили на 18 %, то воно становить 0,82 свого попереднього значення, тобто дорівнює 0,82в. Цей останній випадок потребує особливої уваги, бо учні іноді неправильно визначають основне число в задачах з «нарощеним числом».

Проаналізуємо цей помилковий підхід на прикладі задачі, розв'язаної складанням системи двох лінійних рівнянь. [3].

Задача 2. Токар і його учень повинні були виготовити за зміну 90 деталей. Завдяки тому, що токар перевиконав план на 20 %, а учень на 10%, вони виготовили 105 деталей. Скільки деталей виготовляли токар і його учень щодня?

Діючи за шаблоном, деякі учні вибирають за невідомі кількості деталей, які треба знайти, тобто

х — кількість деталей, що їх щоденно виготовляв токар, відповідно

у — кількість деталей, що їх щоденно виготовляв учень.

Далі міркують так: після підвищення продуктивності праці токар став виготовляти щоденно х деталей, отже, спочатку він виготовляв їх на 20 % менше, тобто 0,8х, а учень відповідно 0,9у.

Розв'язуючи систему рівнянь

дістають х = 45, у = 60. Цей розв'язок суперечить здоровому глузду. Правильне розв'язання задачі дістанемо тоді, коли за основні невідомі вибрати «ненарощені числа», тобто кількості деталей, які виготовляв токар і його учень до підвищення продуктивності праці. Розв'язуючи систему рівнянь

дістанемо х = 60, у = 30, тобто х + у=90. Після підвищення продуктивності праці маємо: 1,2х = 72; 1,1у = 33, тобто 1,2х + 1,1у = 105. [3, 17].

Під час розв'язування задач доводиться виконувати допоміжні відсоткові розрахунки з відомими числами: знаходити кілька відсотків від числа, число за його відсотками, обчислювати відсоткове відношення двох чисел. Усі такі розрахунки треба проводити, подаючи відсотки у вигляді дробів.

Розв'язуючи задачі з відсотками в класі або задаючи їх учням для домашньої роботи, учитель повинен щоразу думати про допомогу, яку треба надати учням (вказівку, застереження), щоб запобігти зайвих ускладнень і помилок.

Звернемося до задач, перед розв'язуванням яких учням треба нагадати особливості десяткового запису чисел, подання чисел у вигляді суми розрядних доданків. Щоб скласти рівняння для розв'язування таких задач, учні повинні знати, як зміниться число, якщо до нього дописати нуль, дописати справа одну цифру, дописати до даного числа одну цифру зліва.

Якщо до задуманого числа х дописати справа нуль, то воно збільшиться у 10 раз, тобто дорівнюватиме 10х. Якщо ж до задуманого числа у дописати справа одну цифру, наприклад 5, то його запис буде 10у + 5. Нарешті, якщо до даного трицифрового числа х дописати зліва одну цифру, наприклад 7, то його запис буде мати вигляд 7000 + х. Для розв'язування ряду інших задач треба вміти записати у вигляді суми розрядних доданків двоцифрові, трицифрові і т. д. числа.

Недостатній досвід оперування цими відомостями не дозволяє учням «з ходу» розв'язувати подібні задачі. Треба актуалізувати їх знання про десятковий запис чисел, виконати ряд вправ такого, наприклад, змісту:

1.Скільки одиниць містить число, яке має а десятків і в одиниць? Скільки одиниць буде в числі, яке дістанемо, коли в даному числі переставимо цифри десятків і одиниць?

2.Скільки одиниць у числі, що складається з а сотень, в десятків і с одиниць? Скільки буде одиниць, якщо цифри даного числа напишемо у зворотному порядку?

3.Як зміниться дане число, якщо до нього справа приписати два нулі, цифру 6?

4. На скільки збільшиться дане двоцифрове число, якщо до нього зліва приписати цифру 3? Те саме для трицифрового, чотирицифрового чисел.

Вміщені в кожному розділі задачі мають узгоджуватися з тими теоретичними відомостями, які вивчаються в певний час. Ці вимоги в основному додержані в діючих підручниках, проте труднощі, які відчувають учні під час самостійного розв'язування задач методом рівнянь, переконують в необхідності спеціальної роботи над деякими типовими залежностями, що фігурують в задачах.

Розглянемо для прикладу так звані задачі на рух. Цим задачам відведено значне місце в 3—6-х класах, і учні набувають певного досвіду в їх розв'язуванні.

У підручниках 7—9-х класів задачі на рух представлені у всіх розділах, пов'язаних з розглядом рівнянь, нерівностей та їх систем. Завдання вчителя полягає в тому, щоб озброїти учнів міцними навичками в складанні математичних виразів для залежностей, типових для задач на зустрічний рух, рух у протилежних напрямках і в одному напрямку. Особливої уваги потребує розв'язування задач на рух за допомогою раціональних рівнянь у 8-му класі, бо ці задачі викликають в учнів труднощі. Вкажемо на необхідність певної підготовчої роботи до розв'язування задач на рух, де використовуються поняття «рух за течією», «рух проти течії», «швидкість човна у стоячій воді», «власна швидкість теплохода» тощо.

Учні, спираючись на власний життєвий досвід, без труднощів усвідомлюють відповідні залежності, але їх треба своєчасно розглянути.

Розв'язуючи задачі на рух за допомогою рівнянь у 5—6-х класах, учні набули певного досвіду встановлення залежностей між даними і шуканими величинами в таких задачах. І все ж розв'язування дещо ускладнених задач на рух у курсі алгебри викликає в частини учнів значні труднощі. Тут можуть допомогти настанови, що розкривають ці залежності в загальному вигляді. Слід підкреслити учням, що, формулюючи ці закономірності, ми маємо на увазі «ідеальні умови», за яких здійснюється рух: швидкості рухомих тіл сталі на всьому проміжку шляху, тобто їх рух рівномірний, рух відбувається по прямій, зустріч відбувається в точці тощо. [1; 2; 3;5].

 

4. Формування вмінь розв’язувати текстові задачі на:

4. 1. спільну роботу

Під час вивчення раціональних рівнянь учні зустрінуться з так званими задачами «на спільну роботу» («на обернені величини»). Задачі цього типу звичайно містять відомості про виконання деякими суб’єктами певної роботи, об’єм якої не вказується і не являється шуканим. Припускаємо, що виконувана робота проводиться рівномірно, тобто з однаковою для кожного суб’єкта продуктивністю. Так як величина виконуваної роботи  нас не цікавить, то об’єм всієї роботи приймаємо за одиницю.

Корисно знать стандартну схему розв’язування типових задач.

Нехай один робітник виконає деяку роботу за х годин, та другий - за у годин. Тоді за один час вони виконають відповідно і частин роботи. Разом за одну годину вони виконають + частину роботи. Звідси, якщо вони будуть працювати разом , то вся робота буде виконана за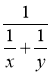

У вирази, які складають для розв'язання цих задач, невідомі входять у знаменники, і для складання рівняння доводиться брати величини, обернені даним у задачі. Учителям відомі труднощі, що виникають в учнів під час розв'язування таких задач. І тут потрібні підготовчі вправи, які б наштовхнули учнів на правильний шлях міркувань.

Доцільно розпочати з розгляду задачі: один учень може зібрати огірки з дослідної ділянки за 20 хв, а другий з цієї самої ділянки може зібрати урожай за 30 хв. За який час вони зберуть огірки з цієї ділянки, працюючи разом?

Як правило, учні називають відповідь 25 хв. Тоді вчитель звертає їх увагу на те, що один учень може виконати цю роботу за коротший час — 20 хв. Чому ж при спільній роботі часу витрачатиметься більше? Так створюється проблемна ситуація, у розв'язанні якої важлива роль належить самому вчителю. Використовуючи при потребі наочні ілюстрації, він пояснює учням, що під час розв'язування задач на спільну роботу треба обов'язково визначати, яка частина роботи виконується за одиницю часу.

Далі учні розв'язують усні вправи такого змісту:

1. Робітник може виконати деяку роботу за 5 год. Яку частину роботи він виконає за 1 год.?

2. Учень може прочитати книжку за а год. Яку частину книжки він прочитає за 1 год.?

3. Один трактор може зорати поле за х днів, а другий на 2 дні швидше. Яку частину роботи виконає другий трактор за один день?

4. Бригада може виконати деяку роботу за у днів. Яку частину роботи вона виконає за 3 дні, за а днів?

5. Робітник може виконати половину (третину, четверту частину) дорученої йому роботи за х днів. За скільки днів він виконає всю роботу, якщо працюватиме з однаковою продуктивністю?

Розв'язуючи задачі на спільну роботу, необхідно ще раз нагадати учням про «ідеальні умови», за яких розглядаються залежності, подані в цих задачах. Зокрема, коли йдеться про спільну дію двох труб чи про спільну роботу двох людей (механізмів), то вважають, що обсяг роботи, яку буде виконано за одиницю часу при заданій пропускній спроможності труб (продуктивності праці), залишається тим самим, незалежно від того, чи труби (робітники, механізми) діятимуть окремо чи разом.

Розв'язуючи з учнями задачі за допомогою рівнянь, учитель може зустрітися і з іншими залежностями між величинами, які або невідомі учням, або недостатньо усвідомлені в попередні роки. У кожному такому випадку необхідно своєчасно реагувати на труднощі, що виникають. [2; 3].

Розглянемо задачу.

Задача 1. Один завод мав виготовити 720 верстатів, а другий за той самий строк – 660 верстатів. Перший завод, виготовляючи щодня на 10 верстатів більше від другого, виконав замовлення на два дні раніше строку, а другий завод, виготовивши 22 верстати понад план, закінчив роботу на один день раніше строку. Скільки верстатів виготовляв щодня кожний завод?

Розв’язання

Позначимо через х кількість верстатів, що їх щодня виготовляв другий завод. Тоді, за умовою задачі, кількість верстатів, які виготовляв щоденно перший завод, буде (х + 10). За цих умов перший завод виконав замовлення за днів, а другий завод працював днів (660 + 22 = 682). Перший завод виконав замовлення на 2 дні раніше строку, тобто робота була розрахована на ( + 2) дні. Другий завод закінчив роботу на один день раніше строку, тобто робота була розрахована на (+1) днів. Для обох заводів був встановлений однаковий строк виконання замовлення, отже, маємо рівняння:

+ 2 = +1,

-   + 1 = 0,

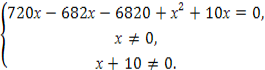
х² + 48х – 6820 = 0,

х₁ = 62, х₂ = -110.

Другий корінь не задовольняє умову задачі. Отже, х = 62, тобто другий завод щодня виготовляв 62 верстати. Перший завод щоденно виготовляв 62 + 10 = 72 (верстати).

Відповідь: 72 верстати, 62 верстати. [17].

4. 2. рух

Зустрічний рух

1) якщо два тіла рухаються назустріч одне одному з двох пунктів, то до зустрічі вони разом проходять усю відстань між цими пунктами;

2) при одночасному виході тіл з двох пунктів час їх руху до моменту зустрічі однаковий для обох тіл;

3) за одиницю часу рухомі тіла зближаються на відстань, що дорівнює сумі їх швидкостей (з розрахунку на цю саму одиницю часу).

Рух в одному напрямку

1) одне рухоме тіло може догнати друге лише тоді, коли швидкість його більша за швидкість тіла, яке рухається попереду:

2) якщо два тіла, відокремлені певною відстанню, рухаються в одному напрямку, ця відстань з кожною годиною (хвилиною, секундою) зменшується і перетворюється в нуль, коли тіло з більшою швидкістю доганяє тіло, яке має меншу швидкість. Зменшення відстані між тілами за одиницю часу дорівнює різниці швидкостей тіл;

3) при одночасному виході з одного й того самого пункту й рухові в одному напрямку тіл, що мають неоднакову швидкість, відстань між ними з кожною годиною (хвилиною, секундою) збільшується. Збільшення відстані між рухомими тілами за одиницю часу дорівнює різниці їх швидкостей;

4) одне тіло дожене або випередить друге за стільки годин (хвилин, секунд), скільки разів різниця між швидкостями цих тіл міститься у відстані, що їх розділяє.

Ці залежності стануть зрозумілішими учням, якщо вдатися до графічних ілюстрацій, які виготовляють самі школярі з допомогою вчителя.

У задачах на рух в більшості випадків рухаються : два тіла назустріч один одному, два тіла в одному напрямі, одне тіло за і проти течії річки, два тіла по колу. [3].

Задача 1. Швидкий потяг за розкладом повинен був пройти залізничний перегін АВ без зупинки за 4 год. Але на відстані 150 км від А його затримали на 20 хв. Щоб прибути на станцію В за розкладом, потяг пройшов решту шляху з швидкістю на 15 км/год. більшою, ніж початкова. Знайти довжину перегону АВ.

Розв’язання

Нехай х км – довжина перегону. Тоді швидкість потяга за розкладом км/год, а після зупинки він рухався із швидкістю ( + 15) км/год. Отже, до зупинки він рухався 150 : = (год.), а після зупинки –

 

З урахуванням часу, затраченого на зупинку, потяг пройшов залізничний перегін за ( + + ) (год.), що за умовою дорівнює 4. Складемо рівняння:

+ + = 4,

Розв’яжемо його:

+ - = 0,

3(600х + 36000 + 4х² – 600х) – 11х² – 660х = 0,

х² – 660х + 108000 = 0,

х₁ = 300, х₂ = 360.

Перевірка показує, що обидва корені рівняння задовольняють умову задачі.

Відповідь: 300 км або 360 км. [17].

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновки

У даній магістерській роботі запропоновано методику навчання учнів алгебраїчному методу розв’язування текстових задач в основній школі, яка реалізується у три етапи: підготовка, ознайомлення і формування відповідних умінь. Під час підготовчої роботи до введення текстової задачі формуємо у школярів уміння порівнювати задачі, аналізувати умову, шукати способи розв’язання задачі; ознайомлюючи дітей з текстовими задачами, вчимо розв’язувати задачі аналітичним способом і розкладати складені задачі на прості; формуючи уміння і навички розв’язування текстових задач, ми продовжуємо вчити дітей розв’язувати задачі аналітичним способом та розкладати складені задачі на прості, на підставі чого складати план розв’язування, формувати уміння порівнювати задачі, а також узагальнюємо структуру однотипових задач.

Під час введення даної теми розвиваємо варіативність мислення учнів, його гнучкість та глибину, свідомість розумових процесів школярів за допомогою спеціальних завдань. Звертаємо увагу на постановку запитання до даної умови; складання задач; розв’язування задач з зайвими даними чи недостатньою кількістю числових даних; на порівняння подібних задач; узагальнення структур задач.

У даній магістерській роботі вивчалися історичні аспекти підвищення продуктивності навчання учнів розв’язувати текстові задачі на уроках алгебри в основній школі. Як ми побачили, що навчити учнів розв’язувати текстові задачі не так то вже і просто. Виходячи з думки вчених, вчителів можна говорити про те, що у методиці навчання учнів розв’язувати текстові задачі не може бути єдиного і конкретного зразка для пояснення матеріалу. Це зумовлено, насамперед, розумовими здібностями учнів і не до кінця сформованими вміннями та навичками при розв’язуванні простих задач.

Методика може запропонувати лише певні види вправ і запитань, які доцільно проводити перед вивченням текстових задач, а кожен вчитель має можливість встановити свій порядок у їх виборі.

У напрямку удосконалення шляхів навчання учнів розв’язувати текстові задачі в школі працює багато вчених. Теоретичний матеріал, який нам подано у методиці навчання математики широко розкриває всі питання, і конкретно пояснює той чи інший вид роботи над задачами.

Для ефективного розв’язування текстових задач ще у початкових класах потрібно прививати любов і цікавість до математики і зокрема до задач. Але як свідчить практика, більшість дітей не просто не вміють розв’язувати задачі, а й не люблять. А цю нелюбов можна пояснити декількома факторами: добір учнів у класі, ставлення батьків до навчання своїх дітей, досвід учителя, неправильне перше ознайомлення із задачею, відсутність диференційованого підходу в навчанні дітей розв’язувати задачі, недостатня робота над її змістом, а ще тим, що вчитель на уроці “женеться” за кількістю розв’язаних завдань і не зважає на потреби і бажання дітей. Психологія нам каже, що учень хоче творити, а творити може кожен. Як же бути з уроками математики? Тут простим запевненням “ти це зможеш” не допомогти. Деяким дітям особливо важко дається розв’язання задач. І знову: що робити? Чому школярі не люблять розв’язувати задачі? Тому що не вміють. Як же навчити учнів не тільки розв’язувати текстові задачі, а ще й викликати інтерес до них? Тут доцільно, при розв’язуванні задач, давати дітям запитання, які б розкривали зміст задачі, ставили додаткові запитання до задачі. Можна запропонувати безліч різних завдань, аби у дітей виникла цікавість до математики. У підручниках з алгебри чітко визначено, чого саме повинні навчити дітей, але в них не можна передбачити необхідну кількість тренувальних вправ для кожного конкретного класу. Тому цю проблему, виходячи з необхідності, має вирішувати сам учитель. Тому доцільно спочатку подати деякі вправи з підручника, для вивчення розв’язування задач певного виду, а потім потрібно використовувати додаткові джерела.

На сьогоднішній день широкого застосування набувають інтегровані уроки, а також інтегровані завдання на уроках. Урок з алгебри теж не є винятком. Доцільно розв’язувати з учнями задачі, які містять тексти, пов’язані з географією, історією.

Нами підібрана добірка завдань для підвищення ефективності методики формування вмінь розв’язувати текстові задачі. Мета формуючого експерименту полягала у перевірці даної добірки завдань для формування у середніх школярів загального вміння розв’язування текстових задач шляхом порівняльного аналізу результатів виконання контрольної роботи у контрольному і експериментальному класах, цілеспрямованих педагогічних спостережень у класах, де проводилося дослідне навчання. Досвід показує, що учні з великим інтересом розв’язують текстові задачі, виявляють кмітливість і творчу самостійність. Також одним із важливих засобів організації цілеспрямованої і систематичної роботи щодо розвитку учнів є різні задачі з логічним навантаженням. Виконуючи їх, учні оволодівають новими знаннями, прийомами розумової діяльності, закріплюють та вдосконалюють вміння та навички.

Отже, всі ці та інші види роботи на уроці алгебри, можна вирішити одне з найголовніших завдань, яке стоїть сьогодні перед учителем на цьому етапі навчання – це навчити учнів розв’язувати текстові задачі.

 

Список використаних джерел

1. Слєпкань З. І. Методика навчання математики: підручник. – 2-ге вид., доповн. і переробл. / З. І. Слєпкань. – К. : Вища шк., 2006. – 582 с.

2. Бевз Г. П. Методика викладання математики: посібник. – вид. 2-ге, переробл. і доповн. / Г. П. Бевз. – К. : Вища шк., 1977. – 376 с.

3. Дубинчук О. С. Методика викладання алгебри 7 – 9 класах: посібник для вчителя. / О. С. Дубинчук, Ю. І. Мальований, Н. П. Дичек. – К. : Рад. шк.., 1991. – 254 с.

4. Власенко О. І. Методика викладання математики. Загальні питання: навч. посібник. / О. І. Власенко. – К. : Вища шк., 1974. – 208 с.

5. Фридман Л. М. Как научиться решать задачи. Пособие для учащихся. 2-е изд., перераб. і доп. / Л. М. Фридман, Е. Н. Турецкий. – М. : Просвещение, 1984. – 175 с.

6. Бевз. Г. П. Алгебра: підруч. для 9 кл. загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз. – К. : Зодіак-ЕКО, 2009. – 288 с.

7. Бевз Г. П. Алгебра: підруч. для 7 кл. загальноовіт. навч. закл. / Г. П. Бевз, В. Г. Бевз. – К. : Зодіак-ЕКО, 2007. – 224 с.

8. Бевз Г. П. Алгебра: підруч. для 8 кл. загальноовіт. навч. закл. / Г. П. Бевз, В. Г. Бевз. – К. : Зодіак-ЕКО, 2008. – 288 с.

9. Кравчук В. Алгебра: підруч. для 7 кл. загальноовіт. навч. закл / В. Кравчук, М. Підручна, Г. Янченко. – Тернопіль, 2005. – 223 с.

10. Кравчук В. Алгебра: підруч. для 8 кл. загальноовіт. навч. закл / В. Кравчук, М. Підручна, Г. Янченко. – Тернопіль, 2005. – 228 с.

11. Математика. Програма для класів з поглибленим вивченням математики 8 – 11 класи. / К., 2001. – 64 с.

12. Математика. Програма для загальноосвітніх навчальних закладів 5 -12 класи. / К. : Ірпінь, 2005. – 64 с.

13. Глущенко Л. Задачі на відсотки / Любов Глущенко // Математика. – К. : пед. преса, 2008, №23 (467). – С. 5 – 9.

14. Вигівська Л. Розв’язування задач за допомогою рівнянь. Алгебра, 7 клас / Л. Вигівська // Математика. – К. : пед. преса, 2006, №16 (364). – С. 3– 5.

15. Костевська Л. Задачі на спільну роботу. Алгебра, 8 клас / Л. Костевська // Математика. – К. : пед. преса, 2005, №10 (310). – С. 14 - 15.

16. Глущенко Л. Розв′язування текстових задач / Любов Глущенко // Математика. – К. : пед. преса, 2008, №31 - 32 (475 - 476). – С. 22 – 48.

17. Бурда М. І. Збірник завдань для державної підсумкової атестації з математики, 9 клас / М. І. Бурда, О. П. Вашуленко. Н. С. Прокопенко. – Х. : Гімназія, 2010. – 256 с.

18. Бевз Г. П. Методика викладання математики. Випуск 8 / Г. П. Бевз, А. С. Білий. – К. : Вид. Рад. шк., 1972. – 208 с.

19. Яценко С. Є. Аналіз стану проблеми особистісно зорієнтованого навчання у психолого-педагогічній літературі / С. Є. Яценко, Л.В. Спусканюк Науковий часопис НПУ імені М. П. Драгоманова. Серія №3. Фізика і математика у вищій і середній школі: 3б. наукових праць – К. : НПУ імені М. П. Драгоманова, 2005. - №5 (12). – С. 45 – 50.