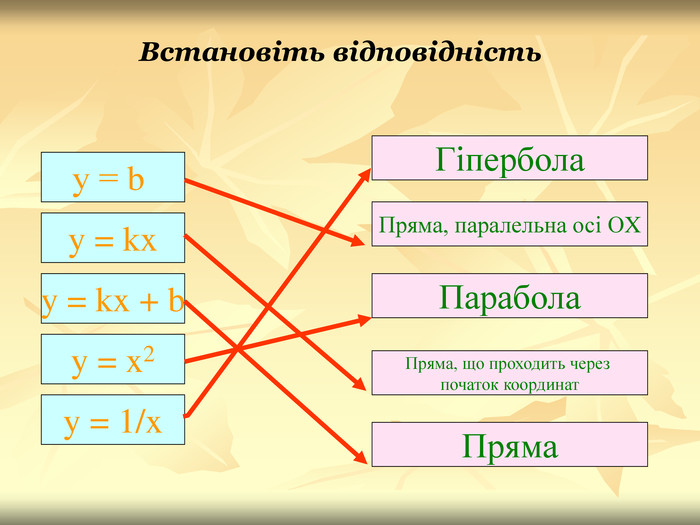
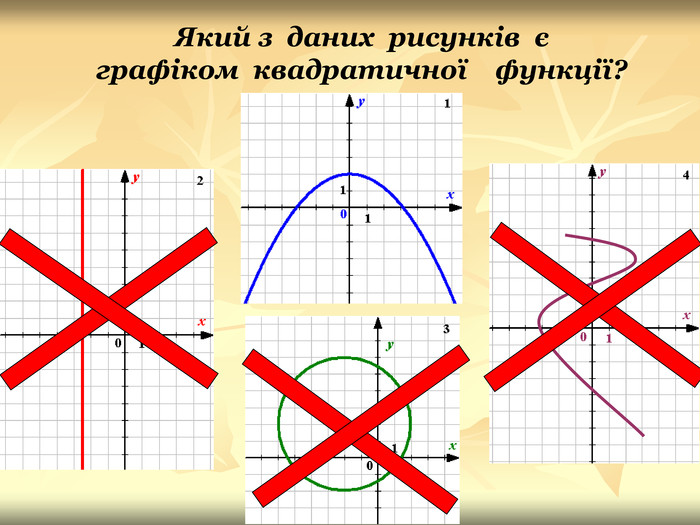
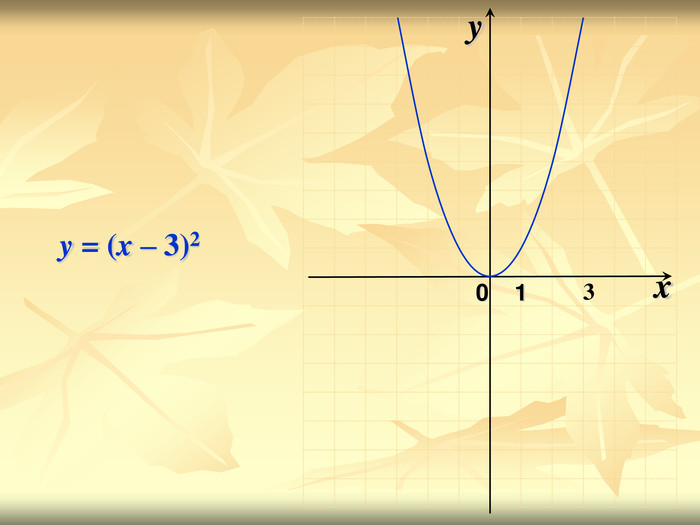
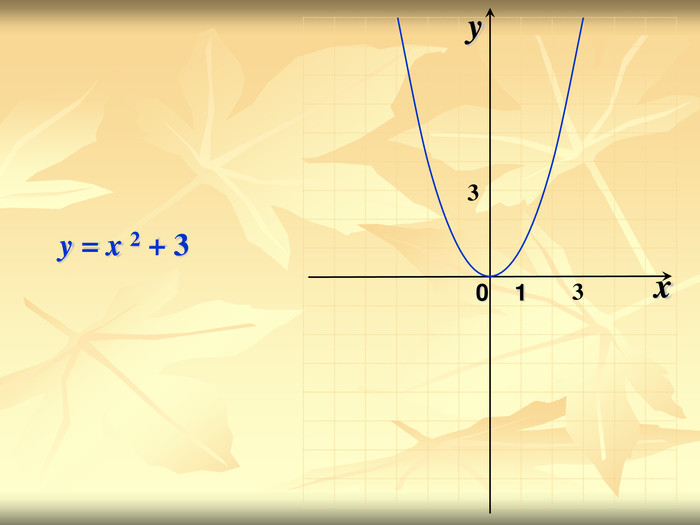
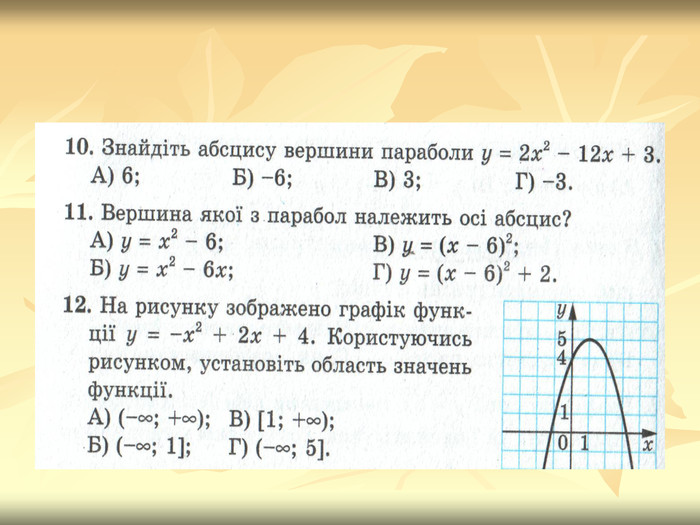
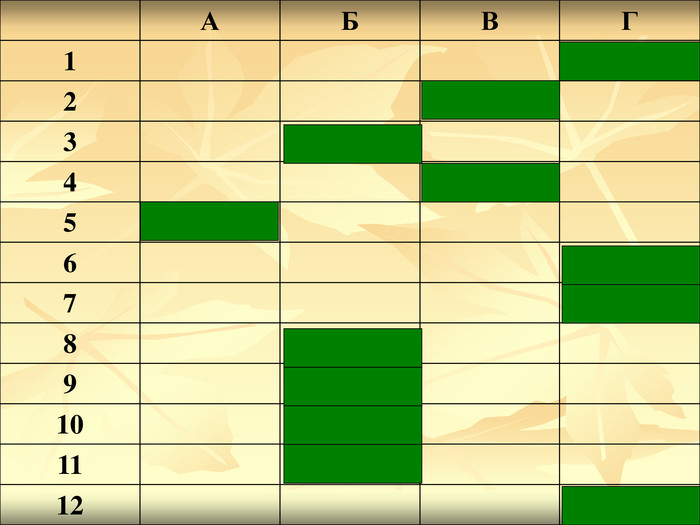
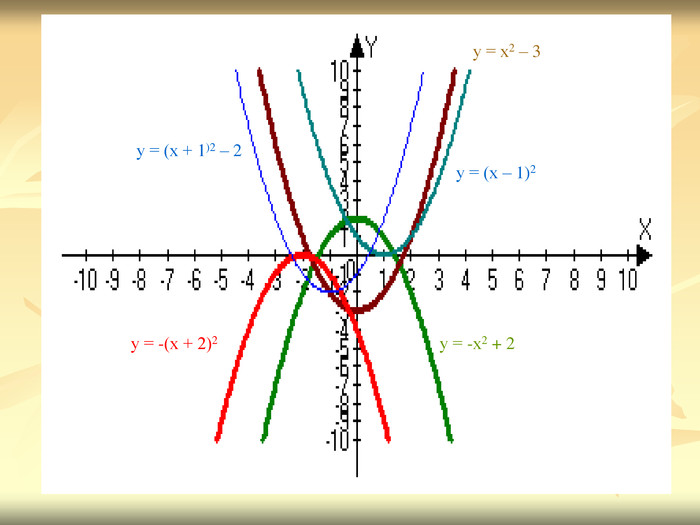
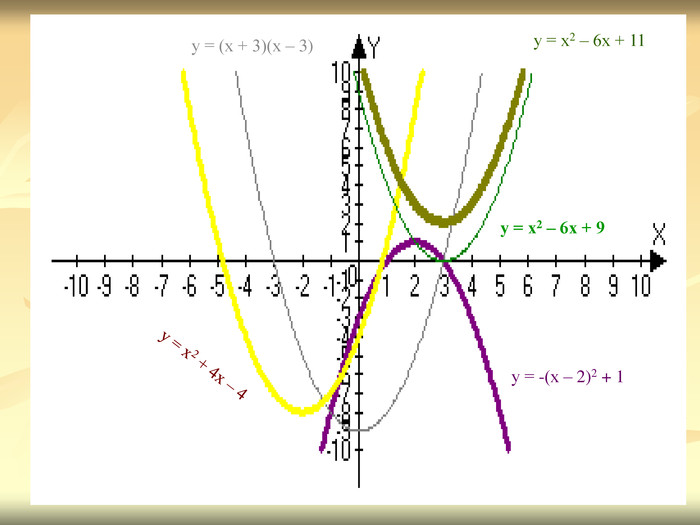
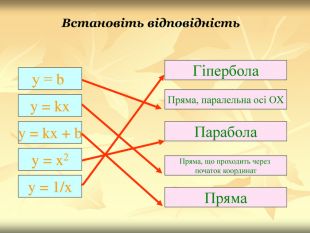
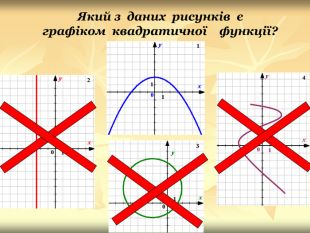
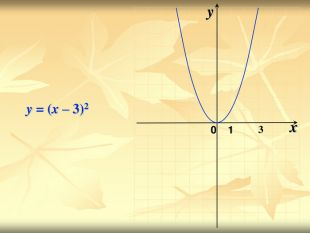
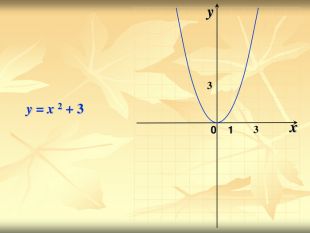
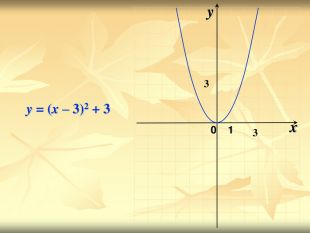
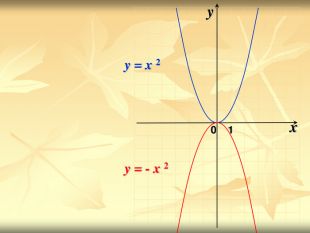
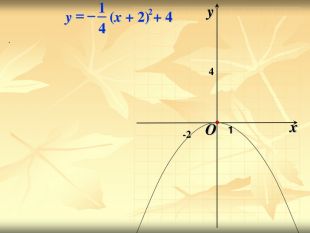
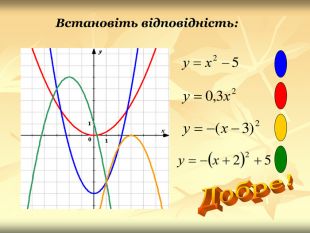
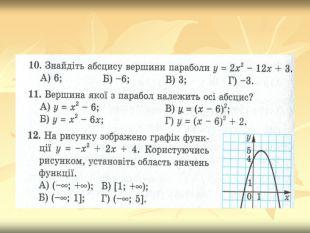
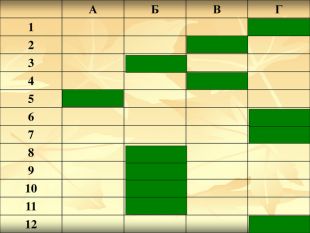
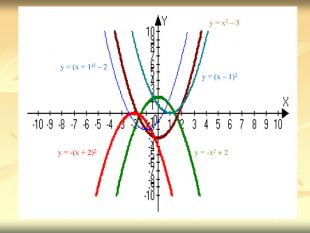
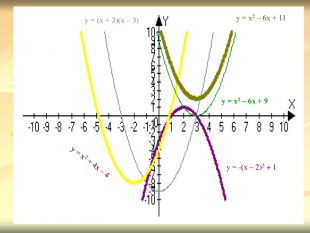
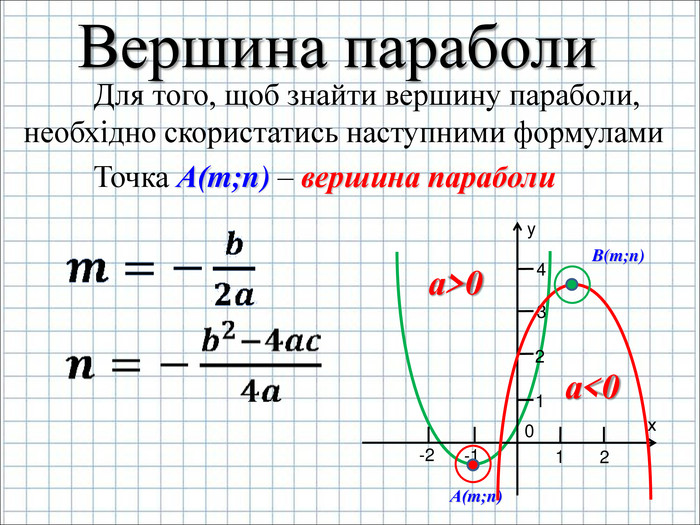
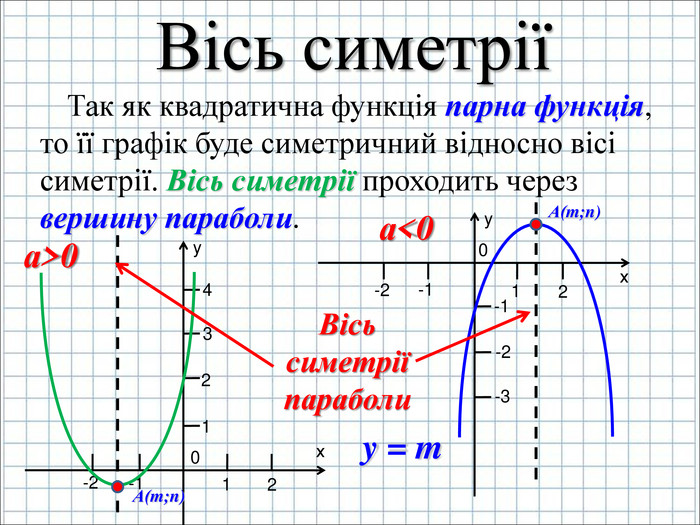
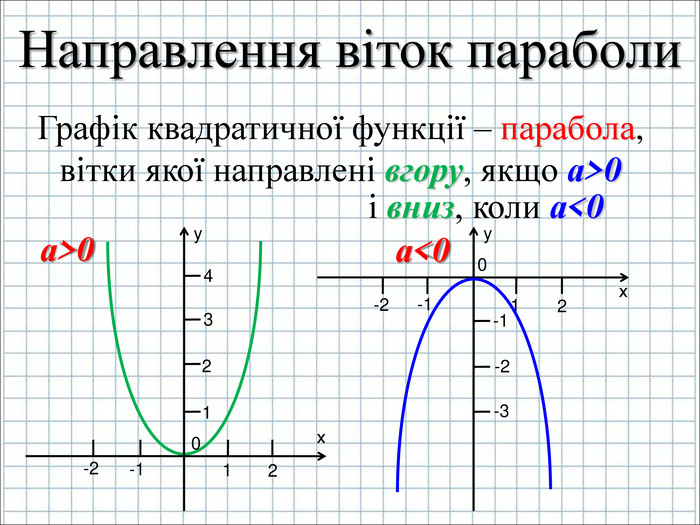
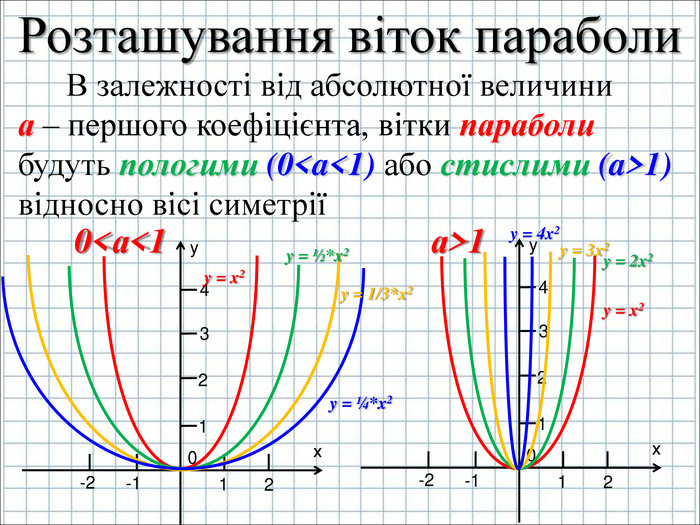
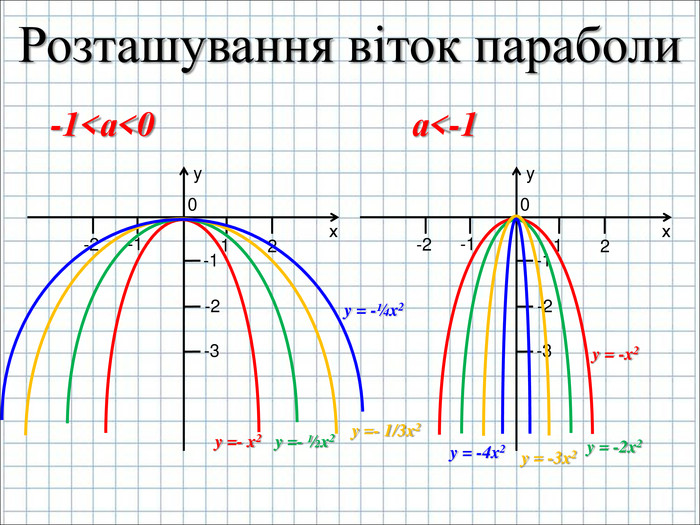
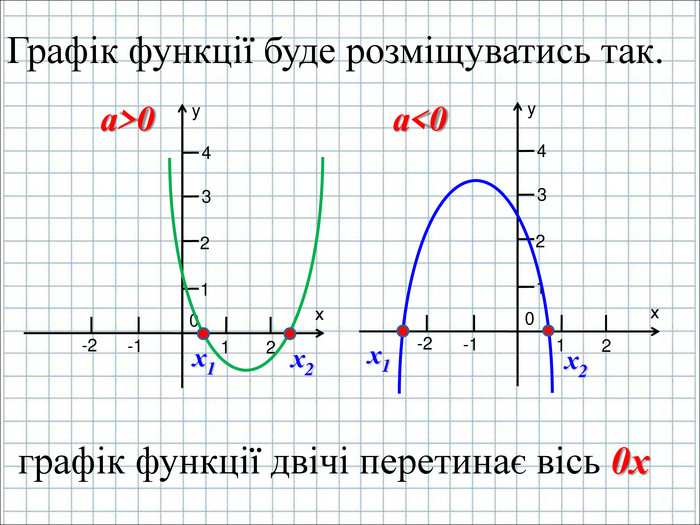
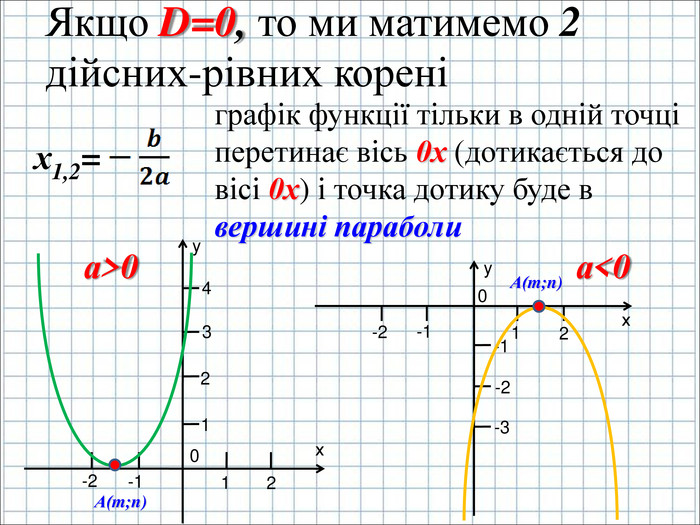
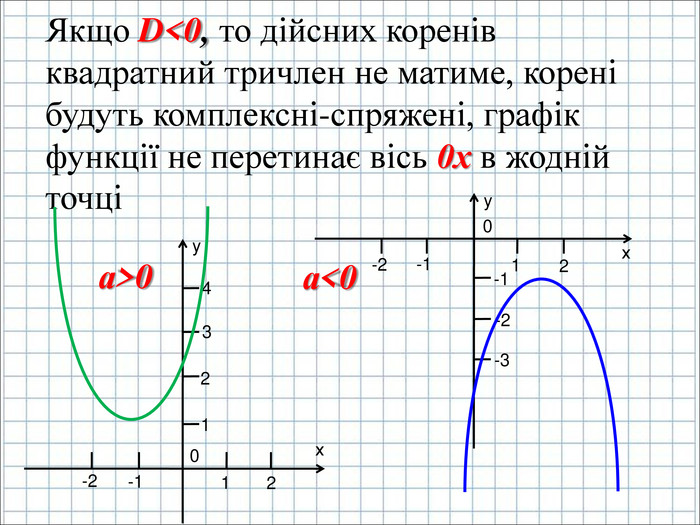
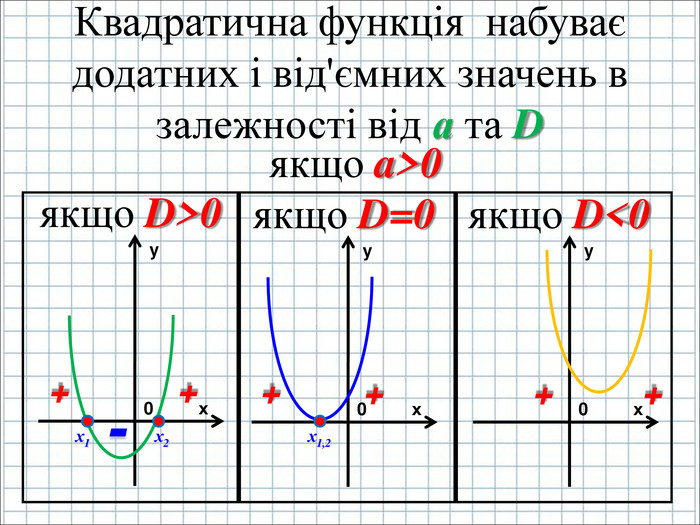
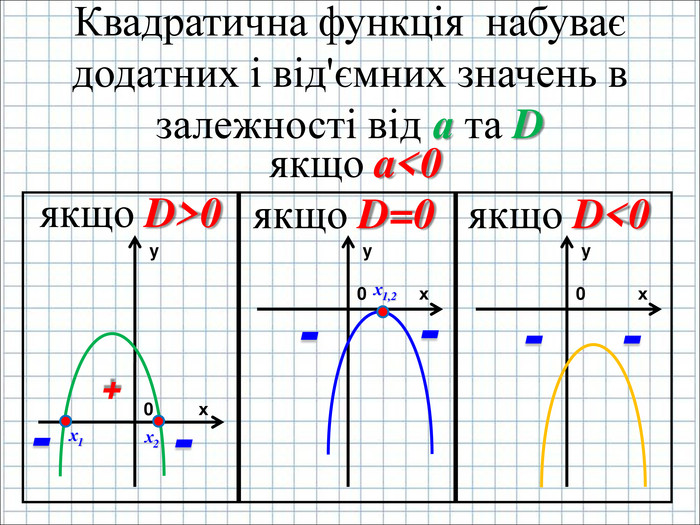
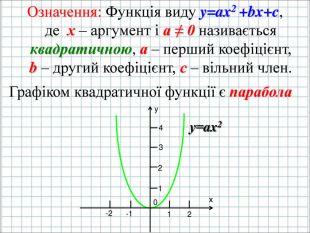
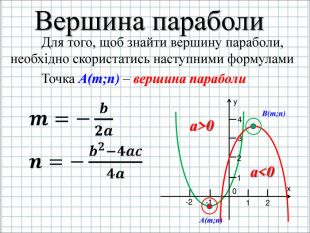
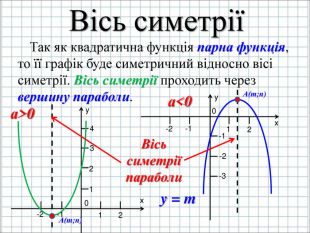
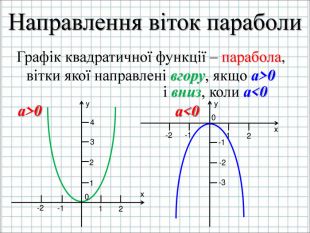
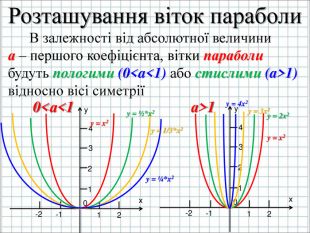
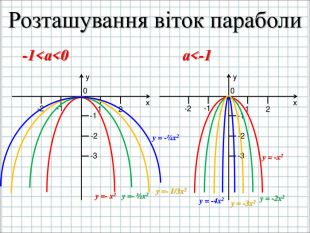
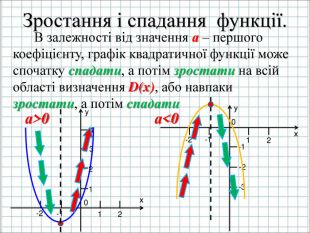
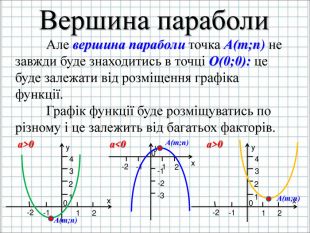
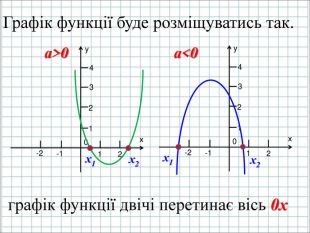
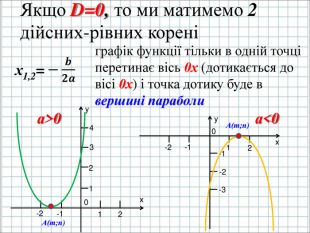
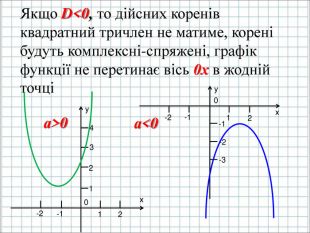
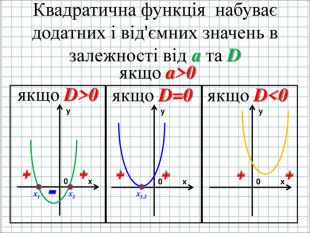
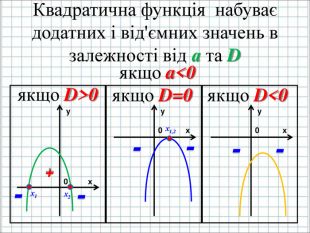
Урок подорож "Квадратична функція"
Дана розробка містить матеріал для проведення уроку за технологією проектного навчання, який побудований як урок подорож країною «Квадратична функція». - урок узагальнення та систематизації з використанням ІКТ та ППЗ Microsoft Excel, Advanced Grapher. Урок побудований так, що учні крокуючи різними станціями, не тільки узагальнюють, систематизують знання з даної теми, удосконалюють практичні навички, а найважливіше пізнають цікавинки де можна зустрітись з параболою у повсякденному житті.
- .doc doc
- »áαáí«½Ñ.WMV.mp4 mp4
- .doc doc
- уроку.ppt ppt
- Показати всі файли
Найвище призначення математики полягає в тому,
щоб знаходити потаємний порядок у хаосі, який нас оточує
Роберт Вінер
Графік – це лінія,
що говорить, яка може багато про що розповісти
М.Б.Балк







Найвище призначення математики полягає в тому,
щоб знаходити потаємний порядок у хаосі, який нас оточує
Роберт Вінер
Графік – це лінія,
що говорить, яка може багато про що розповісти
М.Б.Балк








 _________________________________________________________________________________________________________________________________
_________________________________________________________________________________________________________________________________


про публікацію авторської розробки
Додати розробку




















![7) Область визначення квадратичної функції - ... 8) Область значень функції y=x2: якщо а > 0 , то ... якщо a < 0 , то ... (-∞; +∞) [0; +∞) (-∞; 0] 7) Область визначення квадратичної функції - ... 8) Область значень функції y=x2: якщо а > 0 , то ... якщо a < 0 , то ... (-∞; +∞) [0; +∞) (-∞; 0]](/uploads/files/38078/39026/40324_images/20.jpg)