Найбільше і найменше значення функції

ТЕМА. Найбільше і найменше значення функції на проміжку. Виконаємо разом (на повторення)№1. Знайти екстремуми функції: Розв’язання: D(g): x2+6x+8≠0;x≠-4; x≠-2; g’(x)= 0; 2x+6=0;x=-3;x≠-4; x≠-2; +–+max–-4-2х-3xmax=-3gmax=-1

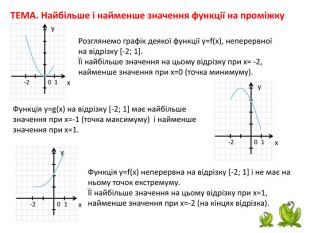
ТЕМА. Найбільше і найменше значення функції на проміжку. Розглянемо графік деякої функції у=f(x), неперервної на відрізку [-2; 1].Її найбільше значення на цьому відрізку при х= -2,найменше значення при х=0 (точка минимуму).ух01-2ух01-2 Функція у=g(x) на відрізку [-2; 1] має найбільше значення при х=-1 (точка максимуму) і найменше значення при х=1.ух01-2 Функція у=f(x) неперервна на відрізку [-2; 1] і не має на ньому точок екстремуму.Її найбільше значення на цьому відрізку при х=1,найменше значення при х=-2 (на кінцях відрізка).

ТЕМА. Найбільше і найменше значення функції на проміжку. Для знаходження найбільшого і найменшого значень функції f(x) на заданому проміжку, треба:перевірити, що проміжок належить області визначення функції;2) знайти похідну функції;3) знайти критичні точки функції;4) вибрати ті критичні точки, що належать заданому проміжку;5) обчислити значення функції у вибраних критичних точках та на кінцях відрізку;6) вибрати серед одержаних значень найбільше і найменше.

ТЕМА. Найбільше і найменше значення функції на проміжку. Приклад 1. Знайти найбільше і найменше значення функції f(x)=2х3-3х2-12х+1 на проміжку [0; 3]. D(f)=R; [0; 3]R;f’(x)= 0;f’(x)= 6х2-6х-12;6х2-6х-12=0;х=-1, x=2 – критичні точки;х2-х-2=0;-1[0;3], 2[0;3], тоді знаходимо значення функції f(x) в точці х=2 і на кінцях відрізка х=0 і х=3f(2)=-19;f(0)=1;f(3)=-8;Відповідь: max f(x) =f(0)=1; min f(x)=f(2)=-19.- найбільше значення- найменше значення[0; 3][0; 3]

ТЕМА. Найбільше і найменше значення функції на проміжку. Приклад 2. Знайти найбільше і найменше значення функції f(x)=х4-2х2+5 , [-1; 3]. D(f)=R; [-1; 3]R;f’(x)= 0;f’(x)= 4х3-4х;4х3-4х=0;x=0, х=-1, x=1 – критичні точки;4x(х2-1)=0;-1[-1;3], 0[-1;3], 1[-1;3] тоді знаходимо значення функції f(x) в точках х=0, х=-1, х=1, х=3f(-1)=4;f(0)=5f(1)=4;Відповідь: max f(x) =f(3)=68; min f(x)=f(-1)=f(1)=4.- найбільше значення- найменше значення[-1; 3][-1; 3]f(3)=68;- найменше значення

ТЕМА. Найбільше і найменше значення функції на проміжку. Приклад 3. Знайти область значень функції у=х3-9х2-7, якщо х[0; 10]. D(у)=R; [0; 10]R;у’(x)= 0;у’(х)= 3х2-18х;3х2-18х=0;х=0, x=6 – критичні точки;3х(х-6)=0;0[0;10], 6[0;10]у(0)=-7;у(6)=-115;у(10)=93;Відповідь: область значень функції [-115; 93].- найбільше значення- найменше значення. Знайдемо значення функції на кінцях проміжку [0; 10] і в критичній точці х=6

Розв’язання. Позначимо через х (у м) довжину однієї з двох сторін паркана, тоді Р=2х+а=80, друга сторона буде а=80-2х, причому 0

Розв’язання. Позначимо через х (у м) довжину однієї з двох сторін прямокутника, тоді Р=2(х+а)=100, х+а=50; друга сторона буде 50-х (м), 0

Розв’язання. Нехай І доданок буде х , тоді ІІ доданок буде 100-х, 0

Список використаної літератури: Математика. Підручник. 10 клас (рівень стандарту). Авт. Істер О. С. Математика. Підручник. 10 клас (рівень стандарту). Авт. Нелін Є. П. Математика. Підручник. 10 клас (рівень стандарту). Авт. Мерзляк А. Г. Математика. Підручник. 10 клас (рівень стандарту). Авт. Бевз Г. П.