Знаходження похідної функції

Тест 10 клас.

Диференціювання функцій

1. Знайти похідну у = х⁵ + 7

А. у’ = х⁴ + 7

Б. у’ = х⁵

В. у’ = 5х⁴

Г. у’ = 5х⁴ + 7

2. Знайти похідну у = cos 6x

А. у’ = sin 6х

Б. у' = -6 sin 6х

В. у' = -6 sin х

Г. у' = - sin 6х

3. Знайти похідну y = sin³ x

А. у' = 3sin² x cos x;

Б. у' = 3sin² x;

В. у' = sin² x cos x;

Г. у' = 3 cos x;

4. Знайти похідну у = sin (3х + 5) і правильне розв’язання

А. у' = (sin(3x + 5))' = cos (3х + 5) · (3x· + 5)' = 3 cos(3x + 5);

Б. у' = sin(3x + 5)' = sin (3х + 5) · (3x· + 5)' = 3 sin (3x + 5);

В. у' = (sin(3x + 5))' = cos (3х + 5);

Г. у' = (sin(3x + 5))' = - cos (3х + 5) + 3;

5. Знайти похідну у = cos²x і правильне розв’язання

А. у’ = (cos² x)' = 2 cos x· (cos x)' = 2 cos x · (- sin x) = = -2 cos x sin x = - sin 2x;

Б. у’ = cos² x' = 2  (cos x)' = 2  · (- sin x) = = -2 sin x ;

В. у’ = (cos² x)' = 2 cos x·cos x' = 2 cos x · sin x = = 2 cos x sin x;

Г. у’ = (cos² x)' = 2· (cos x)' = 2 · (- sin x) = = -2 sin x;

6. Знайти похідну y = cos x²

А. y’ = - sin x².

Б.  y’ = -2 sin x².

В. y’ = -2x sin x².

7. Знайти похідну  у = (3х + 2)⁵⁰

А. y’ = 50 (3х + 2)⁴⁹

Б. y’ = 50 (3х)⁴⁹

В.  у' = 150 · (3х + 2)⁴⁹

8. Знайти похідну у = 

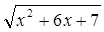
А. y’ = -1/2 (2х + 6)

Б.

В.   

Г.  y’ = ½ (х²+6х+7)