Початкові відомості про похідну функції

Похідна функції, її геометричний та фізичний зміст

Тест

1. Яка з задач призводить до поняття похідної?

А. На масу;  Б. На вартість    В. На швидкість  Г. На результат тренування

2. Приростом функції ∆f називається

А. f(х₀ + ∆x) – f(х₀) Б. f(х₀ + ∆x) + f(х₀) В. ∆х = х - х₀ Г. f(x) – f(х₀)

3. Дотичною до графіка функції F(x) у точці з абсцисою х₀ називається

А. пряма що дотикається до графіка

Б. положення прямої до графіка даної функції, що проходить через одну точку графіка, яка має абсцису х₀.

В. пряма що проходить через дві точки графіка

Г. граничне положення січної до графіка даної функції, що проходить через дві точки графіка, одна з яких має абсцису х₀, якщо різниця абсцис цих точок прямує до нуля.

4. 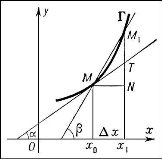Під яким кутом зображено дотичну до графіка функції?

А. 45⁰  Б. 30⁰  В. α  Г. β

5. Знайдіть приріст функції f(x) = x – 1, якщо х₀ = 1, ∆х = 0,1.

А. -0,1;  Б. 0,1;  В. -0,9;  Г. 0,9;

6. Знайдіть приріст функції f(x) = 2х + 3 на відрізку [0; 0.5].

А. -2;  Б. 2;  В. 1;  Г. -1

7. Знайдіть приріст функції f(x) = - 2х + 3  на відрізку [0; 0.5]

А. -2;  Б. 2;  В. 1;  Г. -1

8. Границя (якщо вона існує) відношення приросту функції у точці х₀ до приросту аргументу ∆x, якщо приріст аргументу прямує до нуля називають

А. похідна  Б. монотонність В. Дотична Г. екстремум

9. Знайдіть похідну функції у = х⁶ + 2х⁵ + 5

А. 5  Б. 2х + 5 В. 6х⁵ + 5х⁴ + 5  Г. 6х⁵ + 10х⁴

10. Знайдіть значення похідної функції f(x) = 2 / (x – 1) в точці х = -1

А. – 0,5  Б. 0,5  В. 1   Г. – 1