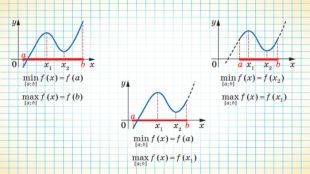
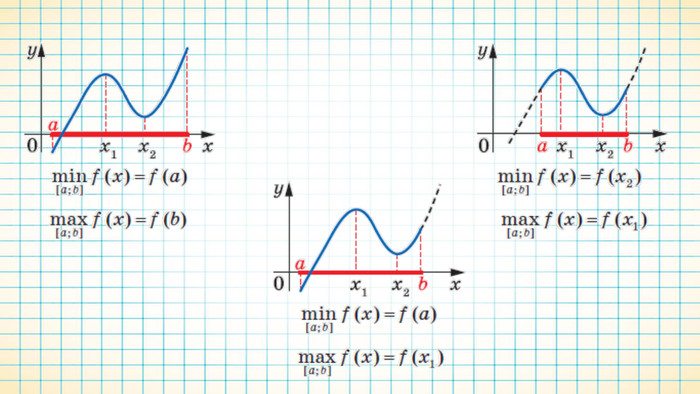
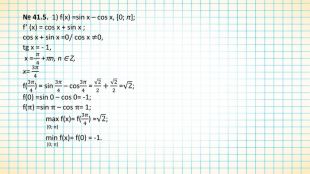Найбільше та найменше значення функції

Матеріали уроку «Найбільше та найменше значення функції на відрізку», 10 клас, профільний рівень» (А. Мерзляк, Д. Номіровський, В. Полонський, М. Якір), п. 41 Н. В. Франчук, Новоград-Волинська загальноосвітня школа І-ІІІ ступенів №5 Житомирської області2020

Найбільше та найменше значення функції на відрізку15.05.2020

Знайти найбільше та найменше значення функції на вказаному відрізку№ 41.1. 1) f(x) =3x2 – x3, [-1; 3]; f’ (x) =6x – 3x2;6x – 3x2 =0;3x(2 –x) =0;x=0 або x=2f(-1) =3∙(-1)2 –(-1)3=4;f(0) =3∙02 -03=0;f(2) =3∙22 -23=4;f(3) =3∙32 -33=0;max f(x)= f(-1) = f(2) =4; [-1; 3]min f(x)= f(0) = f(3) =0.[-1; 3]4) f(x) =x2 +8𝑥−1, [-3; 0];f’ (x) =2𝑥𝑥−1−(𝑥2+8)𝑥−12 =𝑥2−2𝑥−8𝑥−12;𝑥2−2𝑥−8𝑥−12=0 ⟹𝑥2−2𝑥−8=0,𝑥−12≠0, ⟹𝑥=−2,𝑥=4;𝑥≠1,f(-2) =(−2)2 +8−2−1 = -4;f(-3) =(−3)2 +8−3−1 = - 174=− 4,25;f(0) =02 +80−1= -8;max f(x)= f(-2) = -4; [-3; 0]min f(x)= f(0) = - 8.[-3; 0] 

№ 41.3. 1) f(x) =100−𝑥2, [-6; 8];f’ (x) =12100−𝑥2 ∙ (100 – x2)’ = −2𝑥2100−𝑥2 = -𝑥100−𝑥2;-𝑥100−𝑥2=0; ⟹ 𝑥=0;𝑥≠ ±10,f(0) =100−0=10;f(-6) =100−36=8;f(8) = 100−64=6;max f(x)= f(0) =10; [-6; 8]min f(x)= f(8) = 6.[-6; 8] 

№ 41.5. 1) f(x) =sin x – cos x, [0; π];f’ (x) = cos x + sin x ;cos x + sin x =0/ cos x ≠0,tg x = - 1, x =-𝜋4 +πn, n ∈ Z,x= 3𝜋4f(3𝜋4) = sin 3𝜋4 – cos3𝜋4 = 22+22 =2;f(0) =sin 0 – cos 0= -1;f(π) =sin π – cos π= 1;max f(x)= f(3𝜋4) =2; [0; π]min f(x)= f(0) = -1. [0; π] 

№41.7. Подайте число 8 у вигляді суми двох таких невід’ємних чисел, щоб добуток одного із цих чисел і куба другого числа був найбільшим. Розв'язання. Нехай x (x≥ 0) – одне з таких чисел, тоді (8 – х) – інше число (x≤ 8) .f(x) = (8 – x) x3 ,f’(x) = (8x3 – x4)’ = 24x2 – 4x3,24x2 – 4x3 = 0,4x2(6 – x) = 0,x1 = 0 або x2 = 6,f(0) =8 ∙ 0= 0, f(8) =0, f(6) =2 ∙ 216= 532 ⇒ max f(x)= f(6) =532, [0; 8]Одне число – 6, тоді інше – 2. В.: 8 = 6 + 2  

№41.11. Розбийте число 180 на три таких невід’ємних доданки, щоб два з них відносились як 1 : 2, а добуток усіх трьох доданків був найбільшим. Розв'язання. Нехай x (x≥ 0) – одне з таких чисел, тоді 2x – друге число, третє число – (180 – 3x) (x≤ 60) . Тобто, x ∈ [0; 60].f(x) = x ∙ 2x (180– 3x) = 360x2 – 6x3 ,f’(x) = (360x2 – 6x3)’ = 720x – 18x2,720x – 18x2 = 0,18x(40 – x) = 0,x1 = 0 або x2 = 40, f(0) =0, f(40) =192000,f(60) =0 ⇒ max f(x)= f(40) = 192000, [0; 60]Одне число – 40, друге – 80, третє - 60. В.: 180 = 40 + 80 + 60.

№41.13.•• У трикутник ABC вписано прямокутник так, що дві його вершини лежать на стороні AC, а дві інші — на сторонах AB і BC. Знайдіть найбільше значення площі такого прямокутника,якщо AC = 12 см, BD = 10 см, де BD — висота трикутника ABC. Розв'язання. S пр= ab, ⊿ FBG ~ ⊿ ABC⇒ 10−𝑎10=𝑏12 ⇒b=1,2(10-a) =12 -1,2a,S пр= 12a -1,2a2,S ‘пр= 12 – 2,4a,12 – 2,4a =0,a = 5, ⇒ b =6, S пр = 30 В.: 30 см2 

Самостійно опрацюйте, будь ласка, № 41.2(1,2), 41.6(1), 41.8, 41.14 ДЯКУЮ ЗА УВАГУ!ДО ПОБАЧЕННЯ!