Найкрасивіші теореми в математиці

Найкрасивіші теореми в математиці: рівняння Ейлера

Що може бути більш містичним, ніж уявне число, що взаємодіє з реальними числами, щоб нічого не створити? Читач журналу «PhysicsWorld» у 2004 році задав запитання, щоб підкреслити красу рівняння Ейлера: «e в степені i помноженого на пі дорівнює мінус одиниці».

​

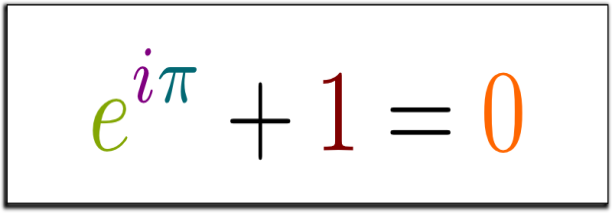
Ще раніше, в 1988 році, математик Девід Уеллс, писав статті для американського математичного журналу TheMathematicalIntelligencer, склав список з 24 теорем математики і провів опитування, попросивши читачів своєї статті вибрати найкрасивішу теорему. І після того, як з великим відривом в ньому виграло рівняння Ейлера, воно отримало звання «найкрасивішого рівняння в математиці».

​

Леонарда Ейлера називають найпродуктивнішим математиком за всю історію. Інших видатних математиків надихали його роботи. Один з кращих фізиків у світі, Річард Фейнман, в своїх знаменитих лекціях з фізики назвав рівняння Ейлера «найвизначнішою формулою в математиці». Ще один приголомшливий математик, Майкл Атья, назвав цю формулу "... математичним аналогом фрази Гамлета -« бути чи не бути »- дуже короткою, дуже стислою, і в той же час дуже глибокою".

Існує безліч цікавих фактів про зрівняння Ейлера. Наприклад, воно зустрічалося в деяких епізодах «Сімпсонів».

​

​

Також рівняння Ейлера стало ключовим пунктом в кримінальній справі. У 2003 році аспірант Каліфорнійського технологічного інституту Біллі Коттрелл писав фарбою на чужих спортивних автомобілях рівняння Ейлера. На суді він сказав: "Я знав теорему Ейлера з п'яти років, і її зобов'язані знати всі".

​

Марка, випущена в 1983 році в Німеччині в пам'ять про двохсотріччя від смерті Ейлера.

​

Марка, випущена Швейцарією в 1957 році на честь 250-ї річниці Ейлера.

Чому рівняння Ейлера так важливо?

Ви маєте повне право запитати: чому Біллі Коттрелл вважав, що про рівняння Ейлера зобов'язані знати всі? І був настільки в цьому впевнений, що почав писати його на чужих машинах? Відповідь проста: Ейлер скористався трьома фундаментальними константами математики і застосував математичні операції множення і піднесення до степеня, щоб записати красиву формулу, що дає в результаті нуль або мінус один.

• Константа e пов'язана зі степеневими функціями
• Константа i є не дійсним, а уявним числом, рівним квадратному кореню з мінус одиниці.
• Знаменита константа π (пі) пов'язана з кругами.

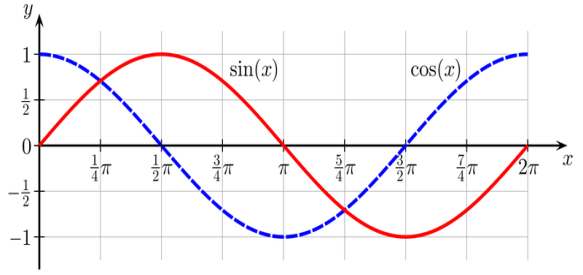
Вперше тотожність Ейлера з'явилася в 1748 році в його книзі Introductioinanalysininfinitorum. Пізніше інші люди побачили, що ця формула пов'язана з тригонометричними функціями синуса і косинуса, і цей зв'язок є дивним, адже степенева функція прямує до нескінченності, а тригонометричні функції коливаються в інтервалі від 1 до -1.

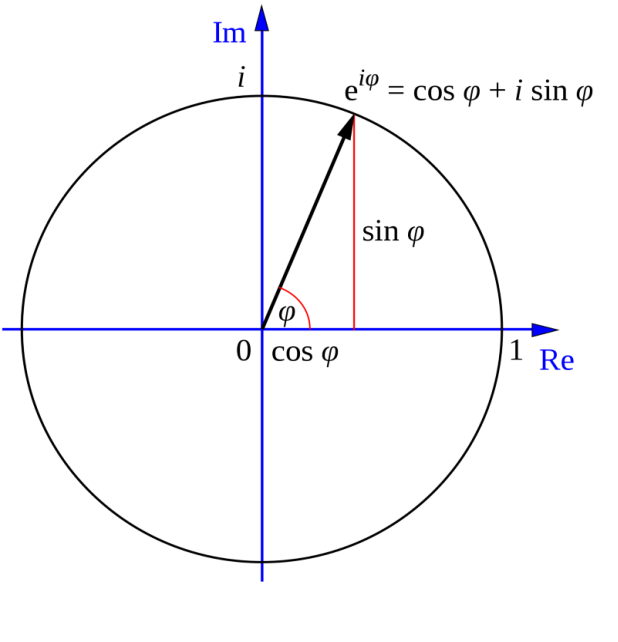
e в степені i, помноженому на φ (фі) = cos φ + i *sin φ

​

​

*графік тотожності Ейлера.

​

Показані вище рівняння і графи можуть здатися абстрактними, але вони важливі для квантової фізики і обчислень обробки зображень, і при цьому залежать від тотожності Ейлера.

1: число для рахунку

Число 1 (одиниця) є основою нашої системи числення. З неї ми починаємо рахунок. Але як ми рахуємо? Щоб рахувати, ми використовуємо цифри 0-9 і систему розрядів, визначальну значення цифри. Наприклад, число 323 означає 3 сотні, 2 десятка і 3 одиниці. Тут число 3 виконує дві різні ролі, які залежать від його розташування. 323 = (3 * 100) + (2 * 10) + (3 * 1)

0: число для позначення нічого

Деякі цивілізації використовували прогалини, щоб, наприклад, відрізняти число 101 від 11. Через якийсь час почало з'являтися особливе число - нуль. Наприклад, в печері в індійському місті Гваліор археологи виявили на стіні число 270, в якому був нуль. Найперше зафіксоване використання нуля можна побачити в Бодліанскій бібліотеці.

​

Приблизно 1400 років тому були записані правила обчислень з нулем. Наприклад, при додаванні від'ємного  числа і нуля виходить те саме від'ємне число. Ділення  на нуль не допускається.

Пі (π): найвідоміше ірраціональне число

Пі - найпопулярніше з відомих нам ірраціональних чисел. Пі можна знайти двома способами: обчисливши співвідношення довжини кола до  діаметра, або співвідношення площі кола до квадрату його радіуса. Евклід довів, що ці співвідношення постійні для всіх кіл, навіть для місяця, шини і т.д.

На даний момент комп'ютери змогли обчислити всього 2,7 трильйона розрядів пі. Може здаватися, що це багато, але насправді цей шлях нескінченний.

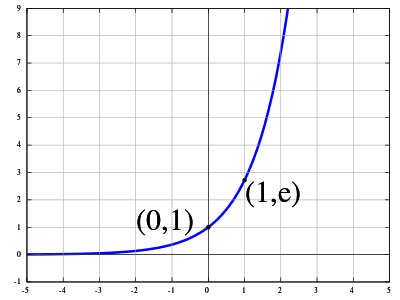
e: історія експоненціального зростання

e - це ще одне знамените ірраціональне число. Дрібна частина e теж нескінченна, як і у пі. Ми використовуємо число e для обчислення статечного (експоненціального) зростання. Іншими словами, ми використовуємо e, коли бачимо дуже швидке зростання або зменшення.

Один з найбільших, а можливо і кращий математик Леонард Ейлер відкрив число e в 1736 році і вперше згадав це особливе число в своїй книзі Mechanica.

Щоб розібратися в експоненціальному зростанні, ми можемо використовувати історію про винахідника шахів. Коли він придумав цю гру, то показав її володарю Півночі. Царю сподобалася гра і він пообіцяв, що віддасть автору будь-яку нагороду. Тоді винахідник попросив щось дуже просте: 20 зерен на першу клітку шахівниці, 21 зерно на другу клітку дошки, 22 зерна - на третю, і так далі. Щоразу кількість зерен подвоювалася. Цар Півночі подумав, що прохання буде виконати легко, але він помилявся, бо на останню клітку потрібно було б покласти 263 зерен, що дорівнює 9 223 372 036 854 775 808. Це і є експоненціальне зростання. Воно почалося з 1, постійно подвоювалося, і через 64 ​​кроки виросло у величезне число!

Число e відкрив Ейлер. Однак Якоб Бернуллі теж працював з числом e, коли обчислював складний відсоток, щоб заробити більше грошей. Якщо вкласти 100 доларів під 10% доходу, то як буде рости ця сума? По-перше, це залежить від того, як часто банк розраховує відсотки. Наприклад, якщо він розраховує один раз, то ми отримаємо в кінці року 110 доларів. Якщо ми передумали і будемо брати відсотки кожні 6 місяців, то в цьому випадку ми отримаємо більше 110 доларів. Справа в тому, що відсоток, отриманий за перші 6 місяців, теж отримає свій відсоток. Загальна сума буде дорівнює 110,25 доларів. Можна здогадатися, що ми можемо отримати більше грошей, якщо будемо забирати гроші кожен квартал року. А якщо ми будемо робити часовий інтервал все коротше, то остаточні суми будуть продовжувати рости. Такий нескінченний складний відсоток зробить нас багатими! Однак наш загальний дохід прагне до обмеженого значення, пов'язаному з e.

Бернуллі не називав число 2,71828 ім'ям e. Коли Ейлер працював з 2,71828, він звів експонентну функцію e в степінь x. Свої відкриття він виклав в книзі TheAnalysisofInfinite.

У 1798 році Томас Мальтус використовував експонентну функцію в своєму есе, присвяченому харчовому дефіциту майбутнього. Він створив лінійний графік, що показує виробництво їжі і експонентний графік, що показує населення світу. Мальтус зробив висновок, що в далекій перспективі експоненціальне зростання переможе, і світ чекає серйозний дефіцит їжі. Це явище назвали «мальтузіанською катастрофою». Ньютон теж використовував цю модель, щоб показати, як охолоджується чашка чаю.

Уявність числа: i, квадратний корінь -1

Довгий час для вирішення своїх завдань математикам було досить звичайних чисел. Однак в якийсь момент для подальшого розвитку їм потрібно відкрити щось нове і загадкове. Наприклад, італійський математик Кардано намагався розділити число 10 на 2 частини, добуток яких дорівнював би 40. Щоб вирішити цю задачу, він записав рівняння: x (10-x) = 40. Коли він вирішив це квадратне рівняння, то отримав два рішення: 5 плюс √-15 і 5 мінус √-15, що в той час не мало ніякого сенсу. Цей результат був безглуздим, тому що за визначенням квадратного кореня йому потрібно було знайти число, квадрат якого був би від'ємним. Однак і додатні, і відємні  числа в квадраті мають додатне  значення. Як би там не було, він знайшов своє унікальне число. Однак першим математиком, який назвав √-1 (квадратний корінь з мінус одиниці) уявним числом i, був Ейлер.

Найкрасивіше рівняння: тотожність Ейлера

Тотожність Ейлера пов'язує експонентну функцію з функціями синуса і косинуса, значення яких коливаються від мінус одиниці до одиниці. Щоб знайти зв'язок з тригонометричними функціями, ми можемо представити їх у вигляді нескінченного ряду, істинного для всіх значень​

Ейлер ніколи не записував цю тотожність в явному вигляді, і ми не знаємо, хто вперше записав її. Проте, ми пов'язуємо її з ім'ям Ейлера в знак поваги перед цим великим першопрохідцем математики.