ПЛАН-КОНСПЕКТ ЗАЛІКОВОГО(ВІДКРИТОГО) УРОКУ

Дата проведення уроку: «____»   листопада   2020р Тема  уроку: «Найпростіші перетворення графіків функції».

Мета уроку: 

v навчальна: удосконалити вміння учнів будувати графіки функцій, застосовуючи геометричні перетворення; за поданим графіком записувати формулу, що задає функцію; розв’язувати рівняння графічним способом;

v розвивальна: розвивати логічне та творче мислення, увагу, уяву, кмітливість; формувати навички роботи з графічною інформацією, комунікативні компетенції учнів;

v виховна: виховувати графічну культуру, вміння самоорганізовуватися, активізувати інтерес до пізнання нового. 

Тип уроку: застосування знань, умінь та навичок;

Обладнання: підручник алгебра 9 клас, план-конспект уроку, дошка, крейда, указка, ППЗ, проектор, ноутбук,навчальна презентація,  роздатковий матеріал.

Компетенції учнів на уроці:

План уроку  та дозування часу:

Методика та прийоми проведеного заняття: 

vметоди:репродуктивний,        частково     пошуковий,          спонукальний, розповідь, бесіда;

vприйоми: спонукання, взаємоконтролю, самоконтролю, активізація уваги та мислення, ілюстрації.

Використана методична  література:

1. Алгебра: підруч. для 9 кл. загальноосвіт. навч. закл. / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – Х.: Гімназія, 2017. –272 с.

Хід уроку:

Етап 1. Організація класу.

Заходжу в клас, вітаюся з учнями.

Пропоную учням  сісти і підготувати все необхідне для уроку. Відмічаю відсутніх. 

Сьогодні у нас не зовсім звичайний урок. До нас завітали гості. Давайте пригадаємо, яку тему ми зараз вивчаємо? («Функції») Спробуйте розшифрувати слово «функція»:

Ф – фантазія                                               Ц – цілеспрямованість

У – уміння                                                   І – ініціативність

Н - наполегливість                                 Я – знаю, вмію, можу К – кмітливість                                                

Епіграф уроку: 

                                   Немає жодної галузі людських знань, куди б не                                       входило поняття функції та її графічного зображення.

                                                                                                        К.Ф.Лебединцев

Перевірка виконання  д/з(взаємоперевірка за готовими розв’язками).

Роздаю кожному учню картку само оцінювання.

Форми навчання на даному етапі: колективна

Методи навчання на даному етапі: розповідь, бесіда

Засоби  навчання на даному етапі: ручка, журнал, записник, мультимедійний комплекс.

Етап 2. Мотивація навчальної діяльності

Зробіть висновок, чи варто вивчати цю тему? Чи так уже необхідні нам знання про функцію?  Так, необхідні! Адже функція – це одне з основних математичних понять, що виражає залежність між змінними величинами, які існують не лише в природі, а й спостерігаються в соціальних явищах, і тому присутні в кожній області знань. Це підтверджує і зміст епіграфа уроку: «Немає жодної галузі людських знань, куди б не входило поняття функції та її графічного зображення».

Пропоную переглянути презентацію про практичне застосування графіків функцій в житті людини.

Сьогодні ми узагальнимо знання про геометричні перетворення графіків функцій та вдосконалимо вміння їх застосовувати для побудови графіків. Отже, запишіть тему уроку: «Перетворення графіків функцій».

Форми навчання на даному етапі: колективна;

Методи навчання на даному етапі: розповідь, бесіда

Засоби  навчання на даному етапі: дошка, крейда, мультимедійний комплекс

Етап 3. Актуалізація опорних знань учнів. 

Бліц-опитування:

1.     Користуючись слайдами, назвіть основні види функцій (лінійна, обернена пропорційність, у=│x│, у=х

2.     Які перетворення можна робити з графіками функцій?  

3.     Запишіть рівняння функцій, що відповідають  поданим графікам.

Форми навчання на даному етапі: індивідуальна

Методи навчання на даному етапі: репродуктивні Засоби  навчання на даному етапі: дошка, крейда, мультимедійний комплекс.

Етап 4. Удосконалення знань і умінь

Розв’язування вправ з підручника: № 9.13, 10.15 с. 83, 93 Розв’язки:

9.13. Запишемо такі перетворення щоб отримати графік заданої функції: . Згідно даних перетворень побудуємо графіки:

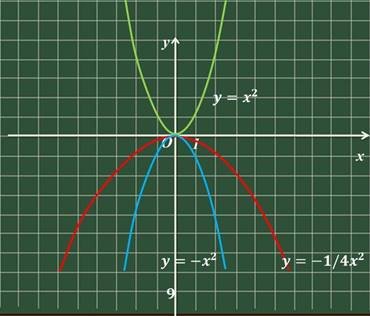
10.15. Запишемо такі перетворення щоб отримати графік заданої функції:

𝑥² → (𝑥 + 5)² → (𝑥 + 5)² − 9. Згідно даних перетворень побудуємо графіки:

1) 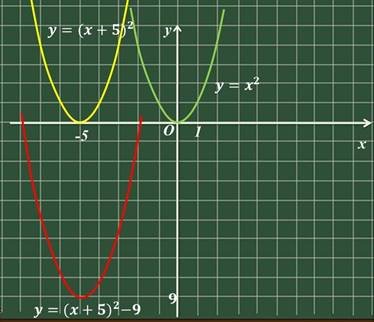 у = 0, х = - 2; - 8;

2)  𝑦 > 0, 𝑥 ∈ (−∞; −8) ∪

(−2; +∞)  

3)  𝑦 ↑ : 𝑥 ∈ (−5; +∞)

𝑦 ↓ : 𝑥 ∈ (−∞; −5)

4)𝑦 ∈ (−9; +∞)

Графічний диктант:

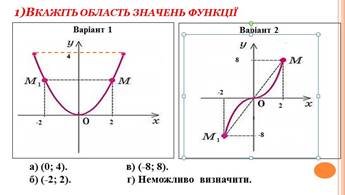
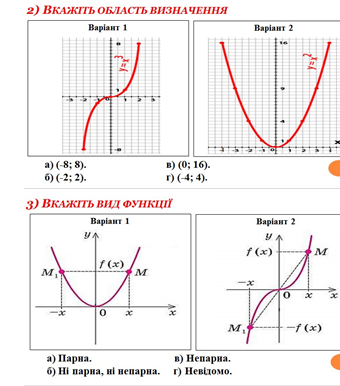
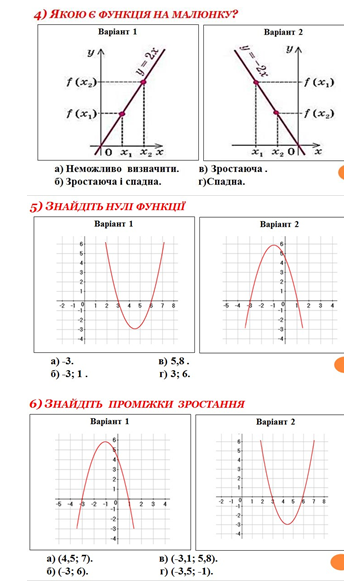
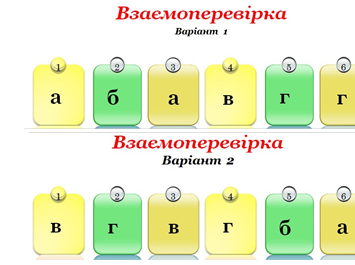
Форми навчання на даному етапі: індивідуально - групова

Методи навчання на даному етапі: розповідь, бесіда, приклад

Засоби  навчання на даному етапі: підручник, план –конспект, крейда, дошка, указка, мультимедійний комплекс.

Етап 5. Підведення підсумків уроку

Рефлексія:

vЧи задоволені ви своєю роботою?

vЗ яким настроєм ви працювали на уроці? 

vЩо вам запам’яталось на уроці? 

vЧи було вам комфортно на уроці?

vДе вам стануть в пригоді здобуті знання?

В кінці уроку  перевіряю точність і якість виконання роботи. 

Відмічаю учнів, які успішно виконали завдання, вказую на помилки, які допущені учнями.  Учні виставляють бали за роботу на уроці «Картки оцінювання», виводять середній бал.

Форми навчання на даному етапі: колективна

Методи навчання на даному етапі: розповідь, бесіда

Засоби  навчання на даному етапі: журнал, ручка, щоденник

Етап 6. Постановка домашнього завдання 

А тепер запишіть будь-ласка в щоденники домашнє завдання. З підручника 

§ 9-10 с .77-90  № 9.14, 10.16 с. 83, 93

Форми навчання на даному етапі: колективна.

Методи навчання на даному етапі: розповідь, бесіда.

Засоби  навчання на даному етапі: крейда, дошка , мультимедійний комплекс.