Нескінченна спадна геометрична прогресія зі знаменником |q| < 1 там сума.

Тема. Нескінченна спадна геометрична прогресія зі знаменником |q| < 1 там сума.

Мета. Познайомити учнів з нескінченними спадними геометричними прогресіями зі знаменником |q| < 1. Ввести поняття суми не­скінченної спадної геометричної прогресії, вивести формулу для знаходження суми. Формування в учнів уміння застосовувати ви­ведену формулу до розв'язування вправ.

I. Перевірка домашнього завдання

1. Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при їх виконанні. Уч­ні перевіряють свої розв'язання за записами, зробленими на дошці до початку уроку.

Вправа № 264 (а)

.

Відповідь. .

Вправа № 265 (а)

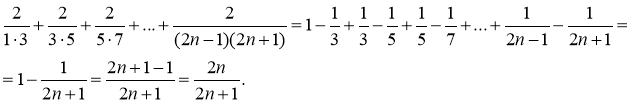
Відповідь. .

Вправа № 265 (г)

Чисельник дробу одиницю можна подати  у вигляді добутку суми і різниці коренів, що стоять у знаменнику:

Тоді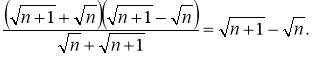

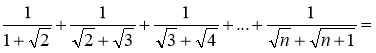
Відповідь. .

2. Виконання вправи № 265 (є).

II. Формування поняття нескінченної спадної геометричної прогресії та її суми

Розглянемо квадрат зі стороною 1. Візьмемо його половину, потім половину частини, що залишилася, і т. д. (рис. 151). Площі заштрихованих прямокутників утворюють геометричну прогре­сію , , , , , , …, зна­менник якої дорівнює q = .

Із рис. 151 видно, що заштрихо­вані прямокутники заповнюють увесь квадрат. Доречно вважати, що сума площ всіх заштрихованих прямокут­ників дорівнює 1, тобто + + + + + + … + = 1.

У лівій частині цієї рівності за­писано суму нескінченного числа до­данків.

До сьогоднішнього уроку ми розглядали суми тільки зі скінчен­ним числом доданків. Для надання змісту виразу в лівій частині останньої рівності розглянемо суму п перших членів:

S_n = + + + … + .

За формулою суми п перших членів геометричної прогресії маємо:

.

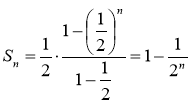Якщо п необмежено збільшується (пишуть n → ∞), то вираз наближається до нуля (пишуть → 0), а вираз 1 – наближається до 1.

Отже, , якщо n → ∞.

Таким чином, сумою нескінченної спадної геометричної про­гресії називається число, до якого наближається сума п перших членів цієї прогресії, якщо п нескінченно збільшується.

Виведемо формулу суми нескінченної спадної геометричної прогресії

b₁ + b₁q + b₁q² + b₁q³ + …, знаменник якої |q| < 1.

За формулою суми п перших членів геометричної прогресії маємо:

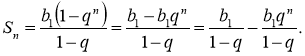
Якщо |q| < 1, то при необмеженому збільшенні п вираз qⁿ пря­мує до нуля, при цьому вираз теж прямує до нуля.

Отже, 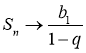  при п → ∞.

Таким чином, сума S нескінченної спадної геометричної про­гресії дорівнює:

.

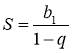Зокрема, якщо b₁ = 1, то маємо .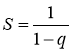

Формули 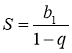, 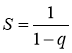справедливі тільки для |q| < 1.

Розглянемо приклади.

Задача 1. Знайдіть суму нескінченної спадної геометричної про­гресії 9; 3; 1; ... .

Розв'язання

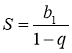Оскільки b₁ = 9, q = , то за формулою маємо

.

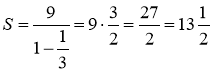Відповідь. .

Задача 2. Знайдіть суму нескінченної спадної геометричної про­гресії, якщо b₄ = , q = .

Розв'язання

Використовуючи формулу b_n = b₁q^n-1 при п = 4, знайдемо b₁:

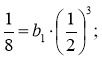b₁ = 1.  Тоді за формулою 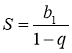маємо: .

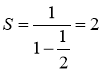Відповідь. 2.

Виконання вправ     

Вправи № 267 (б, г), 268 (б, г), 269, 270.

III. Домашнє завдання

§ 62 (від кінця приклада 2); № 267 (а, в), № 268 (а, в).

IV. Підведення підсумків уроку

Запитання до класу

1. Яка геометрична прогресія називається нескінченною спадною?
2. Що розуміють під сумою нескінченної спадної геометричної прогресії?
3. За якою формулою можна обчислити суму нескінченної спад­ної геометричної прогресії?
4. Знайдіть суму нескінченної спадної геометричної прогресії:

а) 1 + + + + … ;   б) 1 + + + + … ;  в) 1 + + + + … .