Використання графіків у задачах різного типу. Розв'язування задач з параметрими за допомогою графіків
1
Департамент освіти Харківської міської ради
Комунальний заклад «Харківський фізико-математичний ліцей № 27
Харківської міської ради Харківської області»
«Використання графіків у задачах різного типу.
Розв’язування задач з параметрами за допомогою графіків»
Харік Олена Юхимівна,
вчитель математики,
вищої кваліфікаційної категорії,
вчитель-методист
комунального закладу «Харківський
фізико-математичний ліцей № 27
Харківської міської ради
Харківської області»
Зміст
Вступ.........................................................................
Актуальність
Мета роботи
Завдання роботи
Історіографічний аспект
Методична новизна
Практичне значення
Особистий внесок
Апробація
1. Використання властивостей функцій при розв’язуванні ірраціональних і трансцендент- них рівнянь......
1.1. Методи побудови графіків функцій
1.2. Область визначення функції
1.3. Множина значень функції
1.4. Монотонність функції.
1.5. Екстремуми функції («мінімакс»)
Висновок до першого розділу
2. Розв’язування задач з параметрами за допомогою графіків
2.1. Рівняння, які містять суму модулів лінійних функцій
2.2. Рівняння, які містять різницю модулів лінійних функцій
2.3. Застосування властивостей квадратичної функції
2.4. Розв’язування систем з параметрами
Висновок до другого розділу
Висновки......................................................................
Список літератури та Інтернет – ресурси............................................
Анотація.......................................................................
Однією з провідних змістових ліній в шкільному курсі математики у відповідності з Державним стандартом освіти є функціональна спрямованість цього курсу.
Актуальність
Дослідження властивостей функцій у тій чи іншій формі має супроводжувати вивчення математики протягом усього навчання. Первинне ознайомлення з поняттям функції починається у 6 класі, поглиблюється протягом наступних років: у 7 класі - вивчається лінійна функція, у 8-9 – дробово-лінійна та квадратична.
Доцільно вже в цих класах ознайомлювати учнів з методами перетворення графіків функцій: паралельним перенесенням, осьовою симетрією, додаванням графіків. При цьому слід постійно звертати увагу учнів на зв’язок таких понять, як функція, рівняння, нерівність. Зокрема, необхідно домагатись від учнів розуміння того, що розв’язування рівняння f(x) = 0 та нерівності f(x) > 0 є окремими складовими задачі дослідження функції y = f(x) (знаходження нулів функції та проміжків її знакосталості).
У старших класах вивчаються тригонометричні функції, степенева, показникова, логарифмічна функції, вводиться поняття оберненої функції. Під час вивчення функцій слід зробити наголос на моделюванні реальних процесів. Учні мають асоціювати характер реального процесу з відповідною функцією, її графіком, властивостями. Важливо, щоби притаманні явищу властивості пов’язувались із властивостями функцій (спадання, зростання, прямування до певної границі). Зазначимо, що використання властивостей функцій для розв’язування практичних задач підсилює прикладну спрямованість шкільного курсу математики.
Мета роботи
Основною метою даної роботи є демонстрація наочного уявлення про використання властивостей функцій для розв’язування рівнянь; а також графіків функцій та графіків рівнянь для розв’язування систем рівнянь.
Завдання роботи
Однією з проблем, яка вирішується в даній роботі, є залучення всіх зацікавлених осіб до розвитку креативних здібностей учнів, формування нестандартного мислення, вміння розв’язувати задачі підвищеної складності, які потребують нових підходів.
Окрема роль у розвитку математичних здібностей учнів належить системі вправ, що містять модулі та параметри. Найефективніші методи розв’язування цих вправ – графічні.
Історіографічний аспект
Питання методики використання графіків у задачах різного типу розкрито в роботах провідних вчителів-методистів України, зокрема, М.С.Якіра, В.Б. Полон-
ського [4], Г.В. Апостолової [2]; цікаві вправи наведено в роботах [1]; [3]; [5]; [6].
Багато уваги питанням використання графіків функцій для розв’язання рівнянь з модулями учнями 6-7 класів приділяє автор даної роботи в посібнику [7].
Методична новизна
Побудова графіків функцій з використанням геометричних перетворень та методу додавання графіків за допомогою дослідження швидкостей спадання та зростання функцій; використання властивостей функцій для розв’язання задач підвищеної складності на прикладах авторських задач.
Практичне значення
Робота має практичне значення для вчителів та учнів при підготовці до змагань різного рівня (олімпіад, турнірів тощо) та ДПА, ЗНО. Може бути використана для проведення факультативних занять та курсів підвищення кваліфікації вчителів математики.
Особистий внесок
Особистий внесок автора полягає в складанні авторських задач спеціального типу, що демонструють ефективність методів застосування властивостей функцій і графіків для розв’язування нестандартних завдань та задач з параметрами.
Апробація
Матеріал даної роботи проходив апробацію протягом трьох років у комунальному закладі «ХФМЛ №27» та під час проведення літньої школи для учнів 7-10 класів міста Харкова
1. Використання властивостей функцій при розв’язуванні ірраціональних і трансцендентних рівнянь
Зазвичай в шкільному курсі математики учнів навчають стандартним методам розв’язування рівнянь. Але все частіше, особливо на конкурсних випробовуваннях і олімпіадах різного рівня, трапляються рівняння, розв’язування яких стандартними методами є громіздким або майже неможливим. І саме застосування властивостей функцій дає можливість вирішення проблеми.
1.1. Методи побудови графіків функцій
Продемонструємо основні методи побудови графіків функцій та дослідження їх властивостей, розглянувши приклади побудови графіків функцій.
Приклад 1.1.1. Побудувати графік функції ![]() .
.
На цьому прикладі нагадаємо загальну схему дослідження функції, що передує побудові графіка.
1) Область визначення ![]() , або
, або![]() R\
R\![]() ,
,
2) асимптоти: вертикальна ![]() і похила
і похила ![]() ,
,
3) проміжки знакосталості: при ![]()
![]() ; при
; при ![]()
![]() ,
,
![]() 4) дослідження на монотонність та екстремуми зазвичай в старших класах виконують за допомогою першої похідної: та метода інтервалів:
4) дослідження на монотонність та екстремуми зазвичай в старших класах виконують за допомогою першої похідної: та метода інтервалів:
![]()
 Рис.1.1
Рис.1.1
Отже, функція монотонно зростає при ![]() та при
та при ![]() ; монотонно спадає при
; монотонно спадає при ![]() та при
та при ![]() ; при
; при ![]() має локальний максимум:
має локальний максимум: ![]() , при
, при ![]() має локальний мінімум:
має локальний мінімум:![]() ,
,
5) множина значень ![]() ,
,
6) графік
![]()
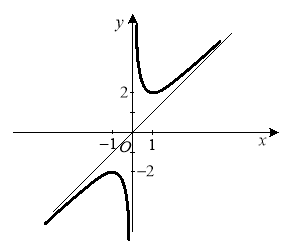 Рис.1.2
Рис.1.2
Зауважимо, по-перше, що для запису проміжків монотонності функції не можна використовувати знак об’єднання множин, тобто запис: функція монотонно спадає при ![]() є помилковим. Побудуємо контрприклад: нехай
є помилковим. Побудуємо контрприклад: нехай ![]() , тоді з нерівності
, тоді з нерівності ![]() випливає
випливає ![]() , отже, функція зростає!
, отже, функція зростає!
По-друге, у 8 – 9 класах дослідити дану функцію на екстремуми можна за допомогою нерівності Коші про середнє арифметичне та середнє геометричне двох чисел: 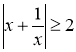 ; нерівність перетворюється на рівність при
; нерівність перетворюється на рівність при ![]() ;
; ![]() .
.
Приклад 1.1.2. Побудувати графік функції ![]() .
.
Для побудови графіка цієї функції застосуємо метод геометричних перетворень.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
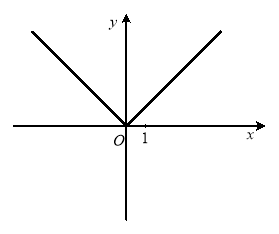
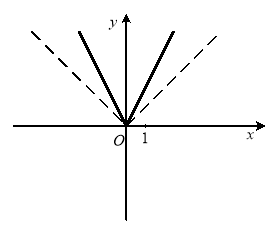
Рис. 1.3 Рис. 1.4
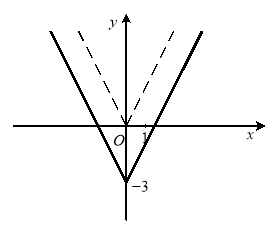
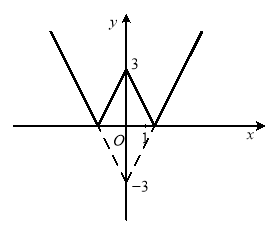
Рис. 1.5 Рис. 1.6
Приклад 1.1.3. Побудувати графік функції ![]() .
.
Для побудови графіка даної функції розглянемо окремо графіки функцій ![]() та
та ![]() , які отримаємо за допомогою паралельного перенесення графіка функції
, які отримаємо за допомогою паралельного перенесення графіка функції ![]() та виконаємо додавання з урахуванням зміни швидкості зростання та спадання кожного з доданків.
та виконаємо додавання з урахуванням зміни швидкості зростання та спадання кожного з доданків.
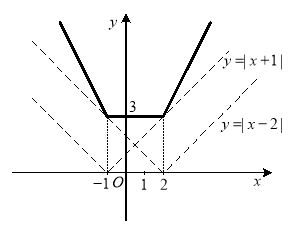 Рис. 1.8
Рис. 1.8
Приклад 1.1.4. Побудувати графік функції ![]() .
.
Для побудови графіка даної функції скористуємося окремими кроками попереднього приклада - побудуємо графіки функцій ![]() та
та ![]() та виконаємо додавання з урахуванням зміни швидкості зростання та спадання кожного з доданків.
та виконаємо додавання з урахуванням зміни швидкості зростання та спадання кожного з доданків.
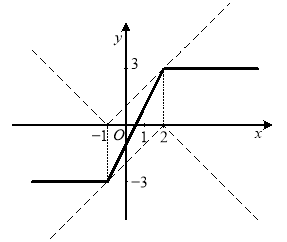
Рис. 1.9
Розглянемо декілька груп рівнянь, при розв’язуванні яких використовують певні властивості функцій.
1.2. Область визначення функції
Приклад 1.2.1. Розв’язати рівняння:
![]()
Приклад 1.2.2. Розв’язати рівняння:
![]()
Для знаходження розв’язків кожного з цих рівнянь достатньо знайти область визначення.
Область визначення першого з них - пуста множина, бо система:
![]()
![]()
- несумісна, отже, перше рівняння коренів не має.
Відповідь: коренів немає.
Область визначення другого рівняння містить єдине число 0: 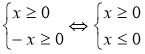
Згідно перевірки - це число є його коренем.
Відповідь: 0.
Для знаходження розв’язків кожного з наступних рівнянь достатньо знайти множини значень функцій лівої та правої частин рівнянь.
Приклад 1.3.1. Розв’язати рівняння:
![]()
Перше рівняння не має коренів, бо множина значень функції у лівій частині рівняння – множина невід’ємних чисел, але права частина рівності - від’ємне число.
Відповідь: коренів немає.
Приклад 1.3.2. Розв’язати рівняння:
![]()
Множина значень функції лівої частини рівняння - це множина невід’ємних чисел, але множина значень функції правої частини – це множина недодатніх чисел (![]() ). Рівність (1.3.2) може виконуватися, якщо множина значень кожної з функцій містить єдине число: 0. Це значення функції набувають при
). Рівність (1.3.2) може виконуватися, якщо множина значень кожної з функцій містить єдине число: 0. Це значення функції набувають при ![]() , отже, маємо єдиний корінь рівняння: число 1.
, отже, маємо єдиний корінь рівняння: число 1.
Відповідь: 1.
Використаємо відомі теореми математичного аналізу та надамо їх геометричну інтерпретацію.
Теорема 1 (існування та єдиності). Якщо функція ![]() неперервна та монотонна на деякій множині D, то для будь-якого числа М, що належить множині значень цієї функції, існує єдине число , для якого виконується рівність
неперервна та монотонна на деякій множині D, то для будь-якого числа М, що належить множині значень цієї функції, існує єдине число , для якого виконується рівність ![]()
Графічна ілюстрація до теореми 1 ( рис.1.10):
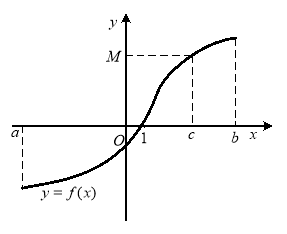
Рис.1.10
Теорема 2. Якщо рівняння має вигляд![]() , де функція
, де функція ![]() - зростає, функція
- зростає, функція ![]() - спадає, то воно має не більше одного кореня.
- спадає, то воно має не більше одного кореня.
Графічна ілюстрація до теореми 2 ( рис.1.11 та рис 1.12):
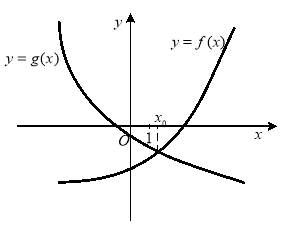
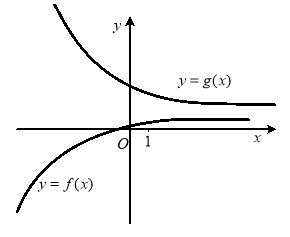
Рис.1.11 Рис.1.12
Розглянемо приклади.
Приклад 1.4.1. Розв’язати рівняння:
![]()
Приклад 1.4.2. Розв’язати рівняння:
![]()
Приклад 1.4.3. Розв’язати рівняння:
![]()
Розв’язування рівнянь цієї групи ґрунтується на використанні важливої властивості функцій - монотонність.
Для рівняння (1.4.1) множина ![]() =
= ![]() і функція
і функція
![]()
![]() монотонно зростає на цій множині, бо є сумою
монотонно зростає на цій множині, бо є сумою
монотонно зростаючих функцій. Тому, якщо корінь існує, то він - єдиний. Згідно перевірки ![]() задовольняє дану рівність:
задовольняє дану рівність: ![]() . Отже, число 2 – єдиний корінь рівняння (1.4.1).
. Отже, число 2 – єдиний корінь рівняння (1.4.1).
Відповідь: 2.
Корінь рівняння (1.4.2) - це число 1, але те, що він єдиний, стверджувати не можна, бо обидві функції ![]() і
і ![]() монотонно зростають.
монотонно зростають.
Поділимо обидві частини рівняння (1.4.2) на ![]() (
(![]() ), отримаємо
), отримаємо
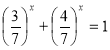
Нова функція 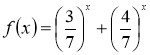 - монотонно спадає,
- монотонно спадає, ![]() , тому за теоремою 1 отримаємо: корінь 1 - єдиний.
, тому за теоремою 1 отримаємо: корінь 1 - єдиний.
Відповідь: 1.
В процесі знайомства учнів зі стандартними методами розв’язування показникових рівнянь ми пропонуємо учням рівняння
![]()
дуже схоже на рівняння (1.4.3). Стандартний метод розв’язування - заміна: нехай ![]() , (у > 0), тоді
, (у > 0), тоді 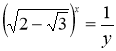 , бо
, бо ![]() .
.
Рівняння 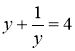 має корені
має корені ![]() і
і ![]() , які задовільняють умову у > 0. Розв’язуємо найпростіші рівняння
, які задовільняють умову у > 0. Розв’язуємо найпростіші рівняння ![]() і
і
![]() , маємо корені
, маємо корені ![]() і
і ![]() .
.
Повернемося до рівняння (1.4.3). Один корінь стає прозорим: це число 2. Його єдиність доведемо аналогічно, як і при розв’язуванні рівняння (1.4.2). Ділимо обидві частини рівняння на ![]() (
(![]() ), отримуємо:
), отримуємо: 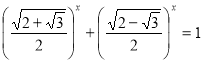
Функція 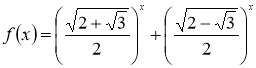 монотонно спадає, бо
монотонно спадає, бо 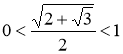
і 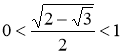 , тому з прямою у = 1 графік цієї функції перетинається не більше одного раза. Отже, рівняння (1.4.3) має єдиний корінь: число 2.
, тому з прямою у = 1 графік цієї функції перетинається не більше одного раза. Отже, рівняння (1.4.3) має єдиний корінь: число 2.
Відповідь: 2.
1.5. Екстремуми функції («мінімакс»)
Наступний метод розв’язування застосовується до рівнянь, що мають вигляд ![]() . Він ґрунтується на відомій властивості функцій, неперервних на деякому відрізку: набувати найменшого та найбільшого значення. Серед користувачів він отримав вдалу назву «мінімакс».
. Він ґрунтується на відомій властивості функцій, неперервних на деякому відрізку: набувати найменшого та найбільшого значення. Серед користувачів він отримав вдалу назву «мінімакс».
Нехай функція ![]() набуває найбільшого значення при
набуває найбільшого значення при ![]() , функція
, функція ![]() - найменшого значення при
- найменшого значення при ![]() . Тоді можна стверджувати, що
. Тоді можна стверджувати, що ![]() єдиний корінь рівняння
єдиний корінь рівняння ![]() (рис.1.13).
(рис.1.13).
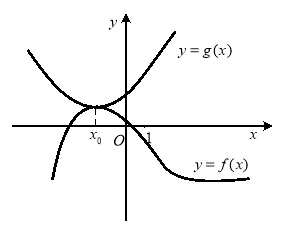
Рис. 1.13.
Примітка. Якщо найбільше та найменше значення функції ![]() і
і ![]() набувають при різних значеннях аргументу:
набувають при різних значеннях аргументу: ![]() (для
(для ![]() ) і
) і ![]() (для
(для ![]() ), тоді рівняння
), тоді рівняння ![]() не має коренів (рис. 1.14).
не має коренів (рис. 1.14).
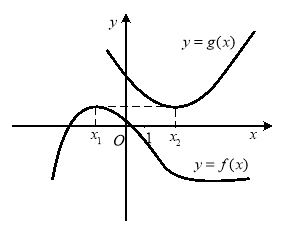
Рис. 1.14
Приклад 1.5.1. Розв’язати рівняння:
![]()
Приклад 1.5.2. Розв’язати рівняння:
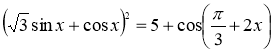
Приклад 1.5.3. Розв’язати рівняння:
![]()
Приклад 1.5.4. Розв’язати рівняння:
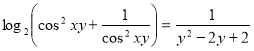
Приклад 1.5.5. Розв’язати рівняння:
![]()
![]() Розв’язування першого з рівнянь даної групи (1.5.1): найбільше значення функції
Розв’язування першого з рівнянь даної групи (1.5.1): найбільше значення функції ![]() дорівнює 2 при
дорівнює 2 при ![]() (нерівність між середнім арифметичним і середнім квадратичним двох чисел: де
(нерівність між середнім арифметичним і середнім квадратичним двох чисел: де ![]() ;
; ![]() ; рівність отримуємо тоді й тільки тоді, коли
; рівність отримуємо тоді й тільки тоді, коли ![]() ); найменше значення функції
); найменше значення функції ![]() також дорівнює 2 при
також дорівнює 2 при ![]() , бо
, бо ![]() . Отже, єдиний корінь рівняння (1.5.1) - це число 3.
. Отже, єдиний корінь рівняння (1.5.1) - це число 3.
Відповідь: 3.
Для розв’язування рівняння (1.5.2) скористаємося формулою додавання гармонічних коливань: ![]() , де кут
, де кут ![]() визначаємо зі співвідношень:
визначаємо зі співвідношень: 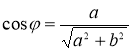 ;
; 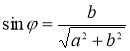 .
.
Тоді 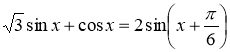 і функція
і функція ![]() набуває
набуває
найбільшого значення, яке дорівнює 4, при 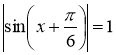 , або при
, або при ![]() (1). Найменше значення функції
(1). Найменше значення функції 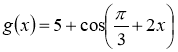 також дорівнює 4 при
також дорівнює 4 при 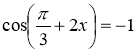 , або при
, або при ![]() (2). Серії (1) и (2) збігаються.
(2). Серії (1) и (2) збігаються.
Отже, розв’язком рівняння (1.5.2) є множина ![]() , де k - довільне ціле число.
, де k - довільне ціле число.
Відповідь: ![]() , де k - довільне ціле число.
, де k - довільне ціле число.
Перетворимо рівняння (1.5.3): ![]() . Найбільше значення функції
. Найбільше значення функції ![]() дорівнює 1 при
дорівнює 1 при ![]() , де k - довільне ціле число.
, де k - довільне ціле число.
Найменше значення функції ![]() дорівнює 1 при
дорівнює 1 при ![]() (застосували нерівність Коші між середнім арифметичним і середнім геометричним двох чисел:
(застосували нерівність Коші між середнім арифметичним і середнім геометричним двох чисел: ![]() , де
, де ![]() ,
, ![]() ; зазначимо, що нерівність перетворюється на рівність тоді й тільки тоді, коли
; зазначимо, що нерівність перетворюється на рівність тоді й тільки тоді, коли ![]() ). Але при
). Але при ![]() функція
функція ![]() набуває найбільшого значення. Отже, число 0 - єдиний корінь рівняння (1.5.3).
набуває найбільшого значення. Отже, число 0 - єдиний корінь рівняння (1.5.3).
Відповідь: 0.
Наступні рівняння відрізняються від попередніх тим, що мають дві, або навіть три змінні, але метод «мінімакс» також можна застосувати.
Розглянемо рівняння (1.5.4) і зазначимо, що 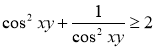 (наслідок нерівності Коші або з дослідження функції
(наслідок нерівності Коші або з дослідження функції ![]() - приклад 1.1.1).
- приклад 1.1.1).
Таким чином, 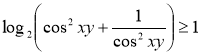 і найменше значення лівої частини рівняння дорівнює 1 при
і найменше значення лівої частини рівняння дорівнює 1 при ![]() , де
, де ![]() Z.
Z.
Розглянемо праву частину рівняння: ![]() , тоді найбільше значення правої частини дорівнює 1 при
, тоді найбільше значення правої частини дорівнює 1 при ![]() . Отже, маємо
. Отже, маємо ![]() і
і ![]() , де
, де
![]() Z.
Z.
Відповідь: (![]() ; 1), де
; 1), де ![]() Z.
Z.
Для того, щоб розв’язати рівняння (1.5.5) зазначимо:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
отже, ![]()
![]()
![]() , але за умовою
, але за умовою
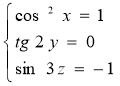
![]()
![]()
![]() , тому в кожній з нерівностей (1), (2), (3) виконується рівність. Розв’язки системи рівнянь і є розв’язками
, тому в кожній з нерівностей (1), (2), (3) виконується рівність. Розв’язки системи рівнянь і є розв’язками
даного рівняння.
Відповідь: ![]() , де k, n, m –довільні цілі числа.
, де k, n, m –довільні цілі числа.
Висновок до першого розділу
В першому розділі розглянуто основні методи побудови графіків, зокрема: за загальною схемою, за допомогою геометричних перетворень та з використанням додавання графіків на основі монотонності функцій. Надані приклади демонструють переваги використання властивостей функцій при розв’язуванні нестандартних рівнянь та рівнянь підвищеної складності.
2. Розв’язування задач з параметрами за допомогою графіків
Сучасна математична освіта має за мету виховання компетентної особистості, здатної не тільки до практичного застосування набутих знань і навичок, але й схильної до дослідницької роботи. Зважаючи на це, в шкільному курсі математики все більше уваги приділяють відповідним вправам: розв’язування рівнянь з модулями, з параметрами, які допомагають як вчителю, так і учню просуватися в напрямку реалізації цієї мети. Звичайно, велика кількість таких рівнянь може бути розв’язана аналітично, але за допомогою графіків це стає більш ефективним і наочним.
Розглянемо завдання, що ілюструє дану тезу.
При яких значеннях параметра а рівняння ![]() має рівно три корені?
має рівно три корені?
Скористаємося графіком функції ![]() , який було побудовано у першому розділі (рис. 1.6), на якому позначимо серію паралельних прямих
, який було побудовано у першому розділі (рис. 1.6), на якому позначимо серію паралельних прямих ![]() .
.
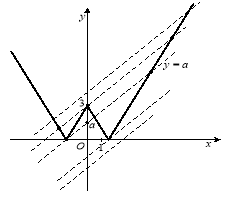 Рис. 2.1
Рис. 2.1
За допомогою графіків отримуємо відповідь: три корені дане рівняння
має при ![]() і при
і при ![]() .
.
Відповідь: 1,5: 3
2.1. Рівняння, які містять суму модулів лінійних функцій
Приклад 2.1.1. Скільки розв’язків в залежності від параметра ![]() має рівняння
має рівняння ![]() ?
?
Скористаємося графіком функції ![]() , який було побудовано у
, який було побудовано у
першому розділі (рис. 1.8), на якому позначимо серію паралельних прямих ![]() .
.
 Рис. 2.2
Рис. 2.2
За допомогою графіка (рис.2.2) проводимо дослідження.
Відповідь: 1) при ![]() рівняння коренів не має,
рівняння коренів не має,
2) при ![]() рівняння має безліч коренів (
рівняння має безліч коренів (![]() ),
),
3) при ![]() рівняння має два корені.
рівняння має два корені.
Приклад 2.1.2. Знайдіть усі значення параметра а, при яких рівняння ![]() має безліч розв’язків.
має безліч розв’язків.
Проаналізуємо певну властивість графіка функції ![]() . Відстань між точками −1 та 2 дорівнює 3, і безліч коренів рівняння має при
. Відстань між точками −1 та 2 дорівнює 3, і безліч коренів рівняння має при ![]() . Отже, для рівняння (2.1.2) або
. Отже, для рівняння (2.1.2) або ![]() , або
, або ![]() і довжина кожного з відрізків
і довжина кожного з відрізків
дорівнює 3 (як у другому пункті відповіді до попереднього прикладу). Ця умова виконується при ![]() або при
або при ![]() .
.
Відповідь: − 4; 2.
Приклад 2.1.3. При яких значеннях параметра а рівняння![]()
має корені, але жоден з них не належить інтервалу ![]() ?
?
Виконаємо певні заміни: нехай ![]() ,
, ![]() ,
, ![]() ; тоді рівняння матиме вигляд
; тоді рівняння матиме вигляд ![]() . Зазначимо, що необхідною умовою для наявності коренів цього рівняння є виконання нерівності
. Зазначимо, що необхідною умовою для наявності коренів цього рівняння є виконання нерівності ![]() , або
, або ![]() .
.
Розглянемо графік функції ![]() ; відстань між точками т та п осі абсцис дорівнює
; відстань між точками т та п осі абсцис дорівнює ![]() , отже,
, отже, ![]() і дане рівняння має безліч розв’язків:
і дане рівняння має безліч розв’язків: ![]() (як у другому пункті відповіді до прикладу 2.1.1).
(як у другому пункті відповіді до прикладу 2.1.1).
За умовою ця множина ![]() не має спільних точок з інтервалом
не має спільних точок з інтервалом ![]() , тому можливі два випадки:
, тому можливі два випадки: ![]() або
або ![]() . Отже, маємо систему:
. Отже, маємо систему:  , розв’язком якої є множина
, розв’язком якої є множина ![]() .
.
Відповідь: ![]()
2.2. Рівняння, які містять різницю модулів лінійних функцій
Приклад 2.2.1. Скільки розв’язків в залежності від параметра ![]() має рівняння
має рівняння ![]() ?
?
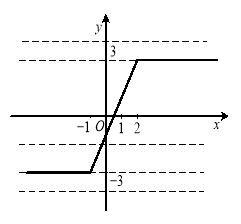 Рис. 2.3
Рис. 2.3
За допомогою графіка (рис. 2.3) проводимо дослідження.
Відповідь: 1) при ![]() рівняння коренів не має,
рівняння коренів не має,
2) при ![]() або
або ![]() рівняння має безліч коренів,
рівняння має безліч коренів,
3) при ![]() рівняння має один корінь.
рівняння має один корінь.
Приклад 2.2.2. При яком найменшому цілому значенні параметра ![]() рівняння має рівно два різних кореня:
рівняння має рівно два різних кореня: ![]() ?
?
Перетворимо дане рівняння: ![]()
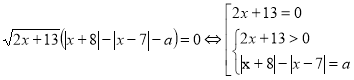 . Зауважимо, що один із коренів – це число
. Зауважимо, що один із коренів – це число ![]() . Отже, маємо знайти найменше ціле значення параметра
. Отже, маємо знайти найменше ціле значення параметра ![]() , при якому
, при якому
рівняння ![]() має єдиний корінь, що задовольняє умову
має єдиний корінь, що задовольняє умову ![]() .
.
 Рис. 2.4
Рис. 2.4
За допомогою графіка (рис. 2.4) знаходимо, що шукане значення параметра а дорівнює числу ![]() .
.
Відповідь: ![]() .
.
2.3. Застосування властивостей квадратичної функції
Приклад 2.3.1. При яких значеннях параметра а один з коренів рівняння ![]() менший за 1, а інший – більший за 1?
менший за 1, а інший – більший за 1?
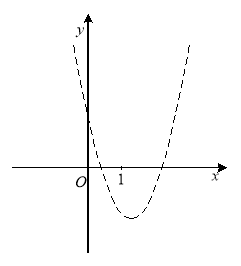 Рис. 2.5
Рис. 2.5
Розглянемо графік функції ![]() (рис. 2.5); умова
(рис. 2.5); умова ![]() виконується, якщо
виконується, якщо ![]() ;
; ![]() .
.
Відповідь: ![]() .
.
Приклад 2.3.2. При яких значеннях параметра а один з коренів рівняння ![]() менший за 1, а інший – більший за 1?
менший за 1, а інший – більший за 1?
Цей приклад є певним узагальненням попереднього. Розглянемо графік функції
![]() , який для
, який для ![]() виглядає так само, як на рисунку 2.5, а
виглядає так само, як на рисунку 2.5, а
для ![]() є симетричним йому відносно осі ох. Тому для виконання умови отримаємо дві системи:
є симетричним йому відносно осі ох. Тому для виконання умови отримаємо дві системи:
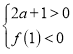 або
або 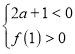 ;
; ![]() ;
; ![]() ;
;
отже, ![]() .
.
Відповідь: ![]() .
.
Приклад 2.3.3. При яких значеннях параметра а обидва корені рівняння ![]() більші за 1?
більші за 1?
 Рис. 2.6
Рис. 2.6
Розглянемо графік функції ![]() (рис. 2.6); умова
(рис. 2.6); умова ![]() виконується, якщо
виконується, якщо 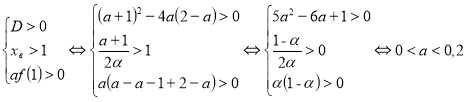 .
.
Відповідь: ![]() .
.
Приклад 2.3.4. При яких значеннях параметра а всі корені рівняння ![]() належать проміжку
належать проміжку ![]() ?
?
Розглянемо функцію ![]() ; 1) для
; 1) для ![]() маємо
маємо ![]() , коренем рівняння
, коренем рівняння ![]() є число 0,5, яке належить проміжку
є число 0,5, яке належить проміжку ![]() , отже,
, отже, ![]() задовольняє умові завдання;
задовольняє умові завдання;
2) для ![]() розглянемо графік функції
розглянемо графік функції ![]() (рис. 2.7);
(рис. 2.7);
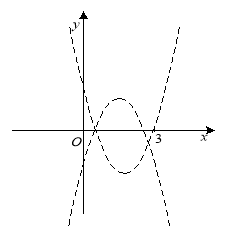 Рис. 2.7
Рис. 2.7
Виконання умови: всі корені рівняння належить проміжку ![]() приводить до системи
приводить до системи 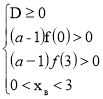 , яка рівносильна такій
, яка рівносильна такій 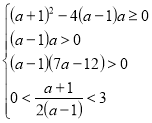 ; розв’язком якої є множина
; розв’язком якої є множина 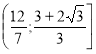 . Враховуючи перший пункт, маємо
. Враховуючи перший пункт, маємо 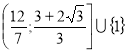
Відповідь: 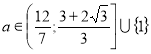 .
.
Приклад 2.3.5. Доведіть, що для будь-якого значення параметра а рівняння
![]() має дійсні корені.
має дійсні корені.
Розглянемо графік функції ![]() (рис.2.8). Зазначимо:
(рис.2.8). Зазначимо:
![]() ;
; 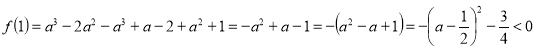 .
.
Отже, на проміжку ![]() функція змінює знак, і за теоремою Коші існує с, для якого
функція змінює знак, і за теоремою Коші існує с, для якого ![]() і с – корінь рівняння.
і с – корінь рівняння.
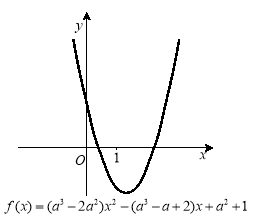
Рис.2.8
Примітка. Стандартний метод розв’язування цієї вправи передбачає складання дискримінанту даного квадратного рівняння (повний многочлен шостого степеня) та доведення його невід’ємності, що є дуже важкою справою.
2.4. Розв’язування систем з параметрами
Приклад 2.4.1. Скільки розв’язків в залежності від параметру а має система: 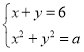
Розглянемо множину точок площини, що задають рівняння системи (рис. 2.9):
це пряма і безліч концентричних кіл з центром у точці ![]() . Коло дотикається до прямої, якщо
. Коло дотикається до прямої, якщо ![]() ;
; ![]() .
.
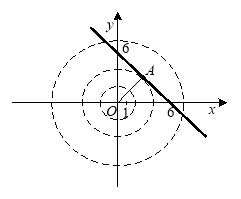 Рис. 2.9
Рис. 2.9
Відповідь: 1) якщо ![]() розв’язків немає;
розв’язків немає;
2) якщо ![]() , тоді розв’язок один;
, тоді розв’язок один;
3) якщо ![]() , тоді розв’язків два.
, тоді розв’язків два.
Приклад 2.4.2. Скільки розв’язків в залежності від параметру а має система:
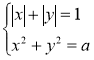 ?
?
Розглянемо множину точок площини, що задають рівняння системи (рис. 2.10):
це квадрат і безліч концентричних кіл з центром у точці ![]() .
.
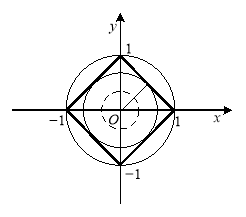 Рис. 2.10
Рис. 2.10
Коло може бути вписаним або описаним навколо квадрата, тоді маємо 4 розв’язки; коло може перетинати квадрат у 8 точках, або не мати з ним жодної спільної точки.
Відповідь: 1) якщо ![]() розв’язків немає;
розв’язків немає;
2) якщо ![]() або
або ![]() , тоді розв’язків чотири;
, тоді розв’язків чотири;
3) якщо ![]() , тоді розв’язків вісім.
, тоді розв’язків вісім.
Приклад 2.4.3. При яких значеннях параметру а система має три розв’язки: 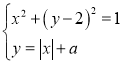
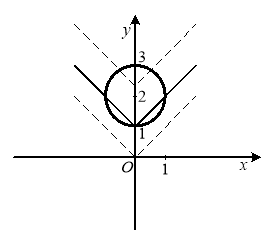 Рис. 2.11
Рис. 2.11
Розглянемо множину точок площини, що задають рівняння системи (рис. 2.11):
це коло з центром у точці ![]() , радіусом 1 і безліч ламаних, отриманих пара-
, радіусом 1 і безліч ламаних, отриманих пара-
лельним перенесенням ламаної ![]() вздовж осі Оу. Система має три розв’язки, якщо
вздовж осі Оу. Система має три розв’язки, якщо ![]() .
.
Відповідь: 1
Висновок до другого розділу
У другому розділі розглянуто завдання, які досить ефективно демонструють переваги графічного методу при розв’язуванні вправ з параметрами. Розділ місить достатню кількість вправ, до кожної з них є графічна ілюстрація.
Робота складається з двох розділів, містить вступ, висновки та список використаних джерел.
В першому розділі розглянуто основні методи побудови графіків, зокрема: за загальною схемою, за допомогою геометричних перетворень та з використанням додавання графіків на основі монотонності функцій. Надані приклади демонструють переваги використання властивостей функцій при розв’язуванні нестандартних рівнянь та рівнянь підвищеної складності.
Другий розділ присвячено завданням, які досить ефективно демонструють переваги графічного методу при розв’язуванні вправ з параметрами. Розділ місить достатню кількість вправ, до кожної з них є графічна ілюстрація.
Список використаних джерел містить 7 текстових документів та 2 Інтернет-ресурси, які сприяють розкриттю обраної теми.
Список літератури та Інтернет – ресурси
1. Захарченко Н. Параметри та графіки: навч.-метод. посіб. / Надія Захарченко, Володимир Ячменьов ; [відп. за вип. О. Лісовий]. – К. : ТОВ «Праймдрук», 2012. – 56 с.
2. Апостолова Г. В., Ясінський В. В. Перші зустрічі з параметром / Г. В. Апостолова, В. В. Ясінський. – К. : Факт, 2006. – 324 с.
3. Галицкий М. Л., Сборник задач по алгебре / М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич. – М. : Просвещение, 1992. – 271 с.
4. Горштейн П. И. Задачи с параметрами / П. И. Горштейн, В. Б.,Полонский, М. С. Якир. – К. : РИА «Текст». МП «ОКО», 1992. – 288 с.
5. Назаренко О. М. Тисяча і один приклад. Рівності і нерівності: посібник для абітурієнтів / О. М. Назаренко, Л. Д. Назаренко. – Суми : Вид-во «Слобожанщина», 1994. – 272 с.
6. Шарыгин И. Ф. Факультативный курс по математике / И. Ф. Шарыгин, В. И. Голубев. – М. : Просвещение, 1991. – 248с.
7. Харік О.Ю. Матеріали для факультативних занять, спецкурсів, гуртків. Математика 5-7. – Х.: Вид. група «Основа», 2008. – 143с.
8. Онлайн-курс «Математика. Підготовка до ЗНО»
https://prometheus.org.ua/zno/
9. Інтернет - ресурс
http://static.klasnaocinka.com.ua/uploads/editor/4795/394836/sitepage_87/files/
zaharchenko.pdf
Анотація
Цю роботу присвячено популяризації графічного методу та використання властивостей функцій для розв’язування рівнянь підвищеної складності, нестан-дартних рівнянь та вправ з параметрами.
Annotation
This article deals with the problems of solution non-standarted math equations
and exercises with parameters through graphic of functions and their properties.


про публікацію авторської розробки
Додати розробку
