Нестандартні прийоми розв'язування рівнянь

Про матеріал

Нестандартні прийоми розв'язування рівнянь до уроку математики.Нестандартні прийоми розв'язування рівнянь

Перегляд файлу

Нестандартні прийоми розв’язування рівнянь

Нестандартні прийоми розв'язування рівнянь.

Усе частіше в літературі зустрічаються рівняння, розв'язування яких стандартними способами важке, громіздке або неможливе. Тоді можна спробувати використовувати властивості функцій. Іноді такий підхід приводить до більш простого і раціонального розв'язання .

Розглянемо рівняння . Його можна розв’язати стандартним способом – зведенням до квадратного рівняння. Але не важко помітити, що друге рівняння допускає нестандартне розв’язування: його корені - очевидні. А оскільки будь – яке квадратне рівняння має не більше двох дійсних коренів, то на цьому його розв’язування закінчується.

Або звернемось до рівняння до нього теж можна застосувати згаданий прийом, попередньо додавши до обох частин рівняння 3, одержимо або . Звідси,

Отож, розглянемо такі властивості функцій, що входять в рівняння як його складові, які б привели до нестандартного їх розв’язування та продемонструємо їх практичне застосування.

Використання області визначення та області значень функцій .

. Скінченна область допустимих значень.

Якщо область допустимих значень ( ОДЗ )рівняння складається із скінченого числа значень, то для розв’язування досить перевірити всі ці значення. У тому випадку, коли ОДЗ – порожня множина ( не містить жодного числа ), ми можемо зразу дати відповідь, що задане рівняння не має коренів. Тому перед безпосереднім розв’язанням рівняння, потрібно його проаналізувати, прослідкувати за поведінкою окремих членів рівняння для допустимих значень невідомої змінної.

Наприклад, якщо потрібно розв’язати рівняння , то його ОДЗ задається системоюяка не має розв’язків.

Тобто, ОДЗ заданого рівняння не містить жодного числа, і тому це рівняння не має коренів.

Приклад 1. Розв’язати рівняння

ОДЗ:

Область допустимих значень для змінної х складається тільки з числа 2. Легко перевірити, що х = 2 – корінь рівняння.

Перевірка

Отже, х = 2 – корінь рівняння.

. Використання властивості монотонності функцій.

Вданому випадку спрацьовує така схема розв'язування: підбираємо один чи кілька коренів рівняння, доводимо, що інших коренів немає, при цьому використовуючи теореми про корені рівнянь , а саме :

Теорема 1. Якщо в рівнянні функція зростає ( спадає) на деякому проміжку, то це рівняння може мати не більш ніж один корінь на цьому проміжку.

Теорема 2. Якщо в рівнянні функція зростає на деякому проміжку, а функція спадає на цьому самому проміжку ( або навпаки ), то це рівняння може мати не більш ніж один корінь на цьому проміжку.

Справді , якщо функція монотонна, то таке рівняння має лише один корінь, бо для монотонної функції нерівним значенням аргументу відповідають нерівні значення функції. Графічно це означає, що пряма лінія, паралельна осі абсцис( графік функції - константи), не може перетинати графік монотонної функції більше, ніж в одній точці.

Якщо - кусково – монотонна функція, то рівняння може мати не тільки більш як один корінь, але навіть нескінченне їх число, коли має нескінченне число проміжків монотонності. Проте їх не може бути більше, ніж число проміжків монотонності кусково – монотонної функції.

Приклад 1. Розв'язати рівняння: .

ОДЗ:.Функція f(x) = зростаюча і коли х = 243, набуває найменшого значення (243) = 3. Функція спадна на ОДЗ і, коли х = 243, досягає найбільшого значення .

, тобто х = 243 – єдиний корінь.

Тим часом поняття монотонності функції можна використати, розглядаючи питання про рівносильність широкого класу рівнянь. Так, на практиці, щоб дістати розв’язки рівнянь, нерідко доводиться брати одну й ту саму функцію від обох частин; порівняння значень складних функції , в яких зовнішня функція одна й та сама, - замінювати порівнянням значень внутрішніх функцій, тобто виконувати перехід:, скориставшись відомою теоремою : „ Рівняння і рівносильні, якщо їх області визначення однакові, а функція монотонна. ” Проілюструємо застосування даної теореми на прикладі.

Приклад 2. Розв’язати рівняння .

Запишемо це рівняння в такому вигляді:.

Оскільки областю визначення рівняння є множина всіх дійсних чисел і зовнішня функція монотонна, то воно буде рівносильним рівнянню , корені якого .

. Використання обмеженості функції. Оцінка лівої і правої частин рівнянь.

Деякі рівняння можна розв’язати за допомогою оцінки лівої та правої частин рівняння. Даний прийом базується на такій властивості: нехай потрібно розв’язати рівняння виду f(x) = φ(x) і з’ясувалося, що то рівність між лівою і правою частинами можлива тоді і тільки тоді, коли одночасно дорівнюють а. Тобто

якщо то .

Приклад 1. Розв’язати рівняння

В даному рівнянні множина значень функції, що стоїть у лівій частині, множина невід'ємних чисел, а множина значень функції, що стоїть в правій частині, - множина не додатних чисел: = -

Тому це рівняння рівносильне системі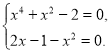

Звідси одержуємо єдиний корінь рівняння х = 1.

Аналогічно розв’язується рівняння виду

в якому всі функції - доданки невід’ємні. Очевидно, що в цьому випадку рівністьобов’язково буде виконуватись, лише коли всі функції – доданки дорівнюють нулю. Тобто , сума кількох невід’ємних функцій дорівнює нулю тоді і тільки тоді, коли всі функції одночасно дорівнюють нулю. Розглянемо приклади.

Приклад 1. Розв'язати рівняння

ОДЗ: .

Маємо: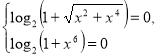

Звідси, х = 0.

Приклад 2. Розв’язати рівняння .

Задане рівняння рівносильне системі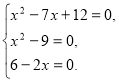

З третього рівняння одержуємо х = 3, що задовольняє і всій системі.

Отже, задане рівняння має єдиний корінь х = 3.

Приклад 3. Розв’язати рівняння .

Множина значень функції є інтервал,

а функції є інтервал .

Оскільки спільні значення відсутні , то рівняння розв’язку не має.

Використання властивостей взаємнообернених функцій.

Розглянемо такі властивості взаємнообернених функцій :

Властивість 1.Якщо та взаємнообернені функції, то їх графіки симетричні відносно прямої y = х.

Властивість 2. Якщо графіки взаємнообернених функцій та перетинаються, то точки їх перетину лежать на прямій y = х.

Властивість 3. Якщо та взаємно обернені функції, то рівняння рівносильне рівнянню або рівнянню g(x) = x.

Наприклад. Розв'язати рівняння:

Покладемо , тоді . Функції взаємно обернені. За властивістю 3, рівняння рівносильне рівнянню ; ,

Яке, у свою чергу, рівносильне рівнянню

Коренями останнього рівняння будуть числа 1, , .

Ці самі корені матиме і початкове рівняння .

Ведення параметра.

Цей спосіб полягає в тому, що сталу, яка входить до рівняння, сприймають як параметр і розв'язують рівняння відносно параметра.

Розглянемо рівняння .

Нехай .

Матимемо рівняння

Розв'яжемо його відносно а:

Один з коренів рівняння уже знайдено: х = .

Два інших знайдемо з рівняння .

Отже, розв'язками рівняння будуть числа: ; ; .

Допомагає геометрія.

Іноді доданки, що входять до складу рівняння, нагадують формули, якими записуються такі теореми, як теорема Піфагора, теорема косинусів тощо. Також часто використовується така важлива властивість скалярного добутку векторів: , (, якщо ||).

Приклад 1. Розглянемо рівняння: .

Воно не має коренів, коли х≤0, оскільки значення лівої частини рівняння не менше ніж 2, а у правої частини стоїть число більше, ніж 2. Будемо шукати корені цього рівняння на множині додатних чисел. Тоді перший доданок можна розглядати, як довжину гіпотенузи прямокутного трикутника з катетами 1 і х, а другий доданок – як довжину сторони трикутника, що лежить напроти кута з прилеглими до нього сторонами 1 і х. Побудуємо конструкцію, що відповідає лівій частині рівняння.

Нехай АО=ОВ=1, ОМ = х, =, ,

Тоді АМ= МВ = .

З нерівності трикутника випливає, що АМ+МВАВ. Рівність досягається у випадку, коли точка М належить відрізку АВ. Оскільки

АВ = , то ОМ = ОК. В рівнобедреному . Тоді в трикутнику АОК ОК=АО tg= Отже, х =

Допомагає тригонометрія.

Під час розв'язування ірраціональних рівнянь іноді зустрічаються вирази, що нагадують тригонометричні тотожності. У таких випадках ефективно працює тригонометрична підстановка.

Наприклад, у рівнянні відзначивши, що покладемо, де ;.

Отримуємо рівняння або .

Розкриваючи модуль при ;, отримаємо sin,

Виберемо лише ті значення , що задовольняють умову ;

Отже,

Обчислимо значення тригонометричних функцій за формулами:

Матимемо

, .

Про деякі тригонометричні рівняння

Дуже корисним під час розв’язування деяких тригонометричних

рівнянь частіше використовувати одиничне коло. Мова йде не тільки про рівняння

але й про рівняння виду

(1)

Ці рівняння можна розв’язати багатьма способами. Але розв’язок цього рівняння за допомогою одиничного кола –

один з способів, що дозволяє знайти відповідь усно. Кожному з рівнянь ( 1) на інтервалі задовольняє два з чотирьох чисел :що відповідають точкам одиничного кола. Ці числа знаходять усною перевіркою, потім записують загальний розв’язок. Інших розв’язків немає,так як для всякої іншої точки , відмінної від указаних , і по модулю рівні довжинам катетів трикутника, довжина гіпотенузи якого дорівнює 1, і за властивістю сторін ні одна з рівностей (1) неможливе.

Наприклад, рівнянню на проміжку задовольняють числа і 0.

Відповідь. .

За допомогою цього методу можуть бути розв’язані і більш складніші рівняння, наприклад,

де .

Застосування похідних до розв’язування рівнянь

Розглянемо декілька типів рівнянь, в яких використовуються похідні. Серед них рівняння, в яких потрібно вияснити, чи має розв’язок те чи інше рівняння. Ці рівняння зводяться до знаходження екстремальних значень функції або до знаходження їх областей значень.

Приклад 1. При якому значенні має розв’язки рівняння

Розв’язання. Область визначення даного рівняння – інтервал . Розглянемо на ній функцію f :

Тоді на інтервалі

так що 8/3 єдина критична точка функції f , яка є дотого ж точкою максимум, оскільки f (2) = 2, f (4) = , f (8/3) = . Отже, f приймає найбільше значення при х = 8/3, а найменше значення – при х = 4. Так як функція f неперервна, то її область значень є інтервал між її

найбільшим і найменшим значенням, тобто дане рівняння має розв’язок , якщо .

Відповідь.

Приклад 2. Скільки розв’язків має рівняння ?

Розв’язання. Область визначення даного рівняння – інтервал . Розглянемо на цьому інтервалі функцію f

Тоді .

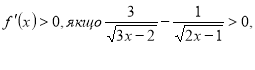
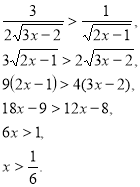
Враховуючи область визначення, маємо . Таким чином, функція f зростаюча, так що дане рівняння не може мати більше одного розв’язку.

З іншого боку, взявши будь – яке велике значення х, наприклад,

х = 200, маємо так що f як неперервна функція приймає всі значення між і , в тому числі і значення 4. Відповідь. Рівняння має лише 1 корінь.

Приклад 3. Розв’язати рівняння .

Розв’язання. ОДЗ: . Побудувавши графіки функцій і ми помітили б , що рівняння має два корені. Безпосереднім підбором і перевіркою, знаходимо , що коренями рівняння є х = 0 і х = 2. За допомогою похідної можна довести, що інших коренів немає.

Розглянемо функцію і покажемо що в неї лише одна критична точка, тобто ця функція має лише 2 інтервали ( зростання і спадання) , отже має 2 корені, які ми вже знайшли.

існує на всій області визначення()

Відповідь.

Про деякі цікаві рівняння з нескінченним числом квадратних радикалів.

В шкільному курсі алгебри і початків аналізу проходить знайомство з теоремою Вейєрштраса: якщо послідовність монотонна і обмежена, то вона має границю.

Розглянемо як дана теорема застосовується до розв’язування рівнянь з нескінченним числом квадратних коренів.

Приклад 1. Розв’язати рівняння

Піднесемо до квадрату обидві частини рівності :

Так як другий доданок співпадає з лівою частиною початкового рівняння, то

Відповідь. 42

Приклад 2. Розв’язати рівняння .

Піднесемо в квадрат обидві частини рівності, одержимо

Ще раз підносимо до квадрата

Оскільки другий доданок дорівнює 3, знайдемо

Можна також чергувати корені різного порядку. Наведемо приклади такого роду.

Приклад 3.

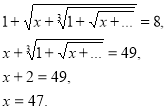
Розв’язування рівнянь, що містять змінну під знаком модуля

Для розв’язування рівнянь, що містять змінну під знаком модуля, найчастіше використовуються такі методи: за означенням модуля, піднесенням до квадрату лівої і правої частини, метод інтервалів. Але можна розв’язувати ці рівняння, використовуючи формулу відстані між двома точками координатної прямої.

Розглянемо цей прийом на прикладі

На числовій прямій потрібно знайти точки, сума відстаней яких від точок

х = - 5 і х = 8 дорівнює 16. Позначимо через у відстань, на якій знаходиться точка зліва від точки х = 5, одержимо допоміжне рівняння у + (у + 13) = 16 або у = 1,5, тобто х₁= - 6,5.

В середині інтервалу точок, що задовольняють рівняння, немає. Справа від точки х = 8 на відстані, що дорівнює 1,5, знаходиться друга точка, що задовольняє рівняння : х₂ = 9,5.

Відповідь.

Використовуючи числову пряму можна встановити, що рівняння виду , де , якщо має 2 корені, причому ці корені знаходяться поза інтервалом . Якщо рівняння має нескінченну множину коренів, причому розв’язком є інтервал . Якщо рівняння коренів немає.

Розглянемо приклади розв’язання рівнянь, що містять різницю модулів.

На числовій прямій потрібно знайти різницю відстаней яких до точок х = - 4 і х = 2 дорівнює 5. Так як відстань між точками х = - 4 і х = 2 дорівнює 6, то шукана точка знаходиться в середині інтервалу .

Позначимо через у відстань від шуканої точки до точки х = - 4, одержимо

у – ( 6 - у) = 5, або у = 5,5, тобто х = 1,5.

Відповідь.

Порівнюючи відстань між точками числової прямої, легко встановити, що рівняння виду має один розв’язок, якщо ; в цьому випадку шукана точка знаходиться внутрі інтервалу . Якщо рівняння має нескінченну множину коренів. Якщо рівняння коренів не має.

В тих випадках, коли коефіцієнти при х відмінні від 1, їх можна винести за знак модуля, а потім розв’язувати рівняння прийомом, поданим вище. Наприклад, рівняння запишемо у вигляді

На числовій прямій потрібно знайти точки, відстань яких від точки

х = 3 були в 4 рази менші, ніж від х = 5.

Нехай шукана точка знаходиться поза інтервалом зліва від точки

х = 3 на відстані у , тоді маємо рівняння 4у = у + 2, у =2/3, тобто х = .

Нехай шукана точка знаходиться внутрі інтервала на відстані z від точки 3, тоді маємо рівняння : 4z = 2 – z, звідки z = 2/5 , а х = .

Поза інтервалом справа від х = 5 рівняння коренів не має.

Відповідь.

Отже, розв’язуючи рівняння , що містять змінну під знаком модуля, вже на початковому етапі, склавши допоміжне рівняння, ми ще до розв’язання рівняння встановлюємо, в яких проміжках потрібно шукати корені і скільки коренів має рівняння.

Розглянемо ще два такі рівняння :

Приклад 1.